中央开槽箱梁断面扭转涡振全过程 气动力演化特性
刘圣源,胡传新,赵 林,2,葛耀君,2
(1. 同济大学土木工程防灾国家重点实验室,上海 200092;2. 同济大学桥梁结构抗风技术交通运输行业重点实验室,上海 200092)
随着跨度的增加,桥梁结构对风的作用更加敏感。为了提高大跨度桥梁的颤振稳定性,中央开槽箱梁近年来得到许多应用[1-3]。经过系列实际桥梁工程的试验对比与实测检验,与闭口箱梁相比,中央开槽箱梁的涡振性能仍存在深入提升气动稳定性的优化空间[4-5]。
桥梁断面存在两种不同的旋涡脱落方式,一种是断面尾部交替脱落的卡门涡[6],另一种是由附属结构产生的单剪切层分离涡[7]。通过在结构尾部安装分离板可以抑制由卡门涡所引起的涡振[8],而由分离涡所引起的涡振可通过抑流板等气动措施进行控制[9]。Li 等[10―11]通过对西堠门大桥涡振的现场实测,发现在涡振开始阶段,旋涡脱落只发生在槽内和下游箱梁尾部区域,而在涡振锁定区,涡脱扩展到整个下游箱梁下表面区域并和槽内旋涡连接到一起。基于风洞测压试验与流场显示相结合的方法能够深入研究槽宽变化和桥面附属结构对中央开槽箱梁在静止时的绕流特性、表面压力分布和振动时的涡振性能的影响[12-14]。发现随着槽宽的变化,箱梁周围流态表现出3 种模式,并伴有4 种涡振类型的变换;气流会在上游箱梁风障、检修车轨道等透风率较低的桥面附属结构处产生较大的流动分离,造成槽内上下剪切层距离增大,使得槽内旋涡无法形成,从而减弱竖向涡振,但附属结构处产生的剧烈流动分离会在下游箱梁尾流区引起大尺度的卡门涡脱,产生强烈的周期脉动升力矩,从而引发扭转涡振。上述研究表明中央开槽箱梁在整个涡振过程中气动力具有明显的演化特性,各个区域的分布气动力对涡振的贡献也不一致,但既有研究在一定程度上忽视了这些特性的量化影响。
参照《中药新药治疗腰椎问盘突出症的临床研究指导原则(草案)》制订疗效评定:①治愈:症状、体征消失,直腿抬高70°以上,恢复正常工作,能行走2 km以上。②显效:症状、体征得到改善,直腿抬高试验呈阴性,能正常工作。③好转:腰腿痛减轻,腰部活动功能改善,直腿抬高可疑阳性,部分恢复工作。④无效:治疗方案无效或需要调整治疗方案。
通过添加机械措施、附属构件或优化主梁气动外形可以显著提升桥梁的涡振性能[4,15―16]。Xu等[17-18]通过局部升力矩与总体升力矩之间的相关性研究了闭口箱梁扭转涡振过程中分布气动力对整体涡激力的贡献,解释了安装在某些位置导流板抑制涡振无效的原因,但忽略了脉动压力和相关性对贡献值的综合影响。Hu 和Zhao 等[19-20]基于同步测振、测压风洞试验分析了流线闭口箱梁断面涡振过程表面压力演化特性,通过同时考虑压力脉动及分布气动力与整体涡激力相关程度的贡献值解释了抑流板和导流板的制振机理。郭增伟等[21]通过风洞测压试验对比流线型扁平钢箱梁原断面振动、静止以及安装抑流板后表面压力系数的时域和频域统计特性揭示抑流板抑制机理,认为抑流板减弱了箱梁中下游位置压力脉动的分布强度和作用时序的相关性,可以有效地抑制涡振。
目前的中央开槽箱梁涡振研究在一定程度上忽视了涡振过程中箱梁表面周围流场和气动力演化特性及气动力的局部效应。涡振过程不同阶段结构表面的旋涡演化会引起气动力特性的变化,最终反映到涡振响应的演化,因此从涡振过程表面气动力演化特性的角度去揭示中央开槽箱梁的涡振机理十分重要。本文基于测压、测振风洞试验,针对中央开槽箱梁研究了涡振起振点、上升区中点、振幅极值点、下降区中点和涡振结束点等涡振过程不同阶段箱梁表面气动力的演化特性,并与常用闭口箱梁涡激振动特性综合比较。
1 风洞试验与涡振性能测试
1.1 风洞试验概况
研究对象为中央开槽箱梁断面,几何缩尺比采用1∶70,模型长度L=2000 mm,宽度B=514.6 mm,高度H=46.9 mm,开槽率为16.7%。试验模型由铝制框架提供整体刚度,行车道防撞栏杆采用ABS板雕刻,采用多种规格金属铜管型材制作检修道栏杆,外衣采用轻质航空木板。在模型中部无横梁断面布置测压孔,压力梯度变化剧烈位置适当加密,测点间距为8 mm~15 mm,共计84 个测点。测压管内径为1.1 mm,测压管长度为1400 mm,测压孔布置及主梁断面尺寸如图1 所示。

图1 主梁断面尺寸及测压点布置 /mm Fig.1 Geometrical dimensions of a bridge sectional model and layout of pressure taps
在图2的文本共时结构中,行动元(actant)[注]有“行动位”“角色”“行动素”“行动单位”及“行动者“等其它多种译法,指参与过程的人或作为谓语之主语的事物。之间关系的形成同本文第一部分的分析。 社会伦理的约束使得玛吉和亚当亲如夫妻的关系不能继续,玛吉与亚当处于矛盾对立关系。这一关系也是最基本的对立关系,是文本的第一推动力,后续关系皆由此衍生。同样,亚美利戈和夏洛特也因女婿与继母的关系而被社会伦理置于矛盾对立面。

表1 主梁节段模型主要参数 Table 1 Main parameters of model
位移测量采用日本 Panasonic 公司HL-C235CE-W 型激光位移传感器,测量范围350±200 mm,分辨率8 μm,线性度误差在±0.08%以内。表面压力测试使用美国PSI 公司生产的精度为±0.05%,测量分辨率为±0.003%的DTC Initium电子压力扫描器。位移信号和压力信号的采样频率为256 Hz,采样时间为60 s。
试验在同济大学TJ-2 号大气边界层风洞中进行,该风洞是一个水平布置的闭口回流式边界层风洞,试验段长15 m、宽3.0 m、高2.5 m,试验风速范围为1.0 m/s~68 m/s 连续可调,湍流度Iu≤0.5%,风速均匀性指标δU/U<1%,气流竖向和水平偏角均小于0.5°,在没有风场处理措施时接近均匀流,节段模型风洞试验概况如图2 所示。
式中:Caero-i为无量纲化后的贡献值;σi为i测点压力 根 方 差; 对 于 扭 转 涡 振bi=|sin(θi)(xi-xc)+ cos(θi)(yi-yc)|,对于竖向涡振bi=B;ρi为i测点分布气动力与涡激力的相关系数。Caero-i为正时,i测点分布气动力对涡激力起增强作用;Caero-i为负时,i测点分布气动力对涡激力起抑制作用。

图2 节段模型风洞试验概况 Fig.2 Sectional model and testing conditions
1.2 涡振响应
试验来流风速为2.0 m/s~10.0 m/s,在均匀流场环境下,中央开槽箱梁断面在+3°、0°、-3°攻角下均出现扭转涡振现象,+3°攻角下主梁断面涡振响应如图4 所示。图中,横坐标表示折算风速U*=U/ftB,其中U为来流风速,ft为扭转频率,B为节段模型宽度。涡振锁定折算风速区间为0.99~1.39,扭转最大振幅为1.58°。对应涡振起振点、上升区中点、振幅极值点、下降区中点和涡振结束点等涡振过程不同时期的典型风速,相应折算风速为0.99、1.04、1.21、1.31 和1.39,并分别对上述典型风速下箱梁表面气动力进行分析,探究涡振过程箱梁表面气动力演化特性。以下如无特别说明,均以上述风速点代替涡振不同阶段。

图3 测压管路修正频响函数 Fig.3 Frequency response transfer function

图4 节段模型扭转涡振响应 Fig.4 Torsional VIV response of sectional model
2 分布气动力演化特性
箱梁表面压力分布能够反映空气在断面周围的绕流情况,根据节段模型表面压力信号,对比分析涡振起振点、上升区中点、振幅极值点、下降区中点及涡振结束点等涡振不同阶段箱梁表面压力系数均值、压力系数根方差得到中央开槽箱梁分布气动力演化特性。
为了检验回归结果的稳健性,本文首先根据Calonico 等(2014)提出的适用于模糊断点回归带宽估计方法,估计结果如表5所示。可以发现,在IK准则下,城镇居民的教育收益率为15.2%,农村居民的教育收益率为12.1%;在CV准则下,城镇居民的教育收益率为13.7%,农村居民的教育收益率为11.4%。可以发现两种准则下的城镇居民教育收益率均大于农村居民,回归结果具有稳健性。
中央开槽箱梁整个涡振过程中,涡激力在折算风速1.04~1.34 范围内出现倍频效应,图10 给出了涡振锁定区内涡激力1 阶、2 阶谐波幅值及其比值随折算风速的变化关系。可以看出2 阶谐波幅值与1 阶谐波幅值的比值随折算风速增加呈M 型分布,在振幅极值点附近比值出现明显下降,说明涡激力的非线性程度并不随涡振振幅的增大而持续增大,两者之间无明显的线性关系。
除了《合同法》上的一般规定,对于格式条款的效力问题,《合同法》第四十条还做出了特殊规定,认定提供格式条款的一方免除其责任、加重对方责任、排除对方主要权利的,该条款无效。那变更合同成立时点的格式条款是否属于前述情形呢?

式中:Cpi(t)为i测点风压系数时程;pi(t)为i测点风压时程,压力为正,吸力为负;ρ为空气密度;Ur为来流在参考高度处的平均风速,对于均匀流场,即为来流平均风速。
1.审计委员会形式独立性研究。国内学者大多以审计委员会中独立董事的比例度量审计委员会独立性。如翟华云2006、蔡卫星等2009、柯明等2011、周国华2011、谢香兵2011、周国平等2013、刘彬2014、谢海娟等2016、陈文娟等2016、李建红2016、何卫红2016、王振秀2017等。
2.1 平均压力系数
箱梁表面平均压力系数的分布状况表征气流在模型表面的总体分布特征,能够判断气流在箱梁断面上的分离和再附情况。中央开槽箱梁涡振过程平均压力系数的空间分布演化特征如图5 所示,正负压力值以标识在模型内侧为正压、外侧为负压。为方便显示,图中未展示模型附属结构,下文中类似图示也做相同处理。可以看出仅I 区为正压区,其余测点均为负压区,平均压力在迎风侧检修车轨道附近方向突变,出现很大的吸力,说明气流在此处分离,而下游箱梁A 区、B 区平均压力系数一直保持稳定的负压,表明气流在整个绕流过程中没有在下游箱梁上表面发生明显的再附现象。另外,在整个涡振过程中,箱梁表面平均压力系数的空间分布保持稳定。

图5 涡振过程平均压力系数 Fig.5 Mean pressure coefficient distribution during VIVs
2.2 脉动压力系数
箱梁表面压力系数根方差能够反映断面上压力脉动强弱,压力系数根方差又称为脉动压力系数,图6 给出了涡振过程箱梁表面脉动压力系数空间分布演化特征,脉动压力系数标识在模型外侧。涡振刚发生时,模型运动幅值较小,此时箱梁表面压力脉动分布均匀且脉动压力系数较小;进入涡振锁定区后,A 区10#~13#测点、D 区28#~35#测点、E 区36~38#测点、H 区57#~59#测点脉动压力系数迅速增大;而涡振结束后,压力脉动又迅速减弱,基本处于分布均匀状态,类似于涡振起振时的情况。整个涡振过程中,D 区28#~35#测点、E 区36#~ 38#测点脉动压力系数演化特性最为明显,这是由于气流与模型振动之间产生强烈的耦合作用,上游脱落的旋涡在开槽处与下游箱梁发生撞击,从而造成这些测点附近压力系数脉动较大,然而Hu 和Zhao 等[19-20]的研究表明,仅以压力脉动大小并不能判断出涡振的主导区域。
图6 涡振过程脉动压力系数 Fig.6 RMS distribution of fluctuating pressure coefficients during VIVs
3 涡激力演化特性
3.1 涡激力幅频特性
相关系数的取值范围为-1~1,ρi=-1,分布气动力与涡激力反相相关;ρi=0,分布气动力与涡激力不相关;ρi=1,分布气动力与涡激力同相相关。涡振过程不同阶段箱梁分布气动力与涡激力的相关系数如图12 所示,其值以标识在模型外侧为正、内侧为负。

式中:CM(t)为无量纲升力矩;M(t)为每延米涡激力;Ue为振幅极值点处风速;n为测点总数;δi为测点每延米所占权重面积;θi为i测点压力与水平轴之间的夹角,按顺时针方向在0~2π 之间变化;xi、yi为测压点坐标;xc、yc为扭转中心坐标。
图7 给出了振幅极值点风速下的涡激力时程,可知涡激力并非单频的正弦曲线,且幅值有一定的波动。涡激力时程多频且幅值变化的现象可从图8涡激力幅值谱中进一步探讨。从图中可知,涡激力除存在卓越频率7.7Hz 外,还存在频率为15.4Hz的2 次谐波分量,倍频现象的出现反映出涡激力的非线性特性。
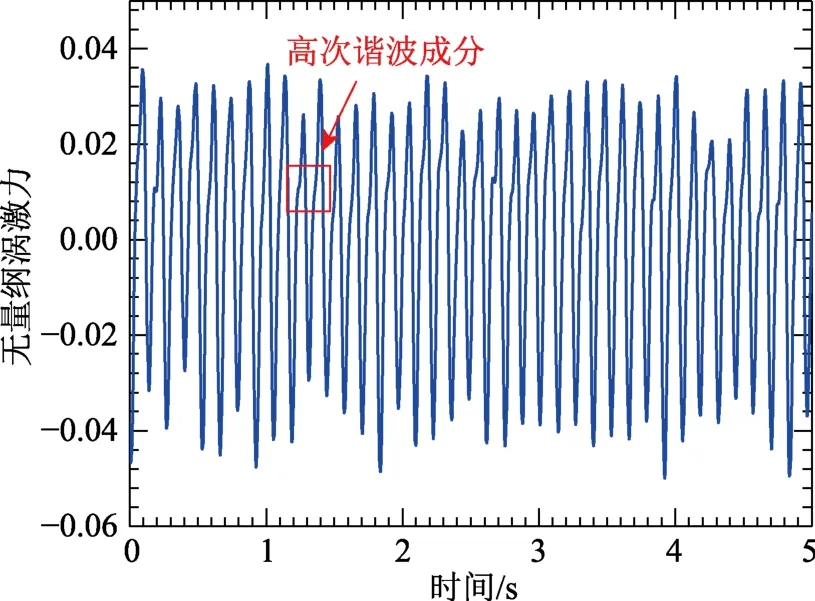
图7 振幅极值点涡激力时程(U*=1.21) Fig.7 Time history of VEF at amplitude extreme point (U*=1.21)

图8 振幅极值点涡激力幅值谱(U*=1.21) Fig.8 Amplitude spectrum of VEF at amplitude extreme point (U*=1.21)
为得到涡激力在整个涡振过程中的幅频演化特性,不同阶段涡激力幅值谱如图9 所示。可知在涡振起振点处,幅值谱比较紊乱,无明显卓越频率, 表现出宽频特性。在涡振锁定区间内,涡激力受结构运动状态控制,涡激力卓越频率与结构运动频率一致,但是锁定区间内的涡激力出现明显的高次谐波成分。在上升区中点,2 阶谐波与1 阶谐波比例为12.5%;振幅极值点涡激力幅值谱分布特性与上升区类似,但卓越频率处涡激力幅值和2 次谐波成分都明显增大,其中2 阶谐波与1 阶谐波的比例为29.1%;下降区中点涡激力幅值谱卓越频率处涡激力幅值和2 次谐波成分与振幅极值点相比都明显减小,尤其是2 阶谐波与1 阶谐波的比例更是降至4.6%,涡激力非线性程度减弱。在涡振结束点处,涡激力幅值谱仍表现出宽频特性。
测点风压系数定义为测点风压与来流动压之比,即:
根据《哮喘症状控制的标准》判定治疗效果,完全控制:患者夜间无发作、症状及活动受限,白天有症状或应用缓解药物≦1次/周,FEV 1超过80%或正常;部分控制:患者夜间偶有发作、症状或活动受限,但明显减轻,白天有症状或应用缓解药物≦2~3次/周,FEV1提升15%以上。未控制:患者临床症状及发作次数无变化甚至加重[7]。治疗有效率=(完全控制+部分控制)/总例数×100%。
一任任东家如同走马灯,旧调重弹的背后是新人不再年轻,昔年盛誉篮坛的“山东青年军”已然老去,他们在黄金年龄没有匹配上一家有着足够耐心、足够专注的俱乐部,夺冠的梦想渐行渐远,山东男篮的商业品牌价值也在这一轮轮折腾中逐渐式微。
3.2 分布气动力功率谱
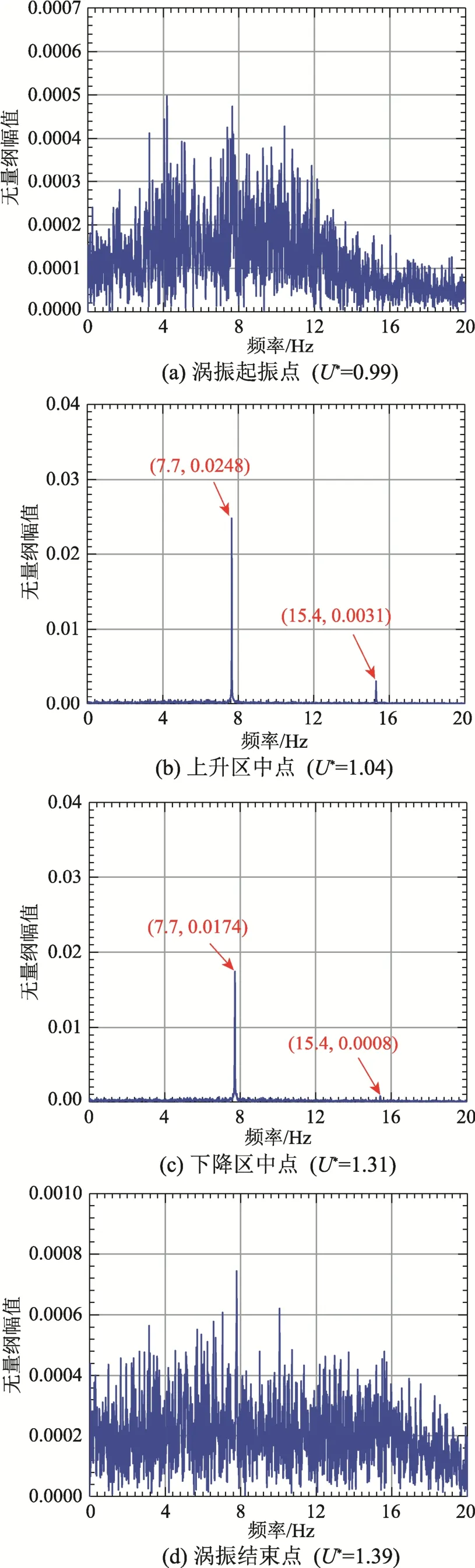
图9 涡振过程不同阶段涡激力幅值谱 Fig.9 Amplitude spectra of VEFs during VIVs

图10 锁定区内前两阶幅值比 Fig.10 Amplitude ratios between first two orders in lock-in region
分布气动力功率谱能够反映其频率特性。图11给出了涡振过程不同阶段箱梁表面分布气动力功率谱的卓越频率。在涡振起振点及结束点处,卓越频率很分散,没有固定值,说明各测点压力脉动相关性较差,各点压力脉动不同步,旋涡没有固定的脱落频率,但这两阶段均有部分测点的卓越频率接近结构扭转固有频率。在涡振锁定区间内,分布气 动力卓越频率几乎均为7.7 Hz,与结构扭转自振频率相同,各测点具有相同的压力脉动周期,旋涡具有相同的产生及脱落频率,从而导致了涡振的发生。注意到,箱梁在振幅极值点时,下游箱梁C 区18#~22#测点区域的卓越频率为15.4 Hz,两倍于结构扭转自振频率,这是由于上游脱落的旋涡与下游箱梁检修车轨道后方的旋涡在此处发生交汇,从而造成此处卓越频率出现倍频效应,这也是涡振锁定区间内涡激力出现高次谐波的原因之一。
图13 给出了涡振过程不同阶段箱梁表面分布气动力对涡激力贡献值的空间分布,正负贡献值以标识在模型外侧为正、内侧为负。A 区下游、B 区、D 区下游、G 区上游区域气动力对涡激力主要起增强作用,而H 区前端区域气动力对涡激力主要起抑制作用。因而,这些区域的分布气动力与涡振产生密切相关。通过对比图6 和图12,发现上述区域分布气动力脉动明显,分布气动力与涡激力相关性较强(A 区与B 区8#~17#测点、D 区28#~30#测点、G 区55#~56#测点相关系数均大于0.8,H 区59#测点相关系数小于-0.8)。注意到,在涡振过程中D 区上游,E 区斜腹板附近压力脉动十分剧烈,但该区域分布气动力对涡激力的贡献却十分有限,该区域测点与扭转中心间距较小及分布气动力与涡激力的相关性较差(D 区与E 区33#~38#测点相关系数绝对值小于0.5)是主要原因。同理,尽管G区下游区域46#~54#测点处分布气动力与涡激力相关性较强,但气动力压力脉动较小,最终使得贡献值较小。注意到,虽然开槽处分布气动力对涡激力的贡献值接近为0,但开槽使得上下表面空气连通,从而增加了下游箱梁上下表面气动力的相关性。中央开槽箱梁在整个涡振过程中,分布气动力对涡激力的贡献具有明显的演化特性。在涡振起振点与结束点,压力脉动较弱,分布气动力与涡激力相关性较差,整个箱梁表面对涡激力的贡献较小,贡献值几乎都在0 附近;在涡振锁定区间内,分布气动力对涡激力的贡献与涡振振幅有明显的相关性。

图11 分布气动力功率谱卓越频率 Fig.11 Predominant frequencies of aerodynamic power spectra for various pressure taps
4 分布气动力与涡激力关系
4.1 分布气动力与涡激力相关系数
分布气动力与涡激力的相关关系可以反映两者之间的相关程度和相关方向,可表达为[19-20]:

式中:ρi为i测点分布气动力与涡激力的相关系数;D(M)和D(mi)分别为扭转涡激力和分布气动力的方 差;Cov(M,mi)为扭转涡激力与分布气动力的协方差。
中央开槽箱梁表面各测点所受气动力是指各测点压力与其所占权重面积的乘积,将模型振动过程中测量的箱梁表面各点升力矩进行积分并减去均值,换算到风轴整体坐标系下,即可得到作用在模型上的涡激力,经无量纲化后可表示为:

图12 涡振过程分布气动力与涡激力的相关系数 Fig.12 Correlation coefficients between distributed aerodynamics and VEF during VIVs
整个涡振过程中A 区、B 区、D 区分布气动力与涡激力均为正相关,H 区、J 区表面几乎全为负 相关,其余区域在涡振过程不同阶段相关性出现方向变化。下游箱梁上表面A 区和下表面D 区相关系数均为正值,表明上下表面气动升力矩脉动方向一致,使得涡振振幅进一步加大。整个涡振过程中,箱梁中央开槽处F 区和L 区分布气动力与涡激力的相关性总是相反,且都在槽深一半处(F 区39#~40#测点,L 区81#~82#测点)发生方向的转变,说明气流在箱梁扭转过程中从槽内穿过,增大了槽内对角点之间的相关性。涡振起振点与结束点箱梁各个区域分布气动力与涡激力之间的相关系数均在0 附近,分布气动力对涡激力几乎没有贡献,涡振振幅较小。进入涡振锁定区后A 区下游、B 区、D 区下游、G 区等区域相关系数迅速增大(正),H 区58#、59#测点相关系数迅速减小(负),表明这些区域测点气动力在整个涡振过程中演化特性明显,有可能是引起涡振发生的主要区域,下文将通过分布气动力对涡激力的贡献对这些区域进行甄别,从而找出影响中央开槽箱梁涡振的原因。
节段模型安装在内置于风洞的端墙系统上,保证模型端部与端墙内壁间隙足够小且在试验中不会发生接触,以避免三维绕流效应。节段模型两端与吊臂相连,吊臂通过上下各4 根弹簧与端墙连接,形成弹簧悬挂系统,同时在两根吊臂两侧对称布置一个激光位移传感器。节段模型的主要参数如表1所示。
4.2 分布气动力对涡激力贡献
分布气动力对涡激力的贡献同时取决于测点压力脉动大小和分布气动力与涡激力的相关性,故箱梁表面分布气动力对涡激力的贡献值可表达为:

较长的测压管路会降低管路系统的固有频率,使压力信号中的高频成分发生显著衰减。图3 为1400 mm 长测压管的频响函数,可知低频处试验采用的测压管路系统对系统频响特性影响较小。
采收可以用铁锨从垄的边缘入铲、将薯块挖出,也可以用机器从垄的一端入铲,随着挖收铲的向前移动,薯块就会被从土壤中翻出来了,然后再人工拾捡,收获时尽量避免损伤块茎并防止块茎大量遗漏在土中。
拈花湾禅意小镇的开发注重文化推广,为举办国家级或者世界性的大型活动创造了条件。通过铁人三项赛、万人瑜伽节、世界佛教论坛等活动,对整个马山太湖国际旅游度假区的建设产生了重要影响。不断提高的配套住宿体量,使无锡过夜游客的数量逐步增长,带动了无锡2日游、3日游等旅游产品的发展,提升了无锡的旅游目的地形象。

图13 涡振过程贡献值分布特性 Fig.13 Distribution characteristics of contribution values during VIVs
中央开槽箱梁与流线型闭口箱梁涡振过程分布气动力对涡激力的贡献有显著差异,参考Hu[19]流线型闭口箱梁分布气动力对涡激力的贡献值如图14 所示,正负贡献值以标识在模型外侧为正、内侧为负。闭口箱梁在涡振前后分布气动力对涡激力的贡献较小,这与开槽箱梁在涡振起振点和涡振结束点的结果类似。进入涡振锁定区后,两种断面部分测点对涡激力的贡献明显增大。闭口箱梁A 区下游分布气动力对涡激力起增强作用,而C 区与D区转角处起抑制作用,说明上下表面气动力反相相关,增大了上下表面气动力相互抵消的程度,使得整体涡激力减小;开槽箱梁下游箱梁上下表面分布气动力对涡激力均起增强作用,说明上下表面气动力同相相关,两者的叠加增大了整体涡激力。下游箱梁上下表面对涡激力的增强作用是开槽箱梁涡振性能弱于闭口箱梁的重要原因。

图14 流线型闭口箱梁涡振过程贡献值 Fig.14 Contribution values of streamlined closed-box girder during VIVs
为进一步揭示分布气动力对涡激力贡献值与涡振振幅之间的演化关系,选取28#、59#测点作为D 区下游和H 区前端的典型测点进行分析,如图15 所示。对涡激力起增强作用的28#测点和起抑制作用的59#测点对涡激力贡献的变化规律一致,均在涡振振幅极值点处达到极值,并且这些区域分布气动力对涡激力的贡献与涡振振幅呈正相关关系。

图15 涡振过程测点气动力对涡激力贡献与振幅关系 Fig.15 Contribution values of distributed aerodynamics at typical pressure taps and torsional amplitudes during VIVs
5 结论
利用风洞测压、测振试验,研究了中央开槽箱梁断面的涡振性能,分析了该断面在扭转涡振过程不同阶段的气动力特性,从中央开槽箱梁表面分布压力与整体涡激力演化特性及分布气动力与整体涡激力的关系等方面分析了涡振过程中气动力的发展变化规律,基于分布气动力脉动强度及其与整体气动力相关性组合的思路,突出强调了开槽箱梁表面气动力对涡振效应贡献率的影响,量化了涡振发生过程有效的气动力致振机理。主要结论如下:
(1) 气动力特性与涡振振幅有明显的同步演化关系,分布气动力对涡激力的贡献与涡振振幅呈正相关关系,均在涡振锁定区间振幅极值点达到最大值。涡振锁定区内,涡激力2 次谐波成分随涡振振幅显著变化,在上升区和下降区分别总体呈现同步递增和递减变化。
(2) 箱梁表面分布气动力对整体涡激力的贡献大小取决于测点压力脉动值及分布气动力与涡激力的相关性。在涡振起振点和终止点,分布气动力对涡激力贡献较小;涡振锁定区间内,下游箱梁上下表面后部区域对涡激力起增强作用,上游箱梁上表面前部区域对涡激力起抑制作用,这些区域的气动力是引起中央开槽箱梁扭转涡振的主要原因。
李波:红土地的景区萎缩。原因主要有三方面:一个是退耕还林还草,一大部分地区消失了;第二个原因是土地撂荒;第三个原因是乱挖乱建。2010年左右这种变化开始明显,到2015年左右,红土地的摄影旅游到了一个鼎盛期,之后就慢慢衰退了。
(3) 流线型闭口箱梁上下表面下游分布气动力对整体涡激力的贡献相互抵消,而中央开槽下游箱梁上下表面对涡激力均起增强作用,这是中央开槽箱梁涡振效应强于闭口箱梁的重要原因。

