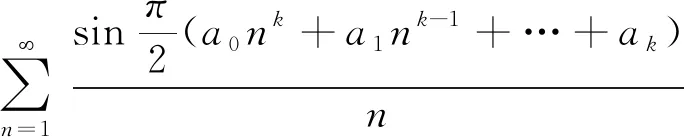一些正弦函数级数的敛散性

杜先云，任秋道

(1.成都信息工程大学应用数学学院，四川成都 610225；2.绵阳师范学院数学与物理学院，四川绵阳 621000)

1 引入

目前《高等数学》[1]与《数学分析》[2]教材中，对任意项级数收敛的内容涉及少，而大量级数的敛散需要确定.我们通过数列收敛方法来判定级数收敛.从新的角度去认识收敛数列的渐进性：当n无限增大时，可以认为收敛数列{yn}相邻两项的差所构成的数列{yn-yn-1}(n>2)，无限接近一个公差为0的等差数列，从而给出了利用yn-yn-1趋于0来判断数列收敛的方法[3].这说明了收敛数列各项变化的微小性.本文给出了任意项级数收敛的一个判定理，讨论了一些正弦级数的敛散性.

2 任意项级数收敛的判定

引理[1]设{yn}为一个有界数列.∀ε>0，∃N∈Z+，当n>N时，不等式

|yn-yn-1|<ε

恒成立，则数列{yn}收敛.

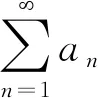
一个收敛级数任意加括号后所成级数仍然收敛，其逆命题不成立[2，3].但是有下面的定理：

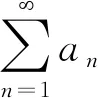
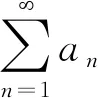
(a1+a2+…+an1)+(an1+1+an1+2+…+an2)+…+(ank+1+ank+2+…+ank)+…,

M=max{nk+1-nk|k=1,2,3,…}<.

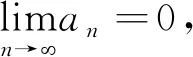
|Sn|=|bn1+bn2+…+bnk0+(ank0+1+ank0+2+…+an)|

|t|+2.

从而该级数有界.利用引理的推论可得结论.证毕.

注该定理推广了交错级数收敛的莱布尼兹定理.

3 正弦函数级数的敛散性

在[1]中，可获得：

(1)如果0<α1，a≠2kπ，k∈Z，则级数和收敛.

(2) 设有界函数f(n)满足f(n)≥0(f(n)0).如果0<α1，则级数收敛，当(a-2kπ)2+(b-2lπ)2>0,k,l∈Z时，也收敛.

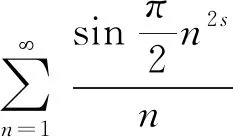
证明当s=0时，结论显然成立.当s>0时，设m∈N.根据二项式定理可得，

(4m±1)2s=(4m)2s±C12s(4m)2s-1+C22s(4m)2s-2±…±4mC2s-12s+1.

从而设(4m+1)2s≜4tm+1，(4m-1)2s≜4tm′+1，其中tm,tm′∈N.由此可得，该级数部分和

由此可得，Sn→(n→).根据级数发散的定义，该级数发散.证毕.

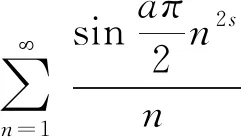
推论2设ki∈N,i=0,1,…,t，C={ai|ai∈Z,i=0,1,…,t},D={aj|aj=2rj+1∈C,rj∈Z}.

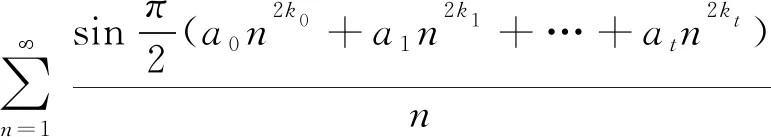
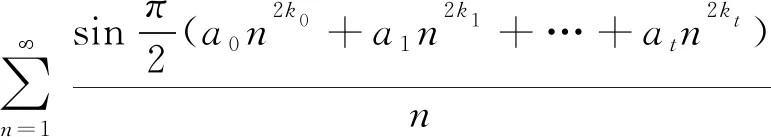
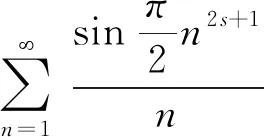
证明设m∈N.可知，设(4m+1)2s+1≜4tm+1，(4m-1)2s+1≜4tm′-1，其中tm,tm′∈N.由此可得，

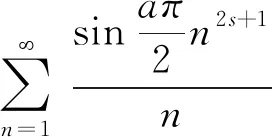
定理4设C={ai|ai∈Z,i=0,1,…,k},D={a2j|a2j=2r2j+1∈C,r2j∈Z}，

E={a2j+1|a2j+1=2r2j+1+1∈C,r2j+1∈Z}.如果|D|=2p+1，|E|=2q,p,q∈Z,则级数

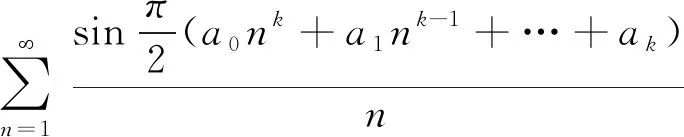
证明根据定理3、4的证明知道，当m∈N时，有

(4m+1)i=4um(i)+1,其中um(i)∈N,i=1,2,…,k；对于k=2s,s∈N时，

(4m-1)2j-1=4vm(2j-1)-1,(4m-1)2j=4vm(2j)+1,其中vm(2j-1),vm(2j)∈N,j=1,2,…,s.为了方便，设f(n)=a0n2s+a1n2s-1+…+a2s，A=a0+a2+…+a2s，B=a1+a3+…+a2s-1.因此，

f(4m+1)=[(a2s+a2s-2n2+…+a0n2s)+(a2s-1n+a2s-3n3+…+a1n2s-1)]|4m+1

=4[a2sum(0)+a2s-2um(2)+…+a0um(2s)+a2s-1u(1)+a2s-3u(3)+…

+a1u(2s-1)]+(a0+a2+…+a2s)+(a1+a3+…+a2s-1)≜4r+A+B.

根据已知条件，(i)A=4p′+1,，B=4q′,p′,q′∈Z，可得f(4m+1)=4w+1,w∈Z.

同理f(4m+3)=4r′+A-B=4w′+1,w′∈Z.可得该级数部分和

由此可得，Sn→(n→).该级数发散.对于(ii)A=4p′+1，B=4q′+2,p′,q′∈Z；(iii)A=4p′+3，

B=4q′,p′,q′∈Z；(iv)A=4p′+3，B=4q′+2,p′,q′∈Z.该级数均发散.对其它情况，类似方法可得该级数收敛.对于k=2s+1,s∈N时，类似可得结论.证毕.

推论设C={ai|ai∈Z,i=0,1,…,k},D={a2j|a2j=2r2j+1∈C,r2j∈Z}，