H2在AlnCum(n=4-6，m=1-3)团簇上的分子吸附理论研究

杨慧慧，陈雨欣，刘思含，苏 帅

(西安航空学院 理学院，西安 710077)

0 引言

人类社会的发展进步与能源息息相关，能源是一个国家发展战略的核心组成部分。目前，支持国民经济发展的主要能源还是不可再生的煤炭、石油等化石燃料。人类不断增长的能源需求和能源供给之间的矛盾日益突出，能源危机问题日益凸显。另一方面，化石燃料的使用引起的环境问题也不容小觑，环境保护关系到人类的可持续发展，人类在解决能源的危机同时要兼顾环境保护，需要开发出储量丰富、清洁、可再生的新能源，这将是人类面临的一个重大挑战。氢能是一种清洁可再生的理想能源，可从水或碳水化合物中制取，燃烧后的产物仍是水，无污染且可循环利用，而且氢燃烧所释放的热量是同质量汽油燃烧所释放热量的3倍。氢能作为化石能源的理想替代者之一，目前一直没有得到广泛应用，安全高效的储氢技术是制约氢能应用的一个关键问题。

传统的储氢方式有高压气态储氢(35-70MPa，室温)和低温液态储氢(0.1-1MPa，-253℃)，但这两种储氢方式成本较高，且存在安全隐患。无论是从储存密度还是经济效益和安全性考虑，固体储氢都被认为是最理想的储存方式。固体储氢大致可分为物理吸附储存和化学吸附储存。物理吸附储存中，氢分子吸附在多孔材料的表面或间隙中，氢分子与主体材料之间形成弱的范德瓦尔斯作用，氢分子的吸附强度较弱。化学吸附储存中，氢分子首先发生解离，然后以化学键的形式与主体材料相结合，氢气释放时需要破坏强的化学键，需要在高温环境下进行脱附，而且吸附的氢不能完全被脱附。储氢技术的研究虽然已取得了很大进步，但目前还没有一种材料可以同时具有高的储存密度、良好的热力学性能以及适宜的储放动力学性能。系统和全面的研究氢分子与材料之间的相互作用，对于寻找性能良好的储氢材料具有重要意义。

团簇研究是近些年发展起来的材料科学的新兴分支，它拥有一系列不同于块体材料的奇特性质，已被广泛应用于信息工程、材料工程、生物医药等领域，关于团簇作为储氢材料的研究非常多。铝作为一种廉价的轻质材料，铝团簇及掺杂铝团簇储氢的研究也引起了人们的广泛关注。Upton[1]等人研究了Aln(n=2-6)和H2分子的相互作用；Wang[2]等人利用光电子能谱研究了阴离子团簇Aln(n=3,6-15)与D2分子的反应；Pino[3]等人利用密度泛函理论研究了H2分子在Aln(n=2-6)团簇上的解离过程。我们之前研究了H2分子在Al6C团簇上的吸附和解离，得到H2分子在Al6C上的解离能垒仅为0.30 eV[4]。杨传路老师团队研究了H2分子在Al6Si和Al6N团簇上的吸附与解离，他们给出H2分子在Al6Si团簇上沿不同路径的解离能垒范围是0.48-1.15 eV，在Al6N团簇上沿不同路径的解离能垒范围是0.62-1.13eV[5-6]。文献[4-6]的研究表明：氢分子在Al6C、Al6Si和Al6N团簇上的分子吸附都很弱。本文中我们采用遗传算法，结合密度泛函搜索了原子Cu掺杂的AlnCum(n=4-6，m=1-3)团簇的稳定结构，分析了团簇的稳定性，研究了H2分子在团簇上的分子吸附。

1 计算方法

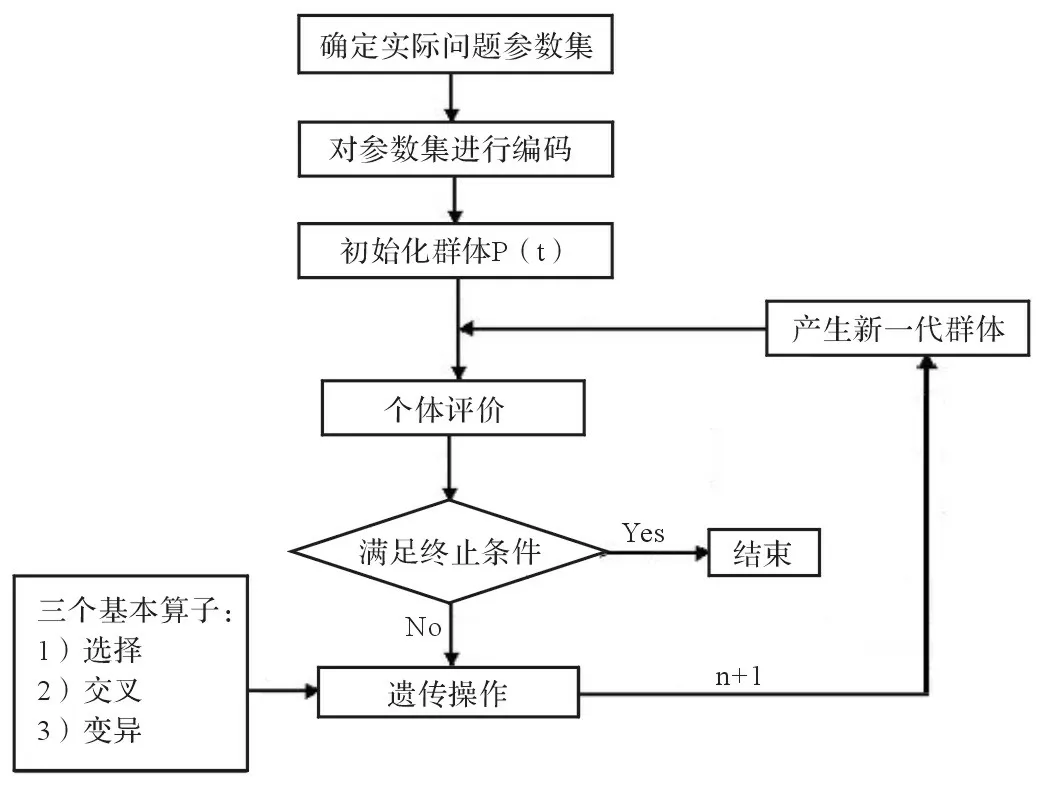
首先采用遗传算法(GA)，结合密度泛函理论(DFT)搜索了AlnCum(n=4-6，m=1-3)团簇的异构体[7-9]。对每一个团簇，遗传算法首先随机产生16个结构，接着执行遗传算符，我们选择的遗传算符有杂交、变异和交换，每个算符的几率分别为50%、30%和20%。杂交算符指从种群中选取两个个体作为父代团簇，通过切割和拼接产生子代团簇；变异算符指在种群中选取一个个体，将选定个体中的一个或多个原子的位置进行微小的变动；交换算符指将选定个体中的不同类型的原子的位置进行交换。遗传算法见图1所示。产生的子代团簇再采用密度泛函理论进行全优化，选用PBE[10]方法和加入d 极化的双数值DND 基组，使用的程序是DMol3[11-12]。每个团簇体系遗传算法的迭代次数设为2000代。遗传算法结合密度泛函理论搜索的异构体，我们又采用B3LYP方法和加入极化以及弥散函数的双ζ 6-31+G(d)、三ζ 6-311+G(d)基组进行了再优化。氢分子在团簇上的分子吸附的计算采用的方法是B3LYP/6-31+G(d,p)，计算采用Gaussian09程序执行[13]。

2 结果讨论

2.1 AlnCum(n=4-6，m=1-3)团簇的几何结构

图2给出了团簇的最稳定结构。结构Al4Cu具有C2v对称性，其构型为Cu为顶点的四棱锥结构；Al4Cu2相当于在Al4Cu团簇的一个Al-Al键上连接一个Cu原子，结构具有Cs对称性；Al4Cu3的最稳定结构具有C2v对称性，其中四个Al和两个Cu原子构成一个四棱双锥，剩余的一个Cu原子连接在Al-Al键上。

结构Al5Cu具有Cs对称性，其中三个Al和一个Cu原子构成一个四边形，另外两个Al原子位于四边形的上方。Al5Cu2具有Cs对称性，其结构与Al4Cu3类似，其中四个Al和两个Cu原子构成一个四棱双锥，剩余的一个Al原子连接在一个Al2Cu面上。Al5Cu3结构中五个Al和一个Cu构成畸变的三棱柱，剩余的两个Cu原子连接在三棱柱的两个侧面。

Al6Cu团簇的最稳定结构是在Al6四棱双锥的一个面上覆盖一个Cu原子，结构具有Cs对称性；Al6Cu2结构是在Al6三棱柱的两个侧面覆盖两个Cu原子，具有C2v对称性；Al6Cu3-a结构是在Al5Cu三棱柱的三个侧面覆盖一个Al和两个Cu原子，具有Cs对称性。

我们优化得到的Al4Cu结构与文献[14]报道的结构一致，Al5Cu结构比文献[14]报道的结构更稳定，Al6Cu结构与文献[14]报道的结构一致，比文献[15]报道的结构更稳定。据我们了解，目前没有关于掺杂多个Cu原子稳定结构的相关报道，我们首次搜索给出了掺杂2个和3个Cu原子的Al-Cu团簇的稳定结构。几何结构优化发现，掺杂多个Cu原子时，Cu原子不会在团簇表面发生聚集，而是分散的位于团簇表面。

2.2 AlnCum(n=4-6，m=1-3)团簇的结合能

团簇的结合能是衡量团簇稳定性的一个重要指标，其定义为团簇的能量与组成团簇的原子的能量之间的差值。AlnCum(n=4-6，m=1-3)团簇的结合能可用下式计算：

Eb(A1nCum)=E(A1nCum)-nE(A1)-mE(Cu)

式中，E(AlnCum)、E(Al)、E(Cu)分别是AlnCum团簇，铝(Al2P)和铜(Cu2S)的总能量。表1给出了B3LYP方法两种不同基组6-31+G(d)、6-311+G(d)计算的团簇的结合能和对称性。从表1可看出采用不同基组计算的团簇的结合能非常一致，基组6-311+G(d)比6-31+G(d)计算的结合能略高。

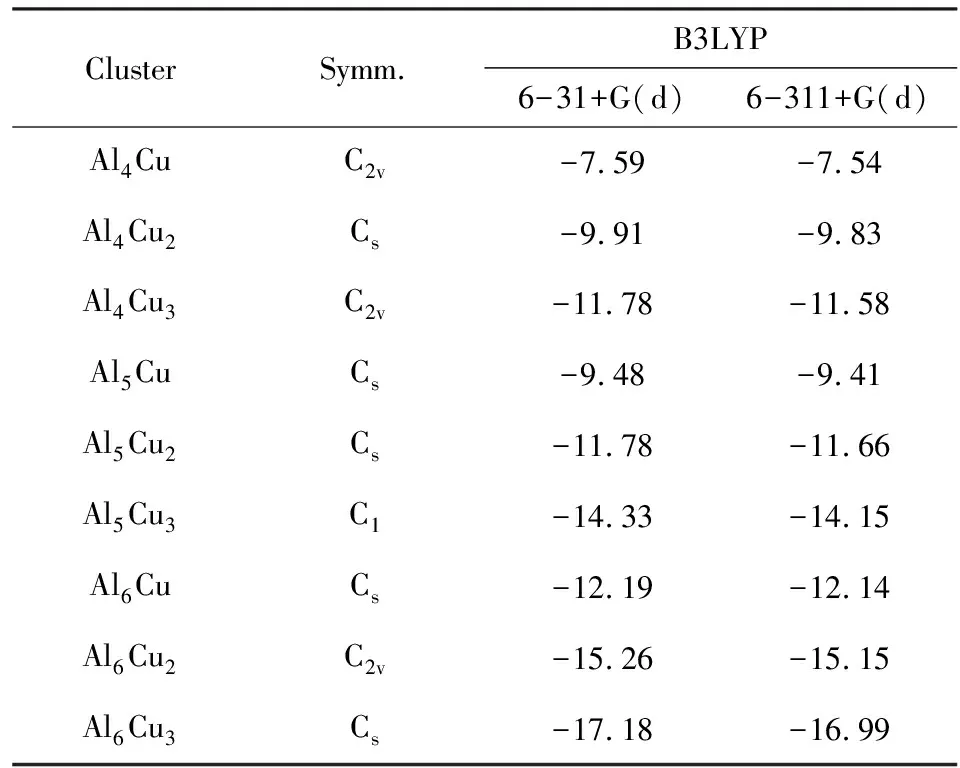
表1 不同方法计算的AlnCum(n=4-6，m=1-3)团簇的结合能 (eV)

为了讨论团簇的稳定性，我们描绘了团簇平均结合能随团簇尺寸的变化图，见图3所示。团簇的平均结合能可用下式计算：

随着团簇尺寸增大，平均每个原子参与形成的化学键增多，团簇的平均结合能增强。为了讨论掺杂Cu原子对Al团簇的稳定性的影响，我们还计算了Aln(n=4-6)团簇的结合能，其平均结合能也在图3中给出。Al7团簇价电子数目为21，在幻数20附近，具有较强的稳定性。从图3中也可看出，总原子数目为7时，掺杂Cu原子使团簇的稳定性减弱。除总原子数目为7外，Al-Cu团簇的稳定性与对应的纯Al团簇的稳定性相当或更强。

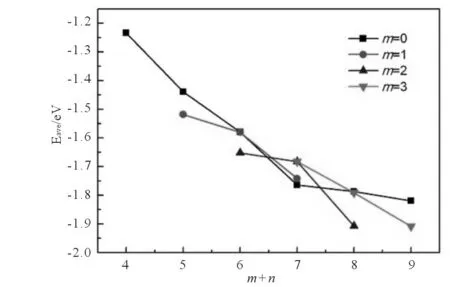
图3团簇平均结合能随总原子数目变化图

2.3 H2分子在AlnCum(n=4-6，m=1-3)团簇上的分子吸附

考虑团簇的所有不等价位(顶位、桥位和面位)和氢分子的不同取向(平行和垂直)，每个团簇体系，我们设计了10个以上的氢分子吸附结构，对所有初始结构采用B3LYP/6-31+G(d,p)进行全优化，稳定的吸附结构见图4所示。H2的吸附能和H到团簇的距离在表2中列出。吸附能用下式计算：

Eadsor=E(A1nCumH2)-E(H2)

图4给出了氢分子在AlnCum(n=4-6，m=1-3)团簇上的吸附结构。从图4可看出，氢分子倾向于以平行取向吸附在Cu原子的顶位。理想的固体储氢材料中，每个氢分子的吸附能在-0.1～-0.3 eV。从表2可看出，氢分子在Al原子的顶位的吸附强度很弱；氢分子在Cu的顶位的吸附较强，尤其是吸附结构Al5Cu-a、Al5Cu2-a、Al5Cu3-a和Al5Cu3-b中，氢分子的吸附能范围在-0.124～-0.212 eV，达到了理想的吸附强度。这明显比氢分子在纯Al团簇、Al-C团簇和Al-Si团簇上的吸附强度更大[4-5,16]。

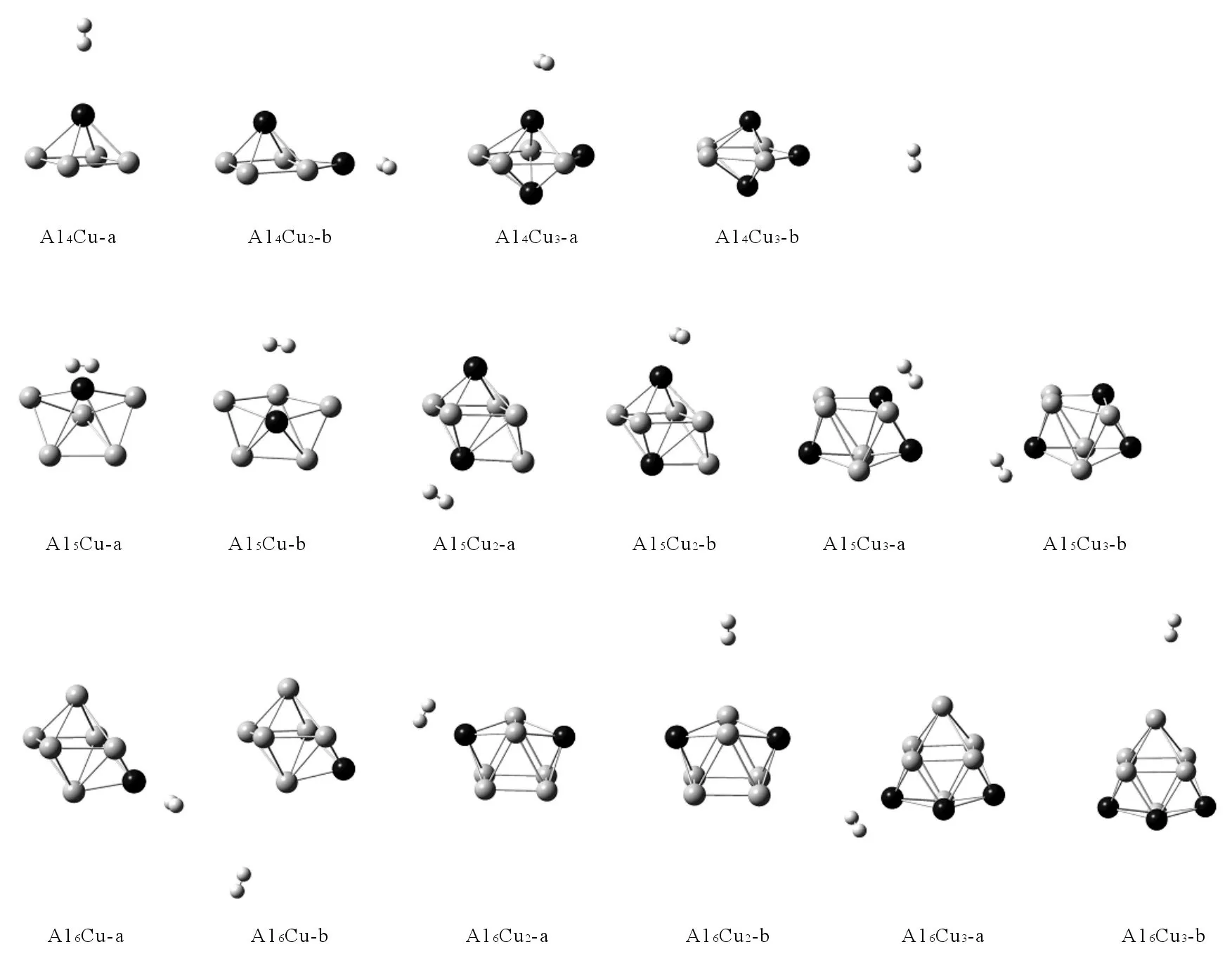
图4 氢分子在AlnCum(n=4-6，m=1-3)团簇上的吸附结构图

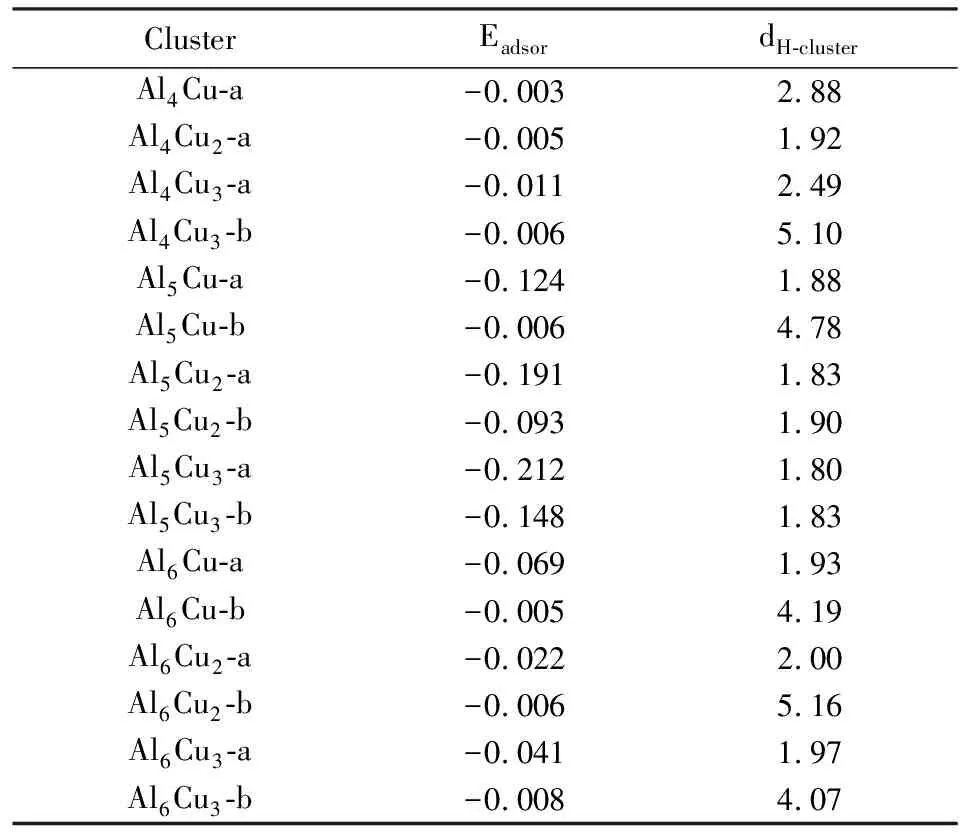
表2 氢分子在AlnCum(n=4-6；m=1-3)团簇

3 结论

本文采用遗传算法结合密度泛函理论对AlnCum(n=4-6，m=1-3)团簇的几何结构进行了详细的搜索分析，计算了团簇的结合能、平均结合能，优化了氢分子在团簇上的吸附结构，计算了氢分子的结合能。首次报道了2个和3个Cu原子掺杂的AlnCum(n=4-6，m=2-3)团簇的稳定结构。Cu原子掺杂Al团簇后，分散的处在团簇的表面，除Al4Cu3、Al5Cu2和Al6Cu，掺杂Cu原子使纯Al团簇的稳定性增强。氢分子倾向于吸附在原子的顶位，在Al原子顶位的吸附非常弱；在Cu原子顶位的吸附较强，最大吸附能可达到-0.212 eV，达到了氢分子物理吸附的理想吸附强度。