基于降阶模型的翼型颤振主动抑制研究

高国柱，周 萌

(中国电子科技集团公司第三十八研究所 浮空平台部，合肥 230088)

0 引言

随着飞行器设计技术的发展以及对飞行包线运用的日益扩大，颤振问题在飞行器设计中越来越受到重视并成为研究热点。目前在工程中以线性无黏化假设的偶极子网格法分析非定常气动力，再耦合计算结构动力学(Computational Structural Dynamics，CSD)建立气动弹性分析系统求解颤振，但在跨声速时该方法的预测精度大幅下降。而基于计算流体动力学(Computational Fluid Dynamics，CFD)耦合计算结构动力学的高精度气动弹性分析方法迅速发展，成为研究人员分析与改善跨声速颤振问题时的首选。但是，基于CFD/CSD的高精度气动弹性时域分析方法计算效率低下，严重制约着其在工程中的应用，而基于系统辨识的降阶模型(Reduce-order Model, ROM)是解决这一问题的主要方法之一。

系统辨识降阶模型的原理是输入外部位移信号q(t)激励系统，通过CFD求解器得到系统的时域响应f(t)，在此过程中，不关心CFD求解器的求解过程，全程将其看作是一个黑箱子，然后根据输入信号和系统由输入信号得到的气动力响应构建相应的映射关系，从而建立ROM，基于自回归滑动平均模型(Auto-Regressive Moving Average Model，ARMA)的非定常气动力降阶模型是一种基于时间序列的降阶模型[1]，在保持气动力计算精度的同时计算效率提高了1～2个数量级。Cowan等人[2]首先将ARMA的非定常气动力降阶模型应用到气动弹性领域，采用3211信号作为激励信号输入系统，并预测了跨声速标准算例AGARD445.6机翼的颤振边界。Gupta[3]和张伟伟[4]等人也采用该模型开展了跨声速气动弹性研究。祝志文等人[5]根据CFD数值模拟的输入和输出，建立起桥梁断面绕流系统的离散时间气动ARMA ROM，进而识别桥梁断面颤振导数。Attar等人[6]通过研究，构建了能够描述一定非线性的ARMA ROM。

国内外的研究人员在气动弹性系统辨识方面取得了丰硕的成果，但在基于ROM的颤振抑制方面研究较少。本文耦合开环气动弹性分析系统和操纵面模态对应的气动状态空间方程，发展了一套伺服气动弹性分析系统，为提高颤振边界进行主动控制律设计，通过算例验证了有效性。

1 气动弹性系统降阶模型

将结构运动方程和基于ARMA模型的气动力降阶模型方程联立，得到气动弹性系统的状态空间形式的控制方程，文献[7]：

其中，x表示位移，Aa、Ba、Ca和Da是气动力降阶模型中辨识出的参数，As、Bs和Cs是输入的结构参数，q表示自由来流动压，下标s对应的是结构参数，下标a对应的是气动力参数。

在文献[8-10]中，通过二维两自由度跨声速气动弹性标准算例验证了该计算方法的精度，证明了该ROM可用于后续的气弹分析。

2 气动弹性颤振主动抑制模型

由式(1)建立的基于ARMA模型的气动弹性分析，可以将开环气动弹性模型改写为：

由文献[8]中ARMA降阶模型可以建立操纵面模态所对应的气动状态空间方程：

其中，下标ac表示操纵面模态建立的气动力降阶模型，fac表示输出的广义气动力；Aac、Bac、Cac、Dac表示操纵面模态气动力降阶模型中辨识出的参数。

对于控制系统而言，建立一个相应的状态空间方程：

对式(4)作简化，即

令xase=[xas,xac]，将式(2)(3)(5)串联起来可以得到伺服气动弹性系统的状态方程：

本文运用线性二次调节器(Linear Quadratic Ragulator, LQR)最优化控制律设计方法设计了主动颤振抑制系统。

3 颤振主动抑制控制律设计

研究对象为二维气动伺服弹性NACA0012翼型，一个相对弦长为25%的操纵面安装在翼型的后缘作为控制机构。采用上述方法设计控制律作为操纵面运动规律实现颤振抑制，提高颤振边界。在计算过程中，忽略控制面对结构的影响，将结构看成一个经典的二维两自由度颤振问题。典型的二维翼型带控制面的几何和结构参数定义如图1所示，xa表示弹性轴到中心的距离，a表示重心到中心的距离，Ka为翼型关于刚心的俯仰刚度，Kh为翼型关于刚心的沉浮刚度，b为参考长度(弦长的1/2)，h表示沉浮位移，该构型的结构参数[11]为：M/m=1.0，xa=0.2，ra=0.539，弹性轴位置a=-0.2，频率比ωh/ωa=0.343，质量比μ=100。

翼型后缘控制面偏转角以β(t)表示。引入反馈控制后，β(t)可以通过下式得到：

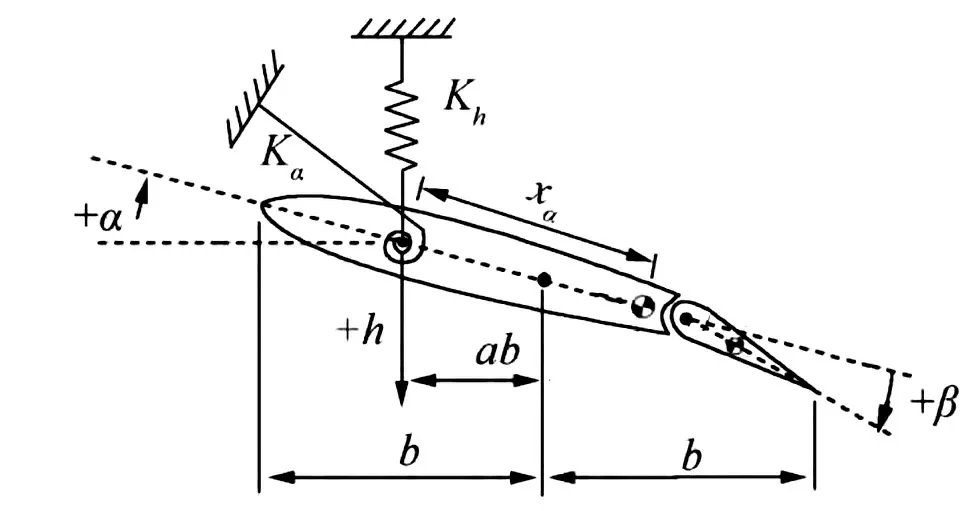
图1典型的二维翼型带控制面的几何和结构参数定义

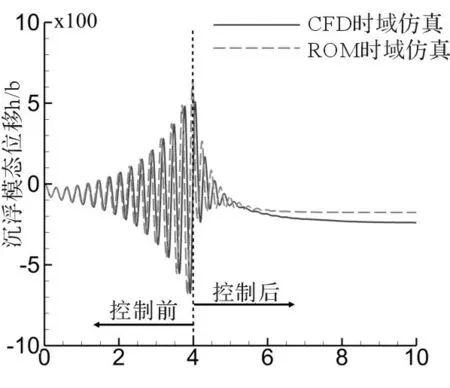
自由来流马赫数Ma=0.80时气动弹性系统仿真结果如图2所示，此开环系统的颤振临界速度为无量纲颤振速度V/(ωab)=3.54 ，选取颤振点设计控制律。通过LQR设计的控制律为k1=0.327、k2=0.134、k3=-2.160、k4=0.169，此时采用频域计算方法得到闭环系统的颤振临界速度为V/(ωab)=4.50 。与开环的结果对比，LQR最优控制方法将颤振临界速度从3.54 提高到了4.50 ，即引入反馈控制后，大幅度提高了颤振临界速度。在Ma=0.80，V/(ωab)=4.0 状态下(此速度下开环系统是不稳定的)，将设计的控制律加入到基于ROM模型的气动弹性时域仿真中，在气动弹性系统的前4 s，采用开环系统分析，控制面不偏转；当t>4 s时，加入控制系统，气动弹性系统由开环转为闭环，此时控制面开始偏转。图2(a)和图2(b)给出了在控制前后CFD和ROM计算的控制面的结构位移响应历程，从图中可以看出，在未施加控制之前，CFD和ROM计算的系统的位移响应是不断发散的，系统是不稳定的；在施加控制之后，CFD和ROM计算的系统响应不断收敛，因此闭环系统是稳定的。由此说明了设计的控制律能有效的抑制颤振导致的系统不稳定，提高了颤振边界，通过CFD和ROM的时域仿真对比可以看出，其位移响应历程基本是一致的，验证了ROM的精度。

选取每个马赫数和相应的临界颤振速度为控制律设计工况，NACA0012翼型开环和闭环颤振边界对比如图3所示。结果表明，设计的控制率有效地抑制了颤振不稳定，闭环的颤振临界速度比开环的颤振临界速度普遍提高了20%左右。这是由于闭环系统以前一时刻或前一段时间的沉浮位移响应和俯仰位移响应为输入，反馈得到当前时刻操纵面运动规律而控制操纵面。从能量的角度分析[12]，颤振的能量来源于气动力做功，经典颤振问题中不同结构模态相互耦合从气流中汲取能量，而后缘操纵面偏转抑制沉浮模态和俯仰模态相互耦合从气流中汲取能量，从而提高颤振边界。

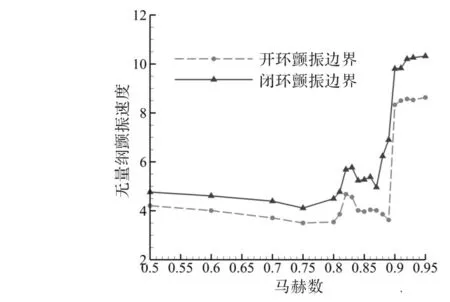
图3NACA0012翼型开环和闭环颤振边界对比

4 结语

通过ROM与CFD/CSD的无量纲颤振速度计算结果，表明基于ROM计算的无量纲颤振速度准确性及精度高，该ROM可用于气弹分析，为有效抑制翼型颤振提供一种快速评估和设计方法；通过建立的闭环气动弹性分析系统进行控制律设计，并分别采用ROM技术和CFD技术进行数值模拟，结果表明：使用开、闭环气弹系统时基于ROM和CFD分别仿真时域仿真结果吻合较好；基于ROM技术设计的控制律能够有效地抑制颤振，闭环的颤振临界速度比开环的颤振临界速度普遍提高了20%左右。