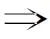
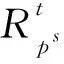ZpZps[ξ]-线性斜常循环码

宋贤梅, 刘 玮, 陈法龙

(安徽师范大学 数学与统计学院, 安徽 芜湖 241002)

1 预备知识

设-:Zps→Zp;a0+a1p+…+as-1ps-1a0是模p的同态, 其中ai∈ZP(i=0,1,…,s-1), 其可以自然扩展至Zps[x]到Zp[x]的同态.设h(x)是Zps上的首一多项式, 若是Zp上的不可约多项式, 则称h(x)为Zps上的基本不可约多项式.若是Zp上准素多项式, 则称h(x)是Zps上的基本准素多项式.

命题1[13]设h(x)是Zps上次数为m的首一基本准素多项式, 则Zps[x]/〈h(x)〉是一个Galois环, 其特征是ps, 基数是psm.

设h(x)是首一不可约多项式,ξ=x+〈h(x)〉∈Zps[x]/〈h(x)〉, 则ξ是h(x)的根,Zps[x]/〈h(x)〉中的每个元素可以写成

a0+a1ξ+a2ξ2+…+am-1ξm-1,ai∈Zps, 0≤i≤m-1,

因此Zps[x]/〈h(x)〉=Zps[ξ], 其中Zps[ξ]={a0+a1ξ+a2ξ2+…+am-1ξm-1|ai∈Zps, 0≤i≤m-1}.

考虑同态:

r=a0+a1ξ+a2ξ2+…+am-1ξm-1

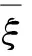
其中加法是通常的向量加法, 数乘定义为

其中γ∈Zps[ξ], (α,β)∈ZpZps[ξ], 则ZpZps[ξ]是一个Zps[ξ]-模.

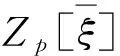
u=(a0,a1,…,ar-1,b0,b1,…,bt-1),

u与v的内积为

根据内积定义,ZpZps[ξ]上线性码C的对偶码C⊥定义为

易知, 如果C是ZpZps[ξ]上的线性码, 则C⊥也是ZpZps[ξ]上的线性码.

2 ZpZps[ξ]上的线性码

定理1设C是ZpZps[ξ]上的一个线性码, 则C置换等价于一个ZpZps[ξ]-线性码, 其生成矩阵标准形为

(1)

证明: 设Ct表示C中元素最后t个坐标集, 因此Ct是Zps[ξ]的线性码, 且有生成矩阵

(2)

加前r列坐标到矩阵(2)上, 有

最后进行必要的行列变换即可得到生成矩阵(1).

注1ZpZps[ξ]线性码的型是(r,t,k0,k1,…,ks).

例1设C是一个Z3Z9[ξ]线性码, 且r=2,t=3,ξ是不可约多项式x2+x+1∈Z9[x]的根, 其生成矩阵为

经过必要的行列变换可得如下标准形:

1)C是形如(2,3,2,2,0)；

2)C有|C|=32.292.3=43 046 721码字.

3 ZpZps[ξ]上的斜常循环码

θp:Rp→Rp,

θps:Rps→Rps,

a0+a1ξ+…+am-1ξm-1→a0+a1ξp+…+am-1ξp(m-1).

θ(k0,k1,…,kr-1,l0,l1,…,lt-1)=(θp(k0),θp(k1),…,θp(kr-1),θps(l0),θps(l1),…,θps(lt-1)).

定义1斜多项式环Ri[x;θi](i=p或ps)是一个多项式集合:

Ri[x;θi]={a0+a1x+…+anxn|aj∈Ri,j=0,1,…,n},

其中: 加法是通常的多项式加法; *乘定义为

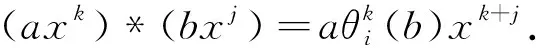
则Ri[x;θi]是一个非交换环,

Z(Rps[x;θps])={f(x)∈Rps[x;θps]|f(x)g(x)=g(x)f(x), ∀g(x)∈Rps[x;θps]}

称为Rps[x;θps]的中心子环, 是一个交换环.Z(Rps[x;θps])中的多项式称为中心多项式.

类似于文献[8]的证明方法, 对于斜多项式环Rps[x;θps]也有类似的带余除法.设f(x),g(x)∈Rps[x;θps],g(x)的首项系数是单位, 则存在q(x),r(x)∈Rps[x;θps], 使得f(x)=q(x)*g(x)+r(x), 其中r(x)=0或deg(r(x))

命题2设f(x)=xt-α∈Rps[x;θps],α∈Rps是单位,θps的阶为m, 则f(x)∈Z(Rps[x;θps])当且仅当m|t且θps(α)=α.特别地,xt-1∈Z(Rps[x;θps])当且仅当m|t.

证明: 假设f(x)∈Z(Rps[x;θps]), 则

x*(xt-α)=xt+1-θps(α)x, (xt-α)*x=xt+1-αx.

比较系数得θps(α)=α.对任意的a∈Rps, 有

反之, 对任意的ax∈Rps, 有

由条件m|t且θps(α)=α有ax*(xt-α)=(xt-α)*ax.从而对任意的g(x)∈Rps[x;θps], 有

g(x)*(xt-α)=(xt-α)*g(x).

注2由命题2知, 当θps的阶整除t且θps(α)=α时, 〈xt-α〉是一个理想.因此, 下面讨论均要求θps的阶整除t且θps(α)=α.

下面考虑Rps上斜常循环码的生成多项式及其相关性质, 先给出Rps上斜常循环码的定义,θps是Rps上的自同构.

由定义2知, 码Ct是θps-α-循环码当且仅当Ct是Rps[x;θps]/〈xt-α〉上的左Rps[x;θps]-子模.

类似文献[10]中定理4的证明方法可得如下结论：

引理1假设Ct是Rps上长为t的斜常循环码, 且包含一个次数最低的多项式gt(x), 其首项系数是单位, 则Ct是由gt(x)生成的线性码, 其中gt(x)|r(xt-α).进一步,Ct有基底

{gt(x),x*gt(x),…,xt-deg(gt(x))-1*gt(x)}.

证明: 设Ct是θps-α-循环码, 则对任意(a0,a1,…,at-1)∈Ct, 有

(αθps(at-1),θps(a0),…,θps(at-2))∈Ct,

而α是单位, 进而有

于是

θps(α-1)a0θps(bt-1)+a1θps(b0)+a2θps(b1)+…+at-1θps(bt-2)=0.

注意到θps(α-1)=α-1, 因此

〈(α-1θps(bt-1),θps(b0),…,θps(bt-2)),(a0,a1,…,at-1)〉=0,

即

定理3设Ct是Rps上长为t的θps-α-循环码, 且A是Ct中次数最低的多项式集合.

1) 若Ct中不存在首一多项式, 则Ct=〈pq(x)〉, 其中q(x)|r(xt-α)(modp);

2) 若A中存在首一多项式, 则Ct=〈g0(x)+pg1(x)〉, 其中:

(g0(x)+pg1(x))|r(xt-α)(modp);g0(x)|r(xt-α)(modp).

3) 若A中不存在首一多项式, 但Ct中存在首一多项式, 则Ct=〈g0(x)+pg1(x),pq(x)〉, 其中q(x)|rg0(x)|r(xt-α)(modp).

证明: 1) 假设Ct中不存在首一多项式, 不妨设g(x)是A中一个首项系数是u的多项式, 则存在首一多项式q(x), 使得g(x)=uq(x),u∈Zps.若u是单位, 则q(x)=u-1g(x)∈C, 与条件矛盾, 因此u是一个零因子, 即u∈〈p〉, 此时得g(x)=npq(x).所以Ct=〈pq(x)〉,q(x)|r(xt-α)(modp).

2) 由引理1知存在g0(x)+pg1(x), 使得Ct=〈g0(x)+pg1(x)〉且g0(x)+pg1(x)|r(xt-α), 因此g0(x)|r(xt-α)(modp).

3) 假设A中存在非首一多项式Q(x), 但Ct中存在首一多项式F(x), 则

Q(x)=pq(x),q(x)∉A, deg(Q(x))=deg(q(x)).

不妨令F(x)=g0(x)+pF1(x), 则易知deg(Q(x))

F(x)=g0(x)+p(l1(x)q(x)+g1(x))=g0(x)+pg1(x)+pl1(x)q(x).

所以F(x)=〈g0(x)+pg1(x),pq(x)〉.

假设任意c(x)∈Ct.若c(x)的首项系数是单位, 则存在单位u, 使得c1(x)=u-1c(x)是首一多项式.由上述讨论易知c(x)∈〈g0(x)+pg1(x),pq(x)〉.若c(x)的首项系数不是单位, 由Q(x)的次数最低, 则c(x)∈〈pq(x)〉.综上有c(x)∈〈g0(x)+pg1(x),pq(x)〉, 故Ct=〈g0(x)+pg1(x),pq(x)〉.

最后证明q(x)|rg0(x)(modp).对Q(x)=pq(x)∈A, 存在多项式p(x),r(x)∈Zps[x], 使得

g0(x)+pg1(x)=p(x)pq(x)+r(x),

其中r(x)=0或deg(r(x))

下面考虑ZpZps[ξ]上的斜常循环码生成集.

定义3设C是ZpZps[ξ]上长为r+t的线性码,α∈Rps满足命题2中条件.若对任意的c=(e0,e1,…,er-1,d0,d1,…,dt-1)∈C, 有

θ(c)=(θp(er-1),θp(e0),…,θp(er-2),αθps(dt-1),θps(d0),…,θps(dt-2))∈C,

则称C是ZpZps[ξ]-斜常循环码或θ-α-循环码.

注3C中元素c=(e0,e1,…,er-1,d0,d1,…,dt-1)的多项式形式为

记

Rθ=Rp[x;θp]/(xr-1)×Rps[x;θps]/(xt-α).

设g(x)=g0+g1x+…+gtxt∈Rps[x;θps],(f(x),h(x))∈Rθ, 乘法定义为

g(x)*(f(x),h(x))=(g(x)*f(x)(modp),g(x)*h(x)(modps)),

因此Rθ是左Rps[x;θps]-模.易知C是ZpZps[ξ]-斜常循环码当且仅当C是Rθ的左Rps[x;θps]-子模.

下面给出投影映射.设C是ZpZps[ξ]-斜常循环码, 投影映射

φ:C→Rps[x;θps]/(xt-α),

(f1(x),f2(x))→f2(x).

易知φ是一个左Rps[x;θps]-模同态, Kerφ是C的子模,φ(C)是左Rps[x;θps]-子模.

进一步, 结合定理3的结论可得ZpZps[ξ]-斜常循环码的生成多项式.

定理4设C是ZpZps[ξ]-斜常循环码.

1) 若φ(C)=〈pq(x)〉, 则C=〈(f(x),0),(l1(x),pq(x))〉, 其中q(x)|r(xt-α)(modp), 且存在l1(x)满足f(x)|rhq(x)l1(x)(modp), 其中xt-α=hq(x)q(x)(modp).

2) 若φ(C)=〈g0(x)+pg1(x)〉, 则C= 〈(f(x),0),(l(x),g0(x)+pg1(x))〉, 其中f(x)|r(xr-1)(modp),g0(x)+pg1(x)|r(xt-α)且deg(l(x))

3) 若φ(C)=〈(g0(x)+pg1(x),pq(x))〉, 则

C=〈(f(x),0),(l(x),g0(x)+pg1(x)),(l1(x),pq(x))〉,

其中f(x)|r(xr-1)(modp),q(x)|rg0(x)|r(xt-α)(modp).

证明: 仅证明2), 类似可证明1),3).

假设φ(C)=〈g0(x)+pg1(x)〉, 则易知

Ker(φ)={(f(x),0)∈C|f(x)∈Rp[x;θp]/(xr-1)}.

设I={f(x)∈Rp[x;θp]|(f(x),0)∈Ker(φ)}是由主理想生成的Rp[x;θp]-子模, 从而可假设I=〈f(x)〉.对任意的(w(x),0)∈Ker(φ), 则w(x)∈I且w(x)=w1(x)f(x),w1(x)∈Rp[x;θp], 因此(w(x),0)∈〈(f(x),0)〉, 从而Ker(φ)=〈f(x),0〉且f(x)|rxr-1(modp).根据第一同构定理,C/Ker(φ)≅φ(C).易知

C=〈(f(x),0),(l(x),g0(x)+pg1(x))〉.

最后证明f(x)|rhg0(x)l(x)(modp), 由于xt-α=hg0(x)(g0(x)+pg1(x)), 于是

hg0(x)*(l(x),g0(x)+pg1(x))=(l(x)hg0(x),0,),

因此l(x)hg0(x)∈〈f(x)〉.

定理5设C=〈(f(x),0),(l(x),g0(x)+pg1(x)),(l1(x),pq(x)〉是ZpZps[ξ]中的一个斜常循环码, 则S=S1∪S2∪S3是C的极小生成集, 其中:

证明: 设c(x)∈Rθ是C的一个码字, 则

c(x)=e1(x)*(f(x),0)+e2(x)*(l(x),g0(x)+pg1(x))+e3(x)*(l1(x),pq(x)),

其中e1(x),e2(x),e3(x)∈Rps[x;θps].若deg(e1(x))

e1(x)=q1(x)hf(x)+r1(x),

其中r1(x)=0或deg(r1(x))

e1(x)*(f(x),0)=(q1(x)hf(x)+r1(x))*(f(x),0)=r1(x)*(f(x),0),

于是e1(x)*(f(x),0)∈S1.

若deg(e3(x))

e3(x)=q3(x)hq(x)+r3(x),

其中r3(x)=0或deg(r3(x))

由于f(x)|rhq(x)l1(x), 因此q3(x)*(hq(x)l1(x),0)∈S1, 而r3(x)*(l1(x),pq(x))∈S3, 故有

e3(x)*(l1(x),pq(x))∈S1∪S3.

若deg(e2(x))

e2(x)=q2(x)hg0(x)+r2(x),

其中r2(x)=0或者deg(r2(x))

这里

r2(x)*(l(x),g0(x)+pg1(x))∈S2.

(3)

下面讨论q2(x)hg0(x)*(l(x),g0(x)+pg1(x)).由于f(x)|rhq(x)l1(x)(modp),f(x)|rhg0(x)l(x)(modp), 因此存在u(x), 使得

u(x)f(x)=hq(x)l1(x)+hg0(x)l(x)(modp).

故hg0(x)l(x)=u(x)f(x)-hq(x)l1(x)(modp), 从而

又由于hq(x)q(x)=hg0(x)g0(x)(modp), 因此

注意到q2(x)u(x)*(f(x),0)∈S1, 于是

q2(x)hg0(x)*(l(x),g0(x)+pg1(x))∈S1∪S3.

(4)

由式(3),(4)可知

例2设C是R3[x,θ3]/(x8-1)×R9[x,θ9]/(x8-1)上的Z3Z9[ξ]-循环码,ξ是Z3[x]和Z9[x]上不可约多项式x2+x+1的根.考虑C是由〈(f(x),0),(l(x),g0(x)+3g1(x))〉生成的, 其中:f(x)=2+x+2x2+x3;g0(x)=7+6x+x4;g1=1+x;l(x)=1+x2; 且

通过计算可得如下多项式：

根据定理5, 得到Z3Z9[ξ]-斜循环码C的生成矩阵为