2020年高考数列命题预测
许少华


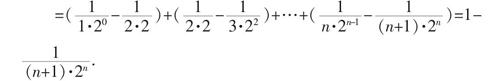
数列在近年全国高考命题中的要求不太高,理科2016、2017、2018连续三年都是命题客观性试题,2019年高考除了命客观性试题之外,在概率统计的运算中涉及了数列的技能与技巧. 文科从2015年至今一直都是既有客观性试题也有主观性试题.可以看出:虽然这一内容的难度要求在降低,但它在高考试卷的中存在性是不容忽视的. 现在到了2020年高考复习的关键时刻了,面对数列,我们如何编织一张不大不小的“网”,既能网住所有,又不至于太大,而浪费呢?下面谈谈我们对2020年高考数列命题的预测,供参考.
一、考查基础知识与基本运算
基础知识与基本运算永远是数列中的一个小“热点”,细心的你一定注意到了,不管是全国卷中的哪一套卷都有这类试题,此类题不难,但要细心.
例1. 已知各项均为正数的等比数列{an}的前4项为和为15,且a5=3a3+4a1,则a3=( )
A. 16 B. 8 C. 4 D. 2
解析一利用方程思想列出关于a1,q的方程组,求出a1,q,再利用通项公式即可求得a3的值. 设等比数列{an}的公比为q,易知q>0,
由已知得a1+a1q+a1q2+a1q3=15,a1q4=3a1q2+4a1,解得a1=1,q=2,∴ a3=a1q2=4,故选C.
解析二易知q>0,若公比q=1,则a5=3a3+4a1不成立,从而■=15,a1q4=3a1q2+4a1,同样解得a1=1,q=2,∴ a3 = a1q2=4. 此法明显不如解法1好.
例2. 记Sn为等差数列{an}的前n项和.若a4+a5=24,S6=48,则{an}的公差()
A. 1 B. 2 C. 4 D. 8
解析因为a4+a5=a1+3d+a1+4d=24,S6=6a1+■d=48,联立求得2a1+7d=24……①6a1+15d=48……② ①×3-②得(21-15)d=24,∴ 6d=24,∴ d=4,选C.
点评上述两例就是基本运算型试题,此题年年有,考法也相似. 没有难度,只要熟悉基本公式,再细心运算都产生正确答案.
二、在客观性试题中设计创新问题
我们知道:高考每年都会出现一部分创新试题. 为了使创新不至于对考生分数产生太大影响,这些试题一般都出现在客观性试题中,首先是因为它的分值不高,其次,在产生答案的过程中还存在一些侥幸与运气(如,2019年高考第5题),这些题的落点放在数列上也是完全可以的.
例3. 几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,在接下来的三项式26,21,22,依次类推,求满足如下条件的最小整数N:N>100且该数列的前项和为的整数幂.那么该款软件的激活码是()
A. 440 B. 330 C. 220 D. 110
解析一设首项为第1组,接下来两项为第2组,再接下来三项为第3组,以此类推.第n组的项数为n,则前n组的项数和为■由题,N>100,令■>100→n≥14且n∈N*,即N出现在第13组之后. 由于,第n组的和为■=2n-1;n组总共的和为■-n=2n+1-2-n;若要使前N项和为2的整数幂,则N-■项的和2k-1应与-2-n互为相反数,即2k-1=2+n(k∈N*,n≥14);k=log(n+3)→n=29,k=5则N=■+5=440.
解析二先分组,第一组:20;第二组:20,21;第三组:20,21,22;…;第k组:20,21,…,2k-1. 设该数列的第N项在第k组中的第m项(1≤m≤k,m∈N).
由题意可得:N=1+2+…+(k-1)+m>100.
即■+m>100?圯■+k>100?圯k≥14.
该数列的前N和为:
20+(20+21)+(20+21+22)+…+(20+21+…+2k-2)+(20+21+…+2m-1)
=(21-1)+(22-1)+…+(2k-1-1)+(2m-1)
=(21+22+…+2k-1)-(k-1)+(2m-1)=2k+2m-k-2.
因为1≤m≤k,则2≤2m≤2k,于是2k+2-k-2≤2k+2m-k-2≤2k+2k-k-2.
即2k-1<2k+2m-k-2<2k+1.
由于该数列的前N和为2方幂,那么2k+2m-k-2=2k,由此得2m=k+2.
由k≥14可知,当k=14時,m=4,此时,N=1+2+…+13+4=95<100.
当k=30时,m=5,此时,N=1+2+…+29+5=440,选A.
例4. 设数列{an}满足an+1= ■ -nan+1且a1≥3,若数列bn=■的前n项和为Tn,则Tn满足()
A.Tn≥■B.Tn≤■C.Tn≥■D.Tn≤■
解析首先,由a1≥3可得an≥n+2.
因为ak≥k+2,那么ak+1=ak(ak-k)+1≥(k+2)(k+2-k)+1≥k+3.
于是an≥n+2.
其次,由an≥n+2及an+1= ■ -nan+1.
得an+1=an(an-n)+1≥an(n+2-n)+1=2an+1得:■≤■,
∴■=■·(■)·(■)·…·(■)≤■·(■)n-1.
又由于a1≥3,
因而Tn=■+■+…+■≤■[1+■+…+(■)n-1]=■≤■.
点评上述两题的创新特点都十分明确,一道以实际应用为背景,借助数列考查解决问题的能力,一道直接考查应用的技能与技巧. 两道题都有难度也有灵活性,数学味十足.
三、利用主观性试题,考查两类特殊数列的定义与基本公式
数列的主观性试题不是每年都有,当有的时候,有时是建立在等差与等比概念的基础上,考查这两类特殊数列的定义及基本公式的应用,此类题难度不大,是广大考生普遍得分之题.
例5. 已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(1)证明: {an+bn}是等比数列, {an-bn}是等差数列;
(2)求{an}和{bn}的通项公式.
解析(1)由题设得4(an+1+bn+1)=2(an+bn),即an+1+bn+1= ■(an+bn).
又因为a1+b1=l,所以{an+bn}是首项为1,公比为■的等比数列.
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以{an-bn}是首项为1,公差为2的等差数列.
(2)由(1)知,an+bn=■,an-bn=2n-1.
所以an=■[(an+bn)+(an-bn)]=■+n-■,
bn=■[(an+bn)-(an-bn)]=■-n+■.
例6. 已知数列{an}的前n项和为Sn,a1=1,an≠0,anan+1=?姿Sn-1,其中?姿为常数.
(Ⅰ)证明:an+2-an=?姿;(Ⅱ)是否存在?姿,使得{an}为等差数列?并说明理由.
解析(Ⅰ)由题设anan+1=?姿Sn-1,an+1an+2=?姿Sn+1-1,两式相减,an+1(an+2-an)=?姿an+1,由于an≠0,所以an+2-an=?姿.
(Ⅱ)由题设a1=1,a1a2=?姿S1-1,可得a2=?姿1-1,由(Ⅰ)知a3=?姿+1.
假设{an}为等差数列,则a1,a2,a3成等差数列,∴a1+a3=2a2,解得?姿=4;
证明?姿=4时, {an} 为等差数列:由an+2-an=4知:
数列奇数项构成的数列{a2m-1}是首项为1,公差为4的等差数列a2m-1=4m-3.
令n=2m-1,则m=■,∴ an=2n-1(n=2m-1).
数列偶数项构成的数列{a2m}是首项為3,公差为4的等差数列a2m=4m-1.
令n=2m,则m=■,∴ an=2n-1(n=2m).
∴ an=2n-1(n∈N*),an+1-an=2.
因此,存在?姿=4,使得{an}为等差数列.
点评这两题都是直接、间接的证明等差数列与等比数列,求解时只需将递推式子稍作变形即可产生结论.
四、建立在特殊数列的基础上,考查求和的常规技能
数列求和是数列中一类重要题型,常见的基本方法有:分组求和、裂项求和与错位相减,这些也构成了数列中的一类常规考题,第一问与特殊数列结合,第二问可以考查求和的常规技能.
例7. 已知公比不为1的等比数列{an}的前n项和为Sn,满足S6=■且a2,a4,a3成等差数列.
(1)求等比数列{an}的通项公式.
(2)设数列{bn}满足bn=nan,求数列{bn}的前n项和为Tn.
解析(1)设数列{an}的首项为a1,公比为q由题意得:
S6=■,a2+a3=2a4?圯■=■,a1q+a1q2=2a1q3?圯a1=3,q=-■.
从而an=a1qn-1=3(-■)n-1.
(2)由(1)得bn=3n(-■)n-1.
由
Tn=3×(-■)0+3×2(-■)+3×3(-■)2+…+3n×(-■)n-1…(1)-■Tn=3×(-■)+3×2(-■)2+3×3(-■)3+…+3n×(-■)n…(2)(1)-(2)得■Tn=3×(-■)0+3×(-■)+3(-■)2+…+3(-■)n-1 -3n×(-■)n,
整理得:Tn=■-(2n+■)(-■)n.
点评当我们面对等比数列(或等差数列)与通项公式及前n项和公式有关的问题时,一般都是先设出首项与公比(差),通过列、解方程组产生结论. 同时对于错位相减的方法应用也是最为常见的命题热点,应引起我们的关注.
例8. 等差数列{an}与等比数列{bn}满足:a1=b1+1,a2=b2=4且公差比公比小1.
(1)求{an}与{bn}的通项公式
(2)设数列{cn}满足cn=■,试求数列{cn}的前n项和Tn.
解析(1)设等差数列的公差为d,等比数列的公比为q,则a1=b1+1,a1+d=2,b1q=4,q=d+1?圯a1=3,b1=2,q=2,d=1.
于是{an}与{bn}的通项公式分别为an=n+2,bn=2n.
(2)由cn=■得cn=■=■(■-■)=■-■.
于是Tn=c1+c2+…+cn
=(■-■)+(■-■)+…+(■-■)=1-■.
点评本题第二问的求解很有特点,若发现了裂项、又能顺利应用,也许会很快产生结论,否则,可能会陷入复杂与繁冗的运算与推理之中.
五、建立在简单递推式的基础上,考查基本运算与转化
递推式是表示数列的常用方法之一,由于递推式的形式可以比较简单也可以比较复杂、甚至是比较难. 因此由递推式确定的数列的问题往往有难度,但近年是以中档及偏下为主.
例9. 数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+■}是等比数列,并求{an}的通项公式;
(2)证明:■+■+…+■<■.
解析(1)∵an+1=3an+1,∴an+1+■=3(an+■),即:■=3.
又∵a1+■=■,∴{an+■}是以■为首项, 3为公比的等比数列.
∴ an+■=■·3n-1,即an=■.
(2)证明:由(1)知an=■,∴■=■≤■=■(n∈N*),
∴■+■+…+■≤1+■+■+…+■=■=■[1-(■)n] <■.
故:■+■+…+■<■.
例10. 正项数列{an}满足a1=2,且2nan+1+2n2=an+1an+nan.
(1)求数列{an}的前n项和Sn.
(2)求证:对一切正整数n,有■+■+…+■<■.
解析(1)由2nan+1+2n2=an+1an+nan?圯(an-2n)(an+1+n)=0,由于an>0,
得an=2n,从而Sn=2×1+2×2+…+2n=n(n+1).
(2)法一:由■=■=■·■<■·■-■.
■+■+…+■
<■(■-■)+(■-■)+…+■-■
=■(■-■)=■-■<■.
法二:由■=■<■=■(■-■),
那么■+■+…+■
<■+■[(■-■)+(■-■)+…+(■-■)]=■-■<■.
法三:由■=■=■<■=■-■.
那么
■+■+…+■<(■-■)+(■-■)+…+(■-■)=■-■<■.
点评本题第二问,无论是哪种方法,也都是建立在通项的基础上,对通项进行放缩,然后,再进行裂项,最后完成求解的.可以看出裂项依然是关键.
六、与其它知识结合考查数列基本技能交汇性应用
试题的交汇性,是近年高考试题的一大特色,数列中我们依然要关注其交汇性,数列会与哪些知识交汇呢?
1. 集合与数列交汇
例11. 已知数集序列{1},{3,5},{7,9,11},{13,15,17,19},…,其中每一个数集都由连续正奇数构成,每一个数集都比前一个数集多一个数,并且每一数集的最大数与后一个数集的最小值是连续奇数,则第n个数集的各数之和为___________.
解析根據规律可以得到第n个数集共有n个奇数,且最小的奇数是第n-1个数集中最大的数加2.
由于前n-1个数集共有1+2+…+(n-1)=■个数,于是第n-1个数集中最大的数为2×■-1=n2-n-1,于是第n个数集中最小的奇数是n2-n+1.
那么Sn=n(n2-n+1)+■×2=n3.
点评本题通过对集合中元素个数的规律进行研究,发现了第个数集中元素的数量. 再通过对元素特点的分析,进一步产生第个数集中元素的构成,然后产生结论.
2. 与函数交汇
例12. 已知f(x)=x+1,g(x)=2x+1数列{an}满足:a1=1,an+1=f(an)(n为奇数)g(an)(n为偶数)则数列{an}的前10项的和为___________.
解析:由a1=1,结合递推式可得a2=2.
由于a2n+2=a2n+1+1=(2a2n+1)+1=2a2n+2?圯a2n+2+2=2(a2n+2),显然,数列{a2n+2}是以a2+2=4为首项,以2为公比的等数列,所以a2n+2=(a2+2)·2n-1?圯a2n=2n+1-2.
又由a2n+1=2a2n+1=2(a2n-1+1)+1=2a2n-1+3?圯a2n+1+3=2(a2n-1+3),显然,数列{a2n-1+3}是以a1+3=4为首项,以2为公比的等数列,所以a2n-1+3=(a1+3)·2n-1?圯a2n-1=2n+1-3.
那么,S10=(a1+a3+…+a49)+(a2+a4+…+a50)
=(22-3+23-3+…+226-3)+(22-2+23-2+…+226-2)=228-133.
点评本题借助于分段递推式将数列的通项公式求和,通过通项公式将待求和的结果进行分组,最后产生结论. 求解难点在于通过递推式产生等比数列的结论.
3. 与线性规划交汇
例13. 设不等式组x>0,y>0,y≤-nx+4n(n≥1,n∈Z)所表示的平面区域为Dn的整点个数为an,则■(a1+a3+a5+…+a2007)=_________.
解析首先作直线y=-nx+4n,再结合x>0,y>0,可得可行域为右图所示的三角形区域,显然,当x=1时,y=3n,此时整点的个数为3n;当x=2时,y=2n,此时整点的个数为2n;当x=3时,y=n,此时整点的个数为n.
故可行域内整点的个数为an=3n+2n+n=6n.
那么■(a1+a3+a5+…+a2007) =■(6×1+6×3+…+6×2007)=■×6×■×1004=3012.
点评本题首先作出可行域,然后再求整点的数量;稍留心会发现,整点其实就在三条直线x=1、x=2及x=3上,而在这三条线上的整点个数正好是3n、2n及n个,得到这三个数据之后,再求和就简单了.
数列的预测,我们就说这些,虽然,命题降低了难度,但并不表示,数列不重要. 其实,聪明的人会看出更重要了,因为,这里才是真正得分的地方,抓住了分数,高考能不获胜吗?
责任编辑 徐国坚

