利用圆巧解题

俞新龙

因为圆在初中平面几何中有较多的涉及，在高中数学中又有圆锥曲线压身，所以圆的身份比较尴尬：想被重视却重视不起来，从而导致一些能用圆巧妙解决的较难问题无法被有效突破. 本文举例说明.

一、寻找向量中圆的身影，有效突破最值

向量作为高考必考的知识点已经成为高考命题者尝试创新命题的一个重要阵地，近年来在高考和各省市模拟卷中出现了不少有新意的考题，其中有一些考题若能挖掘出题中隐含的“圆”，则问题便能较好的求解.我们知道向量是数形结合体，故一般向量问题都会有两种解决办法：代数法和几何法.下面我们就从这两个方面来进行求解.

例1. 已知■，■，■是平面向量，■是单位向量.若非零向量■与■的夹角为■，向量b满足■-4■·■+3=0，则|■-■|的最小值是（ ）

A. ■-1B. ■+1C. 2D. 2-■

解析：

代数法（坐标法）：如图1建立平面直角坐标系，设■=■=（1，0），■=■，■=■=（x，y），则可知A在射线y=■x（x>0）上，又根据等式■-4■·■+3=0可得（x-2）2+y2=1，所以知B在以（2，0）为圆心、1为半径的圆上. |■-■|的几何意义是线段AB的距离，即圆（x-2）2+y2=1上任意一点与射线y=■x（x>0）上任意一点的距离，故|■-■|的最小值显然是圆心（2，0）到射线y=■x（x>0）的距离■减去圆半径1，故答案为A.

几何法：因为■-4■·■+3=■-4■·■+3■=（■-■）·（■-3■）=0，所以BE⊥BD，如图1所示，则可知B在以ED为直径的圆上，即得B的轨迹为（x-2）2+y2=1，其余做法同代数法，略.

评注：代数法中的圆从方程中能够直观得到，但几何法中的圆需要结合直角三角形直角顶点一定在以斜边为直径的圆上这个性质.

例2. 已知平面向量■，■，■满足|■|=4，■·（■-■）=■·（■-■）=3，当■与■的夹角最大时，■·■=________.

解析：设■=■=（4，0），

代数法（坐标法）：设■=■=（x，y），则根据■·（■-■）=3得x（4-x）+y（-y）=3，化简得（x-2）2+y2=1，即向量■终点A在（2，0）为圆心、1为半径的圆上，同理■终点B也在（2，0）为圆心、1为半径的圆上，如图2所示OA、OB与圆相切时向量■与■的夹角最大，此时A（■，■），B（■，-■），所以■·■=■-■=■.

几何法：由条件等式■·（■-■）=■·（■-■）=3整理得（■-■）2=（■-■）2=1，即知向量■与■是（2，0）为圆心、1为半径的圆上的两个动点，记■=■，■=■，如图2所示OA、OB与圆相切时向量■与■的夹角最大，此时A（■，■），B（■，-■），所以■·■=■-■=■.

评注：配方是个难点，从配方式子中看出轨迹是圆是关键点.

例3. 已知非零向量■，■，■，满足|■|=2，■·■=■|■|，■=■■·■-2，则对任意实数t，|■-t■|的最小值为___________.

解析：设■=■=（2，0），根据条件■·■=■|■|知向量■、■的夹角为30°.

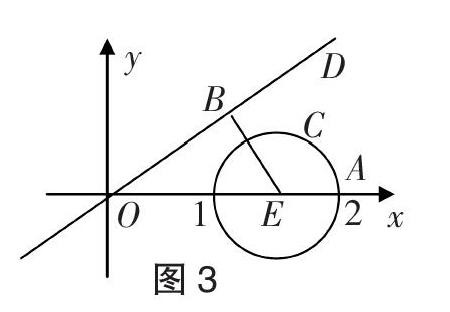
代数法（坐标法）：设■=■=（x， y），则根据■=■■·■-2得x2+y2=3x-2，化简得（x-■）2+y2=■，如图3所示，点B在直线OD：y=■x上运动，点C在以E（■， 0）为圆心、■为半径的圆上运动，因为 | ■-t■ | 的几何意义是圆E上的任意一点到直线OD上的任意一点的距离，故 | ■-t■ | 的最小值为圆心E到直线OD的距离减去圆半径■，即■-■=■.

几何法：由■=■■·■-2得2■=3■·■-4=3■·■-■，从而得（2■-■）（■-■）=0，如图4所示，■=■，2■=■，则2■-■=■，■-■=■，所以■⊥■，又FC1//AC2，所以FC1⊥AC2，因此，向量■的終点C1在以AF为直径的圆上. 下同，略.

评注：本题几何法找向量的终点需要进行平行转化，具有一定的难度.

二、寻找阿波罗尼斯圆的身影，有效突破最值

若 A（a， 0）， B（0， 0），若 | PA |2=k2 | PB |2（k≠1），则（x-a）2+y2= k2（x2+y2），化简得（x+■）2+y2 = （■）2，故P点轨迹是圆心在AB上且半径为 |■| 的圆. 这个轨迹最先是由古希腊数学家阿波罗尼斯发现，简称阿氏圆. 阿氏圆能化身各种形态存在于问题中，需要我们去发现其身影.

例4. 已知■，■是平面内两个互相垂直的单位向量，若向量■满足 | ■-■ |=■，则 | ■+■-■ |+2| ■-■ | 的最小值为________.

解析：如图5，以■=■，■=■，则 |■+■-■  |+2|■-■ |=CD+2CB，设C（x， y），由 | ■- ■ |=■得（x-1）2+y2=■，则根据阿波罗尼斯圆知可在AD上找一点E（1， m）使CD=2CE，即■= 2■，化简得x2-2x+y2-■y+■=0，此方程与点C轨迹方程是一样的，则■=0，■=■，解得E（1，■），则 | ■+■-■ |+2| ■-■ |=2CE+2CB≥2BE，故 | ■+■-■ |+2| ■-■ |≥■.

评注：阿波罗尼斯圆的正用不难，难的是逆用甚至变用，一般求两条比例为1：λ（λ≠1）的线段和就可以试着用阿波罗尼斯圆的性质进行求解.

例5. 已知A，B是平面上的两个定点，平面上的动点C，D满足■=■=k，若对于任意的k≥3，不等式λ≥■恒成立，求实数λ的最小值.

解析：如前所述，阿波罗尼斯圆半径r= |■|=■，即只与两个定点间距离和比值有关. 根据本题条件■=■=k可知，点C、D同在由A、B、k确定的阿波罗尼斯圆上，故CD的最大值就是直径为■，于是■=■，又由于k≥3，所以■=■=■，易知y=■在k≥3上是减函数，故■有最大值■. 根据λ≥■恒成立得λ≥■.

评注：巧妙利用阿氏圆半径，将问题化为函数单调性问题确实事半功倍.

例6. 已知两个不共线的向量■，■，满足 | ■ | =3，| ■+■ | =2|■-■ |，设■，■的夹角为？兹，求cos？兹的最小值.

解析：本题用阿波罗尼斯圆来解答的难点在如何根据条件 | ■+■ | =2|■-■ | 来构造？

记■=■=■，■=■，则■ =■+■，■=■-■，故 | AP | = 2 | CP | ，因此，P在以 | AC | =6、k=2的阿波罗尼斯圆O上. 如图6所示，圆半径r=■=4，因为？兹=∠PBC，所以易知当BP与圆O相切时？兹最大，此时cos？兹取到最小值.

根據等量关系可以求出CO=2，所以BO=5，故相切时可求得BP=3，此时cos？兹=■，所以cos？兹的最小值为■.

评注：从■+ ■、■- ■不难联想到平行四边形，所以可以先用平行四边形对角线性质解题，即|■+ ■ |2+|■- ■ |2=2（|■|2+| ■ |2）=5|■- ■|2，化简得| ■ |2-10cos？兹| ■ | +9=0，由该方程有解得△=100cos？兹2-36≥0，解得| cos？兹 |≥■. 根据|■+ ■|=2|■- ■|可知■，■的夹角？兹为锐角，所以cos？兹≥■.

三、利用直径与圆内外点所成角，有效突破范围

我们知道，圆上的点与直径两端成直角，圆内的点与直径两端成钝角，圆外的点与直径两端成锐角，在解题时一定要有效用起来，以达到突破问题的效果.

例7. 已知圆O：x2+y2=4，A、B为圆上两个动点，满足|AB|=2■，D为线段AB的中点，E（3，m），F（3，m+5）. 当A、B在圆上运动时，存在某个位置使∠EDF为钝角，则实数m的取值范围是_________.

解析：如图7，因为弦长|AB|=2■，所以根据垂径定理知圆心距|OD|=1，所以点D的轨迹方程为x2+y2=1. 当A、B在圆上运动时，存在某个位置使∠EDF为钝角，等价于当D点在圆上运动时，存在位于以AB为直径的圆内的时候. 记AB中点M（3，m+■），则|DM|<■有解，故|DM|min<■. 而|DM|min=|OM|-1=■-1，解得 -■

评注：存在某个位置问题转化为距离的大小关系问题，显然将问题的难度大大降低了.

责任编辑 徐国坚