子群完备码

张 星，王 燕，曲海鹏

(1.烟台大学数学与信息科学学院，山东 烟台264005;2.山西师范大学数学与计算机科学学院，山西 临汾041000)

1 引言与预备知识

令Γ为一有限简单图，设顶点集合为V(Γ)，边集合为E(Γ)．假定C⊆V(Γ)是一个非空子集，t≥1是一个整数．若以C中顶点为圆心，t为半径的圆球形成了顶点集V(Γ)的一个划分，即对任意的v∈V(Γ)，存在唯一的c∈C使得的d(v,c)≤t(d(v,c)表示2个点之间的距离)，则称C为图Γ的完备t-码．由完备码定义可知C是Γ的一个独立集．完备1-码也简称为完备码，在图论中完备1-码也被称为有效控制集或独立的完备控制集．

BIGGS[1]首次提出了图中完备码的概念，而完备码问题起源于编码理论．经典背景下的完备t-码恰好是Hamming图H(n,q)中的完备t-码[1-2]．Hamming图是一类距离传递图，因此距离传递图和结合方案中的完备码问题被广泛研究[1,3-7]．

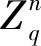
凯莱图中的完备码问题因与编码理论、群论和图论有着密切的联系，近几年来受到了广泛关注．例如，TERADA[8]证明了对共轭封闭的连通集，SL(2,2f)(f>1)任意的凯莱图中都不存在完备码．Gaussian和Eisenstein-Jacobi图中存在完备t-码的充分条件在文献[9]中给出，后来这些条件又被证明在分圆图中是必要的[10]．ETIENNE[11]利用基础群的不可约特征证明了一类特殊的凯莱图中存在完备码的必要条件．DEJTER和SERRA[12]于2003年提出了在对称群上构造凯莱图的e链寻找完备码的方法．LEE[13]证明了交换群的凯莱图存在完备码当且仅当它是一个完全图的覆盖．在文献[14]中完备码被应用于四维信号空间，产生了一种新的定义在整数四元数商群上的凯莱图，并构建了它的完备1-码[15]．循环图的完备码问题被广泛研究[16-19]．

在某种意义下，有限群的凯莱图的子群完备码类似于线性完备码，而线性完备码可以看作是加法群GF(qn)的子群[17]．若C为Cay(G,X)(其中|X|=k)的一个完备码，由定义易得|G|=|C|(k+1)．显然，|C|是|G|的一个因子.这就引发思考子群作为完备码的条件，文献[16]中给出了子群可作为完备码的一个充要条件．本文将从子群作为凯莱图的完备码当且仅当凯莱图的广义凯莱子集是子群的右(左)陪集代表系这一基本引理出发，从群论的角度探究子群作为完备码要满足的条件．

2 子群完备码

设H是群G的一个子群，取子群H在G中的每个右(左)陪集中的一个元素构成集合S，则称集合S为H在群G的一个右(左)陪集代表系．若H是Cay(G,X)(X={x1,x2,…，xd})的一个完备码，则由完备码的定义可知G=H∪Hx1∪Hx2…∪Hxd，而且H,Hx1,…,Hxd之间两两不交．因此，可以自然地得到下面的引理1．

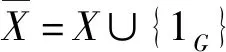
由引理1，H是否是群G的凯莱图的完备码取决于是否存在H的一个右陪集代表系可作为群G的广义Cayley子集．下面的推论1在文献[17]中已给出，这里用群论的方法给出一个新的证明．

推论1 设G是一个有限群，H是群G的一个正规子群．则H是G的凯莱图的完备码当且仅当对每个a∈GH且a2∈H，存在某个h∈H，使得(ha)2=1G成立．因此，奇数阶的正规子群可作为完备码.

证明若H是群G的一个正规子群，则对每个a∈G，由Ha=Ha-1可得(Ha)-1=Ha．

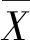
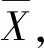
若H是奇数阶的正规子群且存在a∉H,使得右陪集Ha对逆封闭，则Ha中必存一个2阶元．由充分性可得正规子群H是群G的某个凯莱图的完备码，即奇数阶的正规子群可作为完备码．

正如在文献[17]中给出的，即使是群的正规子群也没有一个一般的方法来判断在对逆封闭的右陪集Ha中是否存在2阶元．这就启发我们思考对每个a∈GH，Ha≠Ha-1的正规子群H的情况，即满足条件“a∈H当且仅当a2∈H”的正规子群H可作为完备码的充要条件．为了方便，在下文中规定，若一个子群H满足对任意a∈G，a∈H当且仅当a2∈H，则称子群H满足条件PC．

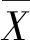
定理1 设G是一个有限群且H是群G的一个子群．H满足条件PC当且仅当Core(G,H)=∩g∈Gg-1Hg包含了群G的所有Sylow 2-子群．

证明必要性：假设子群H满足条件PC．若一个元素的阶是2的方幂，在本文中称这个元素为一个2-元素．取群G中的一个2-元素b，有b∈H．否则，对任意整数k≥1，b2k∉H，这与b是一个2-元素(存在某个正整数m使得b2m=1)矛盾．因此，H包含了G的所有2-元素，则对每个g∈G，g-1Hg包含了G中所有的2-元素，即Core(G,H)包含了G的所有Sylow 2-子群．

充分性:假设Core(G,H)包含了G所有的Sylow 2-子群．若a∉H且a2∈H.设a的阶为m．若m是偶数，则可设m=2kt(k≥1且为整数，t>1且为奇整数)．由于at是G中的一个2-元素且a2∈H，可得at∈H，且at-1∈H，所以a∈H．同理，若m是奇数，则am=1∈H，且am-1∈H，所以a∈H.总之，在以上假设之下所得结论都与a∉H矛盾．因此a∈H当且仅当a2∈H，即H满足条件PC．

当H是正规子群时，由Core(G,H)=H可得到下面的推论3．

推论3 设G是一个群且H是群G的一个正规子群．H满足条件PC当且仅当H包含了G的所有的Sylow 2-子群．

一个正规子群包含所有的Sylow 2-子群当且仅当它在群中的指数是奇数．因此，可得下面的推论4．

推论4 指数为奇数的正规子群可作为凯莱图的完备码．

根据推论1和推论4可得到下面的推论5．

推论5 令G是一个奇数阶的有限群，则G的每个正规子群都是群G的凯莱图的完备码．

在文献[17]中存在和推论4以及推论5一致的结果，但这里给出了一个更为简洁的证明．从前面的讨论中可以得出，奇数阶群的正规子群，奇数阶的正规子群以及指数为奇数的正规子群均可作为凯莱图的完备码．偶数阶群的阶数和指数均为偶数的子群的情况还有待解决．而广义四元数群和广义二面体群是两类偶数阶群，下面讨论这两类群的子群完备码并找出这些群的所有可作为完备码的子群．

3 广义四元数群和广义二面体群的子群完备码

3.1 广义四元数群的子群完备码

定理2 令G=〈a,b|a2n=1,b2=a2n-1,b-1ab=a-1〉为阶是2n+1的广义四元数群,则群G的所有非平凡子群都不能作为群G的凯莱图的完备码．

证明取G的一个非平凡子群H，则H的阶为偶数，由于G有唯一的2阶元b2，所以b2∈H．假设H是G的某个凯莱图的完备码，由引理1可得H有一个陪集代表系T且T可作为群G的以子群H为完备码的凯莱图的广义凯莱子集，即T/H=(T/H)-1.又因为|T|=|G∶H|是偶数，则有b2∈TH，这与b2∈H矛盾．所以群G没有非平凡的子群可作为其凯莱图的完备码．

定理3 令G=〈a,b|a2n-1=1,b2=a2n-1m,b-1ab=a-1〉为阶是2n+1m(m为奇整数)的广义四元数群,则群G的奇数阶的非平凡子群可作为群G的凯莱图的完备码，偶数阶的非平凡子群可作为完备码当且仅当它在群G中的指数是奇数．

证明注意到b2为群G唯一的2阶元．取群G的非平凡子群H，若H的阶为奇数，则H是循环群〈a2n〉的子群．因此H是G的正规子群．由推论1可得H是G的完备码．

若H的阶为偶数，则b2∈H．假设H是G的某个凯莱图的完备码，则H在G中的指数是奇数．否则，H的任意的右陪集代表系除b2之外至少还应该有一个2阶元，这与群G有唯一的2阶元矛盾．相反，若H在G中的指数是奇数，则H〈a〉且am∈H．所以，H=(H∩〈a〉)〈b〉且H在G中的指数与H∩〈a〉在〈a〉中的指数相等．因为H∩〈a〉是〈a〉的正规子群，由推论4可知H∩〈a〉在〈a〉中有一个对逆封闭的右陪集代表系，记为则T也是H在G中的一个右陪集代表系．因此，H是凯莱图Cay(G,T{1})的完备码．综上，偶数阶的非平凡子群可作为完备码当且仅当它在群G中的指数是奇数．

3.2 广义二面体群的子群完备码

令G=〈a,b|a2n=1,b2=1,b-1ab=a-1+2n-1〉为阶是2n+1的广义二面体群．则若i是偶数，元素aib的阶为2，若i是奇数，元素aib的阶是4．

定理4 令G=〈a,b|a2n=1,b2=1,b-1ab=a-1+2n-1〉为阶是2n+1的广义二面体群，H是G的子群．

(1)假设H〈a〉．

(I) 若b∈H，则子群H可作为群G的完备码当且仅当H∩〈a〉≤〈a4〉．

(II) 若ab∈H，则子群H可作为群G的完备码当且仅当H=〈a2〉〈ab〉．

(2)假设H≤〈a〉．则子群H可作为群G的完备码当且仅当H=〈a〉．

证明(1) 假设H〈a〉,不失一般性我们可以假设b∈H或ab∈H．

若y=x2i+1，则x的阶是2.此时,H∩〈a〉=1，H=〈ab〉,因此x=a2n-1=(ab)2也在H中，这与x∈〈a〉H矛盾．所以Hx不存在形如x2i+1的二阶元．

若y=x2iabx，y的阶为2当且仅当〈x〉=〈a〉．这时，H=〈a2〉〈ab〉,显然{1,b}是H的一个对逆封闭的右陪集代表系，且H是Cay(G,{b})的完备码．

(2)假设H≤〈a〉．在这种情况下，H是G的正规子群．若H是〈a〉的非平凡正规子群，则存在一个元素x∈〈a〉H且x2∈H，因此H=〈x2〉．而Hx中每个元素的阶都与x相同，因此，Hx对逆封闭但是没有2阶元．这表明〈a〉的任意非平凡正规子群都不能作为G的完备码．而易得H=〈a〉时可作为完备码．因此，当H≤〈a〉时，H可作为完备码当且仅当H=〈a〉．