一类转动机器人的随机自适应轨迹跟踪

杨 存,崔明月

(烟台大学数学与信息科学学院,山东 烟台 264005)

随着人工智能技术的发展,机器人的应用不断渗透生活中的各个领域.机器人可以完成人类所不能完成的任务,在许多高危环境中都可以看到它们的身影.因此对机器人系统的研究吸引了越来越多学者的关注.在机器人动力学建模方面,文献[1-3]中有详细的阐述,主要利用拉格朗日力学建立如下模型:

其中,q∈n为广义坐标,M(q)∈n×n为广义质量矩阵,n×n为Coriolis矩阵,h(q)为势力,τ∈n为广义力.在机器人控制器设计方面,ISLAM等[4]基于输出反馈滑模控制方法对机械臂进行控制研究.对于单杆旋转机器人,LU等[5]设计了模糊PID控制器,其控制结果具有很高的鲁棒性.机器人模型中通常会含有一些未知参数,如抓取物体的质量未知,这时需要设计自适应控制器.对带有未知参数的平面柔性机械臂,MAOUCHE等[6]设计自适应跟踪控制器.SU等[7]研究的是电流未知的电机驱动的机器人模型.BRIDGES等[8]设计的自适应控制器解决了机电刚性连杆机器人模型中参数不确定的问题.利用分离原理,WANG[9]设计的自适应控制器实现了良好的轨迹跟踪.然而以上文献主要研究的是确定情形下的机器人控制问题.

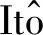
本文的主要工作:

(1) 如何合理地刻画随机干扰并将其引入到系统中是建模的难点.我们将随机干扰和力描述为随机加速度,它是一个随机过程.首先在确定情形下,通过拉格朗日力学的相关知识建立转动机器人模型.然后利用动静法,将环境的随机扰动转化为对力矩的随机干扰,从而得到转动机器人模型的随机拉格朗日方程.

(2) 抓取物体的质量和空气阻力未知增加了跟踪控制器设计的难度.首先将未知参数分离出来.然后设计自适应跟踪控制器使得闭环系统噪声到状态依概率实际稳定,通过设计调优参数使得跟踪误差收敛到零的任意小邻域内.最后仿真结果说明了策略的有效性.

符号说明:n表示实n维空间;+表示所有非负实数的集合;m×n的含义是m×n的实矩阵空间;K表示的是从+→+的过原点且严格递增的连续函数;KL表示+×+→+的所有函数β(s,t)的集合:对每一个固定的t是K类函数且对固定的s,当t→∞时递减到0;Ci表示i阶可导且导函数连续的空间;对于向量x,xT表示x的转置;|x|表示欧几里得范数;对于矩阵X,det(X)表示方阵的行列式;||X||F表示X的Frobenius范数,其表达式为||X||F=(tr{XXT})1/2,其中tr(·)表示方阵的迹,即主对角线上所有元素的和.

1 问题提出

本文所要研究的是如图1所示的转动机器人,其身体可以360°旋转,将身体简化为位于坐标原点O的竖直杆,机器人的前臂和后臂分别用2根杆表示,第i(i=1,2)根杆的长度和质量分别为li(单位m),mi(单位kg),g为系统所受的重力加速度,单位为m/s2.假设机器人在运动过程中会受到空气阻力的作用,每根杆的空气阻力系数为ki(i=1,2).在此模型中,参数m2,ki未知.ξ1,ξ2,ξ3分别表示O点在空间(X轴,Y轴,Z轴)3个方向的扰动加速度,在这里将其看作有色噪声.

在此模型中,选取广义坐标为qi(i=1,2),其中q1表示机器人后臂在平面内转动的角度,q2表示机器人前臂在竖直平面内摆动的角度,其单位为rad;ui表示作用于每根杆的力矩,其单位是N·m.

本文的主要目标:

(1)将随机干扰合理地引入到模型中建立转动机器人的随机拉格朗日方程.

(2)对于给定的期望轨迹qd(t)∈C2(2),设计一个自适应跟踪控制器使得输出q尽可能近地跟踪到参考信号qd,同时保证闭环系统的所有信号依概率有界.

2 系统建模

2.1 确定情形下建模

在确定情形下对转动机器人的建模,主要应用拉格朗日方程[18].选取转动角度q1,q2为广义坐标.在如图1所示的模型中,根据空间坐标系分别写出质点的自然坐标为

则系统动能为

其中q=(q1,q2)T,广义惯性矩阵为

取XOY面为零势能面,则系统势能为

V=-m2gl2cosq2.

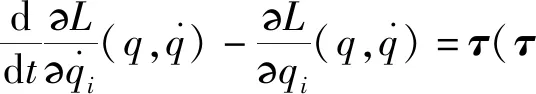
(1)

其中Coriolis矩阵为

其中ki(i=1,2)未知.则广义力

τ=ρ(v)+u,

其中u=(u1,u2)T.在确定性情形(ξi=0)下,系统的模型为

(2)

2.2 随机情形下建模

系统在作业过程中受到环境中随机振动的影响,假设ξi(i=1,2,3)分别表示空间中(X轴,Y轴,Z轴)的扰动加速度,在这里可以看作有色噪声.根据力学等价原理[19]和动静法来对转动机器人建立随机模型.将有色噪声看作对控制u的干扰,即加入随机等价力.如图2(a)所示,在O点分解ξ1,ξ2得到

ao1=ξ1cosq1+ξ2sinq1,

ao2=ξ1sinq1+ξ2cosq1,

如图2(b)所示,在A点分解ao1,ξ3得到

因此,作用于第i根杆的等价随机力矩为

(3)

其中,ξ=(ξ1,ξ2,ξ3)T,

用u+Λ(q)ξ替换系统(2)中的u得到转动机器人模型的随机动力学方程为

(4)

2.3 模型的性质

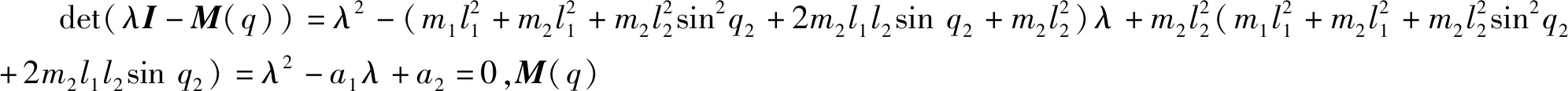
因此,

0<λ1I2×2≤M(q)≤λ2I2×2.

(5)

(6)

3 自适应跟踪控制器

为了控制器设计,将式(4)写成如下准下三角结构形式

(7)

假设A1 随机过程ξ(t)为Ft适应过程且分段连续,存在一个常数D>0,使得

(8)

由于系统中含有未知参数m2和未知的空气阻尼系数ki,在控制器设计之前,需对含未知参数的项进行处理.在耗散项中,

其中θ=(k1,k2)T未知.对于含有m2的项,处理可得

3.1 自适应跟踪控制器设计

下面进行自适应控制器的设计.首先引入坐标变换

z1=q-qd,

(9)

其中α=-c1z1(c1>0),结合式(7)得

(10)

其中

选取Lyapunov函数

(11)

对式(11)求导并根据式(10)和性质(6)可得

(12)

根据Young不等式,有

(13)

其中常数d1>0为设计参数.将式(13)代入式(12),整理得

(14)

取自适应律

(15)

取控制律

(16)

其中常数c2>0.因此

(17)

最后可得闭环系统

(18)

3.2 稳定性分析

定理1 对于系统(4)和一个有界的给定参考信号qd,设计控制器(16)使得

(1) 闭环系统(18)是NSpS-P,即对任意的ε>0,存在KL类函数β(·,·)和K类函数γ(·)使得对t∈[t0,∞)和x0∈n有

P(|x(t)|≤β(|x0|,t-t0)+γ(δ1D+δ2))≥1-ε.

(19)

(2) 闭环系统所有信号依概率有界,并且跟踪误差z1=q-qd满足

(20)

其中不等式右边可通过调节合适的参数使得足够小.

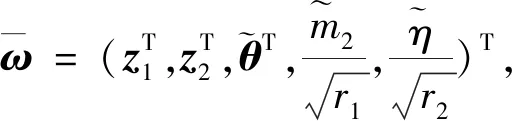
(21)

(22)

(23)

4 仿真实验

为了验证自适应控制器的合理性,需要对系统(4)进行仿真.首先给出参考信号qd=[0.5sint,0.5cost]T,选取函数的初始值为q(0)=[0.5,-0.3]T,θ(0)=[0,0]T,m2(0)=η(0)=0;系统的参数为m1=0.5,m2=0.1,g=9.8,l1=1,l2=1.2;设计参数为c1=1.2,c2=1.4,d1=1,σ1=0.3,σ2=0.6,σ3=0.3,r1=0.6,r2=0.7,k1=0.4,k2=0.2,Γ=I2×2为单位矩阵;随机干扰ξi(t)满足

其中pi>0是一个常数,w(t)∈是一个零均值白噪声而且其中Ai>0为噪声功率,tc为采样时间.选取A1= 0.2,A2=0.2,A3=0.1,tc=0.1,p1=2,p2=2,p3=2.最后的仿真结果如图3所示.

5 结 论

本文考虑了一类空间转动机器人在随机振动环境下的自适应跟踪控制问题.基于拉格朗日力学的相关知识建立转动机器人模型的随机方程,然后设计自适应跟踪控制器使得跟踪误差的均方趋于零,最后的仿真实验说明了控制器设计的合理性.还有一些其他问题需要考虑,例如如何简化控制器,在速度不可测时设计输出反馈控制器.