某近现代文物建筑修缮加固前后动力响应测试分析

XIE Yongjian

0 引言

采用环境激励法对受损房屋进行动力测试，从而得到结构的动力性能参数(自振频率、阻尼比)，通过同类结构相比，分析结构固有频率和阻尼变化，得出结构刚度退化程度、地震对结构的损伤程度，在房屋安全鉴定中证明可行[1-2]。本文将以某近现代重点文物建筑为研究对象，开展结构修缮加固前后的动力响应实测研究，对比修缮加固施工前后固有频率和阻尼比的变化，为今后类似结构的防止工业振动加固或既有建筑结构的损伤识别积累经验。

1 房屋修缮加固概况

某近现代文物建筑始建于1922年，坐南朝北，原为仿西式巴洛克风格的4层（局部5层）砖木结构建筑，后经多次修缮，内部改为框架结构。建筑平面呈“回”字形布置，内设天井，主体4层，前部屋顶设两层塔楼，建筑总高度约为21.6 m，建筑面积4 245 m2（图1、2）。该建筑一～三层均为陈列展厅，四层为办公区域。其中，建筑底层层高4.5 m，二、三层层高均为3.4 m，四层层高3.3 m。房屋原有墙体基础采用三合土垫层、砖砌大放脚基础；后来加固时，加固设计的框架柱采用钢筋混凝土条形基础，局部采用独立基础，房屋基础埋深约1.75 m。总体上，房屋的主体结构基本为内部钢筋混凝土框架和局部砖墙承重，外围护砖墙基本为自承重墙的混合结构体系。

图1 某近现代文物建筑立面图

本次修缮加固主要针对部分结构承载力不足的梁柱进行加固。其中，柱的加固方式主要采用加大截面和外包型钢两种，其刚度变化较大；梁的加固主要采用混凝土置换、粘贴碳纤维、外包型钢等3种方式，其截面形状大小没有明显改变，刚度变化小。此外，对建筑结构老化损伤进行修缮，如采用压力灌浆对墙体裂缝进行修缮，凿除混凝土构件表面酥松混凝土，采用高强度的灌浆料置换等。房屋的结构平面布置如图3、4所示，其中，柱的加固情况详见图中示例。

2 测试方案

2.1 测试工况设计

加固前，对房屋的初始状况先进行1组模态测试；加固后，再进行2组独立模态测试(第1组和第2组分别在不同日期夜间相对安静的情况下测试)，模态测试工况如表1所示。通过比较加固后第1组和第2组的模态参数变化量，验证模态参数的一致性和稳定性，证明本文所采取的方法能反映结构刚度的实际变化测试要求；同时，比较加固前后模态参数的变化，分析结构加固对固有频率和阻尼比的影响。

2.2 仪器设备

图2 某近现代文物建筑典型平面图

图3 某近现代文物建筑一～三层结构平面图

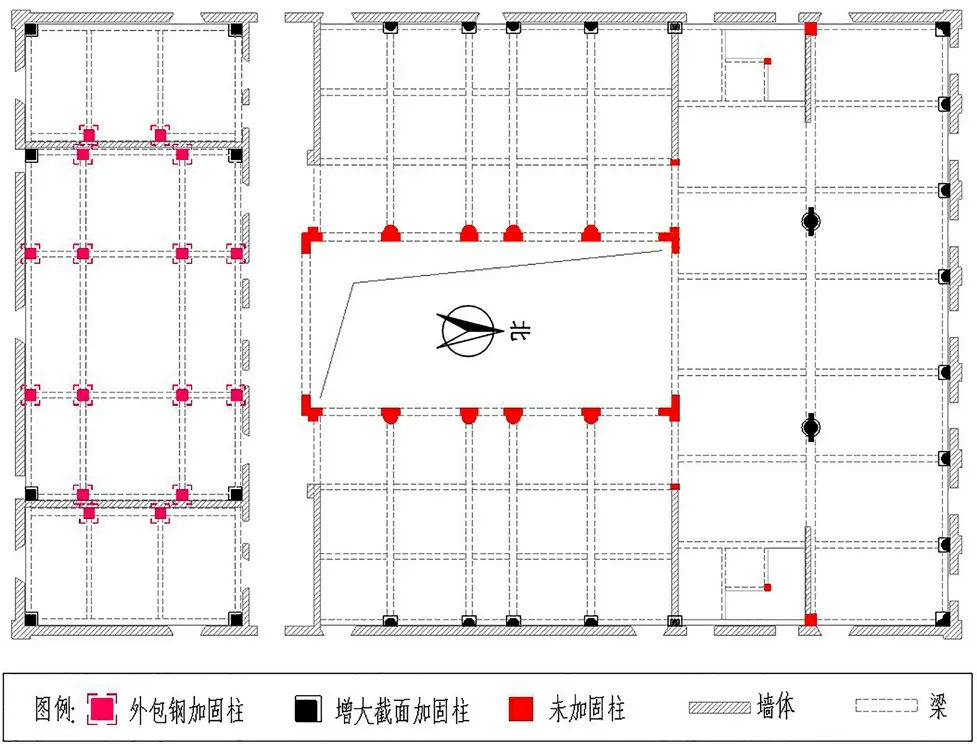
图4 某近现代文物建筑四层结构平面图

动力实测设备采用941B型拾振器接收速度信号，经941型16线放大器放大后，送NI 9220采集卡采集，由北京东方振动和噪声技术研究所DASP采集分析软件进行存储及数据处理，动力测试系统如图5所示。考虑到本建筑为多层，结构平面布置较为规则，故主要研究建筑平动的第一阶振型。

2.3 测点布置

平动模态的测点宜布置在建筑物的刚度中心，其目的是为了让传感器尽量仅接收到平移振动信号而屏蔽掉扭转振动信号，从而在做数据分析处理时，便于识别平移振动信号。当受现场试验条件的限制，不可能在建筑物的刚度中心安放传感器时，要尽可能地靠近刚度中心，使扭转振动信号尽可能地小，突出平移振动信号。

本工程中，鉴于建筑呈“回”字型，内部为天井，故分别在二～四层楼面及屋面天井一侧靠近中心区域各布置了3个水平振动传感器（共12个），且3种工况的测点布置位置均一致（图6～8）。

在布置传感器时，每个方向上的传感器测试方向尽量一致，在各楼层上测点的平面位置也尽量一致，使传感器能稳固地放在结构层上，以避免受到建筑装修的影响。另外，传感器附近避免磁场干扰及局部振动。

表1 模态测试工况

图5 动力测试系统

3 数据采集

为避免人员干扰，每个工况均在夜间安静时段进行数据采集，采集时间均为2 h，采集参数为速度，采用频率均为204.8 Hz。

对图9所示的各工况振动时域数据去直流分量，并进行加汉宁窗的快速傅里叶变换，得到如图10所示的振动速度频谱曲线。由图9可知：加固前顶层水平方向的振动主频为3.02～3.32 Hz，加固后顶层水平方向的振动主频为3.60～3.80 Hz；加固措施使得结构水平方向振动主频增加约16%。本节数据主要反映单点测试数据的振动响应，而研究建筑整体响应需要采用模态分析方法分析固有频率和阻尼比等参数特性。

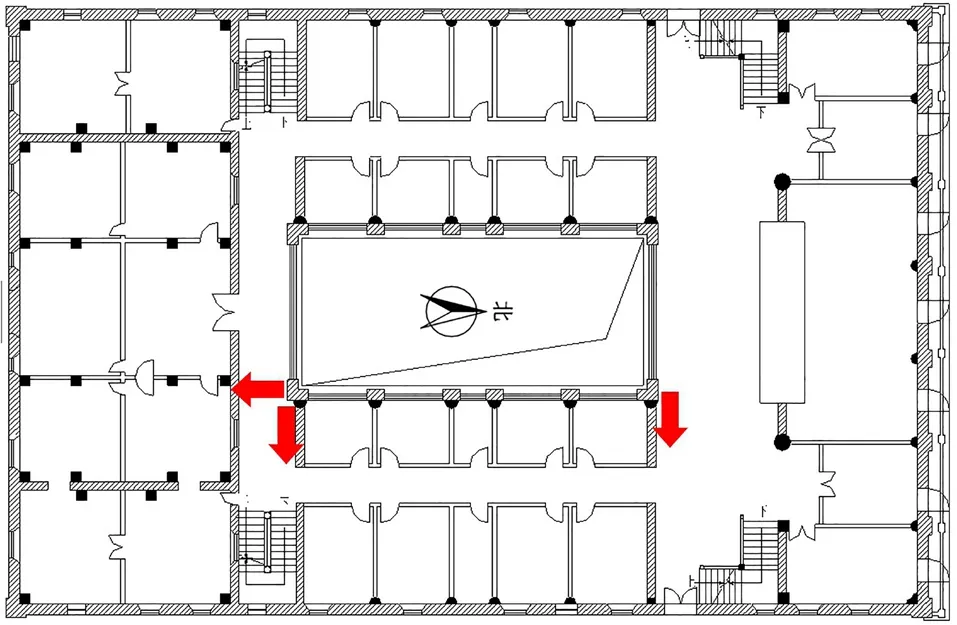
图6 标准层测点布置示意图

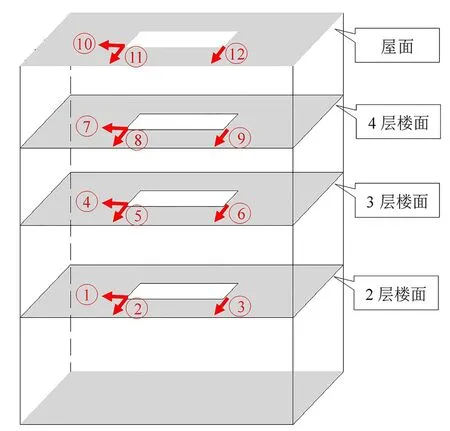
图7 各层测点布置示意图

图8 传感器布置典型照片

4 模态分析

4.1 建立模型

本建筑平面结构呈“回”字型，中间有一矩形天井。利用模态分析软件（Coinv DASP V10）建立模型，共包括20个节点。模型中，每个节点为3个自由度，故总共为60个自由度。模型建立完毕后，需要对每一个节点进行自由度约束。这里的约束和力学中讲的约束不同，并不是指的固支、简支等边界条件，而是将建立的结构模型和采集的数据一一对应，这样在模态分析中才能按照数据的特性去运动，才能形成模态振型。

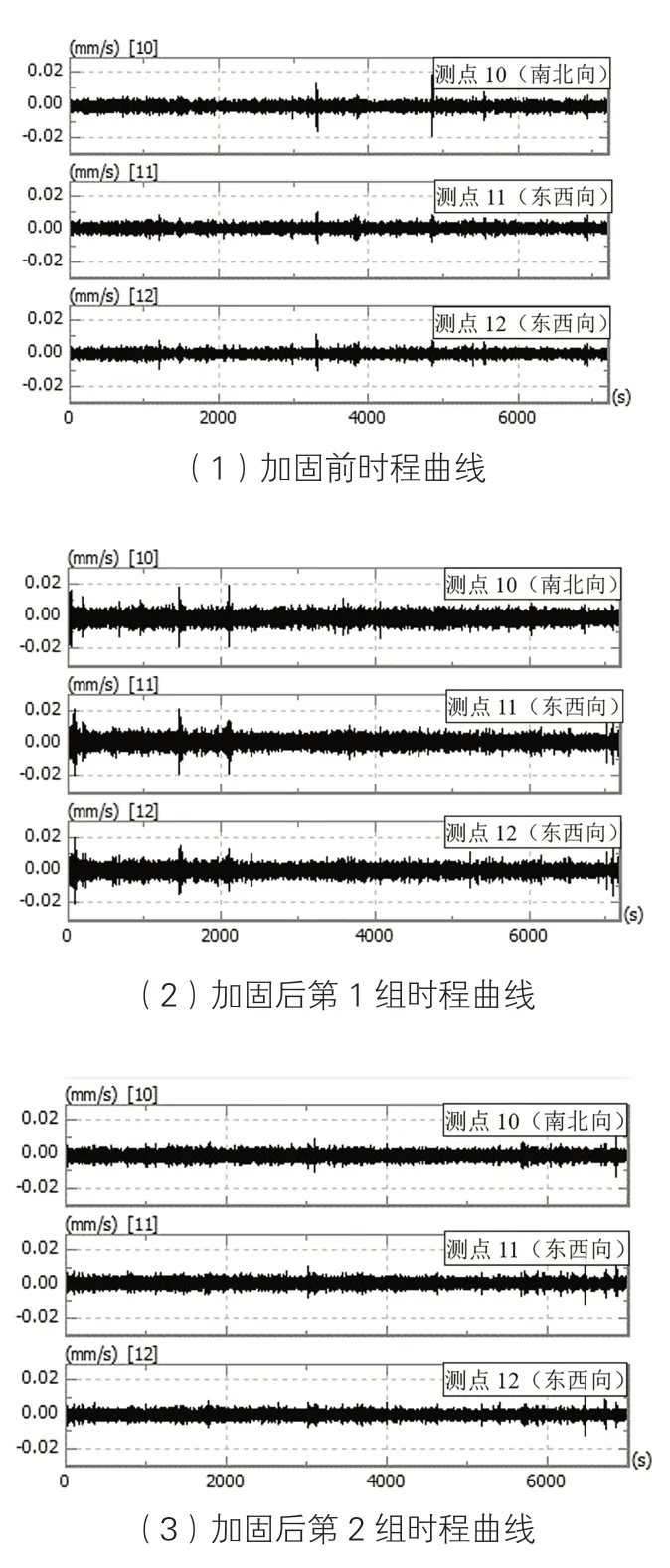
图9 各工况典型速度时程曲线图

为了得到本次关心的水平振动模态，考虑到本次测点的数量，需要对模型约束作以下假定：①所有节点铅垂方向的自由度均为零；②假定地面节点各方向的自由度为零；③同一楼层中，同一轴线上的两个测点在相同方向的自由度相同。

将测量数据对应输入到结构模型中，其模型及数据约束如图11所示。

4.2 模态拟合

图10 各工况典型频谱曲线图

图11 模型建立及数据约束

利用模态分析软件（Coinv DASP V10）选择合适的方法进行模态拟合，主要可以分为时域法和频域法。本次模态拟合采用时域法中的随机子空间法（SSI），以线性的离散状态空间方程为基本模型，将输入项和噪声项合并假定为白噪声，并以此为基础，利用白噪声的统计特性进行计算，得到卡尔曼滤波状态序列，再应用最小二乘计算系统矩阵，完成识别过程。

4.3 测试结果

通过模态分析，可以得到结构的固有频率和阻尼比。

（1）比较加固后两组测试数据的固有频率及阻尼比（表2）。从表2可以看出，结构加固后，两组不同测试数据模态分析得到的固有频率和阻尼比都非常接近，第2组数据相对于第1组数据，南北方向一阶平动固有频率相差0.7%，阻尼比相差5.6%；东西向一阶平动固有频率基本相同，阻尼比相差5.3%。这说明结构的固有频率测试值一致性非常好，阻尼比差别不大。

（2）对比加固前和加固后的模态分析数据（表3），加固后结构南北方向和东西方向一阶平动固有频率两组数据的平均值相比加固前分别增加了20.1%和13.1%，阻尼比相比加固前分别增加了25%和42.3%，说明加固前后的动力参数（固有频率、阻尼比）发生了较大改变。

表2 结构加固后两组固有频率与阻尼比

表3 结构加固前后固有频率与阻尼比

4.4 分析

国外文献［1］认为，当固有频率改变5%以上时，能够比较肯定地认为结构出现了损伤。但是，本工程模态分析结果表明，通过对既有建筑进行结构加固，固有频率的改变比建筑物自身劣化引起的改变更加明显。通常情况下，结构的刚度及填充墙的分布和质量均会对固有频率存在影响，而本项目填充墙等非结构构件相对于加固前没有明显改变，其固有频率的改变主要是由结构加固导致的。

对于阻尼比的改变，其原因更加复杂，文献［2］指出，一般情况下，结构的阻尼比随频率的增加而增加；且非承重构件的数量和材料也是影响结构阻尼比的因素，如较多填充墙的宾馆和宿舍就比较少隔断的办公楼阻尼大。文献［3］指出，建筑装饰特别是外部玻璃幕墙对结构的阻尼比影响很大。可见在今后的结构损伤识别或振动控制工程中，通过固有频率的改变是可行的。

5 结语

本项目通过对某近现代建筑结构加固前后振动模态分析，得出建筑固有频率和阻尼比的变化幅值，可为今后类似近现代文物建筑防止工业振动加固和损伤识别提供参考。