单通道控制旋转弹系统动力学建模与Hopf分岔
许艳丽,岳宝增,赵良玉
(北京理工大学宇航学院, 北京 100081)
0 引 言
旋转弹是一类在飞行前进过程中弹体绕自身纵轴连续滚转的飞行器,具有简化控制系统组成、减少制造误差影响、提高突防能力等诸多优势[1]。然而,弹体的自旋同时也会带来新的问题,如马格努斯效应[2]、陀螺效应[3]下的以不收敛锥形运动所表现出动态失稳现象,会对导弹的射击精度及射程指标产生不可忽略的影响[4-5],许多学者针对此类问题进行了研究。文献[6]创造性地在非旋转弹体坐标系下建立了旋转弹的角运动动力学模型,推导了弹体角运动的充要稳定性条件,并首次提出了陀螺稳定与动态稳定的判定准则。文献[7]针对高攻角情形下的旋转弹无控飞行,考虑了更高阶的非线性偏航力矩系数,深入研究了旋转弹的“转速闭锁”和“灾变偏航”问题。文献[8]针对旋转对称导弹自旋偏航闭锁的非线性模型,分析了非线性气动系数对自旋偏航闭锁的影响,并建立了非线性气动系数的优化模型以获得所需的闭锁运动,实现其在弹箭设计中的应用。文献[9]针对柔性旋转弹的动力学问题,在考虑转速的作用下,建立了计入陀螺力矩及随动推力影响的运动方程,并分析了系统的动力稳定性问题。
随着现代战争对常规兵器要求的不断提高,带有控制系统的旋转弹得到了越来越广泛的应用。文献[1,10-11]系统研究了带有制导控制系统的旋转弹动态稳定性问题,尤其是在旋转弹控制耦合和控制系统稳定性分析及控制系统设计方面取得了重大进展。与一般导弹所采用的双通道(俯仰、偏航)控制方式及三通道(俯仰、偏航、滚转)控制方式不同,带有一对舵面的旋转弹可通过弹体自旋,实现单一的控制通道对俯仰与偏航通道的操纵。国内外对于该类系统的数值气动分析、系统动力学建模、控制器设计等方面均开展了相关研究[12-14]。但对于表现出大攻角的旋转弹系统的建模及非线性动力学特性的研究涉及较少,还有待进一步发展与完善。
随着非线性动力学理论和方法的不断发展,其在飞行器及航天器的非线性动态问题分析中已得到越来越广泛的应用[15-20]。文献[15-17]将延拓算法和分岔理论应用到飞行器在大攻角飞行情况下的纵向与横侧向失稳问题的研究中。对各类飞行器的非线性运动进行了系统的分析,并提出相应控制方法。文献[18]运用了中心流形定理的局部降维,分析了轻微不对称旋转弹的局部分岔和稳定性,同时采用数值方法研究了旋转弹的全局分岔,定量分析了旋转弹系统的动态特性。文献[19]采用中心流形定理并结合规范形理论,以空气密度作为分岔参数,对火箭弹非线性角运动的分岔特性进行了分析。文献[20]通过CFD/RBD方法,研究了纵向不稳定弹的自由飞行动力学特性,同时引入非线性理论对导弹动力学系统展开了鞍节分岔分析,并进一步探讨了导弹失稳后的非线性行为。因此,分岔方法已经成为复杂飞行动力学非线性领域中的一个非常流行且有力的工具。然而,以上研究结果基本上采用的是数值方法对旋转弹的动态特性进行的分析,还没有给出旋转弹发生分岔的一般解析式条件。
基于单通道控制的低通滤波特性,本文建立了具有面对称性旋转弹系统的复系数动力学模型。基于复系数方程的稳定性理论推导了面对称性旋转弹的稳定性条件,研究了系统的局部分岔特性,探索了系统关键参数对稳定条件及非线性动力学特性的影响规律,并进一步发现了系统耦合动力学模型所表现出的拟周期运动及混沌运动在内的复杂非线性动力学行为。本文的研究结果对旋转弹的控制参数及结构参数设计具有一定的指导意义。
1 单通道控制旋转弹系统动力学建模
旋转弹可利用一对鸭舵同时控制俯仰和偏航通道,不同于两对鸭舵的控制,一对舵片偏转的气动效应只具有面对称性而不再具备滚转对称性[12]。为了能准确描述单通道旋转弹所表现出来的旋转不对称性,先将旋转弹动力学模型建立在弹体坐标系下随后将其转换到准弹体坐标系下。如图1与图2所示,O为弹体质心,Ci(i=1,2)为两鸭舵的压心;OBxByBzB是弹体坐标系,简记为坐标系-1;ONxNyNzN是准弹体坐标系;OVxVyVzV是速度坐标系;OCixCiyCizCi(i=1,2)为鸭舵坐标系,分别简记为坐标系-2与坐标系-3,其相应的基矢量定义为iCi,jCi和kCi。
注1. 原点OB,ON及OV与质心O重合。

图1 坐标转换示意图Fig.1 Coordinate transformation diagram
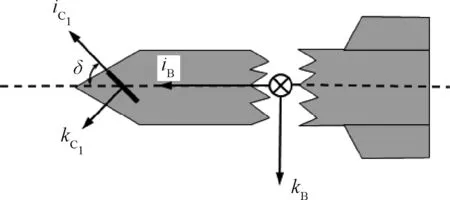
图2 弹体坐标系与鸭舵坐标系的坐标转换示意图Fig.2 Coordinate transformation in OBxByBzB and C1xC1yC1zC1
由弹道理论,弹体坐标系OBxByBzB下的横向动力学方程可表示为:
(1)

俯仰与偏航通道的力与力矩包括气动力与控制力及相应产生的气动力矩,其中弹体系下的气动力与气动力矩表示成如下形式[1,12]:
(2)
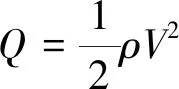
注2. 文中规定j(·)(j=1,2,3)表示任一矢量在相应序号坐标系下的坐标矩阵。
考虑鸭舵舵面偏转引起的弹体气动载荷的变化,需将鸭舵的舵偏角转换为全攻角,图2是鸭舵的结构示意图。两片鸭舵压心在弹体系下的坐标矩阵分别为[12]:
(3)
式中:Δxc与Δyc为在iB和jB方向上鸭舵的压心到质心的距离。
由速度合成定理,鸭舵压心的速度矢量在弹体坐标系下的坐标矩阵可表示为:
(4)
式中:[·]×表示为矢量叉乘矩阵,且VO表示弹体质心相对于惯性坐标系的速度矢量,其坐标矩阵为1VO=[u,v,w]T,ω为弹体坐标系相对于惯性坐标系的角速度矢量,其坐标矩阵为1ω=[p,q,r]T。
由图2可知,弹体坐标系与鸭舵坐标系的转换关系矩阵为:
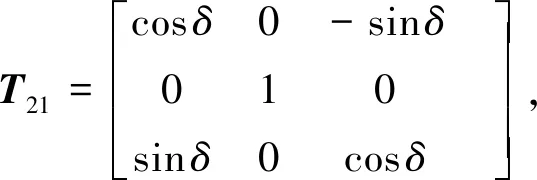
(5)
则鸭舵坐标系下的压心速度可表示为:
2VC1=T211VC1,3VC2=T311VC2
(6)
进而求得鸭舵坐标系下由鸭舵偏转引起的气动力为:
(7)
式中:CxC为鸭舵面的轴向阻力系数,CNC为舵面法向力系数对舵偏角的偏导数,且
(8)
通过式(5)与(7),可得鸭舵产生的力与力矩在弹体系下的坐标矩阵为:
(9)
将式(2)和(9)在yB与zB方向的坐标分量代入式(1),并将其表达为如下矩阵形式:
(10)
式中:
(11)
由图1可知,只考虑yB与zB方向的弹体坐标系与准弹体坐标系的转换矩阵为:

(12)
则有
(13)
式中:“~”表示为在准弹体坐标系下。

(14)
式中:


(15)
且旋转弹的复横向角速度表示为:

(16)
式中:i表示虚数单位。
将式(15)和(16)对s求导,可以得到如下的关系式:

(17)
且:
(18)
联立式(14)~(18),可求得复数形式的质心横向运动方程与绕质心转动方程:
(19)
在考虑大攻角引起的非线性因素情况下,静力矩系数导数CMα,马格努斯力矩系数导数CMpα,阻尼力矩系数导数CMq可分别表示为[1]:
(20)
将式(20)代入式(19),联立求解得复数形式的角运动方程:
(21)
式中:
(22)
对式(21)中的变量做如下变换:
τ=[|M0|/κ]1/2s,
则方程(21)整理如下:
(23)

2 旋转弹系统局部稳定性研究
对于系统(23),相对应的齐次复数方程与平衡点处的二阶复数特征方程为:

(24)
(25)
根据复数方程的稳定性判据[1],由式(25)决定的单通道旋转弹系统的稳定条件为:
(26)
引入陀螺稳定因子与动态稳定因子[1,6]:
(27)
则稳定性条件(26)可整理为:
(28)
以Sd为横坐标,1/Sg为纵坐标,由稳定性条件(28)即可获得图3所示的动稳定性边界。如图所示,1/Sg=1以下的区域满足陀螺稳定条件,为陀螺稳定域;坐标轴Sd以下的区域为静稳定区域;且当Sd在区间(-1, 1)范围内,静稳定旋转弹一定是动态稳定的,而在(-1, 1)区域之外,静稳定弹的转速、气动参数等需满足条件(28)才能使其动态稳定。而静不稳定旋转弹当Sd在(-1, 1)范围内可通过提高转速了来达到动态稳定,但在(-1, 1) 之外企图通过提高转速使其动态稳定已无法实现。因此,由式(27)并结合图3可知,马格努斯力矩过大或者阻尼力矩过小均使得旋转弹系统难以达到动态稳定。马格努斯力矩过大,Sd<-1;阻尼力矩过小,Sd>1。

图3 旋转弹的稳定性边界Fig.3 The dynamic stability boundary of a spinning projectile


图4 静稳定旋转弹的动态稳定域Fig.4 The dynamic stability region of a static spinning projectile
图4给出了转速、静力矩、马格努斯力矩与阻尼力矩之比的变化对旋转弹系统稳定性的影响,其中有颜色部分为稳定区域,由图可知,静力矩的减少会降低转速的动态稳定性区域,即考虑鸭舵带来的非对称影响计算得到的转速范围要比不考虑非对称计算得到的转速范围小,若按照旋转对称求得的稳定性条件设计旋转弹,可能会存在一定转速范围的偏差,造成旋转弹系统的失稳现象。
3 旋转弹系统Hopf分岔分析
根据非线性系统的分岔理论[21],对旋转弹系统进行Hopf分岔分析,解析推导旋转弹系统Hopf分岔发生的条件,并通过计算第一Lyapunov系数给出极限环稳定性的判定准则。
(29)
F(x)=
则式(29)的特征多项式为:
(30)
假设系统(29)的特征方程有纯虚根λ1,2=±iω, (ω>0),将其代入式(30)所对应的特征方程,分离实部与虚部后,最终得到的旋转弹系统分别在不同参数下发生Hopf分岔的解析式条件为:
对静不稳定旋转弹,有
(31)

对静稳定旋转弹,有
(32)

注3. 文中( )u表示静不稳定弹,( )s表示静稳定弹,( )h表示发生Hopf分岔的临界值。
对静不稳定旋转弹,有
(33)

对静稳定旋转弹,有
(34)

对静不稳定旋转弹,有
(35)
对静稳定旋转弹,有
(36)


证. 通过式(31)~(36)可知,系统(29)存在一对纯虚根,在不同参数下,它们满足:

则对于静不稳定弹,有:

(j=1,2);
式中:
(j=1,2)。
对静稳定弹,有:

(j=1,2);
式中:
(j=1,2)。

为了分析Hopf分岔的方向,接下来解析推导系统(29)在中心流形上的第一Lyapunov系数,以检测Hopf分岔周期解的稳定性。
(37)
式中:
系统(29)只含有三次非线性项。因此由两个向量x=(x1,x2,x3,x4)∈R4与y=(y1,y2,y3,y4)∈R4定义的双线性函数B(x,y)≡0;由三个向量x,y及z=(z1,z2,z3,z4)∈R4定义的三线性函数C(x,y,z)可表示为:
(38)
通过式(37)和(38)可得到


(39)

(40)
(41)
(42)
(43)
(44)
(45)
式中:j=1,2。
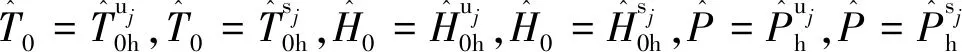
4 数值仿真与结果分析
为了验证上述旋转弹系统的动态稳定性条件及Hopf分岔发生条件的正确性与有效性,以下将采用数值方法研究马格努斯效应对旋转弹系统分岔特性的影响规律。利用时间历程图、相图、分岔图等探讨旋转弹动力学模型所表现出的复杂非线性动力学行为,以揭示旋转弹系统锥形运动的形态,并对其进行预测。

仿真过程中,要将其转换为弹体的攻角与侧滑角。由图1可知,弹体坐标系与速度坐标系的转换矩阵为:
(46)
则攻角与侧滑角可计算为:
(47)


图5 旋转弹系统的分叉图Fig.5 Bifurcation diagram of rolling projectile

图6 旋转弹系统的收敛运动Fig.6 Convergent motion of rolling projectile

图7 旋转弹系统的极限环运动Fig.7 Limit cycle motion of rolling projectile
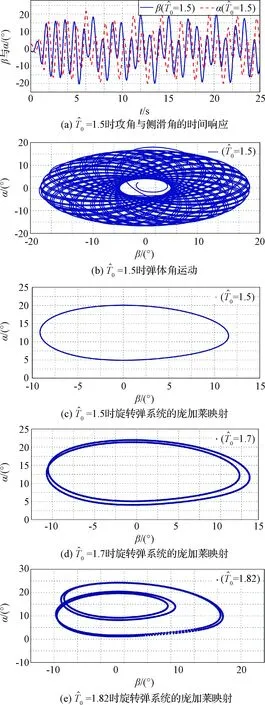
图8 旋转弹系统的拟周期运动Fig.8 Quasi periodic motion of rolling projectile

图9 旋转弹系统的混沌运动Fig.9 Chaotic motion of rolling projectile
图9(b)表明,两个不同初始条件的响应在10 s左右出现了差异,体现了混沌运动对初始条件敏感性。这些结果均证明了旋转弹锥形运动形态的多样性。
通过数值模拟可以发现,文中所建立的判断条件可以很好地预测旋转弹不收敛锥形运动的临界参数值,为非线性旋转弹系统的控制与结构设计提供了理论参考依据。研究表明为了保证旋转弹锥形运动的稳定性,可通过对系统引入气动参数以及结构参数,从而预测锥形运动的形式并确立其发生的条件,由此改进控制设计及结构设计以避免旋转弹运动的失稳。
5 结 论
本文建立了适应于处理大攻角运动的具有面对称性的非线性旋转弹动力学模型;推导了单通道控制旋转弹系统的稳定性条件及Hopf分岔条件,并给出了Hopf分岔发生所产生极限环的稳定性定理。文中给出的仿真结果证明了该条件的正确性与有效性。本文的研究结果还揭示了旋转弹锥形运动的多种表现形态,其中包括收敛的锥形运动、周期运动、拟周期运动与混沌运动。通过文本的研究结果,可以对旋转弹系统锥形运动形态发生的可能性及发生的条件做出预先判定,对旋转弹系统的控制设计及结构设计具有指导意义。

