一种运载火箭时变结构模态参数辨识的确定性演化方法
余 磊,刘 莉,2,崔 颖,岳振江,康 杰
(1. 北京理工大学宇航学院,北京 100081; 2. 北京理工大学飞行器动力学与控制教育部重点实验室,北京 100081)
0 引 言
运载火箭的仅输出时变结构模态参数辨识是航空航天工程领域的关键技术。运载火箭在工作状态下由于构型变化、模块化结构调整、载荷工况变化等过程,使得自身成为变结构、变质量、变参数的典型时变结构,获取结构的模态参数等动力学特性对于实现高精度控制起着关键作用,并直接影响复杂空间任务的顺利完成。
运载火箭的时变特性体现在微分方程系数中[1],并进一步反映在振动响应信号中,即时变结构的振动响应信号具有非平稳特性[2]。针对非平稳信号的辨识方法主要分为时域和频域,其中时域辨识方法直接以时域信号为基础进行模态参数辨识,物理概念更为清晰。时域辨识方法又分为基于状态空间的辨识方法[3-5]和基于时间序列的辨识方法,其中时变自回归滑动平均模型(Time-varying autoregressive moving average, TARMA)是时域仅输出辨识模型,作为一种参数化辨识模型,TARMA模型具有许多优点[6]:1)表达的简约性;2)更高的精度;3)更好的时变动态特性的跟踪能力;4)更高的分辨率;5)更好的灵活性。Spiridonakos等[7]根据TARMA模型的时变系数的演化形式不同,分为三类:无结构化、随机结构化和确定性结构化。
确定性结构化的时变系数演化形式即是将TARMA模型的时变系数用一组基函数进行展开,进而将时变系数转换为投影空间中的时不变投影系数,选择合适的基函数可以提高辨识精度。这类方法统称为泛函序列(Functional series,FS)TARMA模型。Rao[8]对TARMA模型的时变系数进行展开,基于时间多项式首次提出了FS-TAR模型。Mendel等[9]对一般的泛函时间序列模型进行了研究,讨论了时变系数的快变与慢变,建立了相关的理论基础。Liporace[10]基于任意阶多项式对FS-TAR模型的时变系数进行展开,并将模型应用于语音分析。Grenier[11]将FS-TAR模型首次拓展到FS-TARMA模型,并从数学上证明了FS-TARMA模型的存在性和唯一性。Walter等[12]研究了模型参数估计的精度与基函数类型的关系,并指出足够阶数的任意函数簇能以任意精度逼近时变系数。Zou等[13]采用了Walsh函数,对分段时变系数进行了展开。目前,多种多样的基函数被用于描述FS-TARMA模型的时变系数,如勒让德多项式、切比雪夫多项式[14]、雅克比多项式[15]、傅里叶级数[16-17]、B样条、无网格形函数[18]等。不同基函数所适应的问题各不相同,如勒让德多项式、傅里叶级数适应于慢变/长周期信号,B样条适应快变/慢变信号,无网格形函数适应快变信号。
小波方法因具有“数学放大镜”的作用,近年来也被频繁应用于频域模态参数辨识方法中。文献[19-20]将小波变换应用于脉冲响应函数提取和频率响应的估计,给出了响应的模态参数辨识方法。Staszewski等[21]基于小波变换将传统频率响应函数拓展到时频域,利用时间平均法提高了信噪比。Dziedziech等[22]进一步将该方法应用于频率突变系统,结果表明,小波函数的多分辨率特性能够在频率突变处很好的拟合,得到了更为光滑的时频分布图。小波方法对快变信号的良好适应性,在时频域/频域模态参数辨识方法上得到了广泛应用[23-24],却鲜有在时域仅输出模态参数辨识方法上的应用。
本文针对运载火箭运行工况下的质量变化特性,在确定性演化方法上,利用小波函数能够较好地反映信号局部细节的特点,选择墨西哥帽小波函数作为TARMA模型时变系数泛函空间基底,构建了基于小波基的FS-TARMA模型。利用分布解耦思想以及TARMA模型与无限阶截断模型相等价的原理,发展了两步最小二乘法对估计过程进行解耦,得到了时变系数的解耦估计。通过运载火箭时变有限元模型验证了提出的墨西哥帽小波基FS-TARMA方法具有良好的辨识精度与时变跟踪能力。
1 TARMA模型
TARMA模型是基于非平稳时间序列建立起来的离散模型,具有随机差分方程的形式,不仅可揭示动态数据本身的结构和规律,还可定量地了解观测数据之间的线性相关性,是解决动力学第一类反问题的有效工具。令na和nc分别表示AR阶数和MA阶数,TARMA(na,nc)模型可写为如下形式。
(1)
式中:x[t]∈Rk×1表示离散的非平稳振动信号,e[t]∈Rk×1满足均值为零且协方差为Σ[t]∈Rk×k的正态分布,Ai[t]和Ci[t]分别表示TARMA模型的时变AR和MA系数矩阵。
TARMA模型总是将输入信号假设为白噪声,因此保证了模型所表示的等价系统的固有特性包含了真实物理系统的固有特性,而没有丢失信息。在实际应用中当输入信号不可知时,白噪声激励假设是一种简单易行的方式,解决了系统辨识问题中输入信号未知时的困难,因此TARMA模型被广泛地应用于仅输出模态参数辨识领域。
TARMA模型“时间冻结”模态参数可以通过在每一时刻求解如下特征值问题[25]获得

(2)
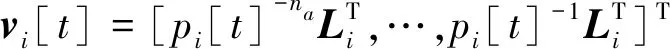

(3)
TARMA模型“时间冻结”固有频率和阻尼比为
(4)
2 TARMA模型的时变系数确定性演化方法
2.1 基于墨西哥帽小波基的TARMA模型
对于小波展开,可构造一个两参数系统,使得
(5)
其中,j和d为整数指标,ρj,d(t)是小波基函数,通常形成一组正交基。展开的系数集aj,d称为f(t)的离散小波变换。采用墨西哥帽小波函数作为基本小波,即母小波,对其进行二进尺度变换和时间轴上的平移,为方便运算,记小波基最大尺度因子等于时间基函数最大维数,可得其小波基为
(6)
其中,j=0,1,…,m为时间基函数的展开维数,m为最大维数;平移因子d=0,1,…,2j-1。当尺度因子j=0,1,…,m时,ρl,d(t)的伸缩即能拟合慢变和快变的时变系数,从而能够覆盖低频到高频的整个频带。则TARMA模型的时变AR系数矩阵和时变MA系数矩阵可以用墨西哥帽小波基函数展开表示
(7)
其中,pa为时变AR系数拟合阶数,pc为时变MA系数拟合阶数。将式(7)代回TARMA模型,可得FS-TARMA模型如下
e[t]⟺x[t]=
e[t]⟺x[t]=θTφ[t]+e[t]
(8)
其中,参数矩阵θT和回归向量φ[t]具有如下形式
(9)
(10)
其中,“⊗”为Kronecker积算子,基函数向量ρ[t]具有如下形式
(11)
由式(9)可知,参数矩阵θT为常数矩阵。通过将TARMA模型参数矩阵表示为一组以墨西哥帽小波基函数的线性组合,可将时变的TARMA模型转化为时不变的FS-TARMA模型,从而把时变模型参数估计问题转化为时不变模型参数估计问题。
2.2 时变系数的两步最小二乘估计
根据参数估计原理,对式(8)中TARMA模型的残差序列均方误差(MSE)求和,得到估计的费用函数为
(12)
利用最小化MSE准则(MMSE),获得待估参数估计
(13)
式中:arg min(·)为最小化算子,即当费用函数取最小值时变量的取值。
从式(12)不难看出,由于残差序列中存在MA部分,即回归向量φ[t]中包含了残差的过去时刻值,所以估计参数θT的过程是一个非线性优化问题。为解决该问题,常常需要将非线性优化过程转化为线性求解过程,鉴于TARMA模型具有截断形式的特点,本节采用两步最小二乘法对该非线性优化问题进行线性化求解。
TARMA模型的一个基本性质是:任意阶的TARMA模型都可以用一个无限阶的TAR模型或TMA模型(也称为逆函数表达)来等价表示[7]。两步最小二乘法的基本思想是利用TARMA模型的等价性质,将TARMA模型转化为两个可以线性求解的TAR模型:第一步将TARMA模型相等价的无限阶TAR模型进行截断,求出该模型的残差序列值;第二步利用该残差序列值当做先验已知的MA部分,代入到原TARMA模型中。TARMA模型的逆函数可表达为
C-1[B,t]∘A[B,t]·x[t]=
C-1[B,t]∘C[B,t]·e[t]⟺
H-1[B,t]x[t]=e[t]
(14)
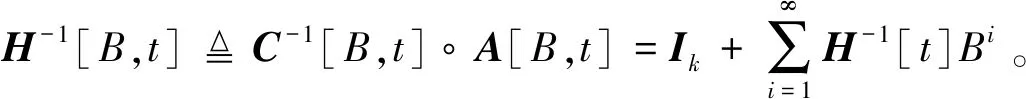
两步最小二乘的步骤可分为如下两个部分:
1) 逆函数估计
对式(14)中H-1[t]取ng阶截断,截断后的逆函数模型如式(15)所示。
x[t]=hT·φH[t]+e[t,h]⟺
(15)
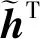
(16)
(17)
2)AR和MA系数估计
(18)
同理利用最小化MSE准则,获得待估参数估计
(19)
2.3 模型结构问题的讨论
第2.2节讨论了模型结构已知情况下的墨西哥帽小波基FS-TARMA时变模态参数估计方法,在实际情况下,模型结构往往是未知的,需要首先解决模型结构的选择问题。对于确定性结构化TARMA模型而言,模型结构的选择问题可以分为两个子问题:一是模型的阶数选择,二是模型的结构参数选择。
对于墨西哥帽小波基FS-TARMA时变模态参数估计方法的模型结构选择问题,主要包括对逆函数截断阶数ng、AR阶数na、MA阶数nc、时变AR系数拟合阶数pa和时变MA拟合系数pc的选取。
为了控制模型的过拟合程度,需要采取一些准则对拟合程度进行定量描述,常用的准则包括赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则(Bayesian Information Criterion)和残差平方和准则(Residual Sum of Squares,RSS)[27-28],本文采用RSS准则对TARMA模型的模型阶数进行选取。定义TARMA模型的残差平方和
(20)
残差平方和在一定程度上描述了TARMA模型对信号的拟合误差,因此可以控制模型的过拟合程度。基于RSS准则选取TARMA模型的模型阶数的步骤如下。
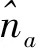

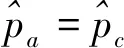
值得说明的是,较高的模型阶数可以更好地拟合信号,从而RSS准则一般相对较小;较低的模型阶数意味着较高的计算效率,更低的计算复杂度。从信号拟合的角度来看,模型阶数偏向于取大,然而在TARMA模型的模态参数辨识过程中,需要考虑实际的物理系统。当模型阶数大于实际物理阶数的时候,系统的特征根数量增多,辨识结果中会出现大量的虚假模态,虚假模态的剔除是十分困难的;当模型阶数过低,极端情况下往往会无法辨识出正确模态。因此,在模态参数辨识领域,模型阶数的选取不仅是信号拟合与计算效率之间的折中,更是物理系统先验知识和计算效率之间的折中。
3 算例验证
针对运载火箭的仅输出模态分析,本质上是对运载火箭动力学响应的分析,运载火箭的动力学响应数据一方面来源于实验/工作条件下的实测数据;另一方面来源于运载火箭物理模型的数值计算,即动力学的正问题。运载火箭的动力学响应实测数据对于研究者而言往往代价高昂,因此研究运载火箭的正问题不仅能获得系统的动力学响应,基于力学原理建立的反映系统物理特性的动力学模型对运载火箭结构设计与验证也具有重要意义。
为了验证本文所提出的墨西哥帽小波基FS-TARMA时变模态参数估计方法的有效性,本节将对运载火箭时变动力学正问题进行建模,为方法的验证提供数据基础,时变结构动力学建模的流程如图1所示。
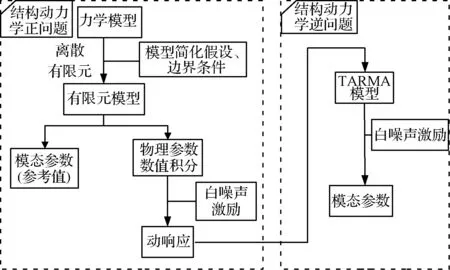
图1 运载火箭时变结构动力学建模流程图Fig.1 The work flow of time-varying dynamic modelling for launch vehicle
3.1 运载火箭时变有限元模型
根据振动理论,一个具有nd个自由度的线性振动系统,可以用一个nd维的二阶微分方程组来描述
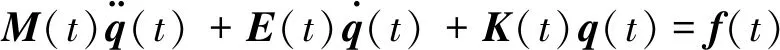
(21)

目前,商业软件目前并不具备分析时变结构动力学问题的功能。因此,针对运载火箭的结构动力学正问题,以阿里安V-versatile芯级为原型,经过调研与合理假设,将芯级的各部段进行分组编号,并建立几何曲线。在得到的每段几何曲线上进行站点的划分,站点划分的数目应当满足正确描述模型的需求:对于变截面梁,至少需要三个站点以上进行描述;对于等截面梁,则根据长度进行分配,本模型中对等截面梁单元以0.5 m的尺度进行等比例划分,共得到了96个节点,95个梁单元。梁截面定义为为薄壁圆环,芯级端头和尾段为变截面梁,将结构质量和液体质量分别分配到对应的站点上,结构质量为集中质量,液体质量则在相应的站点上添加对应耦合质量。表1给出了阿里安V号芯级的建模信息。

表1 阿里安V号芯级建模关键参数Table 1 The model structure parameters of Ariane V
考虑一种质量局部显著变化工况,如图2所示。

图2 芯一级节点质量特性变化规律Fig.2 The time-varying mass feature of the first stage nodes
采用有限带宽白噪声激励作为激励源,低通截止频率为80 Hz,作用位置为头锥顶点,即整箭几何原点,作用方向沿y轴正向。
这里引入“时间冻结”概念,即在忽略结构参数的变化率后,慢时变结构连续时间变化的模态参数近似等于“特征冻结”的结构模态参数。通过对时变系统进行“时间冻结”分析,以1000 Hz的采样率获得整箭的冻结结构集合。在冻结结构集合中,给定底部固支条件,提取阿里安V号的整箭冻结结构无阻尼横向振动频率,如图3所示。

图3 阿里安V号“冻结结构”横向模态频率Fig.3 Frozen structure modal frequency of Ariane V
使用Newmark-beta数值积分法求解运载火箭时变结构的动响应,并设置比例阻尼E(t)=a0M(t)+a1K(t),其中a0=0.1,a1=0.001。提取1,40和80号节点的动响应信号如图4所示。
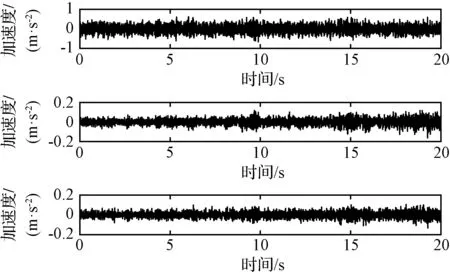
图4 加速度响应Fig.4 Acceleration responses

图5 节点1加速度响应自功率谱Fig.5 Auto-power spectrum of node 1
取节点1的加速度响应信号作时频分析,以80 Hz 进行重采样,采用短时傅里叶变换对重采样后的加速度响应信号进行分析,得到其自功率谱如图5所示。由图5可知,一阶模态的能量与其他阶相比很小,在功率谱中只能看到微弱的峰值。较弱的模态难以用辨识方法辨识出,因此,本文后续只针对运载火箭的第二、三、四阶模态的辨识效果进行讨论。为了更加全面地比较墨西哥帽小波基FS-TARMA方法辨识结构局部特征的有效性,本节将引入传统傅里叶基FS-TARMA方法作为对比。
3.2 辨识结果
1)墨西哥帽小波基FS-TARMA辨识结果
对于墨西哥帽小波基FS-TARMA方法,根据第2.3节中提到的模型结构选择方法,首先给定一组较为完备的泛函空间,取pa=pc=35,逆函数截断阶数ng=20,使得模型结构选择问题简化,只需根据RSS准则选取AR阶数na与MA阶数nc,由图5可知,在感兴趣的频带范围内,具有4阶横向频率,因此na至少需要为6,设置初始搜索区间[6,12],以节点1的振动响应信号选取模型阶数如图6所示,na=10和nc=8时RSS曲线变得平缓,因此选择其作为模型阶数的推荐值。最终确定的模型结构为pa=pc=35、ng=20、na=10和nc=8,利用节点1~96共96组振动响应数据进行分析,基于墨西哥帽小波基FS-TARMA方法的辨识结果如图7所示。
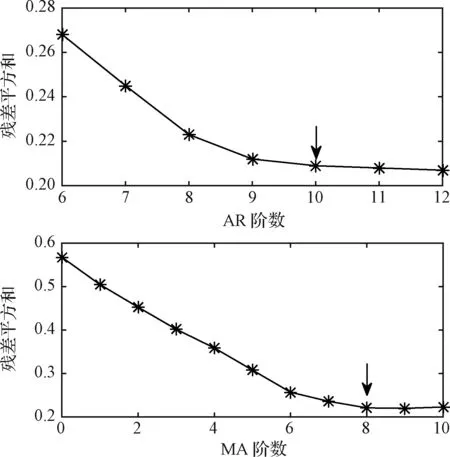
图6 墨西哥帽小波基FS-TARMA模型阶数选择Fig.6 Model selection of Mexican hat wavelet basis FS-TARMA
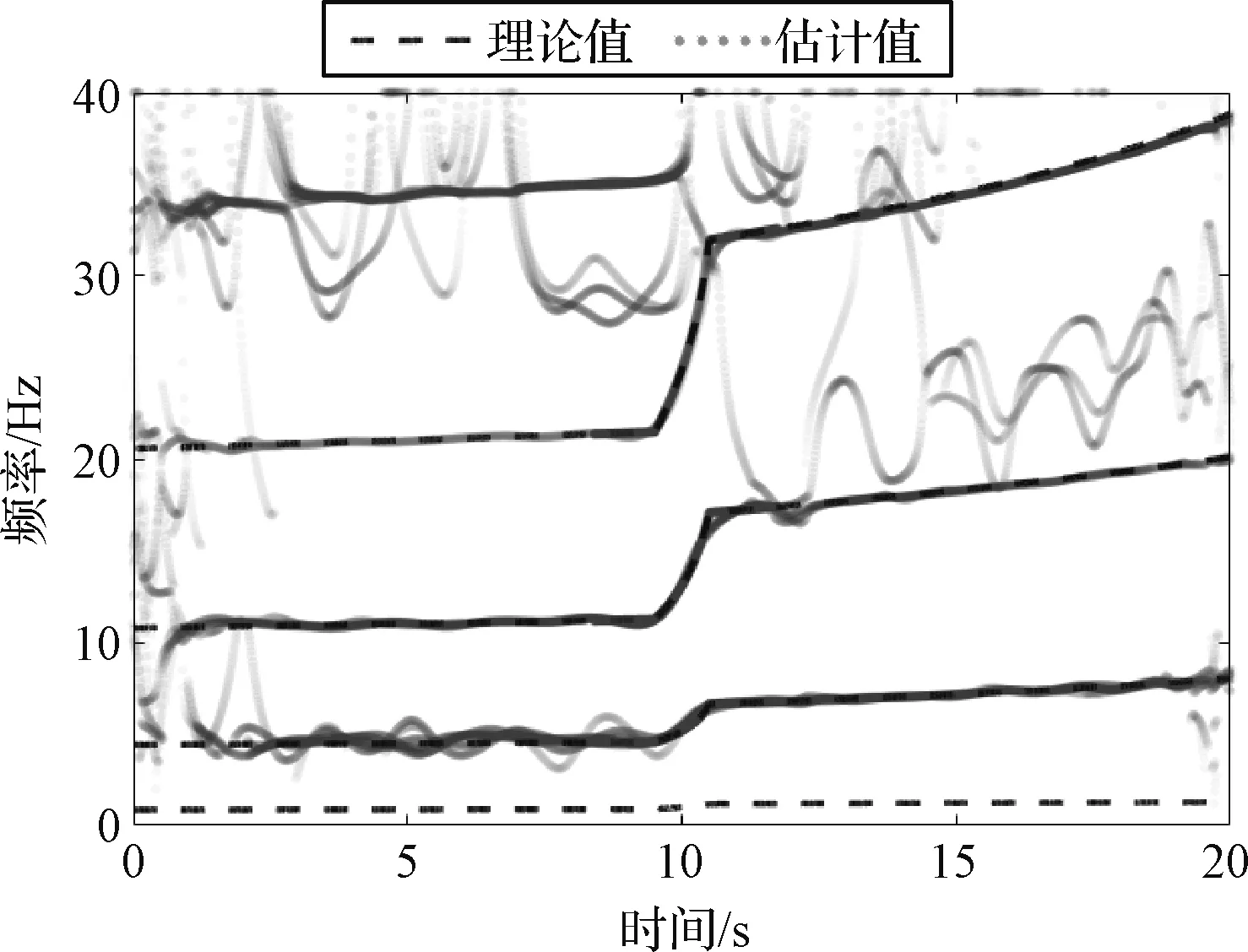
图7 墨西哥帽小波基FS-TARMA模态参数辨识结果Fig.7 Modal frequency estimation results of Mexican hat wavelet basis FS-TARMA
2)傅里叶基FS-TARMA辨识结果
对于傅里叶基FS-TARMA方法,其模型结构与墨西哥帽小波基FS-TARMA方法的模型结构类似,区别在于其拟合时变系数的泛函空间的基函数不同,本方法采用傅里叶基作为泛函空间的基底,其形式如下所示[7]:
(22)
傅里叶基FS-TARMA方法的模型结构包括截断阶数ng、AR阶数na、MA阶数nc、时变AR系数拟合阶数pa和时变MA拟合系数pc。同理,根据第2.3节中提到的模型结构选择方法,首先给定一组较为完备的泛函空间,取pa=pc=35和逆函数截断阶数ng=20,使得模型结构选择问题进一步简化,只需要根据RSS准则选取关键的AR阶数na与MA阶数nc,以节点1的振动响应信号选取模型阶数如图8所示。最终确定的模型结构为pa=pc=35、ng=20、na=10和nc=8,利用节点1~96共96组振动响应数据进行分析,基于傅里叶基FS-TARMA方法的辨识结果如图9所示。

图8 傅里叶基FS-TARMA模型阶数选择Fig.8 Model selection of Fourier basis FS-TARMA
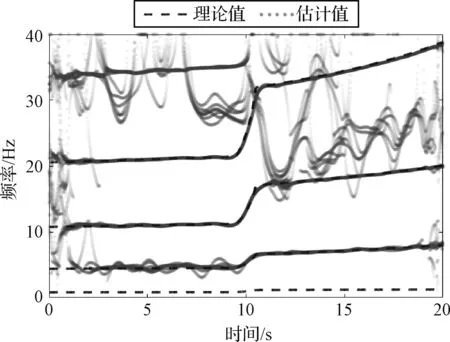
图9 傅里叶基FS-TARMA模态参数辨识结果Fig.9 Modal frequency estimation results of Fourier basis FS-TARMA
3)方法的对比分析
由图7和图9可知,两种方法均能较好地辨识出时变结构的第二、三、四阶横向固有频率。此外,与傅里叶基FS-TARMA的模态参数辨识结果相比,墨西哥帽小波基FS-TARMA的虚假极点较少,辨识结果较为“干净”。
为了定量比较不同模型的辨识精度与时变跟踪能力,定义均值绝对误差(Mean absolute error,MAE)为[29]
(23)
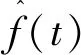
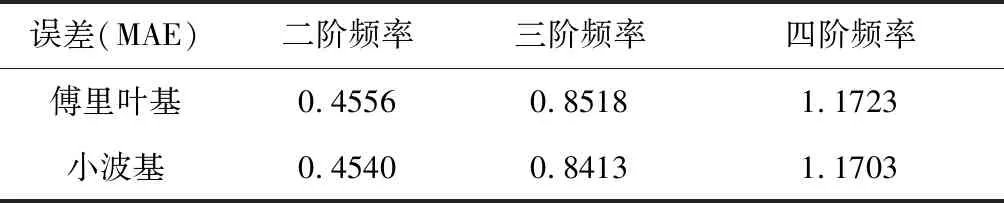
表2 模态频率估计误差Table 2 MAE values for different methods
由表2可知,本文所提的小波基FS-TARMA方法,在辨识精度上要略好于基于传统的傅里叶基FS-TARMA方法。为了能够在局部模态频率迅速变化处更好地比较两种方法的优劣,这里对辨识结果进行局部放大,如图10所示。
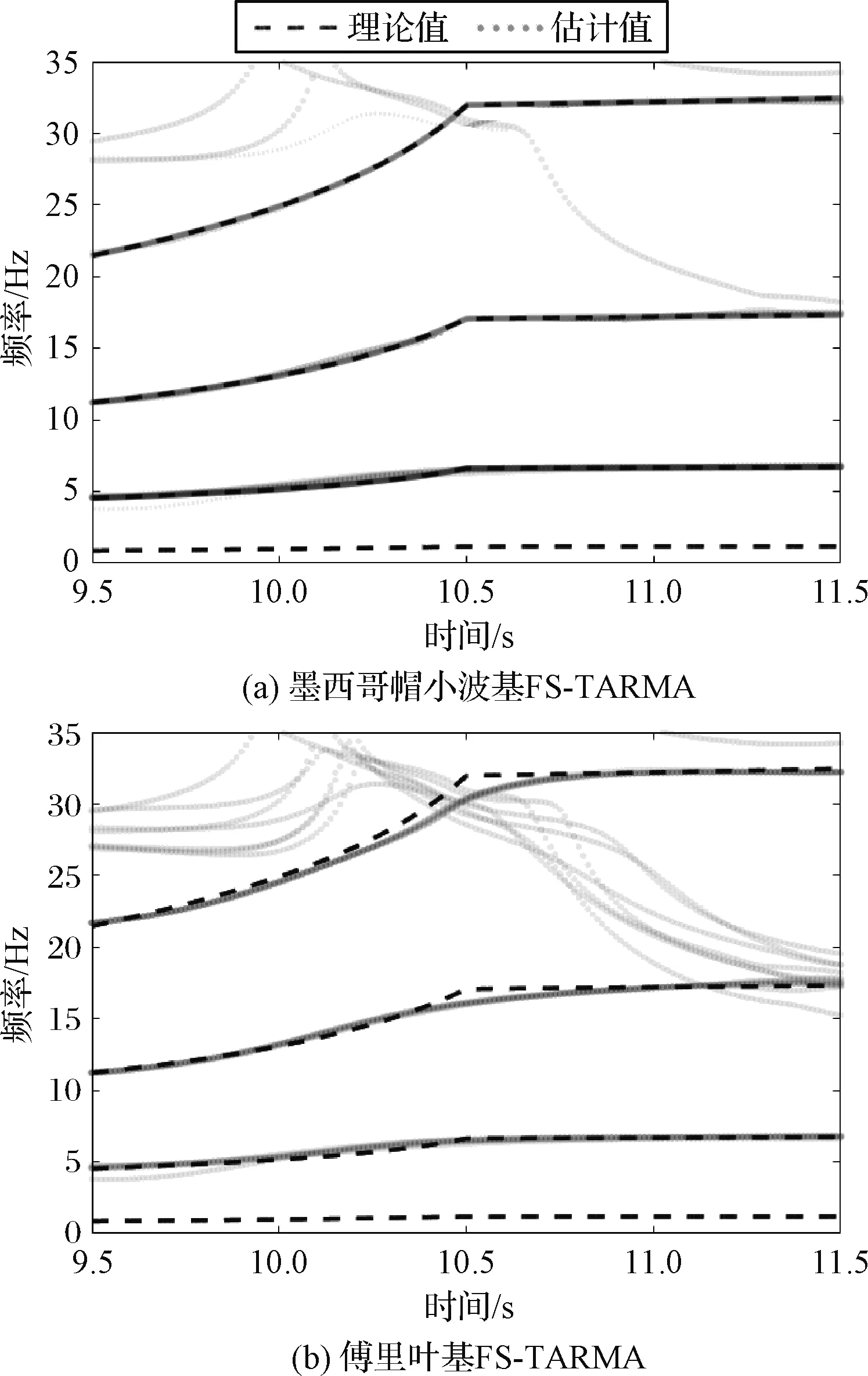
图10 模态参数辨识结果局部放大图Fig.10 The local detail of modal frequency estimation results for different methods
由图10可知,对于模态频率拐点处,墨西哥帽小波基FS-TARMA方法可以更好地拟合局部细节特征,而传统的傅里叶基FS-TARMA方法则只能平滑过渡。因此,对于具有局部细节特征的非平稳振动信号的辨识问题,与传统傅里叶基FS-TARMA相比,本文所提的小波基FS-TARMA时变结构模态参数估计方法虚假极点更少,估计精度更高,并且能够准确反映模态局部特征。
4 结 论
本文针对运载火箭时变结构模态参数辨识问题,基于TARMA模型,在时变系数的确定性演化方法上展开了研究。利用小波函数能够较好反映信号局部细节的特点,选择墨西哥帽小波函数作为TARMA模型时变系数泛函空间的基底,构建了基于墨西哥帽小波基的FS-TARMA模型。利用分步解耦思想以及TARMA模型与无限阶截断模型相等价的原理,采用两步最小二乘法对时变系数实现了解耦估计。通过建立的阿里安V号芯级运载火箭时变有限元模型,对所提辨识方法进行了验证,结果表明:针对非平稳振动响应信号,本文所提墨西哥帽小波基FS-TARMA方法可以准确地对时变系统的模态频率进行估计,与传统傅里叶基FS-TARMA相比,具有更好的辨识精度,并能够较好地反映出模态局部细节特征。

