地基光学图像中本体-帆板结构航天器姿态估计方法
杨 成, 李 勰, 李志辉, 孙 军
(1. 北京航天飞行控制中心,北京 100094;2. 航天飞行动力学技术重点实验室,北京 100094; 3.中国空气动力研究与发展中心,绵阳 621000)
0 引 言
三维姿态信息是反映空间目标运动状态的重要参数,对空间态势感知、目标运动分析、航天器运行控制和故障诊断具有重要意义。空间目标的观测主要采用地基雷达观测和光学观测两种方式[1-3]。雷达观测向目标发射电磁波并接收返回信号,属于主动探测,其探测能力与作用距离的四次方成反比,主要作用于近地轨道空间。光学观测属于被动观测,探测能力与距离的平方成反比,具有更好的跟踪能力。随着光学成像设备性能的发展,地基光学图像在空间目标姿态估计的应用越来越多[4-5]。
从图像信息中提取空间目标姿态主要有两类方法。一类是模板匹配方法,根据空间目标的几何外形、表面材质和空间构造等三维模型信息,预先仿真不同姿态下的观测图像,建立目标观测图像库,然后将实际观测图像进行图像匹配,根据匹配相似度确定目标的姿态。这类方法需要提前构建匹配图像库,在姿态估计过程中进行大量的匹配处理,具有较高的计算复杂度,实际应用中效率较低,且需要定义合适的图像匹配相似度,对姿态估计的结果有较大影响[6-8]。另一类是直接根据三维空间到二维图像的投影关系进行解算,一般是通过提取图像特征,根据计算机视觉成像原理,建立空间三维信息到二维图像的几何投影模型,根据特征在二维图像的像素坐标反算出三维空间坐标,从而确定目标的三维姿态。这类方法避免了建立图像库和匹配搜索处理,但空间目标的特征可能被遮挡,无法实现任意姿态的估计[9-11]。
本文提出一种本体-帆板结构航天器的姿态估计方法。针对该类航天器几何外形结构特点,定义航天器本体主轴和帆板转动轴两轴结构作为图像特征,提出了地基光学图像边缘模糊条件下的特征提取方法,根据三维空间到二维图像投影方程,建立了航天器姿态解算方法,实现了单站序列图像姿态和角速度估计。
1 地基光学图像特征提取
1.1 本体-帆板结构航天器外形特点
航天器包括本体、帆板及天线、敏感器等结构和部件。本体一般为方形或者圆柱形,是航天器的主体,同时为其它仪器设备和有效载荷提供安装框架。帆板具有较大的尺寸,一般为左右两部分分别连接在本体两侧,为航天器提供能源[12]。天线、敏感器、发动机等载荷安装在本体表面,其尺寸相对本体和帆板很小,在进行表面力建模和光学图像分析等处理时可忽略不计。因此,这类航天器在进行几何外形建模时可简化为本体和帆板两部分组成,称为本体-帆板结构(Box-Wing)航天器。
图1 航天器本体-帆板结构示意图Fig.1 Schematic diagram of Box-Wing spacecraft
1.2 图像特征定义
地基光学雷达对空间航天器进行观测,根据视觉原理产生图像,其成像几何原理和地面景物成像一致。由于航天器距离地面光学设备的成像距离非常大,成像视场角很小,航天器于空间高速运行,因此图像的信噪比非常低,椒盐噪声影响严重。同时,成像过程跨越大气层,导致成像信息的边缘非常模糊。这些都给图像特征的准确提取带来了影响。如图2所示,在光学图像中,可根据航天器形状先验知识,辨认出帆板、本体结构,而其它载荷部件的细节丢失。
针对航天器本体-帆板结构特点,定义光学图像中航天器左、右帆板和本体结构的端点作为图像特征,获取三点的像素坐标恢复航天器三维姿态。如图3所示,P(+X)为本体前端面中心点,P(-Y)为左帆板外测边缘中心点,P(+Y)为右帆板外测边缘中心点,P(-Y)和P(+Y)连线中点记为P0。

图3 图像特征点定义Fig.3 Definition of feature points
1.3 图像特征提取
利用数字图像处理方法,从光学图像提取特征点的像素坐标[13],步骤如下所述。
1)图像增强。首先对图像进行中值滤波,消除图像中椒盐噪声影响;然后进行膨胀,恢复图像中的连通性。
2)边缘检测。对图像进行Harris边缘检测,对边缘检测结果使用连通性检测得到最长的边缘曲线作为航天器的边缘。待提取的特征点位于检测出的边缘曲线上。

图5 边缘检测结果Fig.5 Results of edge detection
3)特征点确定。根据帆板形状拟合出帆板边缘位置,获得帆板的中心点和帆板转轴方向,确定P(-Y)和P(+Y)两特征点的位置;然后查找剩下边缘点的中点,即为P(+X)特征点的位置。
当图像中航天器帆板、主体结构完整清晰时,可用上述图像处理方法自动获得特征点的像素坐标;若成像质量差或者处于遮挡严重的角度图像中航天器结构不完整,采用人工标注的方法提取特征点。
2 航天器姿态解算
2.1 投影方程解算
在地基光学设备对空间目标跟踪成像过程中,按照成像模型,定义光学设备坐标系如图6所示,坐标原点为光心,Y轴指向地心,Z轴沿主光轴指向空间目标方向,X轴与Y轴、Z轴构成右手坐标系。产生的空间目标光学图像位于X-Y平面,图像坐标系像素坐标X轴为水平向右,Y轴为垂直向下。
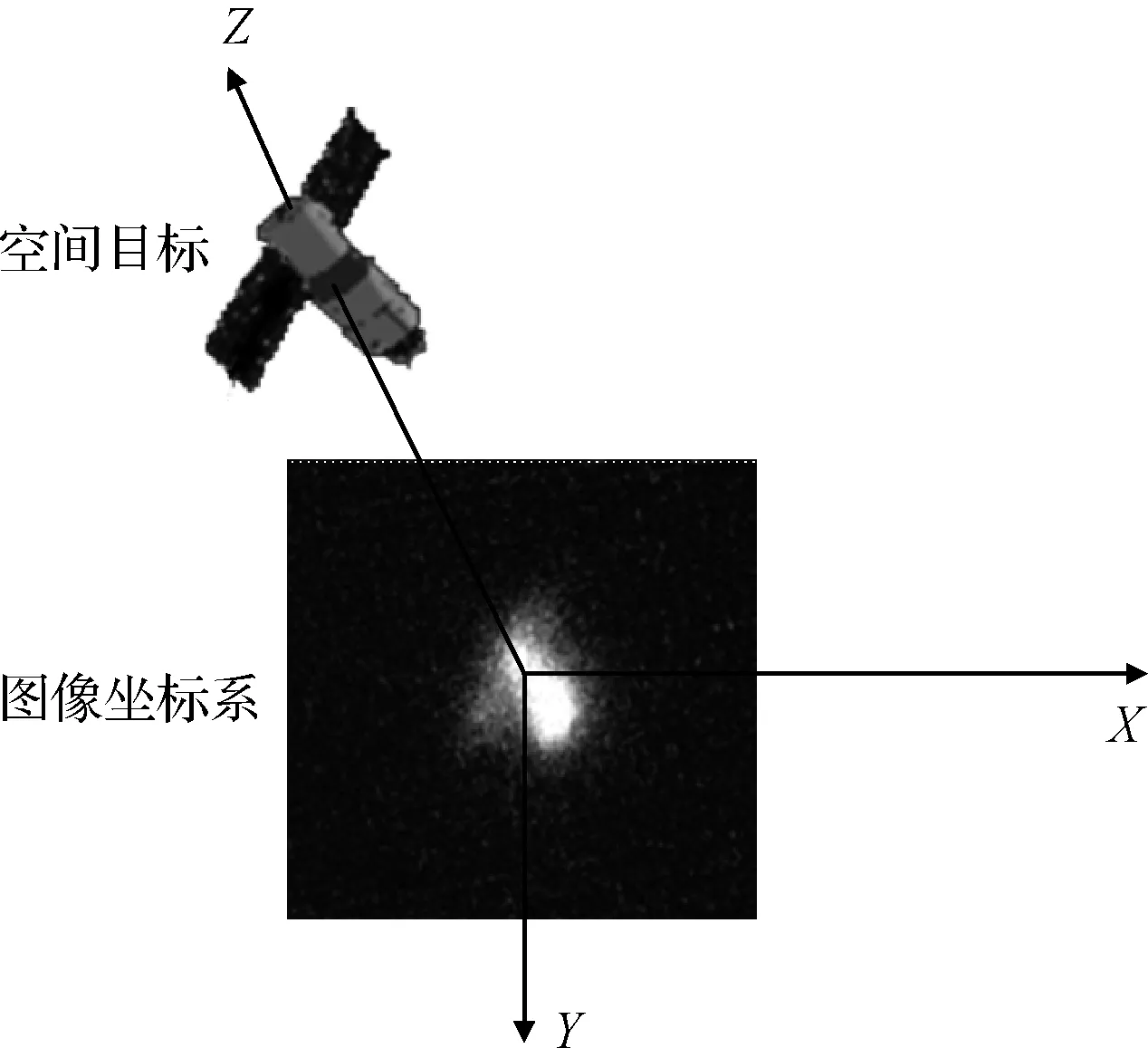
图6 光学设备坐标系定义Fig.6 Coordinate of optical telescope
对于本体-帆板结构航天器,根据其结构特点,本体系定义为:本体主轴和帆板转动轴交点为原点,本体主轴向前进方向为X轴,Y轴为转动轴,Z轴与X轴、Y轴构成右手坐标系。
记地面光学图像提取到的特征点像素坐标分别为:
(1)
(2)
(3)
帆板中点P0坐标为:
P0=(P(+Y)+P(-Y))/2
(4)
光学图像像素分辨率k表示一个像素对应空间中的物理长度,帆板中点至本体前端点在光学图像的二维投影坐标为P(+X)-P0,则其在光学设备坐标系下X-Y坐标为k(P(+X)-P0)。由于航天器本体坐标系的X轴定义为帆板中点至本体前端点方向,则航天器本体坐标系的X轴在光学设备坐标系下坐标可表示为:
(5)
式中:l1为根据航天器的几何尺寸中,帆板中点P0至本体前端点P(+X)的长度;由于投影平面为X-Y平面,Z轴方向的坐标不能确定,用未知量z1表示。
同理,航天器本体坐标系的Y轴在光学设备坐标系下坐标可表示为:
(6)
式中:l2为根据航天器的几何尺寸中,帆板中点P0至右帆板外测边缘中心点P(+Y)的长度;由于投影平面为X-Y平面,Z轴方向的坐标也不能确定,用未知量z2表示。
本方法没有在光学图像中提取航天器本体坐标系Z轴的特征,其在光学设备坐标系下坐标用Zc来表示,则航天器本体坐标系到光学设备坐标系的旋转矩阵为:
(7)
由Xc,Yc为正交单位向量,可得如下方程:
(8)
(9)
(10)
式中:k,z1,z2为未知量,满足k>0,|z1|≤1,|z2|≤1。
根据式(8),z1可变换为k的表达式;根据式(9),z2也可变换为k的表达式。代入式(10)中,得到关于k的方程,可求得k的可能解。根据约束条件,最终可确定k,z1,z2的两组解,进而求得Xc和Yc,利用Zc=Yc×Xc,即可得到航天器本体坐标系到光学设备坐标系的旋转矩阵RI=[Xc,Yc,Zc]3×3。
上述方法通过二维图像信息,确定了三维空间中航天器对应的两种可能姿态,这两种姿态关于相机成像平面成镜像关系,通过单张图像不能确定唯一姿态。实际应用中,地面光学设备会间隔一定时间持续对航天器进行观测,通过序列图像恢复姿态之间的关联性,对两种可能结果进行合理性判断,确定航天器唯一的姿态结果。
2.2 姿态坐标系转换
1)光学设备坐标系到测站坐标系的转换
定义测站坐标系原点为光学设备跟踪天线的旋转中心,X-Z平面为经过坐标原点的地球切平面,X轴位于该切平面指向东,Z轴指向北,Y轴与X轴、Z轴形成右手坐标系。在对空间目标进行观测过程中,需要通过转动观测设备的方向来瞄准空间目标,产生方位角A和仰角E,如图7所示。

图7 测站坐标系定义Fig.7 Coordinate of observer station
方位角A旋转矩阵为:
(11)
仰角E旋转矩阵为:
(12)
图像坐标系到测站坐标系的旋转矩阵为:
RA×RE
(13)
2)测站坐标系到地球惯性系的转换
记测站在地球惯性系的位置坐标为P,可计算出测站坐标系Y轴向量,Y轴与数值单位向量[0,0,1]的叉乘,可得到测站坐标系X轴向量,然后Y轴与X轴叉乘得到Z轴向量。于是得到测站坐标系到地球惯性系的旋转矩阵RC。

图8 测站坐标系和地球惯性系示意图Fig.8 Relationship of observer station and J2000 coordinates
3)地球惯性系到轨道坐标系的转换
根据航天器在地球惯性系的位置和速度矢量,可算出航天器轨道坐标系与地球惯性系的旋转矩阵RO。
4)欧拉角计算
可算出航天器本体系在地球惯性系的旋转矩阵为[14]:
MJ2000=RC×RA×RE×RI
(14)
航天器本体系在轨道系的旋转矩阵为:
MOrbit=RO×RC×RA×RE×RI
(15)
采取“偏航-滚动-俯仰”的顺序来进行姿态旋转,旋转矩阵M3-1-2和偏航(ψ)-滚动(φ)-俯仰(θ)欧拉角之间的转换关系为:
(16)
由式(16),根据航天器旋转矩阵可反推出航天器偏航-滚动-俯仰角度。
3 试 验
3.1 实验设置
利用我国地面光学设备获取的空间在轨航天器图像对本文方法进行验证。航天器为舱体-帆板结构,如图1所示,舱体为圆柱状,前端面为锥形,帆板连接于舱体后半部分。本体坐标系X轴沿舱体指向前锥面,Y轴指向右帆板,Z轴与X轴、Y轴形成右手坐标系。航天器帆板展开后长度约30 m,轨道高度约400 km,处于慢速自旋状态。
地面观测站位于我国西南地区,如图9所示,观测弧段内,航天器沿图中轨迹左上点往右下方向飞行,光学设备间隔5 s获得航天器光学图像。本次观测过程中,成像时间在凌晨5点左右,成像距离约600 km,成像方位角约-10°~70°,俯仰角约20°,共获得14张图像,用于本文姿态估计方法实验。

图9 航天器经过观测站上空的路线Fig.9 The routine of spacecraft over ground station
3.2 实验步骤
对每张图像处理过程如下所述。
1)使用第1.3节的方法或者人工方式提取图像中航天器三个特征点的像素坐标,代入第2.1节方程(8)~(10)中进行投影方程解算,获得航天器本体坐标系到光学设备坐标系的旋转矩阵RI。
2)根据图像对应的观测设备方位角A和仰角E,计算光学设备坐标系到测站坐标系的旋转矩阵RA×RE。
3)根据航天器轨道根数和观测站的经纬度,获得该幅图像观测时刻航天器在地球惯性系的位置和速度,以及观测站在地球惯性系的位置。按照第2.2节中的方法,得到航天器在地球惯性系和轨道坐标系的旋转矩阵,并计算相应的姿态欧拉角。
3.3 姿态估计结果
为便于分析,以“偏航-滚动-俯仰”顺序的欧拉角来表示姿态。每幅图像都得到两个可能的解,对应两种不同的航天器姿态。对14幅序列图像进行处理,得到了两组可能姿态。
第一组姿态结果如表1所示,单位为度(°)。

表1 第一组可能的姿态结果Table 1 Estimation of the first probable attitude
图10和图11为第一组姿态角度和拟合情况,实线为根据图像估计的角度数据,虚线为根据序列图像估计结果进行一次拟合的直线。
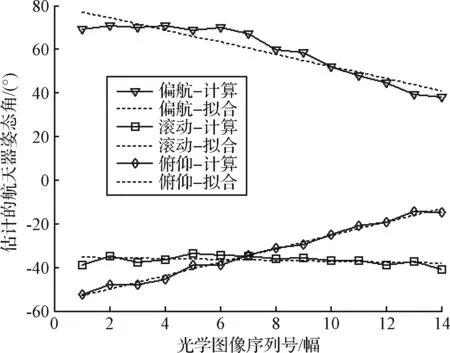
图11 航天器轨道系姿态结果(第一组)Fig.11 Estimation of attitude in orbit coordination (The first group)
第二组姿态结果如表2所示。
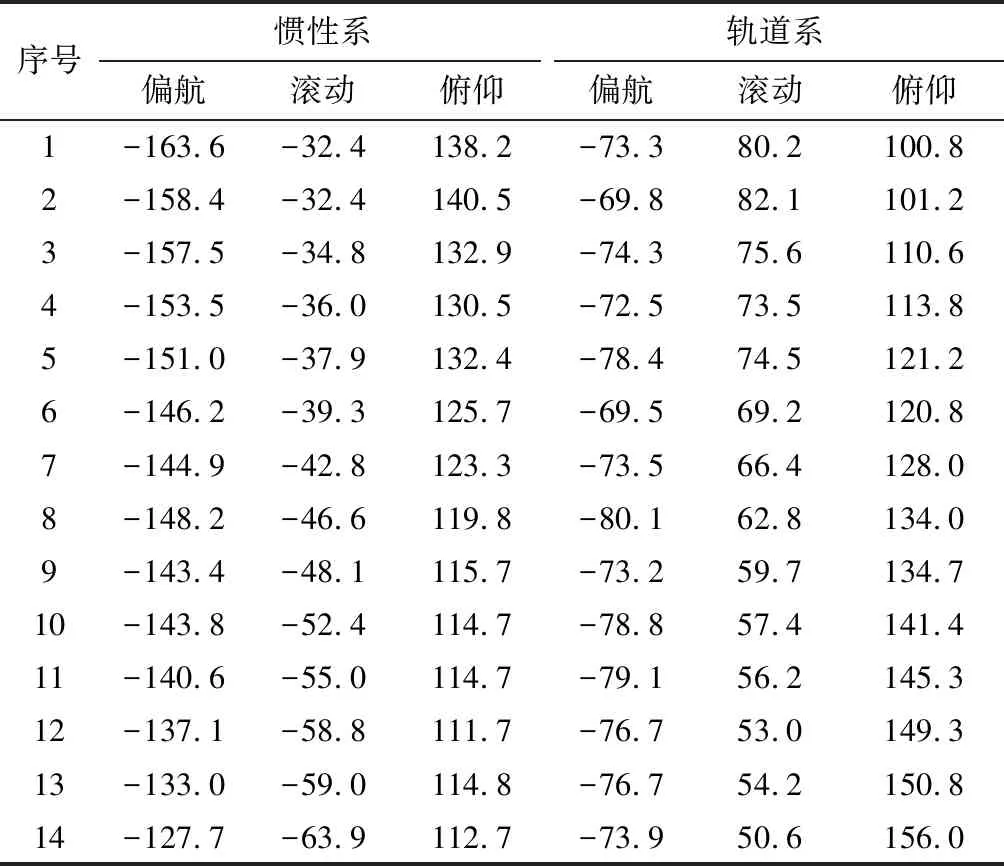
表2 第二组可能的姿态结果Table 2 Estimation of the second probable attitude
图12和图13为第二组姿态角度和拟合情况,实线为根据图像估计的角度数据,虚线为根据序列图像估计结果进行一次拟合的直线。
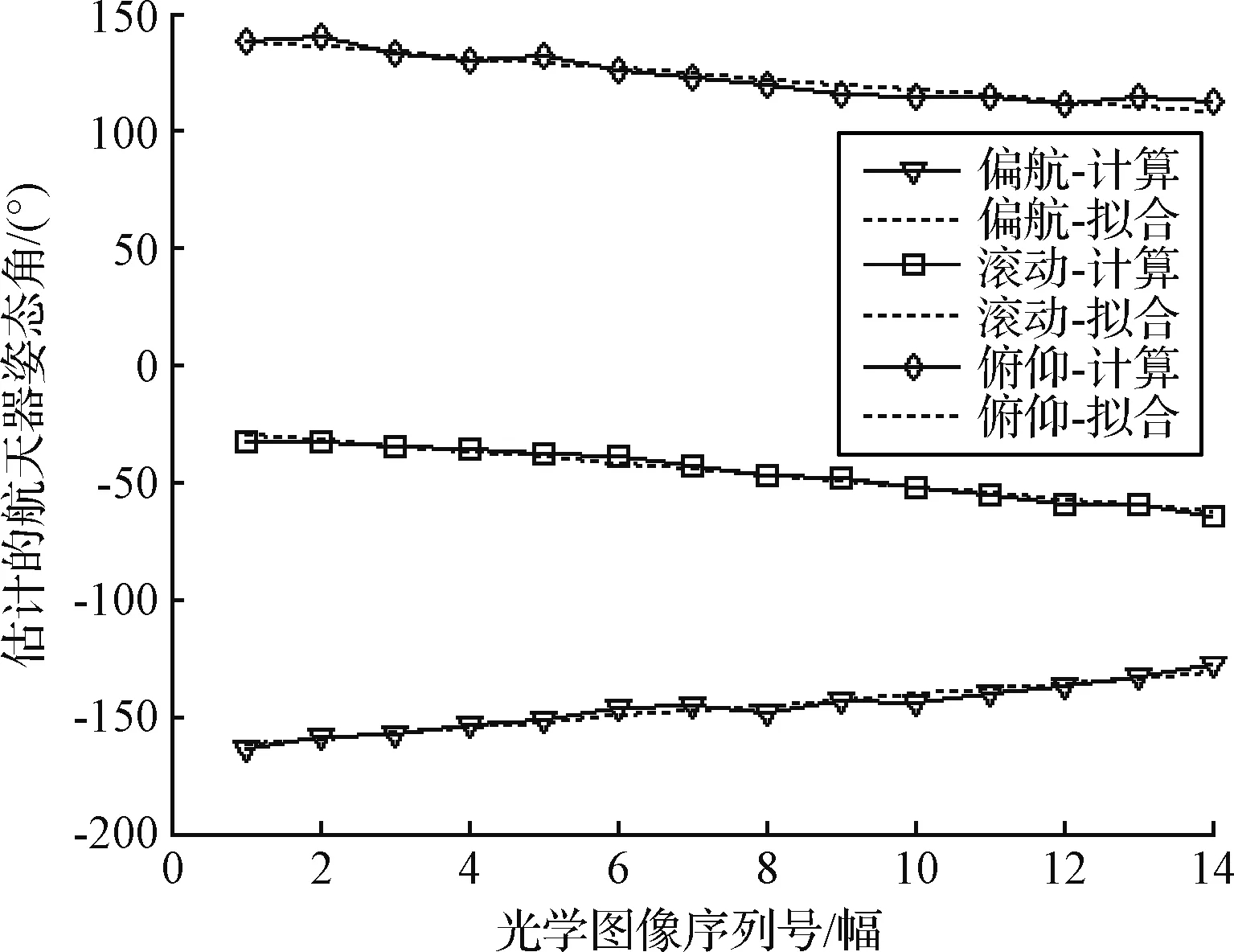
图12 航天器地球惯性系姿态结果(第二组)Fig.12 Estimation of attitude in J2000 coordination (The second group)
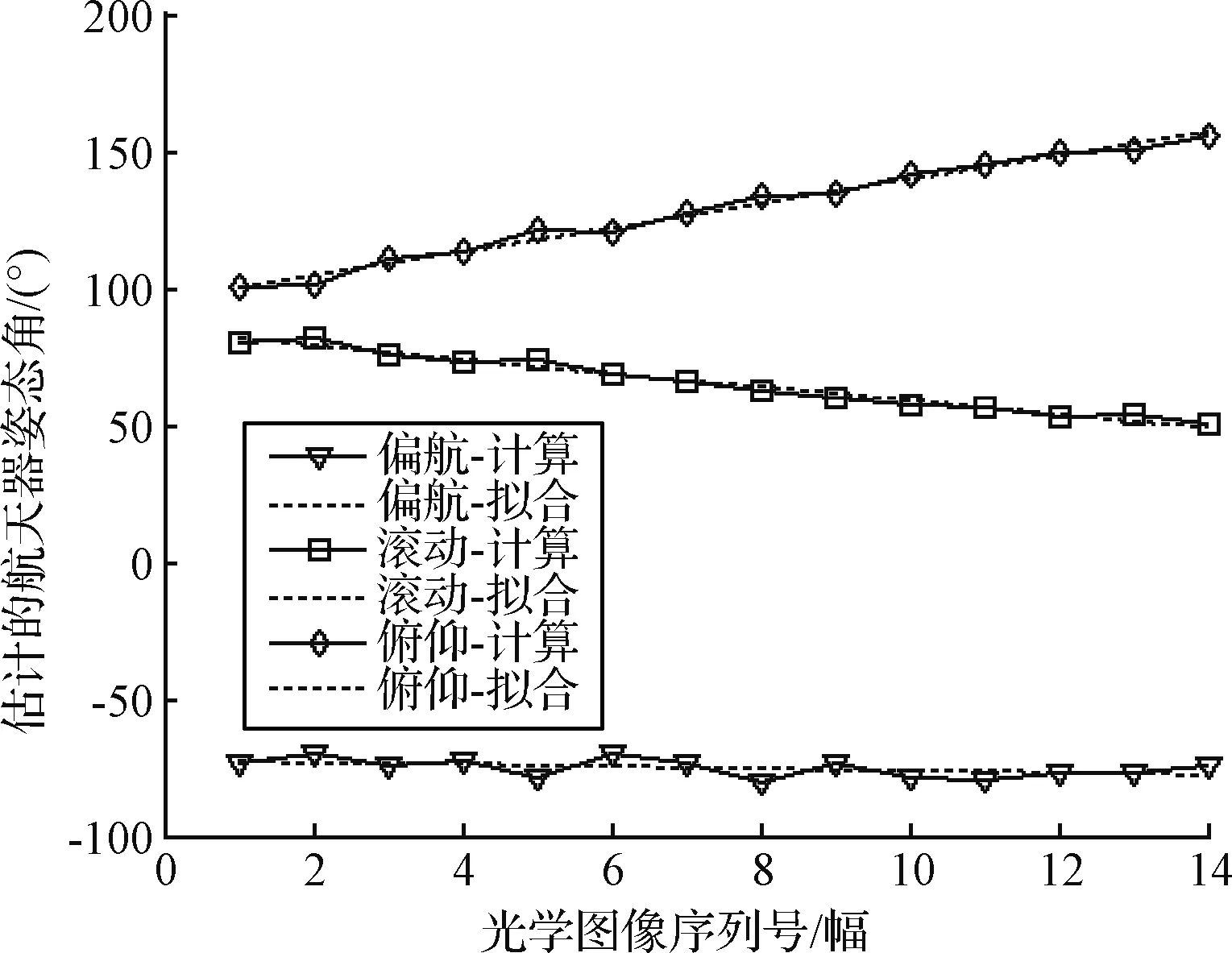
图13 航天器轨道系姿态结果(第二组)Fig.13 Estimation of attitude in orbit coordination (The second group)
本次实验14幅图像数据间隔5 s,航天器在此期间处于无控飞行状态,其姿态变化为匀速旋转。通过对姿态角度进行线性拟合,得出偏航、滚动、俯仰角度的旋转角速度。利用拟合的一次曲线作为理论姿态角度,可得出本文方法估计结果的均方误差如下:
(17)
式(17)中θ′i为本方法估计的姿态角度,θ′i为一次曲线拟合姿态角度,对应均方差反应了本文方法估计姿态角度的一致性。两组可能姿态的角速度和结果方差如表3所示。
从图10~13和表3可以看出,第二组姿态结果均方差更小,对航天器慢速旋转状态拟合较好,确定第二组姿态为估计结果。图14为第二组结果对应的航天器姿态情况,在序列图像成像时刻航天器的位置,绘制航天器本体系坐标轴,可直观地看出航天器姿态变化情况。

表3 两组姿态估计结果Table 3 Two probable results of estimated attitude

图14 估计出的航天器姿态Fig.14 Visualization of the estimated attitude
4 结 论
本文提出了一种从光学图像估计航天器姿态的方法。针对舱体-帆板结构航天器的几何外形特点,定义了三个易于提取的特征点,并设计了基于图像边缘检测的自动特征提取算法;建立了特征点二三维投影方程,实现了对三维姿态的求解。本方法无需建立大量的模型匹配库,避免了复杂的匹配搜索过程,可直接根据特征点获得姿态结果。对在轨航天器进行了光学图像姿态估计实验,姿态角进行线性拟合后的平均估计误差在3°以内,验证了本方法的有效性。

