CE- 4中继卫星使命轨道维持与动量轮卸载联合控制方法

马传令, 刘 勇, 陈 明, 刘 磊, 梁伟光

(1. 北京航天飞行控制中心，北京 100094；2. 航天飞行动力学重点实验室，北京 100094)

0 引 言

动量轮是现代卫星姿态控制系统的代表性执行机构。随着卫星功能不断增加，大功耗、大口径抛物面天线广泛应用，由于其相对星体安装不对称的特点，使得星体所受外干扰力矩进一步增大，给卫星设计和在轨管理过程中动量轮卸载控制提出了新的要求[1]。

嫦娥四号中继卫星的使命轨道为地月L2平动点Halo轨道。一方面，由于卫星结构不对称性，使得轮控调姿期间受太阳光压的影响，存在角动量积累现象，动量轮饱和时的喷气卸载会对使命轨道产生非预期扰动；另一方面，Halo轨道在真实力学环境下具有不稳定性，长期运行时需定期维持控制以保持轨道构型[2-3]。

近年来，国内外对动量轮卸载的研究主要集中在地球低、高轨卫星等具有特殊结构或执行新的任务的航天器上，文献[4-8]针对偏置动量卫星的角动量管理特点，研究了静止轨道卫星东西位置保持优化策略。针对平动点周期轨道卫星角动量管理的公开研究文献很少，戴居峰等[9]对“嫦娥二号”卫星进入环绕日地L2平动点Lissajous轨道的卫星喷气卸载所产生的影响进行了研究，提出了一种利用光压力矩辅助卫星太阳电池翼角度调整进行角动量管理的方法；目前尚未见动量轮卸载在平动点周期轨道卫星长期运行轨道维持中的公开应用研究。

针对Halo轨道构型保持轨控策略设计，提出了一种使命轨道维持与动量轮卸载联合控制方法。首先，介绍了嫦娥四号中继卫星使命轨道维持的常规轨控策略；然后，基于卫星工程实测数据，分析了其角动量累积规律，给出了动量轮卸载前、后角动量变化量与喷气卸载等效速度增量的经验公式，并定性分析了喷气卸载对轨道构型的影响；在此基础上，提出通过偏置轨道维持控制目标抵消控后动量轮卸载扰动影响的控制策略，达到延长轨道维持控制周期和节省推进剂的目的，同时给出了控制目标偏置量的求解方法；最后，采用工程应用结果验证方法有效性。

1 Halo轨道及其维持控制策略

1.1 圆型限制性三体问题和Halo轨道

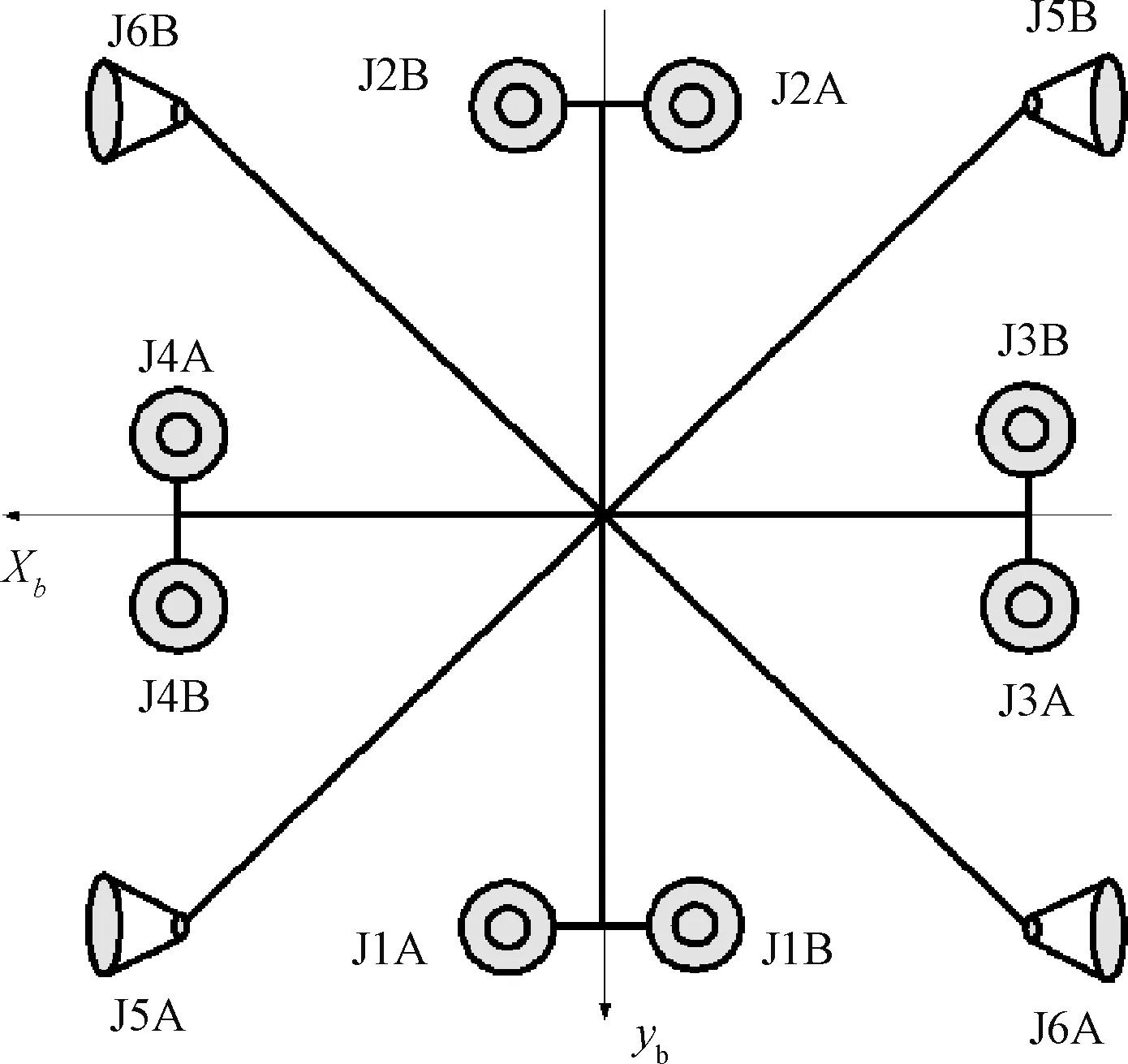
根据限制性三体假设，第三体质量为m，两个大天体质量分别为m1和m2，满足m≪m2

图1 圆形限制性三体问题平动点示意图Fig.1 Illustration of libration points of circular restricted three-body problem

描述卫星在平动点附近运动时涉及旋转坐标系。以地月系三体系统为例，地月L2点旋转坐标系定义如下：原点O在地月L2点，x轴沿地球质心指向月球质心，y轴平行于月球沿白道面运动切线方向，z轴和x轴、y轴构成右手坐标系(如图2所示)。地月L2点附近存在Lissajous轨道和Halo轨道。Lissajous轨道在地月旋转平面内和平面垂直方向的振动频率不同， Halo轨道在平面和垂直方向的振动频率相等，Halo轨道是Lissajous轨道的特例。目前工程应用中主要是这两种轨道。

嫦娥四号中继卫星承担月球背面探测器与地球之间的中继通信任务，综合考虑到月掩、星器可见性等几何条件影响，其使命轨道类型采用地月L2点Halo轨道(如图3所示)，在地月L2点旋转坐标系中其x方向振幅约1.2万km，y方向振幅约3.6万km，z方向振幅约1.3万km，光照时间比例接近100%，预计工作三年[10]。

图2 地月L2点旋转坐标系示意图Fig.2 Illustration of Earth-Moon L2 rotary coordinate system

图3 地月L2旋转坐标系Halo轨道形状示意图Fig.3 Illustration of Halo orbits in Earth-Moon L2 rotary coordinate system

1.2 Halo轨道动力学方程及求解方法

基于圆型限制性三体问题模型，Halo轨道在地月L2旋转坐标系中的动力学方程如下[11]：

(1)

(2)

而在真实力学环境下，Halo轨道及转移轨道的精确求解除需考虑太阳、地球、月球等星体的非圆型、非限制性、非三体引力影响因素外，太阳光压也是主要影响，难以找到解析解，主要采用数值积分对轨道进行精确计算[12]。轨道积分时，通常将卫星轨道参数由地心J2000坐标系转换至地月L2旋转坐标系中，判断卫星是否满足L2点的运行状态。

地心J2000坐标系Oi-xiyizi到地月L2点旋转坐标系的坐标转换计算步骤如下：

1)计算地心J2000坐标系Oi-xiyizi到公共质心旋转坐标系Oc-pqr(如图1所示)的旋转矩阵Hri和旋转角速度ωr；

(3)

式中:Re和Ve分别表示地心在地心J2000坐标系的位置和速度矢量，Rm和Vm分别表示月心在地心J2000坐标系的位置和速度矢量，R和V分别表示该坐标系月心相对地心的位置和速度矢量。

2)计算地月距变化率υ

(4)

3)计算公共质心Oc在地心J2000坐标系的位置速度矢量Rco和Vco

(5)

式中:μ表示归一化条件下地球到公共质心Oc的距离。

4)将卫星地心J2000坐标系位置速度矢量Ri和Vi转换到公共质心旋转坐标系

(6)

式中:Rc和Vc分别表示卫星在公共质心旋转坐标系的位置速度矢量。

5)将卫星位置速度Ri和Vi从J2000坐标系转换到地月L2点旋转坐标系

(7)

式中:ξl2表示地月L2点到公共质心Oc的归一化距离。

1.3 中继卫星使命轨道维持的常规轨控策略

Halo轨道族在旋转坐标系中是一个曲面，即不是在任意点都能形成Halo轨道。在给定初始点的情况下，如果该点不在Halo轨道上，则只能形成Lissajous轨道或拟Halo轨道[13]。由于地月L2点为不稳定平动点，在高精度动力学模型下不存在理想Halo轨道，中继卫星在飞行过程中受到多种摄动和误差因素的影响，需要定期进行轨道控制才能保证中继卫星在L2点附近的长期稳定运行。考虑到推进剂约束，在保证Halo轨道形状的同时尽量减小轨控所需的速度增量。中继卫星轨道维持选择拟Halo轨道的控制方式[14-15]，采用逐级微分改正方法求解控制时刻速度三方向分量，控制目标为从轨控关机点起算的第三次穿过地月L2点旋转坐标系xoz面时的x方向速度为零。轨控时机确定步骤如下：1)控制间隔需大于测定轨所需的最小时段;2)根据测控弧段选择预选轨控点，依次计算每天预选轨控点的速度增量，若速度增量大于发动机允许的开机门限，则执行本次维持控制。

2 动量轮卸载及其对使命轨道构型影响

2.1 动量轮卸载原理

太阳光压是嫦娥四号中继卫星长期在轨稳定飞行的主要干扰源之一，太阳光压相对应的压心和卫星质心不重合时，会产生太阳光压力矩，这是干扰中继卫星姿态稳定性的最主要干扰力矩。嫦娥四号中继卫星采用由偏置动量轮组成的整星零动量方案，即在各轴安装偏置动量轮，在合成动量反方向设置对称动量轮，如图4所示。动量轮转速变化可吸收外干扰力矩，实现卫星姿态稳定。

图4 星体坐标系(左)及动量轮布局(右)Fig.4 Illustration of centroid coordinate system (left) and momentum wheels layout of relay satellite (right)

当卫星受到干扰时，受扰动的卫星由于动量轮的控制作用，把多余的角动量存储于动量轮，动量轮转速获得增量Ωt-Ω0，保证了卫星定向性；当有持续干扰力矩作用于星体时，动量轮的转速随时间单调变化。当转速偏离标称转速过大或过小时,会进入饱和状态,动量轮将无力存储星体多余的动量矩,从而使卫星失控,这就是动量轮要定期卸载的原因。嫦娥四号中继卫星动量轮卸载时，使用姿控发动机喷气控制方式产生力矩以抵消干扰力矩，使动量轮转速重新回到标称转速附近，因此会对轨道产生扰动。

2.2 姿控发动机喷气卸载对轨道影响的定性分析

嫦娥四号中继卫星姿控发动机布局如图5所示，J5A/J5B和J6A/J6B为力耦姿控发动机，用于绕zb轴偏航姿态调整，J3A/J3B和J4A/J4B为非力耦姿控发动机，用于绕yb轴俯仰姿态调整，J1A/J1B和J2A/J2B为非力耦姿控发动机，用于绕xb轴滚动姿态调整。

中继卫星zb轴角动量卸载时，姿控发动机(力耦)喷气不会产生+zb方向推力，xb和yb轴角动量卸载时，姿控发动机(非力耦)喷气会产生+zb方向推力。

由于中继天线指向轴(星体+zb轴)始终对准月球，因此，若已知卸载时刻，即可得月球和卫星在地心J2000坐标系的位置，进而可得卸载时星体+zb轴在地心J2000坐标系下的单位指向矢量ni，即喷气卸载在惯性空间的推力方向，由式(3)可得卸载喷气在地月L2点旋转坐标系的推力方向n=Hri·ni，如图6所示。

图5 卫星姿控发动机布局Fig.5 Illustration of satellite attitude control engine layout

图6 喷气卸载推力方向Fig.6 Thrust directions of momentum wheel upload

2.3 卫星角动量累积规律及卸载时刻预测

地月通信中继期间，星体+zb轴指向为月球，单位矢量为TZI；星体+yb轴指向为+zb轴矢量叉乘太阳矢量，单位矢量为TYI，SI为太阳矢量；星体+xb轴符合右手定则。因此，卫星对月定向时，能确保星体+yb轴与太阳矢量垂直；星体+xb轴与+zb轴与太阳矢量夹角为0°～180°，太阳始终位于星体坐标系的xbobzb平面内，且始终在+xb轴一侧，如图8所示。

图7 地月共线平动点绕飞轨道扰动影响示意图Fig.7 Illustration of disturbance effects on orbits around Earth-Moon collinear libration points

图8 太阳光对中继通信天线照射的空间模型Fig.8 Spatial model of sunlight irradiation on satellite communication antenna

定义β为太阳在xbobzb平面内与星体+zb轴的夹角，由于中继卫星支持月球背面着陆探测的特点，太阳在星体坐标系中方向随朔望月呈周期性变化。单个朔望月内太阳位置在xbobzb平面内的β角变化如图9所示。

图9 一个月内太阳在星体坐标系β角变化Fig.9 Beta angle variation in a lunar month

由于太阳辐射压力力矩与卫星形状、质量分布、表面材料光学特性、部件之间的遮挡等多种因素有关，通过仿真模型准确模拟太阳光压力矩与角动量累积的关系，难度较大，且精度较低。下文以某个朔望月卫星工程实测角动量数据为例，对角动量累积规律进行分析，如图10所示。

图10 预处理后的一个朔望月周期内相对角动量Fig.10 Curves of momentum variation in a lunar month after pre-procession

在“上弦”、“下弦”附近，由于太阳矢量处于xbobzb平面内与+xb轴夹角较小的范围，太阳主要从近似垂直于zb的方向照射，太阳光压角动量累积主要由对中继天线侧面光压力矩产生，以yb轴动量轮角动量持续负向累积为主，xb轴和zb轴角动量累积不明显。在“朔”、“望”附近，由于太阳矢量处于中继卫星星体坐标系-zb或+zb轴附近，对中继卫星呈背面照射(朔)或正面照射(望)，中继天线质量非对称性影响不明显，主要影响来自于星体其它外形结构非对称性、质量分布非对称性、结构器件反光等因素导致的太阳光压心与质心不重合，表现为在星体坐标系三个方向均有力矩，动量轮角动量缓慢累积，累积速度明显低于“上下弦”时yb轴动量轮累积速度。

工程实践中，可通过对单个朔望月周期内的卫星遥测角动量数据进行拟合分析，实现对动量轮卸载时刻和角动量变化的估计；为提高估计准确性，可根据卫星在轨位置、太阳矢量方位和多个周期下传数据对拟合函数进行修正。

拟合函数形式如下：

(8)

式中:T为卫星飞行时对应的朔望月相对时；以当前时刻对应的朔望月相对时和工程实测三轴角动量作为初值，可对式(8)积分计算卫星三轴角动量；当任意一轴角动量达到饱和时(上门限或下门限)，即为预估的动量轮卸载时刻。

3 轨道维持与动量轮卸载联合控制方法

3.1 动量轮卸载角动量变化量与速度增量关系

非力耦姿控发动机执行动量轮卸载时，在产生角速度增量的同时产生速度增量。设发动机推力为F，力臂为l，卫星转动惯量为I，卫星质量为m，则有如下关系：

(9)

可推导得到：

(10)

式中:Δt为姿控发动机喷气工作时长，ΔM为角动量增量，Δv为喷气卸载产生的等效速度增量。可见，根据动量变化量和发动机安装位置可以计算出速度增量。在实际应用中，由于xb和yb方向的耦合关系，理论计算有较大误差。一般可直接采用卸载前后精密定轨结果标定喷气卸载速度增量和卫星角动量变化量之间的关系，即：

Δvd=km(|Dyt-Dy0|+|Dxt-Dx0|)

(11)

式中:Dyt表示卸载前yb轴角动量，Dy0表示卸载后yb轴角动量(标称角动量)，Dxt表示卸载前xb轴角动量，Dx0表示卸载后xb轴角动量(标称角动量)。通过对多次卸载数据进行统计标定得到，km≈0.046，即xb,yb轴单位角动量产生的等效速度增量约0.046 m/s，卸载等效速度增量与卸载角动量呈近似线性关系。因此，若已知卸载时刻及对应的xb,yb轴角动量，可得到卸载喷气产生的等效速度增量大小。

3.2 轨道维持和动量轮卸载联合控制策略

在设计嫦娥四号中继卫星使命轨道维持策略时，若不考虑喷气卸载对轨道构型的扰动影响，会出现构型发散速度不准导致维持周期预估不准的问题，严重时会偏差数天，地面飞控工作中的不确定性大大增加。针对该问题，在前述卸载时刻、卸载方向和卸载喷气等效速度增量估计的基础上，本文提出一种基于维持控制目标偏置的维持和卸载联合控制方法，通过对维持控制和控后动量轮卸载进行联合规划，降低甚至消除动量轮卸载对轨道的扰动影响。具体而言，通过微调轨控开机三方向速度分量ΔV，调整控制目标，即：轨控关机后卫星轨道第三次穿越xrorzr面时xr方向速度v3xr(常规控制策略：v3xr=0)，使得控后第一次卸载后卫星第三次过xrorzr面时xr方向穿越速度v′3xr为0。两种策略比对如表1所示。

表1 常规控制策略和本文控制策略比较Table 1 Comparison of normal and proposed control strategies

本文策略与常规的维持轨控策略的区别在于：常规策略控制目标为维持轨控关机后卫星第三次穿越地月L2旋转坐标系xrorzr面时xr方向穿越速度v3xr为0；而本文提出的联合控制策略，兼顾维持轨控和控后动量轮卸载，控制目标为动量轮卸载后卫星第三次穿越地月L2旋转坐标系xrorzr面时xr方向穿越速度v′3xr为0。对联合控制方法而言，卫星维持控制后第三次穿越地月L2旋转坐标系xrorzr面时xr方向穿越速度v3xr一般不为0，v3xr为待求解量。具体计算步骤如下：

1)建立角动量变化与朔望月时间的拟合函数，确定使命轨道维持控制时机。

3)卸载姿态和卸载喷气等效速度增量计算,根据卸载时刻的卫星位置和月球位置计算得到喷气卸载推力方向矢量n或ni；根据卸载前后xb,yb轴角动量变化量，代入式(11)可得喷气卸载产生的等效速度增量Vi。

4)采用二分法对维持控制目标迭代求解

(1)设置控制目标v3xr搜索区间[V3xrmin,V3xrmax]；

(2)以区间左边界为维持目标v3xr初值，微分改正求解对应的轨控速度增量三方向分量ΔV；

(4)若v′3xr等于0，迭代终止，得到本次维持的控制目标v3xr，否则返回步骤(2)继续迭代。

5)确定维持控制目标和控制量

v′3xr等于0时对应的v3xr即为本次维持控制的目标，对应的速度增量三方向分量ΔV即为本次使命轨道维持轨控开机量。

4 实测轨道校验

以中继卫星某次轨道维持为例，初始轨道历元为2019年2月6日20时。维持前卫星在地月L2点旋转坐标系下的无控外推飞行轨迹如图11所示，轨道动力学模型如表2所示。

表2 Halo轨道动力学模型Table 2 Dynamics model of Halo orbit

图11 中继卫星在地月L2点旋转坐标系xroryr平面 的无控外推飞行轨迹Fig.11 Illustration of flight trajectory in Earth-Moon L2xroryr plane without orbit-keeping maneuver

若不进行使命轨道维持控制，中继卫星飞行轨迹向旋转坐标系-xr方向发散。根据中继需求和测控条件，确定在2019年2月9日20时对中继卫星进行使命轨道维持控制。采用常规控制策略和本文控制策略(维持轨控和控后第一次动量轮卸载联合规划)得到的理论维持计算结果比较情况如表3所示。

采用常规维持控制策略计算得到的中继卫星在地月L2旋转坐标系xroryr平面的理论飞行轨迹(考虑控后1次卸载)如图12所示，采用本文维持控制策略计算得到的中继卫星在地月L2旋转坐标系xroryr平面的理论飞行轨迹(考虑控后1次卸载)如图13所示，两种策略理论飞行轨迹对比效果如图14所示。

表3 常规策略与本文策略理论轨控参数对比Table 3 Comparison of parameters by two methods

工程应用时，由于控制误差、卸载预报误差和后续卸载(每3～4天一次)等影响(折合总误差小于0.012 m/s)，采用联合控制方法对卫星实施使命轨道维持控制后，下一次使命轨道维持控制实际时间为2019年2月22日12时，维持间隔比常规策略理论维持间隔延长约4天，控制量为0.26 m/s。按照正常策略平均8天维持一次计算，联合控制方法一年内可减少维持19次，节省推进剂。

5 结 论

本文针对嫦娥四号中继卫星动量轮喷气卸载对其使命轨道构型的扰动问题，基于工程实测数据定性地分析了动量轮卸载影响以及角动量累积规律，给出了喷气卸载前后角动量变化量与等效速度增量的经验公式。在此基础上，提出了一种使命轨道维持与动量轮卸载联合控制策略，通过对使命轨道维持轨控目标进行偏置，实现卸载后卫星第三次穿越地月L2旋转坐标系xrorzr面时xr方向速度为0，消除控后卸载对使命轨道构型的扰动影响。在高精度力学环境下采用工程应用结果验证了该方法延长中继卫星使命轨道维持控制周期的有效性，可推广应用于GEO卫星和其它类型平动点轨道卫星。由于太阳光压持续周期性的特点，动量轮卸载必须定期进行，所以该方法对有效节约卫星燃料，简化控制流程，减少飞控操作指令，延长卫星使用寿命和空间航天器的在轨管理有十分重要意义，极大地减轻了卫星长期管理工作量。需要指出的是，本文的联合控制方法仅考虑了轨控关机后的一次卸载，后续将对考虑多次卸载的联合控制策略展开研究。

图13 本文方法中继卫星在地月L2点旋转坐标系xroryr 平面理论飞行轨迹(考虑维持后1次卸载)Fig.13 Flight trajectory in Earth-Moon L2xroryr plane with the proposed orbit keeping method and one following uploading

图14 两种策略对比图Fig.14 Illustration of two methods comparison