加锚节理岩体剪切蠕变特性及其本构模型分析
宋 洋,李永启,王韦颐,刘金明
(1.辽宁工程技术大学 建筑与交通学院,辽宁 阜新 123000; 2.辽宁工程技术大学 土木工程学院,辽宁 阜新 123000)
近年来,煤岩的采掘逐渐由原来的浅层向深层发展,在深部巷道掘进、煤岩开挖等过程中,由于煤岩长期受到外荷载作用,破坏形式主要以节理蠕变破坏为主,为研究解决此类问题,需要构建相应的本构模型描述煤岩状态及破坏形式[1-3]。非线性本构模型的建立主要有两种形式:① 通过理论推导,采用损伤力学等相关理论;② 通过室内试验,对原有本构模型进行修正,引入非线性元件代替原有的线性元件[4]。传统的二、三、四元件组合模型仅能描述岩石的弹性或弹黏性,对塑性变形却难以描述。因此,国内外专家、学者通过对原有模型进行改进,用来描述岩石的弹黏塑特性:汪妍妍等[5]通过假定加速蠕变阶段的损伤演化方程,将损伤引入到Burgers模型中,从而提出了一种非线性蠕变损伤模型;吕洪淼等[6]基于Burgers模型引入改进的Kachanov损伤模型,建立描述加速蠕变阶段的蠕变损伤模型,并通过分级加载试验对蠕变本构进行参数反演;杨振伟等[7]基于二维颗粒流程序(PFC2D)中开发出具有黏弹塑性特征的西原体流变接触本构模型,进一步提出包含两种非定常元件的非定常西原体模型,推导了模型本构关系和蠕变方程。
在深部节理岩体中,大多数的岩石失稳发生在蠕变的加速阶段,而现有的Burgers、西原体等相关模型仅能够描述岩石蠕变的瞬态、衰减和稳态阶段,对于加速阶段的塑性变形难以描述,笔者通过引入描述金属材料的Gurson-Tvergaard-Needleman(GTN)损伤模型中屈服方程表征局部塑性剪切区域的塑性变形,将剪切区域定义为塑性剪切破碎带,将其与西原体进行串联,建立起描述加锚节理岩石蠕变全程的非线性复合流变模型,采用MIMICS软件对CT得到的扫描图进行三维重构,求解模型相关参数,并通过试验与拟合对比,说明复合流变模型的合理性,为深部岩体剪切蠕变的研究提供方法。
1 试验概况
1.1 试件制作及试验设备
试验选取相似材料模拟岩石属性,通过对不同配合比下试件进行单轴压缩试验,选择配合比为水泥∶河砂∶水=1∶1.5∶0.4制作试件,其抗压强度为20 MPa;锚杆材料选用Q235型光圆钢筋,直径为8 mm,长度为100 mm,屈服强度为235 MPa。模型整体为边长100 mm正方体试件,节理部分采用水泥砂浆浇筑成100 mm×100 mm×5 mm的长方体,其中节理厚度为5 mm,试验过程中保证节理形状、尺寸、材料配比一致,节理试件实物示意图如图1所示。本次试验锚杆锚固方式为全长式锚固,将锚固节理试件作为一个完整体进行实验,实验结果只针对本条件的试件得出。

图1 节理试件实物示意Fig.1 Physical sketch of joint specimen
1.2 试验方案
本次试验加载系统采用辽宁工程技术大学土木工程试验中心的TAW2000三轴试验仪的剪切装置,如图2中标记所示,将剪切装置推到仪器正下方,通过电脑控制施加不同法向应力,并推动剪切上盘进行试件的剪切蠕变试验。由于分级加载方法可以在同一试样上观测不同应力水平的变形规律,大大节省了试验研究所需的试样和试验仪器的数量,同时还可以避免因为试样性质不均匀性导致的试验数据的离散性等,因此试验采用分级加载的方式,将试验分级划分为6级加载,分级为试件抗压强度的15%,30%,45%,60%,75%,90%,即试件初始剪切应力与应力增量均为3 MPa。
试件安装完毕后,对试件施加轴向荷载,待法向应力稳定后,从低到高逐级施加水平剪切应力,待每级施加后,立即测量、读取瞬时位移,然后按5,10,20,40 min,1,2,4,8,12 h时间间隔读取衰减和稳态阶段剪切蠕变值,此后每隔12 h读取1次,试验每级荷载维持5 d左右,岩石剪切蠕变变形稳定的条件为蠕变速率增量≤5×10-4mm/d,对于加速蠕变阶段,考虑到蠕变变形较大、蠕变时间较快,每隔5 min读取1次数据,直至试件破坏。对试件进行轴向荷载分别为1,2,3 kN下的剪切蠕变试验。

图2 节理岩体试块剪切装置Fig.2 Shear device for jointed rock block
1.3 试验结果及分析
在试验结果中每组选取一个具有代表性的试件进行分析,通过对试验数据进行分析和整理,得到剪切蠕变试验曲线如图3所示。

图3 不同法向应力下剪切蠕变曲线Fig.3 Shear creep curves under different normal stresses
由图3可知,采用相似材料模拟节理岩体剪切蠕变试验曲线有如下特征:
(1)试样在剪切蠕变过程中,表现出典型的蠕变特征:① 衰减蠕变阶段,蠕变速率减小,如图3(a)中第1级水平剪切荷载施加后0~0.7 d的蠕变阶段;② 稳态蠕变阶段,蠕变速率大致保持恒定并近似为0,如图3(a)中第2级水平剪切荷载施加后6~10 d的蠕变阶段;③ 亚稳态蠕变阶段,蠕变速率近似恒定且大于0,如图3(b)中第5级水平剪切荷载施加后21~25 d的蠕变阶段;④ 加速蠕变阶段,蠕变速率快速增加,如图3(c)中第6级水平剪切荷载施加后30~32 d内的蠕变阶段。
(2)通过对不同法向应力下的瞬时蠕变变形和衰减蠕变时间进行统计分析,由图4可知:随着法向应力的增加,瞬时蠕变变形量呈现逐渐递减的变化趋势,当法向应力由0.1 MPa变化到0.3 MPa时,瞬时蠕变变形下降了约75%。其原因为:当法向应力增大时,试件抵抗剪切变形的能力就越强,说明正应力的增加提高了试件的延性特性;而衰减蠕变时间与法向应力出现同步变化的趋势,随着法向应力的增加而延长,当法向应力由0.1 MPa变化到0.3 MPa时,衰减蠕变时间增加约50%,究其原因为:随着法向应力的增大,试件抵抗蠕变变形的能力随之提高,从而导致衰减蠕变变形的时间延长。
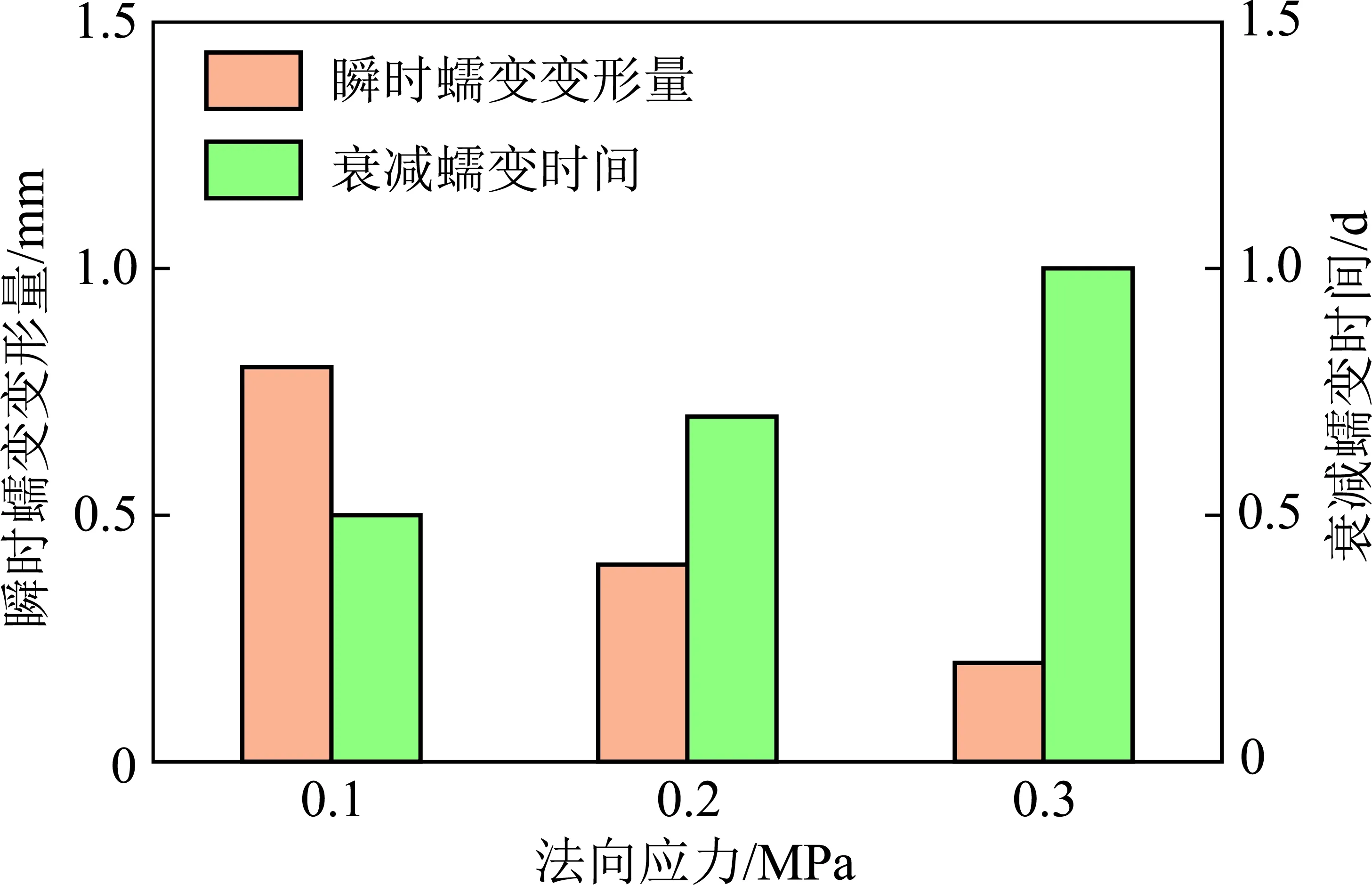
图4 蠕变时间柱状Fig.4 Creep time histogram
(3)为描述剪切蠕变过程中的稳态蠕变阶段,现将不同法向应力下稳态蠕变时间和试件破坏时间统计见表1。
表1 试件时间统计
Table 1 Statistical table of sample time
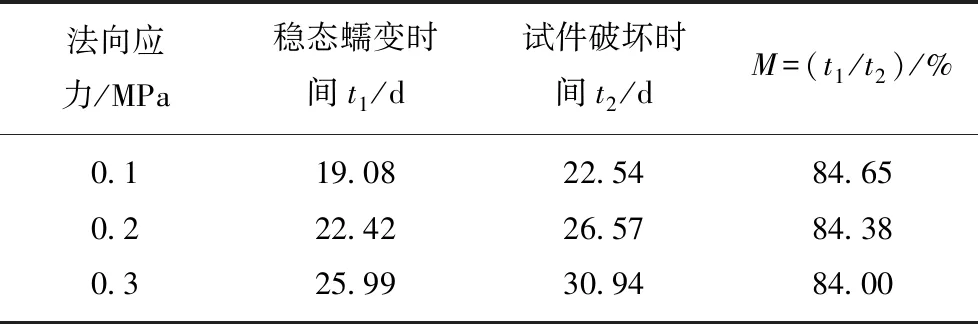
法向应力/MPa稳态蠕变时间t1/d试件破坏时间t2/dM=(t1/t2)/%0.119.0822.5484.650.222.4226.5784.380.325.9930.9484.00
由表1可知:随着法向应力的增加,试件的稳态蠕变时间和试件破坏时间均呈现出上升的趋势,说明法向应力的增加,提高了岩石的延性特性,延缓了试件的破坏时间;表1中M为稳态蠕变时间与试件破坏时间的比值,设为时间因数,从表中可以看出,时间因数M均大于84%,说明稳态蠕变时间在整个试件破坏过程中占比较大;同时,时间因数M不随法向应力等外力的增加而变化,近似为恒定值,则可认为在各级剪切应力为岩石强度6等分级下,即各级增量为岩石强度15%下进行分级,时间因数M为剪切蠕变过程中试件的固有属性。
为更好研究时间因数M,通过参考相关资料[8-10]对不同岩石的时间因数M和孔隙体积分数f进行统计,见表2,表中,f为试件到达加速阶段时孔隙体积分数增量,f相关求解步骤见4.2节,f=fb-fa,fb为试件在加速阶段开始时孔隙体积分数;fa为试件初始孔隙体积分数。由于试件初始孔隙体积分数fa较小,近似为0,则取f=fb进行简便计算。
表2 不同岩石的时间因数M统计
Table 2 Statistical table of time factorMfor different rocks
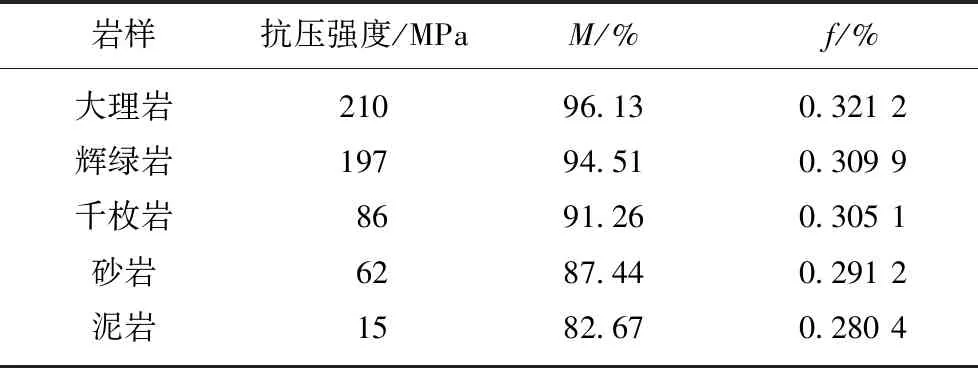
岩样抗压强度/MPaM/%f/%大理岩21096.130.321 2辉绿岩19794.510.309 9千枚岩8691.260.305 1砂岩6287.440.291 2泥岩1582.670.280 4
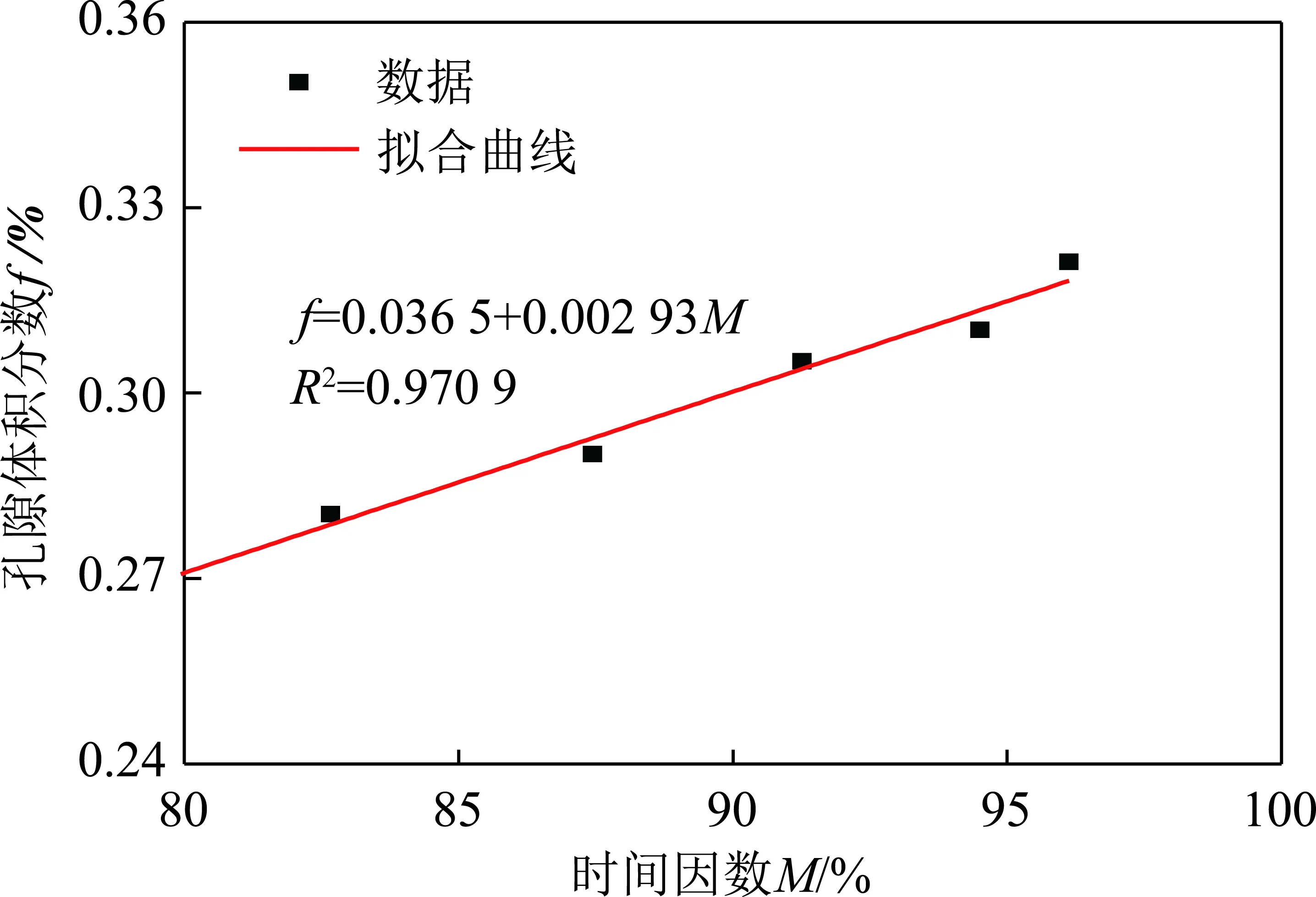
图5 孔隙体积分数随时间因数变化曲线Fig.5 Pore volume fraction versus time factor curve
由表2可知,不同岩性的岩样试件具有不同的时间因数M,从而也表明时间因数M为岩石的特性,并且时间因数M随着试件抗压强度的提高而呈现增加的趋势,当岩石的抗压强度由210 MPa下降到15 MPa,降幅近93%,而相对应的时间因数M下降幅度则相对较小,仅为14%,由此说明:相对于岩石抗压强度的变化幅度,时间因数M则相对固定,变化范围较小,更具有稳定性。
对不同时间因数M下的孔隙体积分数f变化绘制成图5,由图5可知,曲线呈近似线性变化,说明对于给定的时间因数M,对应有惟一确定的孔隙体积分数与之对应,可以根据剪切蠕变曲线确定时间因数M取值,从而利用线性关系找出对应的孔隙体积分数f,则可以实现对节理岩体塑性剪切破碎带中孔隙或裂隙的定量表征。
2 剪切蠕变特性分析
2.1 长期强度
为求解试件的长期强度,通过对图3采用Boltzmann叠加原理,以每级相同时间间隔为参数,绘制不同法向应力下剪切应力-位移的等时曲线簇,其中0 d为每级剪切应力施加时的相对起始时间,如图6所示。
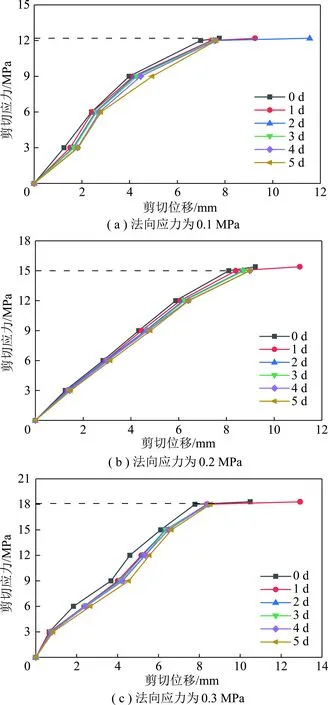
图6 剪切蠕变等时簇曲线 Fig 6 Isochronic cluster curves of shear creep
由图6可知,不同法向应力下试件的长期强度不同,当法向应力分别为0.1,0.2,0.3 MPa时,其长期强度分别为12.2,15.0,18.1 MPa,曲线在长期强度之前近似为线性变化,随着剪切应力的增加,剪切位移逐渐变大,试件裂隙经历了由闭合到扩展的过程;而当剪应力大于长期强度后,曲线近似呈现水平,其原因为随着剪切应力水平的增大,岩体抵抗变形的能力降低,当超过剪切强度时,试件已经发生破坏,岩体失去抵抗剪切的能力,从而出现当剪切应力恒定时,剪切位移随时间而变化的现象。
2.2 蠕变速率
为更好研究剪切蠕变全程,以0.1 MPa法向应力为例,绘制蠕变速率随时间变化曲线,如图7所示,由图7可知,不同蠕变速率随着时间呈现先急剧下降而后逐渐接近于某一定值的趋势,当时间一定时,随着剪应力水平的提高,蠕变速率增加,分析可知:蠕变速率描述的是单位时间内的蠕变量,剪应力越大,在相同法向应力下的剪切位移就越大;在衰减蠕变阶段,蠕变速率随时间呈现断崖式下降,原因为:在剪切蠕变初期,由于岩石具有抵抗剪切破坏的能力,使得蠕变速率大幅度下降;在稳态或亚稳态蠕变阶段,蠕变速率曲线下降速度减慢,逐渐趋向于0,在此阶段,节理裂隙逐渐发育、扩展,由于试件抵抗剪切破坏能力的逐渐下降,使试件中裂隙的发育速度降低,直至为0;在加速蠕变阶段,试件发生新生裂隙的贯通,蠕变速率上升,曲线近似呈现“U”形。
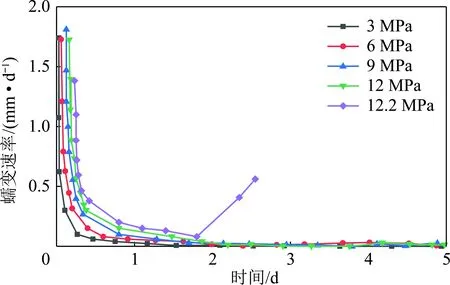
图7 蠕变速率-时间曲线Fig.7 Creep rate time curves
2.3 剪切模量
为了定量描述剪切模量随时间的变化,以法向应力0.3 MPa为例,取各相对时刻下不同剪应力水平和与之对应的应变来进行线性回归,拟合出直线的斜率即为对应的剪切模量,整理出各时刻对应的剪切模量绘制拟合曲线如图8所示。
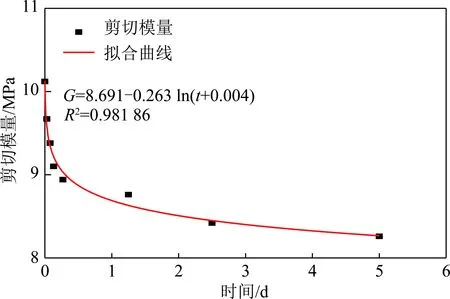
图8 剪切模量-时间关系曲线Fig.8 Time-dependent curve of shear modulus
由图8可知:剪切模量随时间的推移逐渐变小,并且其减小的速率也越来越小,逐渐趋于恒定,采用对数函数对其进行拟合,其拟合系数R2为0.981 86,说明拟合效果较好,能够用对数函数描述剪切模量随时间的变化关系。
3 本构模型
3.1 模型选择
深部节理岩体的破坏主要是围绕着塑性剪切破碎带进行的,但是现有原件及其组合对于节理岩体的非线性破坏阶段不能较好的描述,而确定岩石进入加速阶段的临界剪切强度对于岩石的破坏来说至关重要。因此,如何引入元件来描述加速阶段及岩石塑性区变化就成为重点,笔者通过引入复合材料中GTN元件模型,与西原体串联来描述岩石剪切破坏的全过程。采用GTN模型的原因如下:① GTN模型始于金属材料,用来描述金属材料由于内部出现孔隙扩展、汇聚而引起材料韧性变形的现象。而韧性变形是指物体发生明显的应变(大于5%)才发生破裂的变形。可用韧性变形表述岩石的流动变形现象,其具体变形机制包括碎裂流动、塑性流动和滑移流动等[11],由图3可知,试件变形为5.22,5.4,5.8 mm,平均应变为5.47%,大于韧性变形的起始值;② GTN模型能够较好描述金属材料塑性变形,可以用来描述金属材料锚杆与岩石在剪切蠕变全程中的耦合作用;③ GTN模型属于各向异性的本构模型,与岩石性质一致。综上所述,能够通过引入GTN模型对岩石剪切蠕变进行描述[12]。
GTN模型的屈服函数Φ(q,p,σm,f*)表达式[13-14]如下:

(1)
式中,p为静水应力;q为von Mises等效应力;σm为基体材料的屈服应力;q1,q2,q3为由Tvergaard[14]考虑孔隙聚合作用引入的模型校准参数;f*为有效孔隙体积分数,是孔隙体积分数f的函数,其表达式为
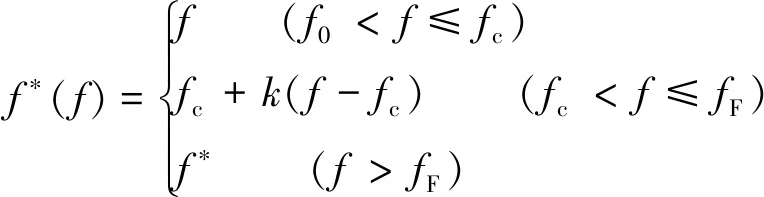
(2)
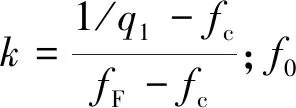
由于考虑到本次采用GTN模型是用来描述岩石剪切蠕变的稳态阶段后期和加速阶段,即从裂隙开始发育、贯通到试件出现宏观裂隙。所以,本文选取有效孔隙体积分数为

(3)
3.2 复合流变模型
(1)GNT屈服函数

(4)
(2)改进的西原体
将传统西原模型[15-17]与GTN模型进行串联得到复合流变模型如图9所示。

图9 复合流变模型Fig.9 Compound rheological model
模型总应变为
ε=εB+εK+εGTN
(5)
式中,εB为宾厄姆体的应变;εK为凯尔文体的应变;εGTN为GTN模型的应变。
将式(1)~(4)进行积分求解后代入式(5),可以得到描述含有一定厚度填充物下加锚节理岩体复合流变模型的蠕变方程:
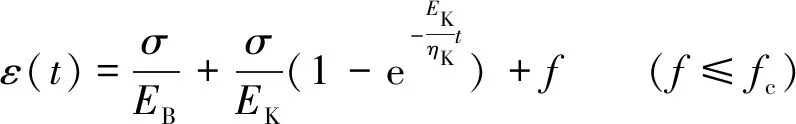
(6)
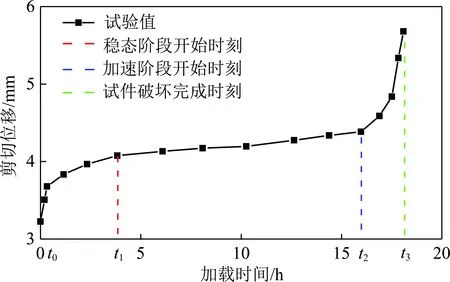
(fc (7) (fc (8) 式中,EB,EK分别为宾厄姆体和凯尔文体的弹性模量;ηB,ηK分别为宾厄姆体和凯尔文体的黏滞系数;σs为模型的长期强度;p=σij/3为复合流变模型总应力;p=σij/3为施加应力。 当引入GTN后,岩体剪切蠕变本构方程演化为式(8),该式描述环境为试件应力大于长期强度且孔洞处于聚合与破坏之间时,即试件处于加速阶段;当试件应力小于长期强度但孔洞仍处于聚合与破坏之间时,式(8)退化为式(7),即试件处于稳态或亚稳态阶段;当试件孔洞小于聚合时,式(7)退化为式(6),即试件处在衰减阶段,试件稳定无新裂隙产生。所以,式(6)~(8)为岩石复合流变模型的蠕变方程,不仅可以描述岩体的弹黏性阶段,而且由于引入GTN模型,使该模型能够描述加锚节理岩体的加速蠕变变形。 GTN模型中需要确定9个参数,将其可分为3类[13]:①q1,q2,q3为孔隙间相互作用参数,对于金属材料来说,考虑孔隙周围非均匀应力场和相邻孔隙之间的相互作用,取q1=1.5,q2=1.0,q3=2.25。②f0,sn,εn和fn为材料孔隙体积分数参数,其中,f0为初始孔隙体积分数;sn为孔隙体积分数的离散程度,一般取0.1;εn为塑性应变水平,一般取0.3[13];fn为控制损伤的演化率。③fc和fF为韧性断裂参数,其中,fc控制累计孔隙体积分数的增长,fF控制材料的断裂,其中部分已知参数见表3。 表3 GTN模型适用参数 参数q1q2q3snεn数值1.51.02.250.10.3 (1)静水应力p: p=σij/3,σij=(σ11+σ22+σ33)/3 式中,σij为材料应力,代入得p=0.1 MPa。 (2)von Mises等效应力q: 式中,sij为柯西应力的偏应力分量;δij为克罗内克记号,代入上式得等效应力为10.5 MPa。 (3)基体材料的屈服应力σm: 为求解GTN模型参数,取法向应力0.3 MPa作用下,剪切应力为18.3 MPa时的剪切蠕变试验结果绘制如图10所示,等效应力采用SWIFT H W[18]强化模型对剪切试验曲线初期阶段进行拟合求解,其表达式为 σm=k(ε0+ε)n (9) 式中,k,ε0为材料参数;n为硬化指数。 图10 剪切蠕变曲线 Fig 10 Shear creep curve 通过对图10中(t0-t1)时刻剪切蠕变曲线初期阶段进行拟合,拟合得到k=52.79,ε0=0.198,n=0.36,将参数代入式(9)得 σm=52.79(0.198+ε)0.36 (10) 并取t1时刻的应变代入式(8)得到基体材料的屈服应力为0.229 MPa。 孔隙体积分数表示均质或非均质材料内部微孔隙的体积占材料总体积的百分比,是一种外力加载下材料损伤的具体形式。以求解fF为例,说明不同孔隙体积分数的求解步骤: (1)确定各孔隙体积分数对应的岩石试件的剪切蠕变状态,如fF试件在加速阶段开始时孔隙体积分数; (2)对确定好蠕变状态的试件进行CT扫描,每个图层间隔为100 μm,塑性剪切破碎带约为2 cm,共有扫描图层200个; (3)利用Matlab图像处理软件对CT图进行二值化处理,通过调节阈值,找到节理剪切破碎带中每隔100 μm对试件进行CT扫描的清晰图像,从试件下盘向上依次如图11中(a)~(i)所示; (4)将处理后的图像导入三维重构软件,基于商业三维重构软件Mimics和开源软件Image J对图片中的裂隙进行标记、分割和三维特征参数的测量,图12为试件塑性剪切破碎带的三维重构图,其中黄色部分为裂隙或孔隙,绿色部分为试件,通过测算得到孔隙体积分数,作为宏观破坏时的孔隙体积分数fF。 通过上述步骤对试件的不同阶段进行处理,利用对时间因数M的不同取值,得到不同孔隙体积分数,见表4。 4.3.1元件参数求解 利用岩石剪切蠕变破坏阶段的应变-时间曲线,根据4.2节步骤(1),(2)可求得式(6)~(8)中的相关元件参数,见表5。 图11 Matlab处理图Fig.11 Matlab processing diagram 图12 三维MIMICS重构 Fig 12 Three-dimensional MIMICS reconstruction 表4 不同孔隙体积分数 f0fcfFfn0.0010.10.120.04 表5 模型试验参数识别 参数EBEKηBηKσs/MPa数值2.81×1060.0210.0010.0218.1 (1)确定EB,由式(6)可知,当t=0时,ε(0)=σ(0)/EB,而σ(0)=0.3 MPa,ε(0)可由岩石剪切流变试验曲线得到,可得EB=σ(0)/ε(0)。 (2)确定σs,由图(8)可知,0.3 MPa法向应力下对应的试件剪切蠕变的长期强度为18.1 MPa。 4.3.2有效孔隙体积分数的系数求解 由于加速段为非线性变化,且幂指函数的自身特点也更加符合加速蠕变的规律,所以令: (11) 将式(11)代入到式(8)中得到 (12) 将表3~5中系数代入式(12),利用数学优化软件1stOpt,基于准牛顿法和通用全局优化法对图10中t2~t3时间段的试验值进行参数识别,可求EK,ηB,ηK的值见表5,得到有效孔隙体积分数的相关系数见表6。 表6 有效孔隙体积分数的系数 系数abc数值24.11.462.13 利用传统西原模型、复合流变模型分别拟合不同法向应力下岩石剪切蠕变过程曲线,结果如图13所示,并对两种模型不同时刻曲线的拟合系数进行对比,见表7。 图13 蠕变模型数值拟合结果与试验结果对比 Fig 13 Comparison of numerical fitting results of creep model with experimental results 表7 模型不同阶段拟合系数 法向应力/MPa蠕变模型R21R22R230.1传统西原模型1.01.00.623 82复合流变模型1.01.00.962 740.2传统西原模型1.01.00.611 94复合流变模型1.01.00.951 360.3传统西原模型1.01.00.646 54复合流变模型1.01.00.954 82 (1)在加锚节理岩体剪切蠕变试验中,岩石瞬时蠕变变形量和衰减蠕变时间随法向应力线性变化,且瞬时蠕变变形量与应力呈负相关,衰减蠕变时间与应力呈正相关。 (2)通过绘制不同法向应力下剪切应力-位移的等时曲线簇,得到试件长期强度的相关规律:试件长期强度随法向应力的提高而增加,其原因为法向应力的提高,增加了试件的延性,从而增强试件抵抗剪切变形的能力,使试件长期强度提高。 (3)通过对不同试件剪切蠕变分析,说明时间因数M为岩石固有属性,且时间因数M随着岩石强度的增加而提高;通过时间因数M,能够得到岩石相应孔隙体积分数f,从而实现对岩石裂隙的定量描述。 (4)通过在传统西原模型基础上串联GTN模型,得到能够描述岩石弹黏塑性变化全程的复合流变模型,通过验证、对比可知,复合流变模型与传统西原体均可描述岩石剪切蠕变的衰减、稳态阶段,但复合流变模型能更好的分析试件加速阶段,以定量分析的方式研究试件的破坏,从而为深部加锚节理岩体的研究提供理论支撑。4 参数识别
Table 3 Applicable parameters of GTN model
4.1 GTN屈服函数参数识别
4.2 孔隙体积分数求解
4.3 试验参数识别


Table 4 Volume fraction of different voids
Table 5 Identification of model test parameters
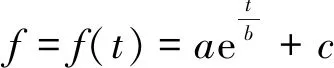

Table 6 Coefficient of effective void volume fraction
4.4 拟合结果分析
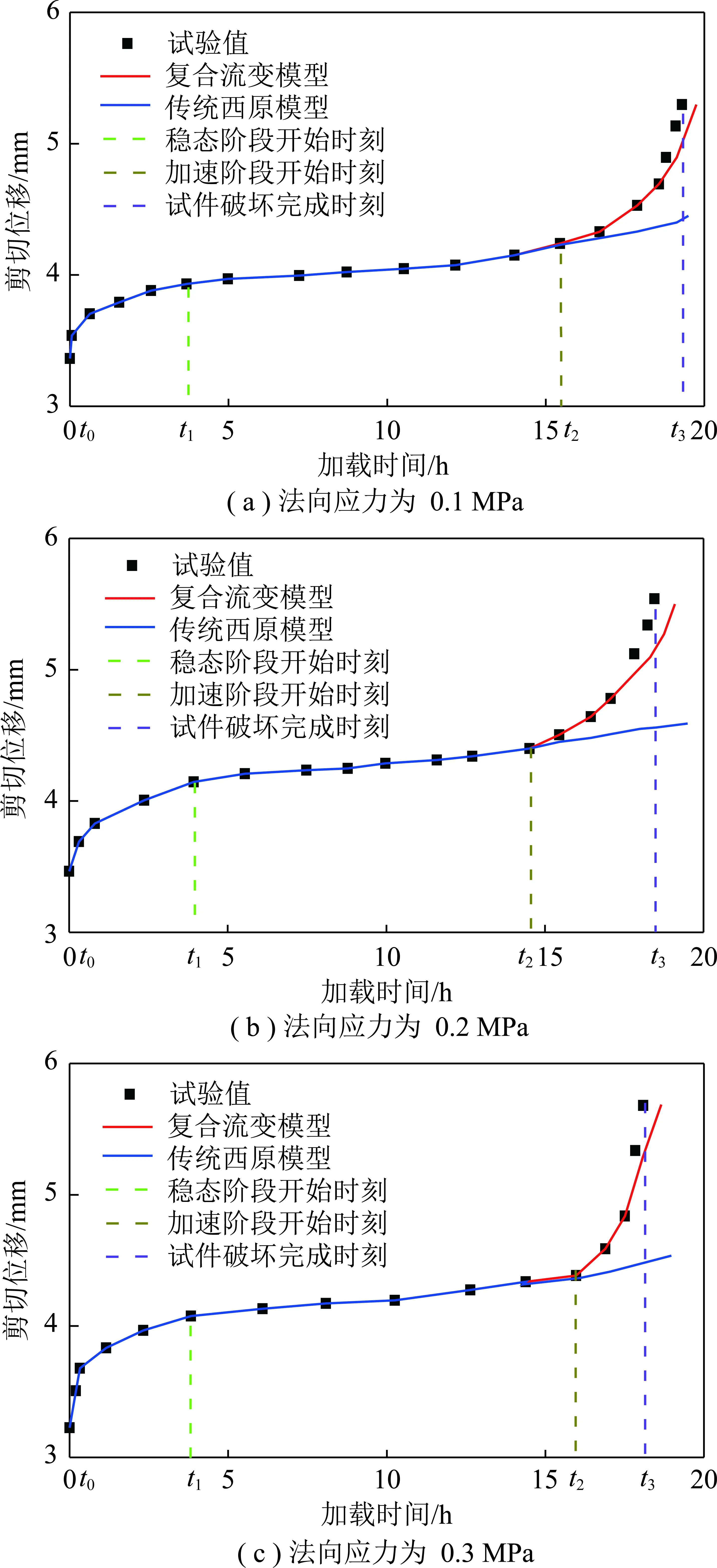
Table 7 Fitting coefficient for different stages of model
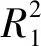
5 结 论

