蠕变作用下埋深对结构受荷特征影响分析——以广佛环线东环隧道工程为例

周 坤，陈 龙

(1.中铁第四勘察设计院集团有限公司，武汉 430063；2.西南交通大学交通隧道工程教育部重点实验室，成都 610031)

近年来，伴随着中国经济水平的飞速发展和隧道工程施工工艺技术的进步，中国已经成为当今世界上隧道及地下工程规模最大、数量最多、地质条件和结构形式最复杂、修建技术发展速度最快的国家[1]。

基于此，以广州东环隧道为背景，运用FLAC3D有限差分软件研究蠕变作用下埋深是如何影响管片衬砌的变形和受力特性，以期对后续深埋软岩隧道的长期受荷和变形取值提供经验和依据。

1 工程概况

依托广佛环线广州南站至白云机场段东环隧道大源站—太和站区间盾构隧道工程展开相关研究工作。该项目位于珠江三角洲中部，西连佛肇城际，东接佛莞城际，同时衔接佛莞线、穗莞深线、广惠线、广清线、佛肇线和广佛江珠6条城际线路，是珠三角城际轨道交通网及广佛环线的重要组成部分。其中，广佛东环隧道大源站—太和站区间隧道工程位于广州市白云区太和镇，为双线铁路隧道，隧道主要采用盾构法施工，建筑长度6 804 m，区间盾构隧道总长5 987 m。隧道主体结构采用单层装配式通用管片环，混凝土强度等级为C50，抗渗等级P12。管片衬砌外直径8.8 m，厚400 mm，环宽1.8 m，采用“6+1”分块模式，具体为4B(56.84°)+2L(56.84°)+F(18.96)，其中B为标准块，L为邻接块，F为封顶块，管片结构分块情况如图1所示。

图1 盾构法隧道管片结构分块图Fig.1 Block diagram of shield tunnel structure

依托工程隧址区多为丘陵与丘间谷地，属丘陵地貌，地势起伏较大，地面高程21～135 m，隧道埋深十余米至上百米不等，最大覆土厚度超过130 m。其中盾构隧道长距离下穿不同风化程度的片麻岩、炭质板岩、粉砂岩、泥质砂岩等，围岩风化程度高、强度差异较大、渗透性差异显著，为目前中国首次采用盾构隧道的方式长距离穿越大埋深岩层，区间隧道地质纵断面如图2所示。

图2 隧道穿越岩层断面图Fig.2 Cross section of tunnel through rock formation

2 数值分析模型

对于大埋深软岩盾构隧道，在地应力作用下当岩体发生持续的流变行为特征后，隧道开挖后围岩的塑性区范围会进一步发展，管片结构所承受的围岩形变压力随时间变化而逐渐增大，进而导致将结构变形和内力的增加。因此，利用数值仿真的方法研究围岩蠕变作用下不同埋深软岩盾构隧道结构受荷特征。

2.1 基本假定

结合FLAC3D有限差分软件的功能特征，在进行模型建立和荷载分析时做如下假定。

(1)不考虑深埋岩体的各项异形特征，将隧道围岩视为结构部均匀的各项同性连续介质。

(2)模型中不考虑地下水对盾构隧道结构的荷载作用和对围岩力学特性软化的影响，取自然含水状态岩石力学参数为计算参数。

(3)现场得到的岩体试样室内力学试验的结果都是可信的，可以反映在地应力条件下的应力特征，且根据试验结果的岩体参数可以用于数值模型中。

(4)对于所考虑的隧道埋深情况，建立模型时只考虑地层的自重应力场。

(5)盾构隧道每一施工步的时间较短，岩体实际发生蠕变行为较弱，因此在建立模型时不考虑盾构隧道每一施工步的围岩蠕变行为，仅考虑盾构隧道开挖完成后的围岩长期蠕变行为。

2.2 数值模型

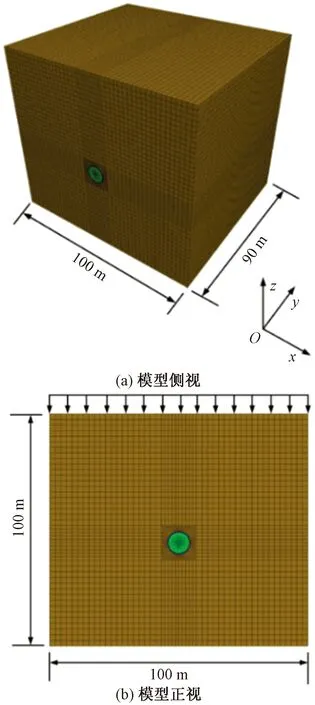
图3 数值计算分析整体模型Fig.3 Numerical calculation analysis of the overall model

在2.1节合理假设的基础上，利用FLAC3D软件建立考虑盾构施工过程的大埋深隧道三维数值模型如图3所示。一般认为数值模型边界与隧道边界的距离取其洞径的3倍以上时可不考虑模型边界效应影响，因此建模时为了减小模型计算的边界效应，取隧道中心与模型四周边界的距离均为50 m，在模型纵向上考虑盾构开挖及管片衬砌施作的施工过程影响取纵向距离为90 m(50环)，即计算模型的尺寸为100 m(x)×100 m(z)×90 m(y)。边界条件中模型四周及底面采用法相位移约束条件，并考虑隧道埋深条件和地应力场分布在模型上表面和模型内部单元施加相应的构造应力以模型地层真实的自重应力场。

2.3 模型相关参数

2.3.1 隧道围岩参数

数值模型中隧道围岩采用正六面体实体单元模拟，根据假定条件在模拟盾构隧道施工过程中不考虑围岩蠕变特性，则岩体为理想弹塑性体，遵循Mohr-Coulomb屈服准则。在模拟围岩长期蠕变行为时，岩体的蠕变模型采用FLAC3D软件中可以模拟岩土体黏弹、黏性、黏塑行为的Cvisc模型。计算模型中所采用围岩力学参数如表1所示。

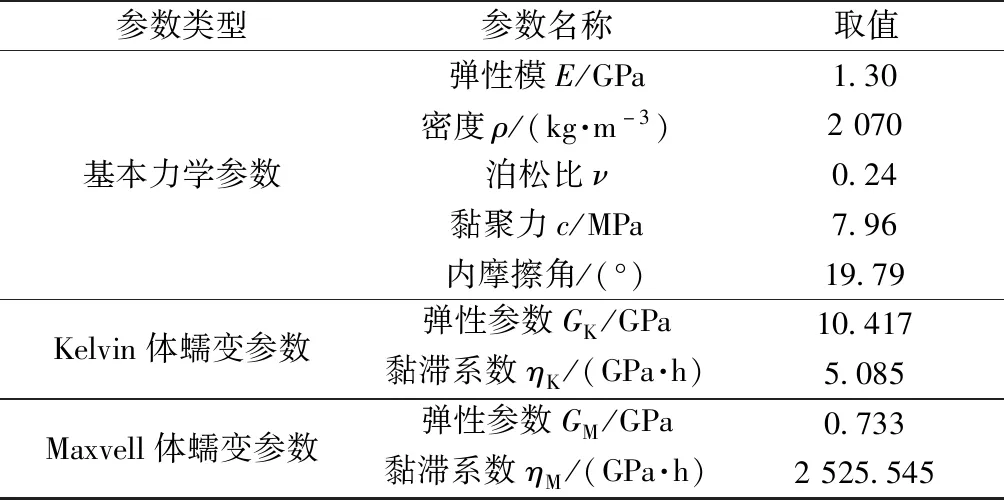
表1 隧道围岩计算力学参数Table 1 Calculation of mechanical parameters of tunnel surrounding rock

2.3.2 盾构隧道相关组参数

为了对盾构隧道的施工过程进行模拟，数值模型中分别对与盾构掘进施工相关的主要结构构件进行了模拟。依托工程广佛环线东环隧道的盾构机结构如图4所示，其中盾壳分前盾、中盾、和后盾三部分，各部分的半径依次略有缩小，盾壳整体呈锥形特征分布，而建模时做简化处理，将其考虑为圆柱形结构。盾构隧道主要结构构件的参数如表2所示。

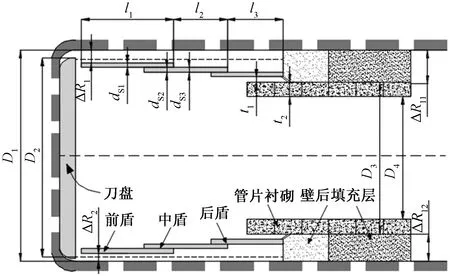
图4 依托工程盾构机形式示意图Fig.4 Schematic diagram of the form of the shield machine

2.3.3 层间模拟及接触面接触参数

(1)interface界面单元基本理论：图5为FLAC3D软件中interface界面单元、节点和节点接触面积和本构模型的示意图，其中Kn为法向刚度，Ks为剪切模量，每一个四边形的区域都有两个接触单元定义，接触面本构关系服从Coulomb抗剪强度准则。

表2 盾构主要结构组件的几何尺寸Table 2 Geometric dimensions of the main structural components of the shield

在利用FLAC3D软件中的接触单元进行计算时，interface接触面的节点会对接触面的变形进行探测，并通过图5所示的本构关系来表示接触面单元的实际关系，其中法向刚度Kn和剪切刚度Ks是表示接触面单元特征的重要参数。Kn和Ks取值过大会导致计算响应和收敛速度慢，并可能产生与相关的数值误差。FLAC3D软件的用户手册中给出了法向刚度Kn和剪切刚度Ks的经验选取方法[15]。

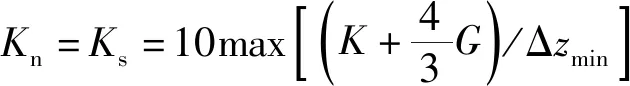
(1)

式(1)中：K为体积模量；Kn为法向刚度；Ks为剪切刚度；G为剪切模量；Δzmin为接触面法向方向上连续区域的最小尺寸。

(2)模型中的接触面单元：计算模型中，刀盘的扩挖使得盾构机盾壳与隧道围岩之间存在超挖间隙，为了模拟出盾构超挖作用对围岩土体的卸荷作用，在层间设置了接触单元。为了求得管片结构所受到的围岩荷载作用，在管片与壁后注浆层之间设置了层间接触单元。两处的层间接触单元都采用FLAC3D软件中的interface接触单元模拟，且根据软件中接触面单元的特点和要求，将接触面应连接到密度较大的网格上，得到计算模型中的接触面如图6所示。

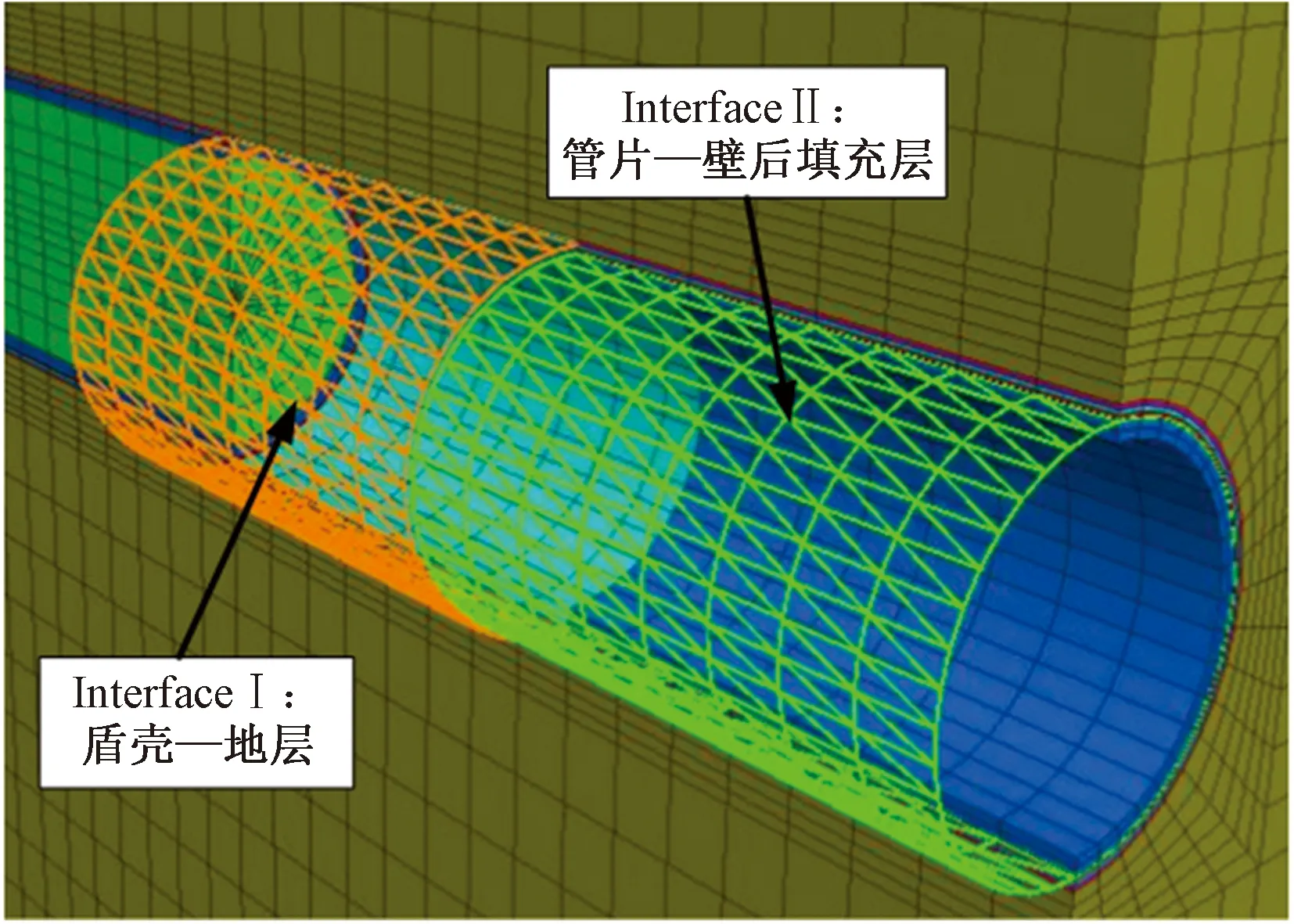
图6 计算模型中的接触面单元Fig.6 Contact surface unit in the calculation model

2.3.4 计算模拟流程

利用数值模型进行数值计算时，根据施工阶段对盾构隧道的施工全过程进行模拟。相应的施工模拟过程及计算步骤如下。

Step1计算初始地应力场。根据隧道埋深对模型施加地层自重应力场，设置模型边界条件，进行平衡计算。

Step2盾构进洞计算模拟。在模型中进行盾构掘进和土体开挖模拟，施加掌子面推力并激活盾壳单元与盾壳处接触面单元，模拟盾构机的进洞行为。这一阶段过程如图7(a)所示。

Step3盾构隧道正常掘进施工模拟。待盾壳完成进入地层即盾构机完成进洞行为后，模拟盾构机向前推进过程，同时激活盾构管片和壁后注浆层单元。这一阶段过程如图7(b)所示。

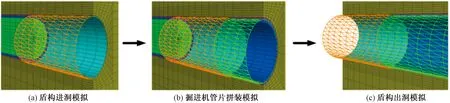
图7 盾构隧道施工模拟示意图Fig.7 Schematic diagram of shield tunnel construction simulation

Step4盾构隧道出洞模拟。待模型中盾壳到达模型边界时，盾构继续推进，并在盾尾激活管片和填充层单元直至完成全部管片拼装模拟。过程如图7(c)所示。

图8 不同埋深下管片衬砌径向变形Fig.8 Radial deformation of segment lining under different buried depths

Step5围岩蠕变行为模拟。将模型中围岩土体设置为Cvisc模型，赋予表1中的岩体蠕变参数，进行蠕变计算。蠕变计算时首先需要打开FLAC3D软件中的蠕变计算模块，并设置蠕变计算的时间步长等量值。利用FLAC3D软件进行蠕变计算分析时的详细理论可以参考文献[19]。

3 不同埋深下结构受荷特征分析

在仅考虑岩体自重应力场的情况下，随着埋深的增大岩体赋存环境的地应力越大，隧道开挖后围岩的变形和应力作用越明显。在考虑围岩蠕变效应的情况下，地层应力越大，岩体在应力作用下产生的蠕变变形越大，且当地层应力超过岩体的强度限制时，隧道开挖后围岩将发生加速蠕变行为，从而对隧道支护结构产生危害。鉴于此，结合依托项目的工特点，研究蠕变作用下隧道不同埋深对结构受荷特性的影响，设计了埋深h=60、80、100、120、150、200 m工况进行分析。

3.1 模型相关参数

根据数值结果得到围岩蠕变时间t为0、5、50、100 a后不同隧道埋深下管片衬砌的径向变形，如图8所示(径向变形量值以向管片外侧为正，向内侧为负)。

前者生成的空调系统在设备特征中存在数据理想化的问题，在管路布置中存在偏差。接下来，分别对两者进行修正，并对系统进行图示化处理。

由图8可知，随埋深的增大，管片衬砌整体变形更加显著，变形趋于不利。当不考虑围岩蠕变效应时(t=0)，随埋深增大，管片衬砌拱顶沉降逐渐增加，拱底隆起变形逐渐增大；考虑围岩蠕变效应后，管片衬砌整体发生沿竖向向下的变形，拱底由隆起变形而逐渐变为沉降变形。

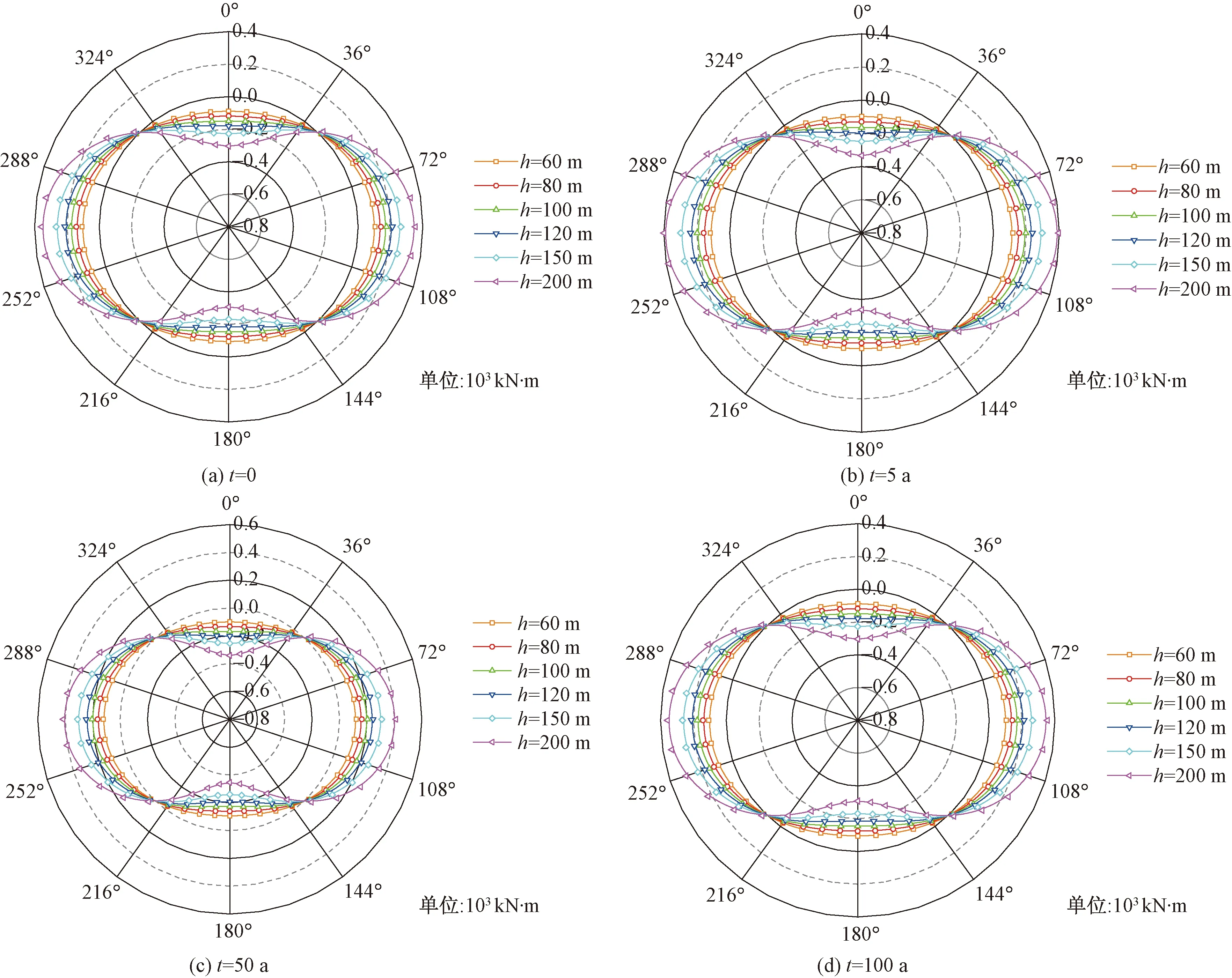
图9 不同埋深下管片衬砌弯矩分布Fig.9 Distribution of bending moment of segment lining under different buried depths

现以拱顶竖向位移为例，得到围岩蠕变5 a和100 a时位移的变化情况如表3所示。由表3可知，围岩衰减蠕变阶段拱顶竖向位移变化率远大于稳定蠕变阶段，围岩蠕变过程中管片衬砌位移的变化率随着埋深的增加逐渐增大，埋深越大管片衬砌的变形发展越显著。

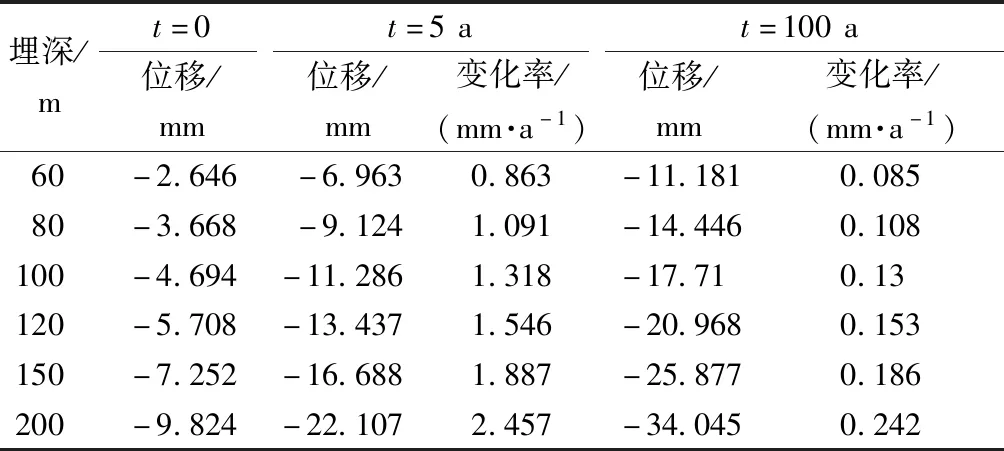
表3 各工况下拱顶竖向位移变化情况Table 3 Changes in vertical displacement of the dome under various working conditions

3.2 管片结构内力分析

弯矩和轴力是进行结构受力分析常用的量值，通过FLAC3D内置的Fish语言提取围岩蠕变过程中不同埋深隧道管片衬砌的弯矩如图9所示。

如图9所示，在各个计算工况下管片衬砌的弯矩分布规律基本相同，即拱顶和拱底受负弯矩，两侧拱腰受正弯矩；埋深越大管片衬砌所受的最大正弯矩和最大负弯矩均增大。根据图9中的弯矩分布结果，得到围岩蠕变过程中管片衬砌最大正弯矩和最大负弯矩随埋深的变化情况如表4所示。

由表4可知，隧道埋深越大，管片衬砌的正、负弯矩也越大围岩蠕变过程中管片衬砌正、负弯矩极值的变化也越明显，结构受围岩蠕变作用的影响越大。

同上，根据数值计算结果得到围岩蠕变0、5、50、100 a时不同埋深隧道管片衬砌的轴力分布如图10所示。由图10可知，管片衬砌拱腰处轴力最大，拱顶和拱底处轴力较小。随埋深增大，管片衬砌轴力图呈向外扩展的趋势，其轴力值越大。考虑围岩蠕变效应后，不同埋深下轴力的分布特征和施工完成后(t=0 a)的分布特征相同。

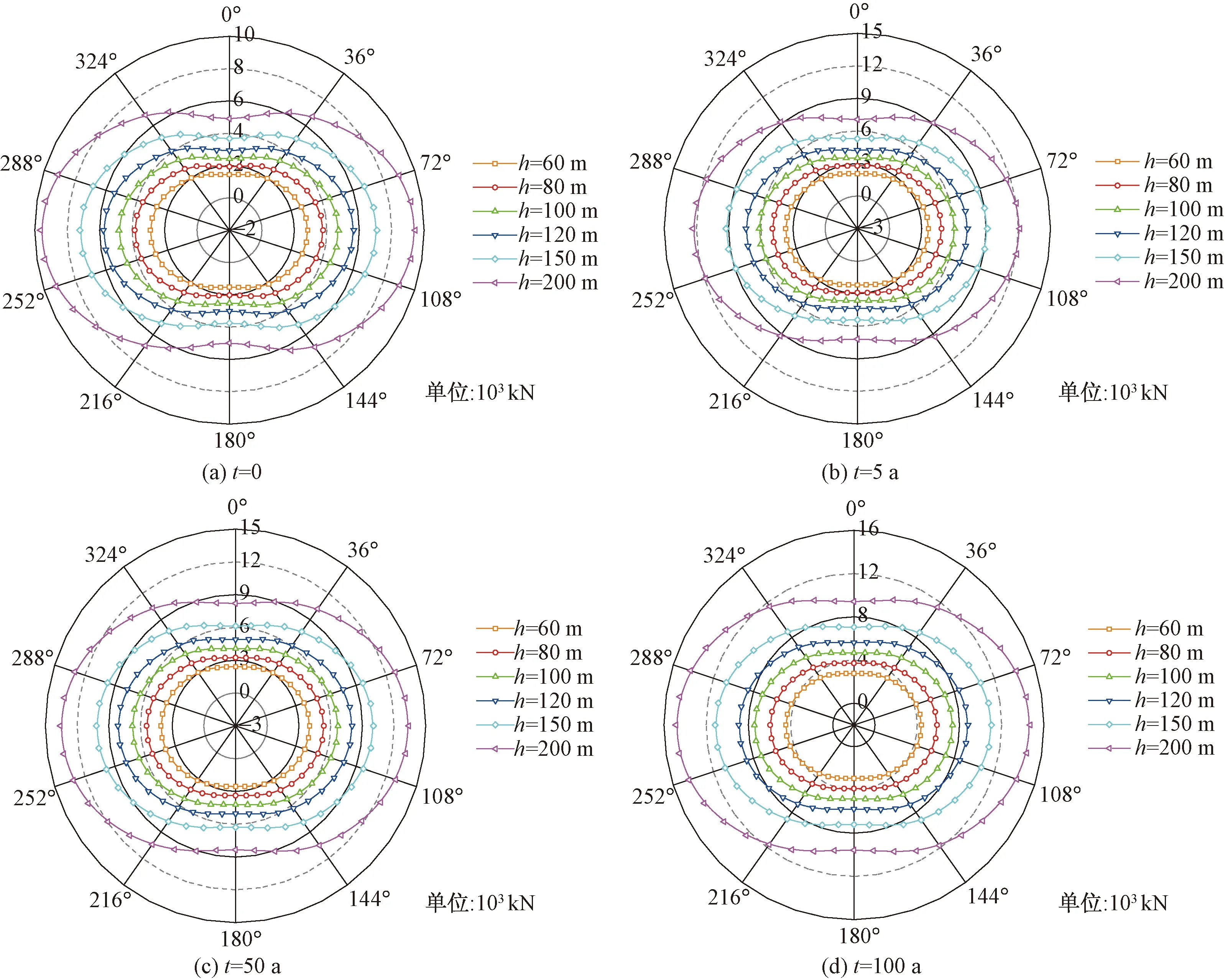
图10 不同埋深下管片轴力分布Fig.10 Axial force distribution of segments under different buried depths

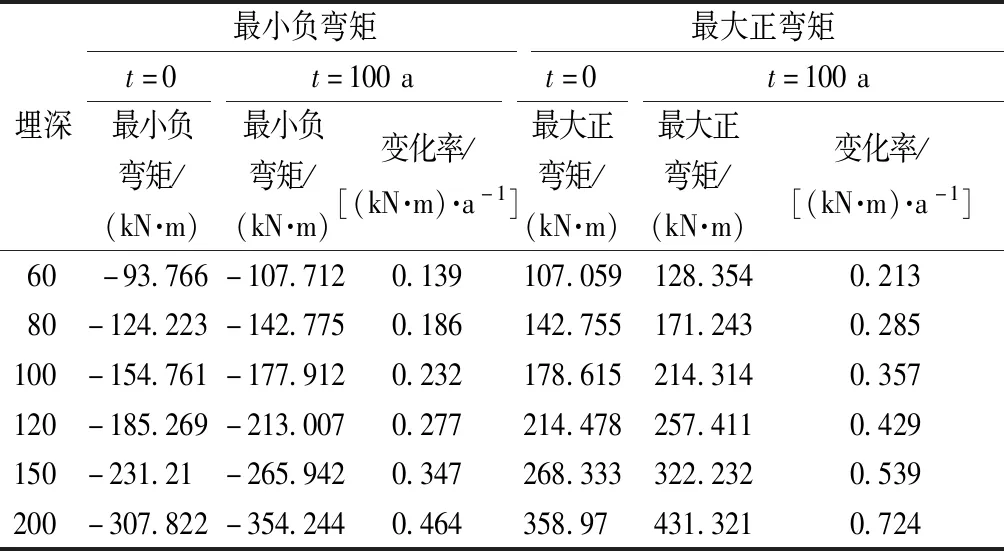
表4 蠕变过程中不同埋深工况下管片衬砌弯矩变化情况Table 4 Variation of bending moment of segment lining under different buried depth conditions during creep process

为了更加直观的研究隧道埋深对管片衬砌轴力影响，根据计算结果得到围岩蠕变过程中管片衬砌轴力极值的变化情况如表5所示。

结合表5中围岩蠕变过程中管片衬砌轴力极值的变化数据，可知在围岩衰减蠕变阶段管片衬砌的轴力变化较大，而在稳定蠕变阶段轴力缓慢变化；管片衬砌的最大轴力值随隧道埋深的增加而逐渐增大，且埋深越大轴力的变化率越大。

3.3 管片衬砌接触压力分析

利用管片衬砌和填充层之间的接触压力来分析围岩对管片衬砌的荷载作用，得到围岩蠕变过程中不同隧道埋深下管片衬砌拱顶和拱腰处的接触压力变化曲线如图11所示。由图11可知，围岩蠕变过程中不同埋深下管片衬砌外侧接触压力的变化规律与变形及内力的发展规律相同存在两个变化阶段。

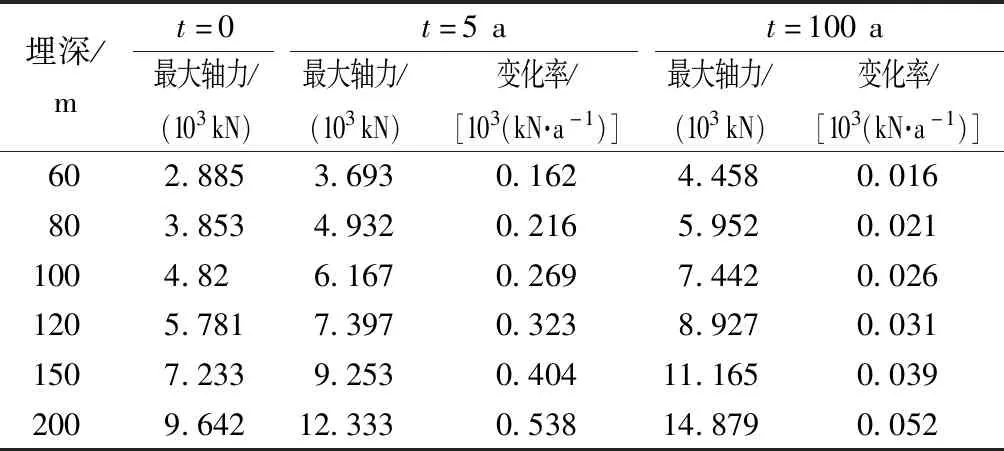
表5 不同埋深下管片衬砌轴力极值变化情况Table 5 Variations of axial force extreme values of segment lining under different buried depths

图11 不同埋深下洞周接触压力变化曲线Fig.11 Curve of contact pressure around the hole at different depths

根据该图的数据可知，随隧道埋深的增加，管片衬砌外侧接触压力逐渐增大，结构受地层围岩压力的作用越显著；围岩蠕变效应引起管片衬砌受荷作用增强，以拱顶处接触压力为例，在围岩蠕变100 a的时间里，60、80、100、120、150、200 m埋深隧道接触压力分别增加了174.567、234.556、294.342、354.059、443.447、592.006 kPa，说明隧道埋深越大，相同时间内管片衬砌接触压力的变化率更大，结构受荷受围岩蠕变的影响更显著。

4 结论

建立考虑盾构隧道施工全过程的数值分析模型，分析了围岩蠕变作用下的大埋深盾构隧道管片结构受荷特性，并从软岩隧道赋存应力场环境方面研究了围岩蠕变作用下隧道埋深对管片结构变形、内力和接触压力的影响。主要研究结论如下。

(1)开挖初期，隧道顶部围岩沉降，底部发生隆起，在考虑围岩的蠕变效应后，管片衬砌整体发生沿竖向向下的变形。随隧道埋深的增大，管片衬砌整体变形越发显著，围岩衰减蠕变阶段的拱顶竖向位移变化率远大于稳定蠕变阶段。

(2)随隧道埋深的增大，弯矩与轴力、接触压力均逐渐增大，在蠕变过程中管片衬砌受荷特征受岩体蠕变的影响也越大。在岩体未发生加速蠕变的情况下，围岩蠕变过程中管片衬砌的内力和接触压力的变化规律基本相同，有衰减蠕变和稳定蠕变两个阶段。