初中几何最值问题解法探究
成政荣

[摘 要] 数学教学已经面临着核心素养培育的需要,在几何最值问题的教学中如何兼顾学生的解题能力与核心素养,值得思考. 基于核心素养培育的需要,对初中几何最值问题解法的探究,主要分两步进行:第一步是给学生提供一些基本的最值问题;第二步是让学生进行总结. 总结的目的在于分类,以及分类基础上的方法总结. 初中几何最值问题的方法探究,一定要面向学生,面向学生的思维,这有利于核心素养强调的关键能力的落地.
[关键词] 初中几何;最值问题;解法探究
初中几何知识体系中,最值问题是一个重要的知识领域,其不仅与几何知识有关,更与数学思维有关,其既在教材上明确出现,同时又是中考的重要内容. 因此,无论是教师还是学生,对几何最值问题常常都是高度关注的. 从学生的角度来看,由于最值问题常常不知道“最”在哪里,因而学生在解题的时候,常常不像其他类型的题目那样心里有数,也因而客观上造成了学生解题时的心理紧张、无序等情形. 在解决这一问题的过程中,有数学教师尝试从方法总结的角度去寻求一类解法,这从应试效果角度来看有一定的作用,但学生总感觉自己学到的是一技之法,而不是对几何最值问题的完整认知. 今天的数学教学已经面临着核心素养培育的需要,在几何最值问题的教学中如何兼顾学生的解题能力与核心素养,成为笔者重点思考的问题. 下面就针对几何最值问题解法的探究,谈谈笔者的一些浅显观点.
初中几何最值问题概述
总体而言,初中几何最值问题因为能够综合地考查包括二次函数以及轴对称、一次函数、特殊三角形、相似三角形、特殊四边形、圆等重要知识,具有较强的灵活性、创新性和挑战性,故一直备受全国各地中考命题者的青睐. 但是命题者在享受出题成功的同时,往往较少考虑到学生会经过什么样的思维过程,才能达到问题解决、素养提升的效果,而站在核心素养培育的背景之下,对初中几何最值问题的进一步阐述,显然是非常必要的.
如上所说,几何最值问题考查的知识点涵盖如上那些方面,有同行从知识分类的角度去实现解题方法的归类,笔者以为是值得商榷的. 因为不同的知识点中,最值问题解决的思路未必相同,而不同的知识点中,最值问题的解题思路却有可能相近,因此从方法角度去对最值问题进行分类更加可行. 但是这里又存在一个挑战,那就是对于初中学生而言,数学方法、解题方法的形成与归类原本就不容易,其归类结果有可能班上只有三分之一左右的学生能够明白,这就给面向整体教学带来了难度.
在这样的背景之下,笔者在教学中当遇到几何最值问题时,在很长的一段时间里,都不给学生进行知识或者方法上的分类,而只是强调一道题目的提供与解法的形成. 这从解题心理的角度来看,其实是比较合适的,原因就在于几何最值问题对于学生而言,其实是一个经验非常缺乏的知识点,而经验缺乏就意味着需要积累,遇到一题就分析一题,解决一题就记住一题,这就是一个经验积累的过程,所积累的经验不仅包括知识点上的认识,也包括解题方法上的积累. 等到积累到一定的程度,那学生就会对几何最值问题产生一定的直觉,这种直觉是进一步提升的基础.
结合该问题在中考试卷上的体现,通过研究也可以发现,几何最值问题近年来确实颇受各地中考命题者所青睐,而且向着多形式的题型发展,并有拓宽和加深的趋势. 这类问题涉及的知识面广,综合性强,要求解题者具有较强的数学转化能力和创新意识. 这种数学转化能力和创新意识的培养,是上述经验积累到一定程度之后的必然之举.
初中几何最值问题解法
基于以上分析,基于核心素养培育的需要,对初中几何最值问题解法的探究,主要分两步进行:
第一步是给学生提供一些基本的最值问题——这里所说的基本,其判断依据是学生能够在解题之后,形成一定的方法认知. 这些基本题当中,简单如将军饮马问题,学生一旦成功解决就能够意识到轴对称知识在其中所发挥的关键作用;而略微复杂一点的则来自各地的中考题.
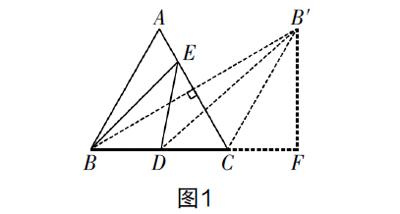
例1 在边长为2的等边三角形ABC中,点D是BC边的中点,点E是AC边上的一点(如图1),则BE+DE的最小值是______.
這道题目的解决关键在于作出B点关于直线AC的对称点. 所以从承上启下的角度来看,这道题目既是对将军饮马问题的升华,同时又强化了学生对轴对称知识在解决最值问题中的认识,实际上也就是强调了学生的方法认知.
大量事实表明,通过这一步的努力,可以帮学生形成较为丰富的解决几何最值问题的经验,即使是中等偏下的学生,也能够在成功解决问题的过程中获得方法上的认知,这一认知将为后面的分类以及方法提炼奠定基础.
第二步是让学生进行总结. 总结的目的在于分类,以及分类基础上的方法总结.
基于循序渐进的原则,对学生进行最值问题的训练,可以由“静”向“动”,譬如给学生呈现这样的例题:
例2 如图2,已知四边形ABCD中,∠A=90°,AB=3 ,AD=3,且点M,N分别为线段BC,AB上的动点(包括端点,但M与B不重合),点E和F分别是DM,MN的中点,EF的长度有无最大值或最小值?其结果是多少?
这一题目的难度,在于最值是由动点引起的,而且要判断最值是最大值,还是最小值. 难度的提升意味着学生的思维有了更大的挑战,同时也意味着思维有了更大的空间. 借助于辅助线,如连接图中的DN等,可以完成问题的求解. 而在方法的总结与反思中,需要学生认识到构建△MND,并借助于三角形的中位线定理,从而将求EF的最值转化为求DN的最值,然后去判断其是最大值还是最小值.
通过以上分析可以看出,在初中几何最值问题中,不管题目怎样变化,最值问题最终涉及的就是这样一些知识点:垂线段最短、两点之间线段最短、动点与定点最远(近)时距离最大(小)、动点与定直线最远(近)时距离最大(小)、一次函数、二次函数在某个范围内具有最大(小)值等. 基于这种知识分类走向方法分类,则可以发现几何最值问题常见的有两种:两点之间线段最短和直线外一点与直线上各点的连线中,垂线段最短,这是我们解决几何最值问题的出发点和归宿. 而最终总结出的方法则是:直接解决法(对于基础的最值问题,如将军饮马问题),转换法(如上述例2),数形结合法(通常与二次函数相关)……
特别需要指出的是,这些方法一定要经由上述两个步骤,让学生在体验的过程中不断地去总结和反思,只有当方法属于学生时,学生才会在遇到新题目的情况之下,有意识地调用自己所总结出的方法去主动解题. 如果不尊重学生在方法总结中的自主性,那无论教师多么努力,都不能保证学生在遇到新题目时能够得心应手.
面向学生思维实施教学
说白了,强调学生在解决几何最值问题过程中的方法自主总结,其实是强调学生在解决此类问题中的思维培养. 如同本文一开头所说的那样,几何最值问题与其他类型的习题并不相同,除了一些最基本的最值问题可以直觉性地形成反应之外,绝大部分题目都需要学生均有一定的思考,才能发现问题解决的方向. 作为教师,常常会为学生在解题无序时的着急而施以援手,但这种帮忙并不利于培养学生的思维. 因此在实际教学中,笔者还是倾向于让学生去自主探究,自己总结最值问题的解法.
根据笔者的经验,学生在总结的过程中,可能会有一个比较肤浅的过程. 学生总结的时候,大多只会想到“两点之间线段最短”“点到直线的距离垂线段最短”及“平面内一点与圆上各点连线中,到过该点和圆心的直线与圆的近交点距离最短、远交点距离最长”等,这些结论实际上是针对具体题目总结出来的,不具有一定的概括性,但是教师这个时候必须冷静,不能急于求成而去拔苗助长,最好的做法应当是给他们更多的题目——这些题目教师必须精选,主要的目的是丰富他们原有的认识. 可以肯定地讲,当学生对一道题目进行了总结之后,这道题目在学生大脑中的印象一般是深刻的,此时教师基于变式教学的思路,给学生提供一些变式题目,就可以丰富学生的认识,从而让他们总结出求线段或线段和、差的最值问题,及其相关的思路. 事实上,学生在这样的过程中,经常会有新的发现,比如有些题目看起来与函数无关,但是如果构造出了二次函数,就可以利用函数性质求最值. 这就是一种了不起的方法总结与发现,学生掌握的是几何最值问题的解决方法,培养的是自身的思维.
总体而言,初中几何最值问题的方法探究,一定要面向学生,面向学生的思维,不追求学生记住方法的名称,而追求学生在遇到不同类型的最值问题时,都能够有所感悟,是这一内容的教学的最佳思路,有利于核心素养强调的关键能力的落地.

