不同攻角下绕平头回转体初生空化流动特性研究

杨龙， 胡常莉， 罗倩

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

0 引言

航行体在水下高速航行时会在航行体头部附近形成低压区，当该压力低于水的当地饱和蒸汽压时，航行体周围就会产生空化现象。空化现象会影响航行体在水下运动的受力特性及运行的稳定性[1]。随着空化数的降低，空化的发展程度可以分为初生空化、片状空化、云状空化和超空化[2]。初生空化是空化发展的最初阶段，初生空化的研究涉及到空化的形成机理及生成条件，对后续空化发展以及抑制空化等研究起着重要作用。在附着型流动中，近壁面流动状态对初生空化具有十分重要的影响[3]，因此研究不同来流条件下的初生空化特性，对于附着型初生空化流动的研究是十分有意义的。

过去几十年里，人们对附着型初生空化流动进行了广泛研究。Lmdgren等[4]和Johnsson[5]对绕回转体初生空化流动进行了大量实验研究，观察到两种不同的初生空化形态，分别为游离态空泡团和“指状”附着空穴，他们认为产生不同空泡形态的原因是绕流运动是否产生了边界层分离。文献[6-7]采用全息摄影技术观测了绕回转体的初生空化流动，发现初生空化发生在流动分离区域，随后采用纹影法观察了绕不同头体的空化流动，总结出一套可以预测光滑体空化分离位置的半经验方法。随着技术的发展，高速摄像系统、粒子图像测速(PIV)系统、激光多普勒测速(LDV)系统、微型传感器等先进实验技术开始广泛应用于空化实验[8]。Wang等[2]利用高速摄像系统和LDV技术研究了二维水翼的初生空化及其他空化阶段，发现二维水翼表面空化初生时会产生一对发夹状空泡团，通过流场分析发现存在明显的发夹状涡对。Huang等[9]分别总结了绕Clark-y水翼和Tulin水翼发生初生空化时的空化数及来流攻角条件。Hu等[10]和胡常莉等[11]利用高速摄像系统和PIV技术研究了平头回转体和锥头回转体的初生空化，发现绕平头回转体和锥头回转体的初生空化均产生在肩部分离涡区域内且呈游离型发夹状，其中平头回转体的空化初生位置距离肩部及回转体壁面均较远。Wakana等[12-13]利用高速摄像系统对二维缩放喷管喉部的初生片状空化进行观察，分别研究了液体中溶解气体的量、气核分布密度和液体的流动速度对初生片状空化的影响，发现气核数量密度是影响初生片状空化的主要因素。Karuna等[14]采用高速摄像系统和PIV技术观察了后台阶剪切层内的初生空化，研究了流场结构对初生空化的影响。关于数值研究，黄彪等[15]采用一种基于空间尺度修正的滤波器模型(FBM)对绕不同头型回转体初生空化流动特性进行数值计算，该湍流模型可以准确捕捉到初生空化的流场结构，模拟得到的空穴形态与实验基本吻合。另外，黄彪等[16]还对空化流动计算中的空化模型进行对比，总结了KUBOTA、SINGHAL、KUNZ和界面动态模型(IDM)等气液相间传输模型对模拟空穴形态及演变过程的影响。Wienken等[17]采用大涡模拟(LES)方法对绕方柱体初生空化流动进行了数值研究，得到的数值结果与实验结果基本吻合。Phoevos等[18]采用不同湍流模型对柴油机喷管射流初生空化进行数值计算，结果发现雷诺时均和雷诺应力湍流模型无法预测出初生空化，而LES方法可以较好地模拟出空化的初生和发展过程。Zhang等[19]发展了一种可以预测空化核子生长迁移的动态模型，预测得到的初生空化数与实验结果对比较为一致。

本文在前人的研究基础上，基于均质两相流模型并采用LES湍流模型和Zwart空化模型，对不同来流攻角条件下绕平头回转体的初生空化流动特性进行数值研究。重点讨论不同攻角条件下初生空化分布、形态及发展规律的异同，并尝试结合流场变化，进一步分析近壁面流动结构对附着型初生空化的影响规律。

1 数值方法

1.1 控制方程和LES湍流模型

采用均质两相流模型，气体与液体两相混合物的连续性方程和动量方程如下：

(1)

(2)

式中：ui、uj表示流体速度在i轴、j轴方向的分量；p为混合流体的压力；流体黏度μ和混合流体密度ρm的定义为

μ=αvμv+(1-αv)μl，

(3)

ρm=αvρv+(1-αv)ρl，

(4)

αv为混合流体气相体积分数，μv与μl分别为混合流体汽相黏性系数和液相黏性系数，ρv与ρl分别为混合流体汽相密度与液相密度。

湍流模型采用LES方法对绕平头回转体初生 空化进行数值计算，LES方法将湍流流场中的大尺寸漩涡和小尺寸漩涡分开处理，其中大尺寸漩涡通过N-S方程直接求解，小尺寸漩涡通过亚格子模型建立与大尺寸漩涡的关系进行模拟。通过滤波函数对(1)式和(2)式过滤，得到LES方程如下：

(5)

(6)

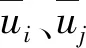
(7)

亚格子张力需要通过建模求得，目前广泛应用的涡黏性模型方程为

(8)

(9)

(10)

Ls为网格的混合长度，Ls=min (kd,CsV1/3)，k为von Karman常数，d为第1层网格离最近壁面的距离，Cs=0.5为WALE常数，V为计算单元的体积，

(11)

(12)

1.2 空化模型

空化流动计算中，选用Zwart空化模型封闭控制方程[20]，空化源项控制方程如下：

(13)

(14)

(15)

1.3 计算域设置及网格划分

计算域及边界条件设置如图1所示，回转体直径D=0.02 m、长L=0.12 m. 计算时采用与实验[21]相同的几何模型和流动条件。采用速度入口，流速u∞=8.8 m/s，对应的雷诺数Re=1.7×105；出口设置为压力出口，通过调节出口压力改变空化数。本文中空化数σ=1.2，回转体表面采用绝热、无滑移固壁条件，流动区域上下及左右边界均设置为自由滑移壁面条件。

图1 计算域、边界条件设置及近壁面网格加密示意图Fig.1 Computational domain， boundary conditions and near-wall grid of blunt body

计算域采用六面体结构化网格，并对回转体表面及近壁面区域进行网格加密处理(见图1)。另外，采用4套不同加密程度的网格对绕平头回转体无空化的单相流动进行数值计算，讨论LES方法对网格尺度的敏感性，如图2所示。从图2中可以看出，采用不同加密程度的网格计算得到的分离涡尺度各不相同，随着网格数的增加，分离涡的尺度有所减小。

图2 不同网格时平头回转体纵切面上的时均流线图及网格示意图Fig.2 Time-averaged streamline patterns and grids on the longitudinal section of blunt body with different grids

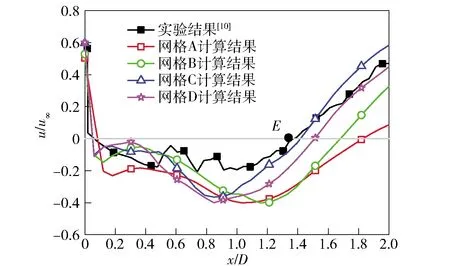
图3 采用不同网格计算得到的平头回转体表面时均速度分布与实验结果对比Fig.3 Comparison of time-averaged velocity distributions of blunt body calculated by different grids and experi-mental results

为了进一步讨论网格数对计算结果的影响，提取了回转体表面的时均速度u分布曲线，并与实验结果[10]进行对比，如图3所示。图3中E点表示由实验得到的流动再附着点。从图3中可以看出：采用不同网格计算得到的时均速度u的变化趋势均与实验曲线基本相似，在x/D=0处，时均速度u迅速下降由正值变为负值，之后在流动分离区域保持负值且变化较平缓；当靠近流动再附着点时，时均速度u又逐渐增大由负值变为正值。与其他网格相比，采用网格C计算得到的流动再附着点位置与实验值更加接近。

图4 采用不同网格计算得到的时均阻力系数Fig.4 Time-averaged drag coefficient calculated by different grids

2 结果与讨论

2.1 初生空穴的形成及发展特性

表1给出了绕平头回转体的初生空化形态随时间的演变情况。从表1中可以看出：数值计算与实验拍摄得到的初生空穴的发展特性基本一致：t0时刻，在回转体肩部形成发夹涡对状初生空穴；t0至t0+0.36T，涡对状空穴逐渐融合、长大；之后空穴逐渐缩小直至溃灭。初生空穴在随时间演变的同时，会随主流向下游运动。

表2给出了典型时刻下的空穴形态图和纵切面上的近壁面涡量分布情况。与文献[10]的实验结果对比可知，数值计算可以较好地模拟初生空穴形态及其在回转体肩部的分布位置。另外，数值计算得到的涡量分布特点与实验结果吻合较好，即高涡量区域分别呈带状和零散状分布，且分别对应于分离涡剪切层区域和初生空穴区域。

图5给出了不同攻角条件下初生空化在典型时刻的形态图。图5(a)和图5(b)分别是0°攻角条件下，实验观测与数值计算得到的绕平头回转体初生空穴的典型形态图。由图5(a)和图5(b)可以看出，数值计算得到的初生空穴形态呈不规则的团泡状并且不对称地分布在回转体肩部区域，与实验观测结果吻合较好。图5(c)和图5(d)分别是数值计算得到的5°攻角及10°攻角条件下初生空穴的典型形态图。对比不同攻角条件下的空穴分布特点发现，有攻角条件下初生空穴的不对称分布特点更加明显。随着攻角的增大，迎流区域的初生空穴向回转体头部及壁面靠近，而背流区域的初生空穴逐渐远离回转体壁面。值得注意的是，10°攻角时在背流区域的下游近壁面处也产生了初生空穴。

表1 0°攻角条件下初生空化形态随时间的演变过程

Tab.1 Time-evolution process of cavity at 0° angle of attack

注：T为空泡从形成到溃灭的一个周期。

表2 0°攻角条件下绕平头回转体瞬时空穴形态及涡量分布

Tab.2 Instantaneous structures of incipient cavitation and the correspondingz-vorticity field at 0° angle of attack

图5 不同攻角条件下绕平头回转体初生空化的典型形态对比Fig.5 Comparison of typical instantaneous structures of incipient cavitation at different angles of attack

绕平头回转体初生空穴的发展过程具有较强的随机性，本文针对不同攻角条件统计了绕平头回转体初生空穴的形成及溃灭位置，绘制成点状图，如图6(a)和图6(b)所示，统计过程中以初生空穴的中心坐标作为统计量。从图6中可以看出，随着攻角的增大，迎流区域的初生空穴分布范围逐渐向回转体头部及壁面收缩，而背流区域的初生空穴分布范围逐渐远离回转体壁面。值得注意的是，10°攻角时，存在几组初生空穴分布在回转体背流区域下游的近壁面处。另外，随着攻角增大，迎流区域初生空穴的溃灭位置逐渐向形成位置的下方移动，背流区域初生空穴的溃灭位置逐渐向形成位置的上方移动。表明随着攻角的增大，迎流区域的初生空穴从形成到溃灭逐渐向回转体壁面靠近，背流区域的初生空穴从形成到溃灭逐渐远离回转体壁面。

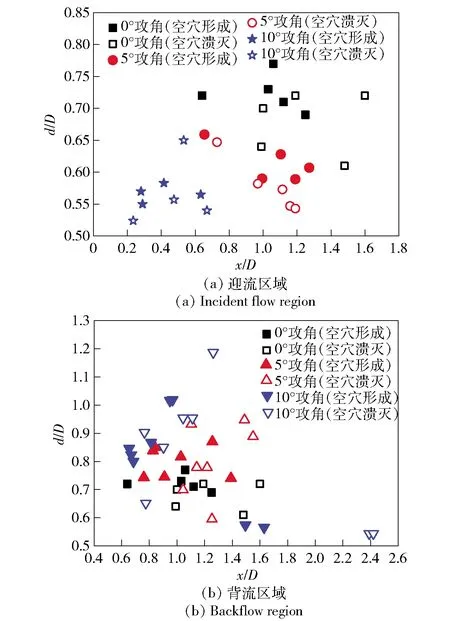
图6 不同攻角时初生空穴的形成位置及溃灭位置分布Fig.6 Formation and collapse location of incipient cavities at different angles of attack

表3给出了不同攻角条件下绕平头回转体初生空穴的分布区域统计，其中10°攻角背流区域未考虑下游近壁面处的初生空穴。由表3可知，0°攻角时，数值计算得到的初生空穴分布区域与文献[21]的实验结果基本一致。随着攻角增大，迎流区域的初生空穴在轴向及径向上的分布区域均逐渐减小且向回转体头部及壁面靠近。背流区域的初生空穴在轴向上的分布变化不明显，在径向上的分布区域逐渐扩大且远离回转体壁面。

表3 不同攻角时初生空穴的分布区域统计Tab.3 Statistics on the distribution area of incipient cavities at different angles of attack

2.2 初生空化流场分析

文献[21]指出，绕平头回转体初生空穴均发生在回转体肩部分离涡区域内。图7给出了回转体表面的时均速度u分布曲线。从图7中可以看出，随着攻角的增大，迎流面的流动分离区域尺度减小且逐渐向回转体头部推移，背流面流动分离区域的位置及尺度的变化不明显。图8给出了回转体表面的时均压力系数分布曲线。对比不同压力系数曲线发现，同一攻角条件下，迎流面上的逆压梯度明显大于背流面，促使迎流面上的反向速度大于背流面；随着攻角增大，迎流面上的高逆压梯度区域逐渐向回转体头部推移，使得迎流面上的流动分离区域向回转体头部移动。

图7 不同攻角条件下回转体表面的时均速度分布曲线Fig.7 Time-averaged velocity distribution of axisymmetric body at different angles of attack

图8 不同攻角条件下回转体表面的时均压力系数分布曲线Fig.8 Time-averaged pressure coefficient distribution of axisymmetric body at different angles of attack

图9给出了绕平头回转体近壁面的分离涡结构示意图，分离涡结构的轴向尺度由图7中的流动分离区域尺度可知，其径向尺度如图9中标注所示。从图9中可以看出，随着攻角增大，迎流面的分离涡结构尺度逐渐减小，并且向回转体头部及壁面靠近，而背流面分离涡结构在径向上的尺度逐渐增大。另外，观察图9(c)发现，10°攻角时，在背流面的分离再附着点附近产生了二次分离涡结构。结合初生空穴的分布特点发现，初生空穴的分布区域与回转体表面的分离涡结构息息相关：随着攻角增大，迎流面初生空穴的分布区域逐渐减小且向回转体头部及壁面靠近，而背流区域初生空穴在轴向上的分布变化不明显，在径向上的分布范围逐渐扩大且远离回转体壁面；大攻角条件下，背流面的流动分离再附着点附近产生了空穴。由此可见，受到来流攻角的影响，分离涡结构发生变化，促使初生空穴的分布特性产生了相应的变化。

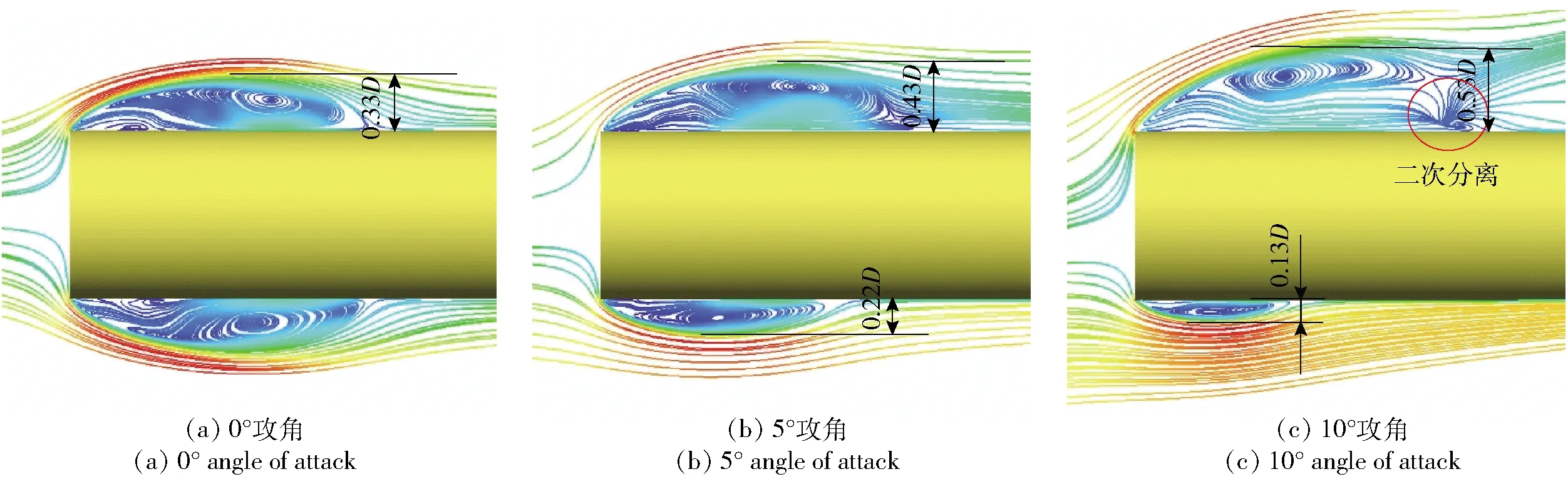
图9 不同攻角条件下回转体纵截面上的时均速度流线图Fig.9 Time-averaged streamline on the longitudinal section of axisymmetric body at different angles of attack

图10 不同攻角条件下回转体背流面的空泡形态及瞬时速度矢量图(右为放大图)Fig.10 Cavitation shapes and instantaneous velocity vector on the backflow surface of axisymmetric body at different angles of attack (right: enlarged view)

图10给出了不同攻角条件下回转体背流面典型时刻的空泡形态图及速度矢量图。从图10中可以看出，不同攻角条件下，初生空穴均呈团泡状游离态分布在回转体肩部分离涡区域。与0°和5°攻角对比发现，10°攻角时，在背流面下游区域的近壁面处产生了初生空穴，结合速度矢量图可以看出，此时在距离回转体头部约1.9D处存在明显的近壁面漩涡结构。

图11给出了对应时刻回转体表面的瞬时速度u的变化曲线。对比不同攻角条件下的速度曲线可知：0°攻角时，在x=1.9D处的速度为正值(如方框所示)，表明没有形成反向射流；5°攻角及10°攻角时，该处速度为负值，表明存在明显的反向射流。相比较而言，10°攻角条件下反向射流的速度明显较大，较强的反向射流与主流相互作用促使发生二次分离，并在当地形成了漩涡结构。

3 结论

本文采用LES方法模拟了不同来流攻角条件下绕平头回转体的初生空化流动，并与实验结果进行了对比。得到以下主要结论：

1) LES方法可以较好地模拟绕平头回转体的初生空化流动。数值计算得到涡对状初生空穴及空穴融合、长大、断裂、溃灭的过程与实验结果基本一致；数值模拟预测的空穴在回转体肩部的分布位置及近壁面的涡量分布均与实验结果十分吻合。

图11 不同攻角条件下回转体背流面的瞬时速度分布曲线Fig.11 Instantaneous velocities of backflow surface of axisymmetric body at different angles of attack

2)各攻角条件下，初生空穴均呈不规则团泡状并且不对称地分布在回转体肩部的分离涡区域内。随着攻角增大，不对称分布特性更加明显：迎流面的初生空穴分布区域逐渐缩小且向回转体头部及壁面靠近，背流面的初生空穴分布区域逐渐扩大且远离回转体壁面。

3)初生空穴的分布规律与分离涡结构紧密相关。随着攻角的增大，迎流面分离涡尺度逐渐减小并向回转体头部及壁面移动，而背流面分离涡尺度逐渐增大。大攻角条件下，在背流面的分离再附着点的附近存在较强的近壁面反向射流，反向射流与来流作用产生了二次分离，促使该区域发生初生空化。