高维参数不确定爆轰的不确定度量化
梁霄, 陈江涛, 王瑞利
(1.山东科技大学 数学与系统科学学院, 山东 青岛 266590; 2.中国空气动力研究与发展中心, 四川 绵阳 621000;3.北京应用物理与计算数学研究所, 北京 100094)
0 引言
物理试验、理论推导、数值模拟是目前研究爆轰的3类主要方法[1-6]。比较而言,数值模拟具有成本低、安全无风险、过程可控等优点。伴随计算机存储和运算能力的提高,高精度、高保真格式的算法逐步用于求解爆轰模型,进一步提高了运算精度[7]。然而爆轰建模与模拟(M&S)中以下两个问题仍然没有很好地解决: 1)M&S中设置的初边值条件、模型形式、模型参数是否值得信赖?2)爆轰过程的复杂性和人类认知的局限性,导致爆轰流体力学模型中不仅含有大量假设、简化和近似,而且含有众多类型的不确定性因素[1-7],这些不确定因素对系统输出结果的影响需要评估。
验证、确认和不确定度量化(V&V&UQ)技术可以用以解决上述疑问。不确定度量化(UQ)是一门蓬勃发展的学科。目前,美国Sandia National Laboratory、Los Alamos National Laboratory、Lawrence Livermore National Laboratory均成立了相关UQ研发部门,致力于暂停核试验后维护核武器库的日常运转、保证武器的可靠性,开发UQ软件Dakota和UQknit. 2013年以来,斯坦福大学、麻省理工学院、南加州大学等部分高校成立了专门的UQ团队。在学术界,2016年美国机械工程师(ASME)协会创刊Journal of Verification, Validation and Uncertainty Quantification,注重UQ技术在工程领域的应用。同时UQ技术在航空航天、军用和民用核技术等领域应用广泛[8-10]。
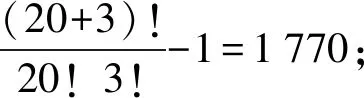
1947年Metchell等[25]最早论述了绕爆试验中的拐角处的漩涡和死区。此后愈来愈多学者从事这一领域的研究[26]。1976年Mader等[27]利用HOM状态方程和Forest Fire反应率模型成功地模拟出基于三氨基三硝基苯(TATB)炸药X-0219在拐角处的绕爆现象,为爆轰研究提供了经济快捷的途径。绕爆现象的模拟严重依赖于状态方程和反应率方程的选取,并且对参数和位置敏感,如何量化和刻画参数与物理量的波动对系统输出结果的影响,关系到能否合理评估数值模拟方法的可信度,是一个极具挑战性的课题。
综上所述,多不确定参数绕爆试验的UQ研究尚未见报导。本文以绕爆试验为基准试验,提出一种改进的基于回归方程的多项式混沌方法,用以处理不确定爆轰系统的UQ问题。该方法能缓解维数灾难问题,具有计算可行性。所得结果能预测绕爆动力行为,为研发高可信度爆轰程序提供依据。
1 爆轰物理数学模型
1.1 爆轰控制方程
爆轰过程所使用的数学物理模型为基于守恒原理的二维Euler方程组,在拉格朗日坐标系下表征[2,6,11]为
(1)
(2)
(3)
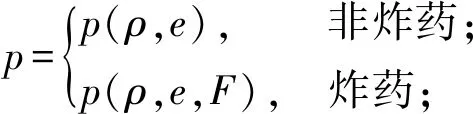
(4)
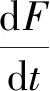
(5)
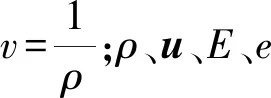
1.2 反应率唯象模型
采用依赖于网格的Wilkins反应率模型研究绕爆[2,6,11], 其形式为
F=[max (FC-J,Ft)]nb,
(6)

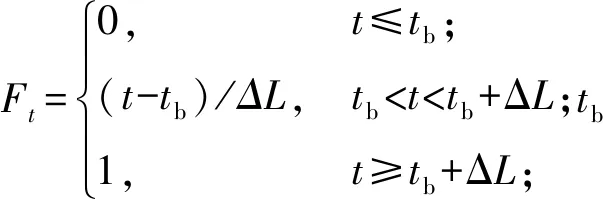
1.3 状态方程
爆炸产物采用JWL状态方程[6,17],具体如下:
(7)
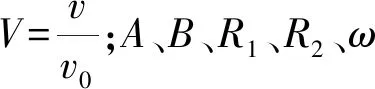
(8)
AR1exp (-R1VC-J)+BR2exp (-R2VC-J)+
(9)
(10)
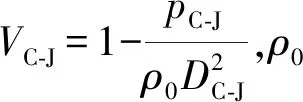
1.4 计算方法
本文的计算模型基于任意多边形非结构网格,利用拉格朗日自相容有限体积方法及Landshoff一次黏性aL、von Neumann-Richtmyer二次黏性aNR、子网格压力、人工热流等抑制非物理振荡的方法,以及多介质滑移计算推广到任意多边形非结构网格,构造了一套任意多边形非结构网格流体大变形强适应的高精度有限体积格式,并采用了网格大变形处理的邻域可变技术。
对于拉格朗日方法,重点和难点是动量方程的离散,本文使用已有限体积格式,给出动量方程的离散化。如图1所示,把节点α周围网格的中心和过节点α网格边的中点按逆时针方向连线,得到有限控制体积Ωα,称为节点α的控制体。其中节点αk为节点α的第k个邻域节点,即点α1,α2,…,αmα为与节点α共线的网格节点,mα为节点α邻域网格数;网格ik为节点α的第k个邻域网格,即点i1,i2,…,imα为邻域网格的中心点;节点βk为以节点α与节点αk为端点的线段中点,即点β1,β2,…,βmα为共线边的中点。图1中节点α的速度沿虚回路积分求解公式为
(11)
(12)

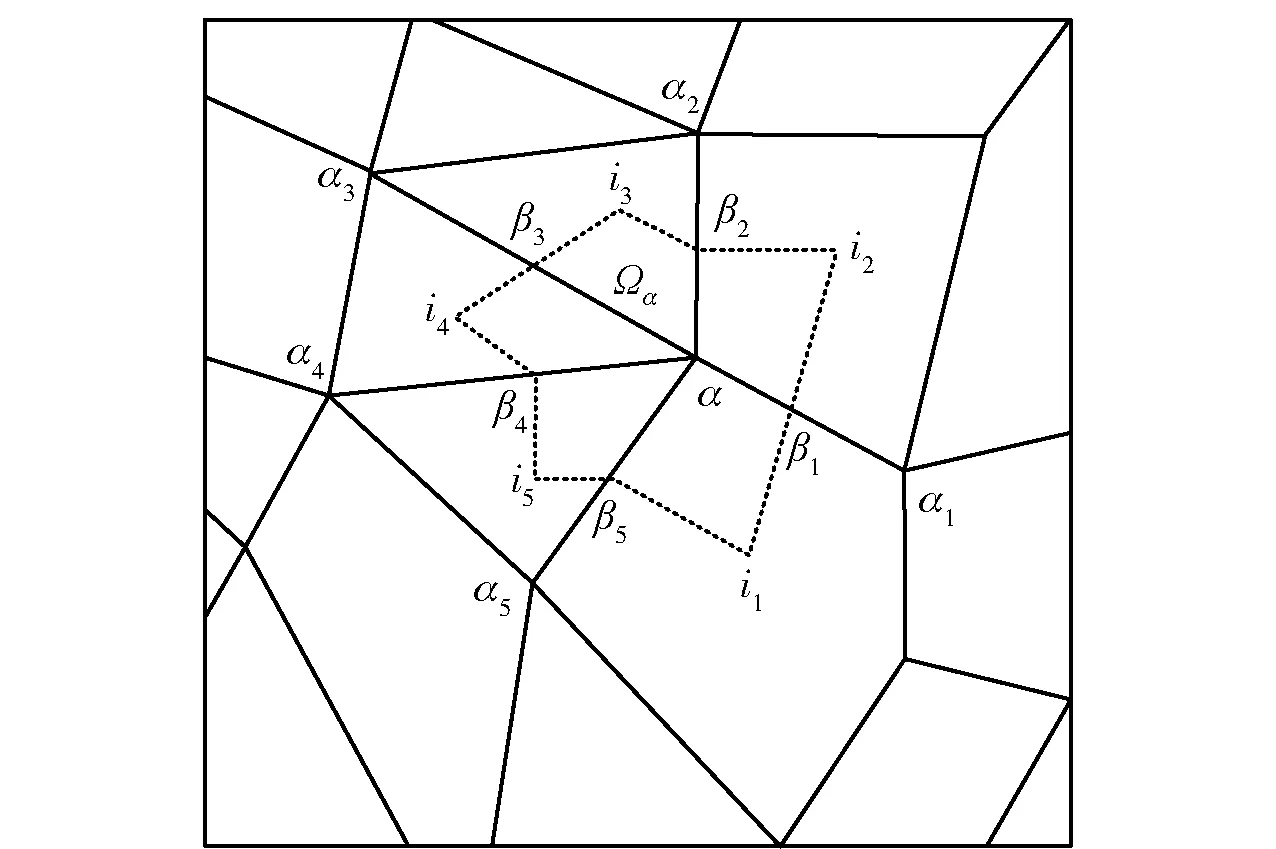
图1 动量方程控制体积ΩαFig.1 Control volume Ωα for momentum equation
1.5 确定性数值模拟
首先使用单个确定数值模拟,验证算法的有效性以及状态方程和反应率方程选取的正确性。试验装置与计算模型如图2所示。图2中,D、S为拐角附近两个拉格朗日参考点。拐角附近伴随着激波的折射、反射、漩涡、死区、振荡等非线性特征丰富,动力行为具有代表性。计算模型左边小通道高0.5 cm、长1.0 cm,右边大通道高2.0 cm、长2.0 cm;上界面是固壁,下界面是对称轴,左右界面是自由面;内部充满PBX-9404炸药;初始在左边面起爆,平面爆轰波将向右传播,从左边较小尺寸药柱传入尺寸较大的药柱中。爆轰数值模拟采用JWL 状态方程 (见1.3节)和Wilkins反应率模型(见1.2节)。炸药产物JWL状态方程参数取A=852.4,B=18.02,R1=4.6,R2=2.3,ω=0.38. Wilkins反应率中参数nb、γb分别为1.1、2.1,计算网格规模选取72 000单元。 数值模拟计算结果和试验结果如图3所示。

图2 爆轰试验装置及计算区域Fig.2 Experimental setup and computational domain of detonation
从图3中可以看出:炸药爆轰波从狭窄管道往突扩管道传播时,爆轰波从爆轰管内传播出来并且绕过拐角往突扩口外传播,拐角处将诱导出一道漩涡;当爆轰波撞击壁面后反射激波向通道中心传播时,在拐角附近产生分叉,靠近拐角部分反射激波呈凸起状。数值模拟结果与试验基本一致,确认了算法的有效性。
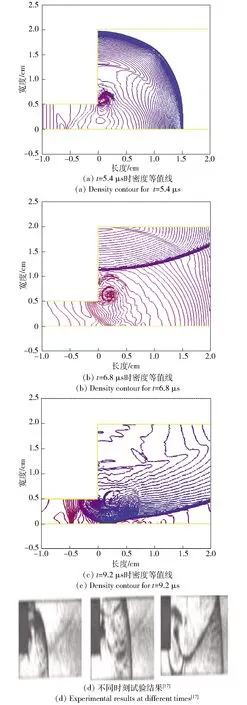
图3 绕爆试验模拟结果与试验结果对比Fig.3 Comparison between simulated and experimental results
2 UQ和NIPC
2.1 不确定度来源
爆轰过程含有大量不确定因素[6,11,14]:一是物理量固有的不确定度。例如在炸药加工过程中,孔洞和间隙会发生随机波动、晶体位错和缺陷、杂质颗粒混入等,都会导致炸药颗粒凝结不均匀,使得密度的分布呈现随机性,同时测量技术的不精确性也会导致测量结果的波动。因此,理论上应该用概率方法描述炸药初始密度。假设炸药PBX-9404的初始密度ρ服从区间[1.8 g/cm3,1.9 g/cm3]上的均匀分布,即ρ~U(1.8 g/cm3,1.9 g/cm3),U(a,b)表示区间[a,b]上的均匀分布。二是由1.1节~1.3节可知,爆轰模型中含有大量惟象参数,没有物理意义,通常依据经验确定,这类参数属于认知不确定度。假设此类参数满足均匀分布,区间大小取决于专家意见、经验和统计结果。
不确定度的具体描述如表1所示。

表1 绕爆过程中的不确定度Tab.1 Uncertainty of detonation diffraction
2.2 多项式混沌理论
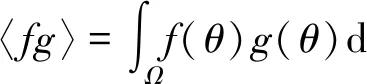
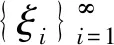
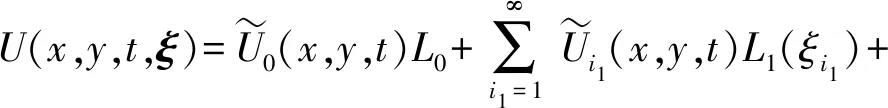
(13)
式中:Lm表示m次多元多项式,由随机变量的类型决定,对应方式见文献[18]。基于本文假设,随机变量服从均匀分布,故Lm选取m次Legendre多元多项式。
将(13)式写成更加紧凑的形式,得U(x,y,t,ξ)=

(14)

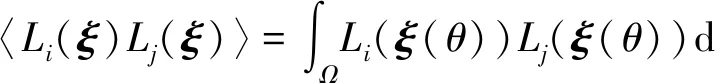
(15)
2.3 逆累积分布函数和Rosenblatt变换
由2.2节知,多项式混沌理论成立的前提是随机变量组{ξ1,ξ2,…,ξl}为1列独立同分布的均匀随机变量,然而这并不适用于本文的研究对象。由2.1节{ξ1,ξ2,…,ξl}并不是标准均匀随机变量组,由1.3节(8)式~(10)式可知,R1、R2、ω,A、B、C也不满足相互独立性。因此必须对随机变量组做适当变换,方可使用前述内容。
首先,使用逆累积分布函数变换将一般均匀分布转化成标准均匀分布。步骤如下:
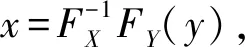
2) 使用Rosenblatt变换将{ξ1,ξ2,…,ξl}转化为服从U(0,1)的独立随机变量组。利用条件概率的概率等交换原则[28]:
FY1(y1)=FX1(x1),FY2(y2|y1)=FX2(x2|x1),⋮FYl(yl|y1,y2,…,yl-1)=FXl(xl|x1,x2,…,xl-1),
从而
(16)
则{Y1,Y2,…,Yl}是一列服从U(0,1)的独立同分布的随机向量组。
2.4 NIPC理论
本文采用NIPC计算:

(17)

(18)
式中:ξ(i)为采样点;M为采样点数;α1,α2,…,αN表示字典序N次Legendre多元多项式。将(18)式表示成更加紧凑的矩阵形式,即Gc=U.
(19)
式中:‖c‖1表示c的1-范数。使用基追踪方法[22]将(19)式转化为线性规划问题:
(20)
式中:kT=(1,…,1),k∈2N;A=[G-G];x∈2N. 通过求得(20)式的最优解x*,从而得到(19)式的最优解为c*=x*[1∶N]-x*[N+1∶2N]。本文计算中,选取d=3,M=20.
3 绕爆UQ结果
利用第2节所述方法,得到拉格朗日参考点D和S的水平方向速度、水平方向位置、压力等系统响应量的期望和置信区间,置信区间对应的置信水平为95%,具体信息如图4~图9所示。由图4~图6可以看出:在时间3.64 μs处压力和速度急剧地增加,对应爆轰波的产生。但是与理想情况不同,激波过后,拉格朗日参考点的速度和压力的期望并非单调递减,而是剧烈地振荡,且曲线的光滑性较差,但位移曲线的光滑性较好,压力和速度的峰值甚至比爆轰波处压力速度值还高。这与算法相关,对应了拐角处爆轰的动力行为,也与爆轰波的反射有一定关系。同时拉格朗日参考点的位置并非一直往前运动,在一定时刻又向后运动甚至比初始位置更加靠后,与爆轰波的折射密切相关。表明拐角处每一点的轨迹都不尽相同,与拐角处炸药复杂的动力学行为相对应。同时D、S两点并没有过多的相似之处,表明UQ结果与拉格朗日参考点的位置密切相关。
图7~图9给出了系统输出结果置信区间,即系统响应量在固定时刻的变化范围。从图7~图9中可以看出,在同一置信水平下,伴随着时间的演化,置信区间越来越宽,表明在多随机因素扰动对系统的影响伴随着时间的增长而逐渐加强,预测长时间动力行为要比瞬时行为困难得多。

图4 水平方向速度期望随时间的变化Fig.4 Expectation of x-velocity versus time

图5 水平方向位置期望随时间的变化Fig.5 Expectation of position versus time
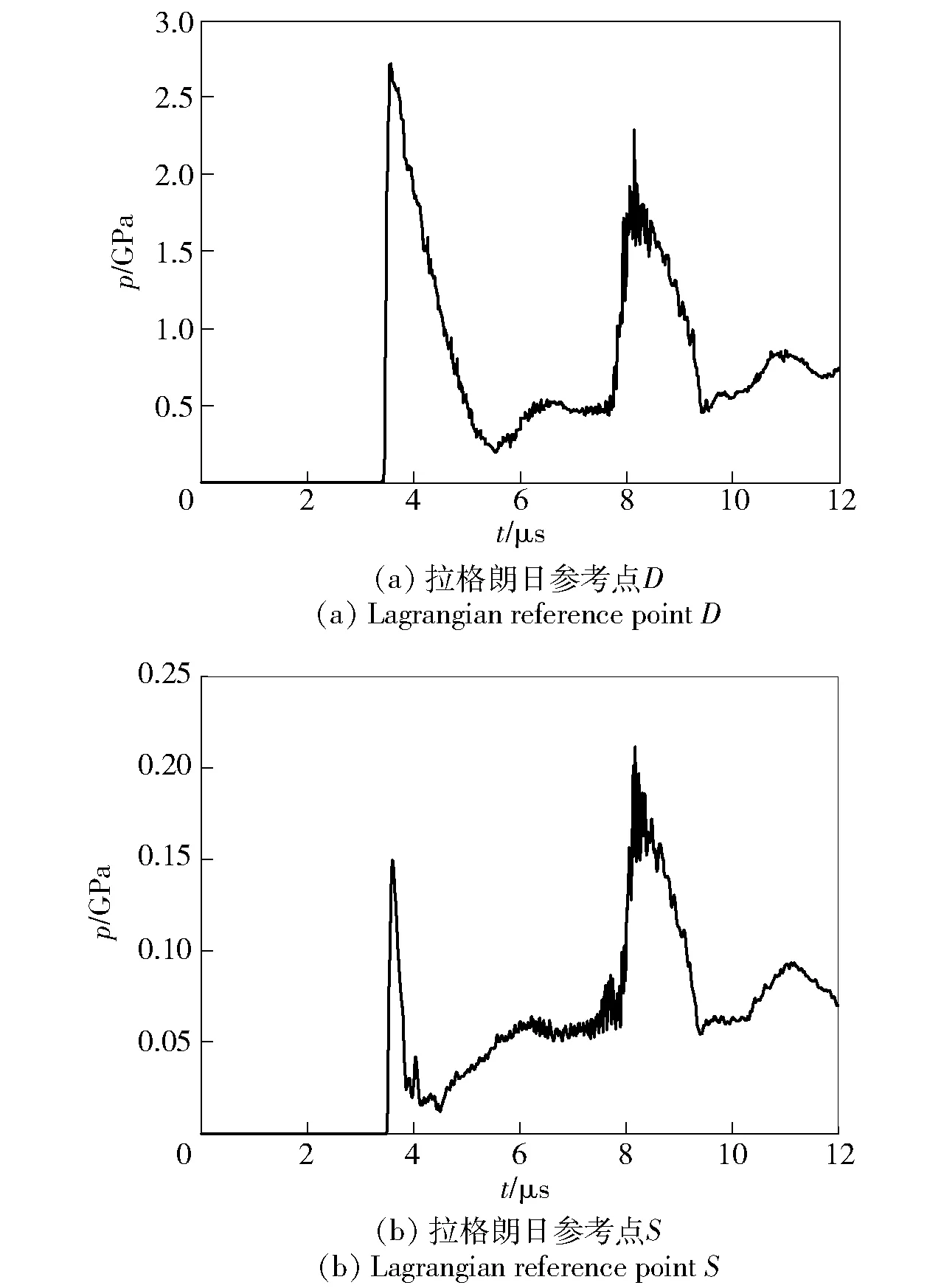
图6 压力期望随时间的变化Fig.6 Expectation of pressure versus time
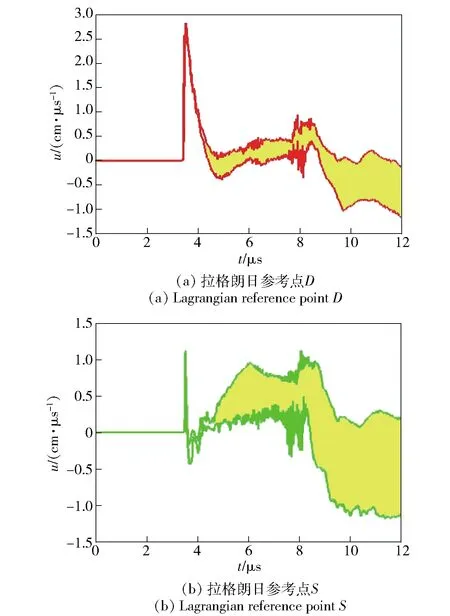
图7 水平方向速度置信区间随时间的变化Fig.7 Confidence interval of x-velocity versus time

图8 水平方向位置置信区间随时间的变化Fig.8 Confidence interval of position versus time
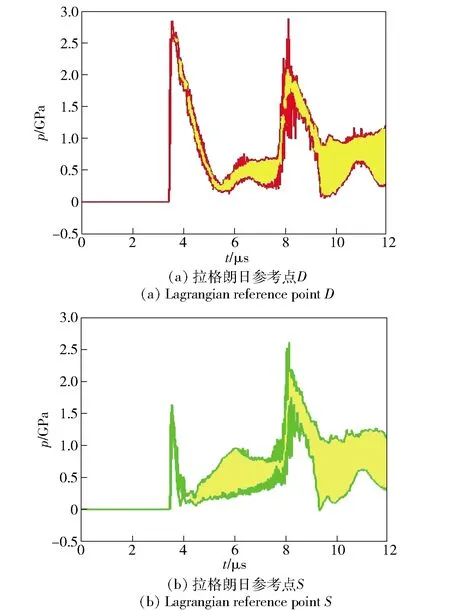
图9 压力置信区间随时间的变化Fig.9 Confidence interval of pressure versus time
4 结论
本文主要研究高维参数不确定度对系统的影响,使用均匀分布表征和量化平面拐角绕爆模型的不确定因素,并使用基于回归方法的NIPC方法评估高维不确定度对系统输出结果的影响,在一定程度上缓解了“维数灾难”问题;给出了两个拉格朗日参考点的速度分量、位置、压力的期望和置信区间,初步完成了拐角系统的UQ. 得出以下主要结论:速度和压力的期望剧烈振荡,位移的期望光滑性、平滑性较好,拉氏参考点的位置并非一直往前运动;系统输出量在置信区间内变动;绕爆模型对拐角处位置选取敏感,不易预测长期动力行为;所得结果为发展高可信度数值模拟软件打下了坚实的基础;所用UQ方法具备计算可行性,可以推广到其他爆轰问题。
下一步研究拟进一步考虑如下问题:
1)绕爆现象的数值模拟对状态方程和反应率方程的选取敏感,直接关系到拐角效应模拟的成败。下一步拟研究不同的状态方程和反应率方程对系统输出结果的影响,即模型UQ.
2)本文侧重于数值模拟结果的UQ. 然而,炸药中的随机孔洞、杂质以及几何尺寸偏差均会引起待测试验结果的波动。如何在综合考虑试验结果及数值模拟结果不确定度的条件下对比试验结果和数值模拟结果,是一个极具挑战性的课题,也是下一步研究的对象。
致谢山东科技大学公派访问学者项目的资助。

