一种新型物料装填机器人的设计与轨迹优化

郑昱， 广晨汉， 李前， 杨洋

(1.北京航空航天大学 机械工程及自动化学院, 北京 100191; 2.上海航天技术研究院 上海无线电设备研究所, 上海 201109)

0 引言

在战场物资补给、抢险救灾等工作环境中，一些必要的生产过程需要在车辆内部进行。在车辆内部狭小空间中连续输送和装填大质量物料，对工人来说是一项强体力劳动，且使用人工进行物料输送和装填不利于车辆作业的稳定性和车辆作业的经济性。

搬运机器人是一种由程序控制的工业机器人，可自动完成所在工位的物料输送任务。目前搬运机器人主要应用于机床自动送料、工件搬运和码垛搬运等自动化场合[1]。搬运机器人的构型、运动学特性和关节轨迹，是搬运机器人的重要研究内容。搬运机器人的构型主要包括串联结构和并联结构两种，基于串联结构的搬运机器人主要为4轴或6轴，适用于大工作半径场合[2]。基于并联结构的搬运机器人多基于Delta机器人研发，已广泛应用在包装车间流水线和分拣车间流水线上[3]。

运动学特性研究方面，Denavit等[4]提出了齐次变换矩阵(D-H参数)法，已逐渐成为机器人运动学建模的主要方法。Rocha等[5]使用螺旋位移法和D-H参数法，对多自由度机器人的正运动学进行了研究。高文斌等[6]使用全局指数积法获得机器人运动学模型，但该方法计算比较复杂。轨迹规划通常在关节空间或笛卡尔空间中，通过求解轨迹函数完全确定机器人所需的期望运动[7]。运动轨迹规划中常用的插值方法有B样条法[8]、NURBS曲线法[9]、高次多项式插补法[10]等。最大速度[11]、能耗最小[12]、振动幅度最小[13]、规避局部最小值[14]也是文献中使用的轨迹优化目标。

综上所述，搬运机器人已在工业生产中得到广泛应用，但缺乏在有限空间中使用的先例，相关的构型设计、工作空间分析和轨迹优化的研究成果也相对较少。因此，本文提出一种在有限空间内使用的物料装填机器人，针对某型号车辆内所需的圆柱物料搬运、装填要求和约束空间的限制条件，设计物料装填机器人，并对其构型设计、工作空间计算、轨迹优化方面的内容开展研究，以期在车辆内高效执行物料输送动作，满足车辆快速作业的要求。

1 机器人总体设计

1.1 总体技术要求

本文设计的物料装填机器人需要输送的圆柱物料为规格一致的生产原料，物料高度约1 085 mm，直径约130 mm，质量约35 kg. 圆柱物料均匀存放于车中的存储仓内，存储仓内的传动链可使圆柱物料沿固定轨迹水平移动至取料口。物料装填机器人从取料口抓取物料，推送至物料加工设备中。圆柱物料在车内的运动如图1所示。由图1可知，圆柱物料需要在空间中3个自由度上移动，且在1个自由度上转动，因此要求物料装填机器人至少具有4个自由度。

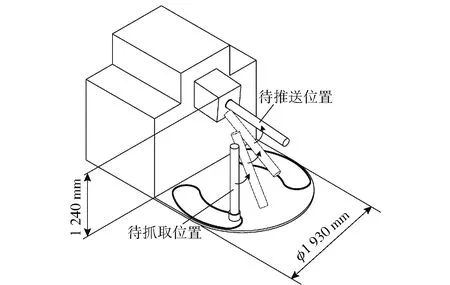
图1 圆柱物料在车内的运动Fig.1 Motion of cylindrical materials in vehicle

考虑到物料加工过程中，物料加工设备会产生后移动作，因此要求物料装填机器人不能与车辆和物料加工设备产生干涉。车内空间约束见图1，车内空间为直径1 930 mm、高1 240 mm的圆柱空间。同时，为提高生产效率，要求一次物料装填动作的用时不得超过3 s.

综上所述，可得到物料装填机器人的技术要求：

1)机器人末端具有至少4个自由度，且具备避障能力，能够避开加工设备的后移动作。

2)运动空间满足物料装填动作的需求，且具有尽可能多的操作空间。

3) 输送动作快速平稳，一次装填时间不超过3 s.

1.2 总体设计方案

基于1.1节的设计要求，提出一种RPP-RR结构的物料装填机器人，R表示转动关节，P表示平动关节。

本方案中，物料装填机器人由整体转动关节(关节1)、横移关节(关节2)、举升关节(关节3)、调姿关节(关节4)、避障关节(关节5)和末端抓持器6部分组成。其中：关节1通过转盘轴承安装在车内空间底部，可带动布置其上的所有关节转动；关节2和关节3相互垂直、组成一个平面，可对圆柱物料的平面位置进行调整；关节4用于调整圆柱物料与水平面的夹角，使其与进料口轴线共线；关节5可绕自身轴线旋转90°，从而避开物料加工设备的后移动作。

物料装填过程如下：首先解除避障状态，关节5转动90°至抓持位置，同时关节1、关节2、关节3协调运动，使末端抓持器对准圆柱物料；随后，末端抓持器抓稳物料，关节1、关节2、关节3、关节4协调运动，将物料送至进料口；末端抓持器松开物料，推送机构将物料推入加工设备；推送机构回位后，各关节回位，完成一个物流装填流程。

2 运动学建模和工作空间分析

2.1 运动学建模

为验证机器人的操作空间能否满足设计要求，需要建立机器人的运动学模型，并对其工作空间开展定量分析。

依据1.2节中的总体设计方案，为物料装填机器人各关节连杆建立坐标系，关节坐标系如图2所示。

图2 设计方案和关节坐标系示意图Fig.2 Design scheme of loading robot and schematic diagram of joint coordinate system

图2中，OkXkYkZk(k=0,1,…,5)表示各关节坐标系。b0表示沿X1轴方向，O1与O2的距离；b1表示沿Z4轴方向，O3与O4的距离；h0表示沿Z0轴方向，O0与O1的距离；h1表示沿X4轴方向，O4与O5的距离；L1表示关节2的位移；L2表示关节3的位移。

各关节坐标系定义过程如下：

1) 关节1坐标系O1X1Y1Z1:Z1轴沿转盘轴承的转动轴线方向，以关节2的直线运动方向建立Z2轴，Z1与Z2轴公垂线与Z1轴的交点为O1，公垂线方向为X1方向，根据右手定则确定Y1轴。

2)关节2坐标系O2X2Y2Z2：以关节3直线运动方向建立Z3轴，Z2轴与Z3轴的交点为坐标原点O2，X2轴垂直于Z2轴与Z3轴所构成的平面，根据右手定则确定Y2轴。

3)关节3坐标系O3X3Y3Z3：以关节4的转动轴线为Z4轴，Z3轴与Z4轴的交点为坐标系原点O3，X3轴垂直于Z3轴与Z4轴所构成的平面，根据右手定则确定Y3轴。

4)关节4坐标系O4X4Y4Z4：取Z4轴与转手连接板的对称平面交点为原点O4，X4轴与X3轴平行，根据右手定则确定Y4轴。

5)末端抓持器坐标系O5X5Y5Z5由坐标系O4X4Y4Z4沿X4方向偏置而得。

以坐标系O1X1Y1Z1为参照，将惯性坐标系O0X0Y0Z0固定在车内空间底部。

物料装填机器人的D-H参数如表1所示。

表1 物料装填机器人的D-H参数Tab.1 D-H parameters of loading robot

表1中：i表示关节编号;ai-1表示沿Xi-1轴，Zi-1轴移动到Zi轴的距离；αi-1表示绕Xi-1轴，Zi-1轴旋转到Zi轴的角度；di表示沿Zi轴，Xi-1轴移动到Xi轴的距离；Qi表示绕Zi轴，Xi-1轴旋转到Xi轴的角度。

使用ai-1、αi-1、di和θi4个参数可以得到(1)式所相邻连杆i与连杆i-1间的齐次变换矩阵Ai：

(1)

式中：Ri为连杆i与连杆i-1间的姿态矩阵，

(2)

Pi为连杆i与连杆i-1间的位置矩阵，

(3)

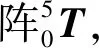
(4)

式中：R为物料装填机器人末端关节对车体空间的姿态矩阵；P为物料装填机器人末端关节对车体空间的位置矩阵。

2.2 工作空间分析

考虑到在执行物料装填任务时，机器人产生运动的关节为关节1、关节2、关节3和关节4，因此在进行工作空间分析中，令β3=0°.

物料装填机器人的正运动学方程转换为

(5)

(6)

(7)

关节1、关节2、关节3和关节4关节变量的取值范围如表2所示。

表2 关节变量的取值范围Tab.2 Value range of joint variables

基于表2中的数据，采用MATLAB软件计算得到物料装填机器人的工作空间如图3所示。图3中，蓝色区域为工作空间的三维展示，黄色区域为工作空间在O0X0Z0平面内的投影，橙色区域为工作空间在O0Y0Z0平面内的投影，紫色区域为工作空间在O0X0Y0平面内的投影。

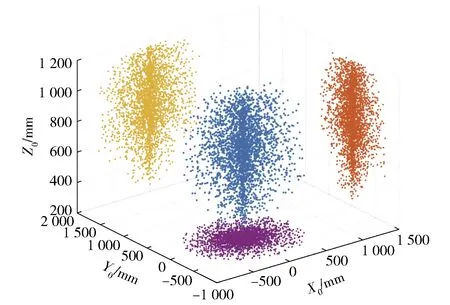
图3 工作空间Fig.3 Workspace

由图3可得，物料装填机器人末端可覆盖车体内部进行物料装填作业的空间，通过合理地规划运动轨迹，可以完成车内约束空间中的装填作业。

3 轨迹优化

根据第2节的分析结果可知，本文设计的物料装填机器人可以满足技术要求1和技术要求2. 考虑到基于多项式函数的关节轨迹曲线可以实现3阶导数连续，有利于减小因关节驱动力矩突变带来的冲击振动。本节以多项式函数对关节轨迹进行拟合，并使用粒子群优化算法对动作执行时间进行优化，使机器人满足技术要求3.

3.1 关节轨迹曲线构造

针对具有n个插值点的关节轨迹，需要有n-1段多项式函数拟合而成。在第j个插值点处(j≠0，n)，衔接的两段函数具有如(8)式所示的关系：

(8)

式中：hj(t)为t时刻多项式函数在点j处的取值。

(8)式表明，在各个插值节点处，关节的位移、速度、加速度和加加速度均连续，从而保证了各个插值节点处的关节轨迹连续平稳变化。

在关节轨迹的首尾插值点，即j=0与j=n的插值点位置，有(9)式所示的关系：

(9)

根据1.2节中对物料装填过程的阐述，考虑到关节2、关节3和关节4对物料位置和姿态的影响较大，对关节2、关节3和关节4的运动轨迹进行优化，关节2采用6个插值点进行轨迹拟合，关节3和关节4采用4个插值点进行轨迹拟合。轨迹插值点如表3所示。确定轨迹曲线的拟合方法如表4所示。

表3 轨迹插值点Tab.3 Trajectory interpolation points

表4 轨迹拟合方法Tab.4 Trajectory fitting method

表4中，“3-7-3”表示使用3次多项式函数构造第1段和第3段关节运动轨迹，使用7次多项式函数构造第2段关节运动轨迹，“3-5-3-7-3”轨迹拟合方法意义与“3-7-3”相同。

3.2 变量数目简化

考虑到关节轨迹曲线的系数总数十分庞大，会增加不必要的计算负荷，在优化前使用文献[15]中方法寻找变量间的关系，从而减少需要优化的变量数目。下面以关节3为例，说明变量转化方法。

关节3的轨迹具有4个插值点，以“3-7-3”的轨迹拟合方法拟合关节轨迹。“3-7-3”样条多项式的通式如(10)式所示：

(10)

式中：未知系数a11～a14、a21～a28、a31～a34分别表示关节轨迹第1段、第2段、第3段插值函数的系数；h1(t)、h2(t)、h3(t)分别表示关节第1段、第2段和第3段轨迹。

定义关节3初始点处的关节位置为x0，关节初始点速度为v0、加速度为A0；插值点j处关节位置为xj，末位点关节位置为x3，速度为v3，加速度为A3. 通过(8)式和(9)式可列出求解多项式系数的线性方程组，采用矩阵表示如(11)式所示：

M·a=b，

(11)

式中：M为与插值时间t1、t2、t3有关的矩阵；a和b分别为系数向量和约束向量，

用I2标准溶液制作工作曲线：配成3.20×10-2mol/L的贮备液，用时稀释10倍为标准溶液3.20×10-3mol/L。先在一系列50 mL比色管加入2.5 mL氯仿-冰乙酸（40∶60，V∶V），再分别加入I2标准溶液 0，0.10，0.15，0.20，0.25，0.30，0.40，0.50 mL，摇匀，然后各加入质量浓度为10 g/L的淀粉指示剂0.5 mL，加水稀释至刻度，塞进瓶塞，轻轻摇匀，静置5 min，待分层后取上层清液于波长535 nm处测定吸光度。根据其对应的浓度，绘制工作曲线。

(12)

由(11)式可得机器人轨迹函数的系数和插值点时间之间的关系为

a=M-1·b.

(13)

(13)式表明，可使用3个时间变量代替“3-7-3”轨迹方程中的16个系数。同理，可使用5个时间变量代替“3-5-3-7-3”轨迹方程中的26个系数，求解并优化关节4轨迹。

3.3 关节运动轨迹的优化求解

采用粒子群优化算法对插值时间进行优化，首先构建适应度函数。针对关节2、关节3和关节4的各个插值点，各关节轨迹曲线在两插值点间所拟合的多项式函数应满足：

yi,j(t)⊂[pi,j-1,pi,j]，t⊂[0,tj]，

(14)

式中：tj为关节i的轨迹在插值点j与插值点j-1之间的插值时间；yi,j(t)为关节i的轨迹在插值点j与插值点j-1之间拟合多项式函数的函数值；pi,j为关节i的轨迹中插值点j的位置。

关节i的轨迹在插值点j与插值点j-1之间拟合多项式函数的位置评价值如(15)式所示：

(15)

对于并行求解的关节2、关节3和关节4，3条轨迹曲线的位置评价总值如(16)式所示：

(16)

由于机器人关节轨迹必须满足运动学上的约束，ph必须为0. 考虑关节2、关节3和关节4的输入转速限制，线速度不应超过833 mm/s，角速度不应超过240°/s. 关节运动速度尽可能接近传动部件的额定速度，从而寻求时间上的最小量。关节i的轨迹在插值点j与插值点j-1之间拟合多项式函数的速度评价值如(17)式所示：

(17)

式中：vg表示关节的最高转速值。

并行求解3条轨迹曲线运动速度的速度评价总值如(18)式所示：

(18)

根据(16)式和(18)式，易得评价粒子的适应度函数fitness如(19)式所示。

fitness=λph+pv,

(19)

式中：λ为ph的权重。

确定粒子群优化算法的粒子描述与评价的适应度函数后，编制算法程序求解关节轨迹曲线。计算步骤如下：

1)在关节的插值时间5维搜索空间中随机生成m个粒子，每个粒子每个维度的取值区间为(0,ts]，以此得到种群pop，并初始化各粒子的速度，ts为每个粒子每个维度取值的最大值。

2)根据生成的m个粒子，计算得到系数矩阵a.

3)检查a是否满秩，如果不满秩，则重新生成粒子m.

4)由系数矩阵确定关节轨迹的多项式函数。

5)使用(15)式和(16)式计算每次迭代中每个粒子产生的ph，以使ph值最小为标准选择最佳值和群组最优值。更新粒子种群并迭代计算，找到使ph值最小的粒子。

6)若ph为0，则进入步骤7，否则将ts更新为ts+dt，进入步骤1，dt为时间步长。

7)对关节轨迹函数求导，得到各轨迹的速度值。

8)使用(19)式计算每次迭代中每个粒子的适应值fitness，以fitness最小为标准选择最佳值和群组的最佳值，迭代计算，找到使fitness值最小的粒子。

9)完成优化。

3.4 关节运动轨迹优化结果分析

应用MATLAB软件编制相应的优化算法程序。优化时，粒子初始搜索区间为(0,0.6],dt=0.5 s，初始化粒子速度随机取值区间为[-1,1]，粒子种群规模为50个，迭代次数800次，位置变异概率为0.2，权重值λ=1 000.

适应度函数fitness值随迭代次数变化如图4所示。由图4可知，200步后，适应度函数不再发生明显变化，可认为算法已找到全局最优解。

图4 适应度的迭代变化Fig.4 Iterative change in fitness

优化前后的参数对比如表5所示。

表5 优化前后的参数对比Tab.5 Comparison of parameters before and after optimization

注：t1～t5分别为第1～第5段轨迹的插值时间。

搭建物理样机对优化结果进行校验。物理样机关节2、关节3和关节4驱动装置的相关参数如表6所示，其中电机均为溧阳宏达电机公司生产。实验结果如图5所示。

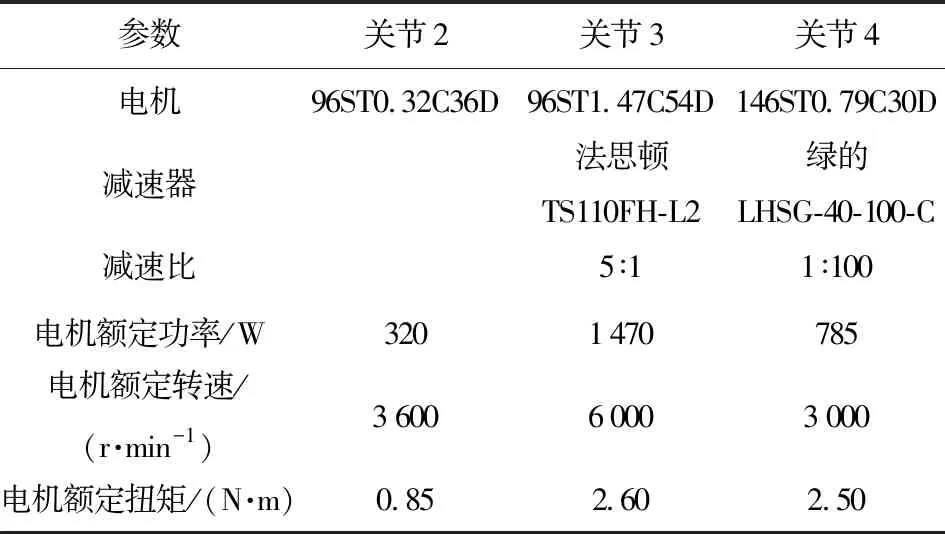
表6 驱动装置参数Tab.6 Parameters of actuator

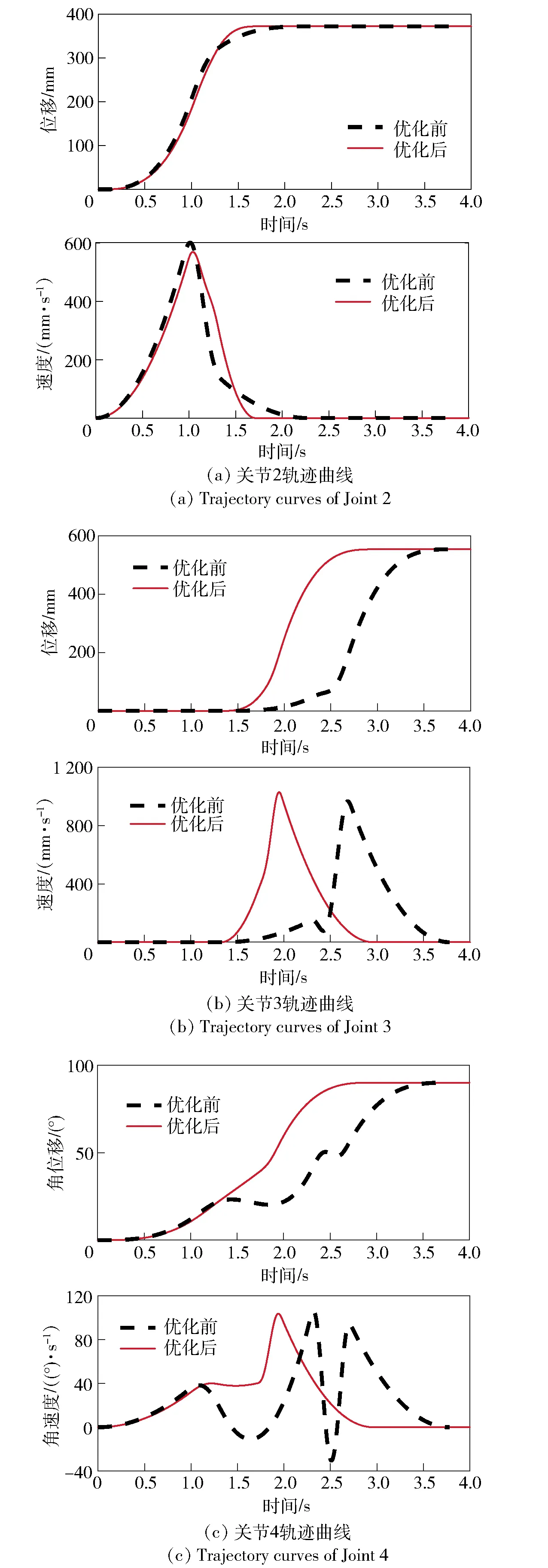
图5 关节轨迹曲线Fig.5 Joint trajectory curves

由上述分析结果可得，优化后关节运动总时长由3.78 s减小为2.97 s，满足技术要求3. 同时，优化后，各关节在运动过程中的速度变化更为连续平稳，关节2最高速度为571 mm/s，关节3最高速度为1 031 mm/s，关节4最高角速度为103°/s，均不超过各关节驱动装置的额定转速。

4 结论

1)本文提出一种“RPP-RR”构型的物料装填机器人，该机器人使用平动关节代替转动关节完成物料在竖直平面内的搬运，使得机器人结构紧凑，可在狭小空间内完成装填作业。

2)给出该型物料装填机器人的正向运动学模型，并仿真计算其工作空间，计算结果表明该型机器人具有较高的空间利用率，其工作空间可包络车内所有作业空间，

3)构造脉动连续轨迹曲线，提出使用插值时间变量代替系数变量的方法，并采用粒子群优化算法优化关节轨迹。优化后关节运动时间减小约21.4%，优化后轨迹曲线可在3 s内完成一次装填作业，满足快速、平稳装填的要求。