无线自组织网络协作时间同步优化算法

刘大鹍， 陈桂芬， 王义君

(1.长春理工大学 电子信息工程学院， 吉林 长春 130022; 2.中国北方车辆研究所 网络与信息中心， 北京 100072)

0 引言

无线自组织网络通常布置在具有一定面积的局部范围之内，由若干信息采集及传输节点组成，该网络采用无线通信方式且能够动态组网，具有多跳通信及移动性等特点[1]。在军事应用领域，不论是集群单兵作战系统还是无人平台协作攻击及防护系统，都可认为是无线自组织网络的一部分。其目的是通过动态路由和移动管理技术传输具有服务质量要求的多媒体信息流，一般节点需要具有持续的能量供给[2]。从目前看，无线自组织网络的关键技术包括射频识别技术、无线传感器网络技术、智能嵌入技术、自组织管理技术以及安全技术等[3]。但是对于绝大多数应用场景，尤其是军事领域，如果能够通信的网络节点不能有效实现时间同步，那么很多应用将变得没有意义。因此无线自组织网络时间同步技术的研究是未来军事及民用领域能够实现广泛应用的技术基础。无线自组织网络中的节点只有实现精确的时间同步，才能保证目标跟踪、定位、拓扑控制等技术得以有效实现[4-6]。

目前，众多学者对于无线自组织网络时间同步技术进行了较为深入的研究。文献[7]提出一种基于相位同步的最小生成树分析方法。该方法通过相位同步建立不同时间序列之间的相关性，主要包括相互关联、 线性和非线性。同时，在这种方法中，一对时间序列 (节点) 之间的链接强度是由它们之间的相位同步级别决定的，利用非线性相关经济时间序列实现同步分析。文献[8]提出了面向无线传感器网络的快速精确、能量有效的时间同步协议。该协议的设计用于恶劣环境，并基于电阻式电网的思想。通过协议的执行可以产生高质量时间估计，在整个通信周期中保证时间同步的准确性。文献[9]针对无线传感器网络经典同步算法稳定性较差等问题，提出一种基于频率偏差估计的时间同步算法。该方法通过低开销相位偏差和频率偏差估计方法，结合分层和广播监听构建响应的同步策略，可有效地平衡同步能耗、同步精度及同步稳定性。针对同步精度对随机延迟和时钟速率波动敏感等问题，文献[10]将成对同步误差建模为随机延迟和时钟漂移的功能函数，并以定量的模型同步性能作为相关参数的函数衡量指标，同时，针对不同对等同步方案分析了同步误差。文献[11]针对时间误差的累积以及节点多跳传输能量损耗等问题，提出基于移动参考节点和最优移动路径的时钟同步方法。该方法首先选取时钟同步节点，然后建立数学模型，最后通过标记时间戳建立单跳同步机制，提高同步时间精度同时，降低了通信能耗。

本文在上述研究基础上提出无线自组织网络协作时间同步优化算法(CTSOA)。该算法在时间同步信号模型和基于接收端- 接收端的同步机制模型基础上，利用指数延迟模型，通过对成对节点的时钟偏移及时钟漂移进行联合估计提高时钟同步精度；对网络进行三角剖分，利用拓扑结构的自适应变化实现全网节点时钟同步；通过协作时间同步优化算法的整体执行，保证链路时延及网络能耗的降低。仿真结果表明，在本文提出的三角剖分拓扑结构控制下，与传统分簇拓扑相比，CTSOA在平均同步误差、同步算法能量消耗方面取得了一定的改进。

1 时间同步模型

无线自组织网络中每个节点相互链接，通过多跳路由完成信息传输。大多数情况下，只有网络节点的时间精度满足一定的范围要求，才能实现无线自组织网络的应用，因此每个网络节点都遵循自身的本地时钟，而晶振的频率和阈值决定了时钟同步的解决方式。本文所设计及采用的时间同步模型主要包括时间同步信号模型及接收端- 接收端同步机制模型。

1.1 时间同步信号模型

对于接收端- 接收端时间同步方法，接收侧的时间延迟是时间同步误差的重要来源[12]。其最大特点是使关键路径上的发送时间延迟和访问时间延迟得以消除。传输时延示意图如图1所示。

图1 传输时延分析Fig.1 Transmission delay analysis

令网络节点的本地时钟为T(t)，t为理想参考时间。由于晶振的不确定性，第i个节点的时间模型可以定义为

Ti(t)=ωit+φi+εi，

(1)

式中：ωi为时钟漂移(或频率偏差)；φi为时钟偏移(或相位偏差)；εi为随机噪声。此时，网络中2个节点(节点1和节点2)间的时钟关系可以表示为

T1(t)=ω12T2(t)+φ12+εi，

(2)

式中：ω12和φ12分别为节点1和节点2间的相对时钟漂移系数和相对时间偏移。因此，当ω12=1、φ12=0 μs时，两个节点将完全实现时间同步。如果网络中有N个节点，则当Ti(t)=Tj(t)时，整个网络将实现全局同步，i,j=1,…,N.

时钟偏移估算是时间同步算法中非常重要的一个环节。Elson等[13]通过实验证明接收端任意两个节点间本地时间差的时钟偏移符合μ=0、σ=11.1 μs的高斯分布，其中，μ为时钟漂移系数，σ为相对时间偏移。本文仿真拟合出的最佳参数结果为μ=0.048、σ=11.221 μs，统计学分布图如图2所示。该实验结果对于后续算法的实现具有重要指导作用。

图2 时钟偏移统计学分布Fig.2 Clock offset statistical distribution

1.2 通信模型

自组织网络中异构网络结构不同，对于传输对象的信号带宽也不尽相同，每个节点必须能够感知信号的频带宽度，用以完成对网络的选择和信号的传输。在实际应用中，当被监测区域中的监测对象不在节点的通信范围之内时，节点则不能感知到监测对象，此时还需考虑发射功率对于接收节点的影响。

根据电磁波传播理论，当其在自由空间中传播时，如果发射端与接收端在视距范围之内，则可用自由空间传播模型预测接收信号的强度。如果发射端的信源发射功率为PT，则收发节点之间的信号功率关系为

(3)

式中：PR为信宿接收功率；λ为载波波长；r为收发端的距离；AT、AR分别为信源天线和信宿天线的增益；δ为信道衰落系数。

1.3 接收端- 接收端同步机制模型

图3 接收端- 接收端同步机制模型Fig.3 Receiver-receiver synchronization model

接收端- 接收端同步机制模型如图3所示。节点R表示参考节点，为发送端节点，负责初始化同步协议，并向在其通信范围内的接收端节点S和M广播信标包，其中：节点M为主节点，该节点与参考节点R实现双向通信，接收节点R发送的广播信标包，并向节点S发送同步信息；节点S为从节点，通过接收参考节点R的广播信标包和主节点M同步信息完成自身的同步误差修正，实现与主节点M的时间同步。接收端两节点通过记录每一轮同步信标包中的时间戳，完成对于时钟偏移和时钟漂移的相应估计，节点M修改自己的时间偏移来完成一次时间同步。随着时间同步周期次数的增多，节点S通过周期性地接收节点R与节点M的双向信息，不断地调整自己的同步延迟，使自身与节点M时间同步。

2 时间同步算法

针对目前无线自组织网络时间同步算法同步精度低、能量消耗大等问题[14-15]，提出无线自组织网络协作时间同步优化算法。本算法利用指数模型，通过对成对节点的时钟偏移及漂移进行联合估计来提高时钟同步精度；利用拓扑结构的自适应变化实现全网节点时钟同步；通过协作时间同步优化算法的整体执行，保证链路时延及网络能耗的降低。

2.1 成对节点时钟漂移及时钟偏移的联合估计

图4给出了主节点与从节点间时间信息交互的时钟漂移与时钟偏移模型。如图4所示，M为主节点，S为从节点，主节点记录第m轮信息交互的时间戳TM1、TM4，从节点记录第m轮信息交互的时间戳TS2、TS3. 主节点传输同步包给从节点，该同步包中包含主节点的本地时间戳TM1，从节点在TS2接收到该同步包并且在TS3发出一个应答包，主节点在TM4接收到该应答包。该过程中，从节点的时间模型可定义为

TS2=(TM1+td)ω+φ+ΓS2，

(4)

TS3=(TM4-td)ω+φ+ΓS3，

(5)

式中：td为传播过程的固定时延；ω为时钟漂移；φ为时钟偏移；ΓS2、ΓS3一般为符合高斯分布的随机噪声。

图4 时间信息交互模型Fig.4 Timing message exchange model

由上述模型，给出一种指数模型估计的一般似然函数形式：

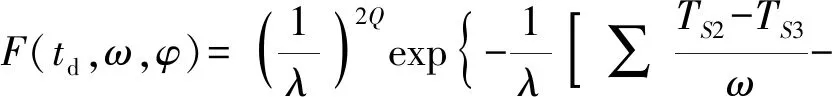
(6)

式中：Q为循环周期；辅助函数L定义为

(7)

由(6)式可知，如果将随机噪声忽略，与时钟估计相关的参量只有固定时延td，该参量一般可以通过消息包信息交换计算得出，但必然会增加网络能耗。因此，在上述模型基础上，不计算固定时延，认为其为未知量，在此条件下估算ω及φ值。

因为td和φ均未知，所以其定义域可限制为

(8)

统计因子E可表示为

(9)

式中：k为循环轮次。

(10)

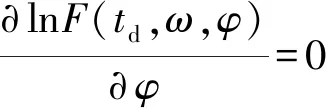
(11)

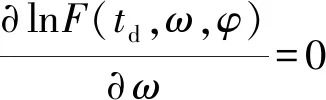
(12)

2.2 自适应全网络同步

2.2.1 参考节点确定

假设网络覆盖区域为C，采用计算几何的方式选取参考节点。将区域C划分为u个单调多边形，目的是通过引入对角线消除多边形不规则情况下引起的拐点。设点p为一拐点，与其连接的2条多边形的边为向下方向，则此时需构造1条以p为起点向上连接的对角线，该对角线将原多边形分为2部分，此时p不再属于拐点，而属于划分后2个多边形的1个顶点，基于此完成区域C的单调划分。然后，按随机次序依次引入网络中的各节点，维护程序的执行并更新一个与当前点集对应的三角剖分。基于三角剖分的网络区域划分算法流程如图5所示。

图5 网络区域划分算法

Fig.5 Network region division algorithm

通过对覆盖区域的外部多边形结构进行单调划分和三角剖分，图6给出了无线自组织网络内有50个节点时在平面区域内划分的三角剖分拓扑结构图。

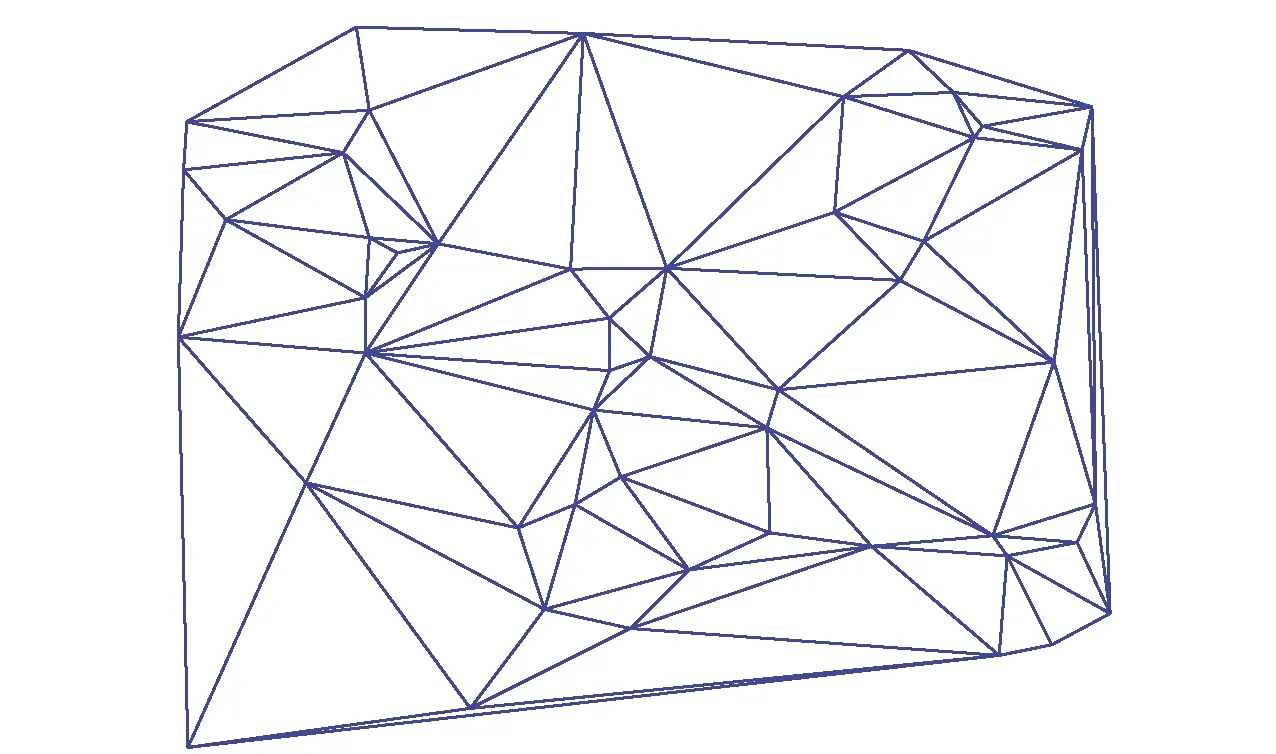
图6 经过三角剖分后的网络拓扑结构Fig.6 Network topology after triangulating

经过三角剖分的拓扑结构形成后，令三角形顶点处的节点组成一个子集。为了最大限度地在该子集中找到尽可能少的节点、完成区域覆盖任务，使用红、黄、绿3种颜色给子集中的所有节点进行染色。染色方案需满足由任何边连接的2个节点，所染的颜色不能相同。基于此，经过三角剖分的多边形经过染色后，其中每个三角形都有且仅有1个红色、黄色和蓝色的顶点。通过上述方法，当网络完成三角划分后，选择划分好的三角形中质心点位置节点作为参考节点，该节点需覆盖所在三角区域的通信距离。参考节点选择示意图如图7所示。

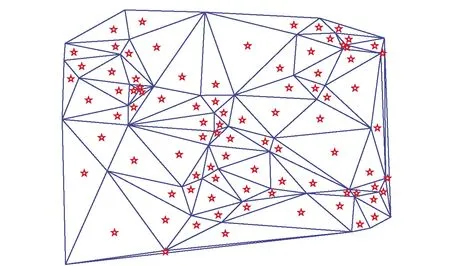
图7 参考节点选择示意图Fig.7 Reference node selection

2.2.2 多跳自适应拓扑结构建立

成对节点同步需要扩展到全局多跳范围网络自适应同步，而如果要实现全网同步，必须建立有效的网络拓扑结构。下面通过构建一种基于参考节点的局部树形网络来实现节点的自适应同步。网络拓扑结构图如图8所示。

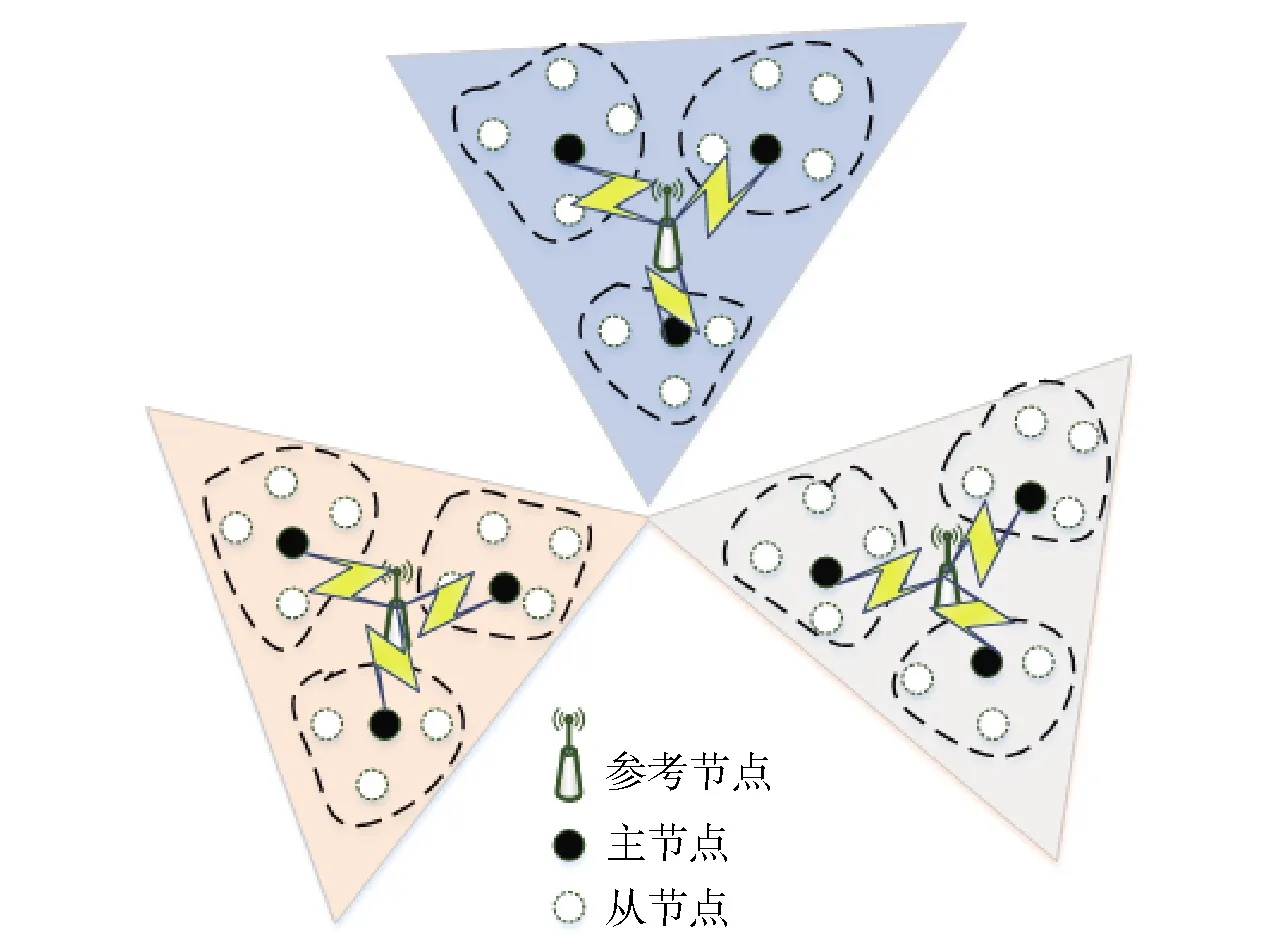
图8 网络拓扑结构图Fig.8 Network topology

首先，建立参考节点与主节点同步网络。当通过三角剖分及染色选择出每个三角形区域的参考节点后，该参考节点即为该区域的主同步节点，同时为树形网络的根节点，将其本地时间作为网络的参考时间。此时，参考节点进行第1轮消息广播，该范围内所有节点通过比较自身链路能量、误包率和时间延迟的权重，计算出归一量化值，并与预先设定的阈值进行对比，高于预设阈值的节点均可作为该范围内的主节点。时间延迟、误包率和自身链路能量的计算公式分别为

(13)

PER=1-PERC，

(14)

(15)

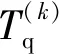
其次，建立主节点与从节点同步网络。在同一参考节点覆盖的区域内，主节点确定后，其余所有节点均为从节点。当参考节点第2轮广播消息结束后，从节点与主节点同样，都会记录下参考节点的时间戳信息。然后所有主节点均广播已调整后的本地时间戳信息，从节点感知到信息后，仅会选择第1个接收到的主节点信息，然后将不再接收其他主节点信息。此时，从节点根据接收到的主节点时间戳信息和参考节点时间戳信息进行时钟偏移和漂移的估计。

第三，对于网络边缘的节点，有时可以接收到多个三角剖分区域的参考节点和主节点消息，此时将这类节点称为同步辅助节点。该节点同时处在多个参考节点的通信范围内，可以与参考节点进行双向通信实现同步。其主要作用是作为参考节点同步的一个补充，能够进一步协调参考节点间的同步精度。

整个网络中通过三角剖分划分区域，并通过染色确定参考节点，参考节点选取主节点，从节点与主节点实现同步。参考节点的时间为基准时间，能否准确地将网络标准时间同步至全网络，是至关重要的。该拓扑结构防止了单一节点突发性失效和被干扰等因素，从而影响到整个网络的同步性能。CTSOA流程如图9所示。

图9 CTSOA流程图Fig.9 CTSOA flow chart

3 仿真结果及分析

在500 m×500 m区域内布置500个自组织协作网络节点通过仿真计算验证时间同步算法，具体仿真设置参数如表1所示。为了验证本文提出的CTSOA有效性，将其与文献[8]提出的有效单跳时间同步(ESTSP)算法、文献[12]提出的能量有效参考广播同步(ERBS)算法、文献[13]提出的参考广播同步(RBS)算法进行比较，前提是将4种算法同时置于表1所示仿真环境下进行实验，并对本文所提三角剖分拓扑结构和传统分簇拓扑结构下的同步参数进行对比。主要在平均同步误差、能量消耗两个方面进行数据处理和分析，而同步包数量和同步收敛时间的分析则可以更好地说明本文算法在精度和能耗方面的优势。

首先，本文对4类算法的平均同步误差进行仿真验证，仿真结果如图10所示。图10(a)为采用本文提出的三角剖分拓扑结构仿真得到的平均同步误差数据结果，可见同步周期越长，同步时间戳数据越精确，同步误差越小。由于CTSOA采用时钟漂移和时钟偏移的联合估计，相较于其他3种算法，其平均同步误差最低，小于100 μs. ESTSP算法的平均同步误差约为200～100 μs之间，ERBS算法的平均同步误差约为300～200 μs之间，而RBS算法的平均同步误差最大，大于600 μs. 图10(b)为采用传统分簇拓扑结构仿真得到的4类算法平均同步误差实验数据，通过与图10(a)对比可知：其平均同步误差要比三角剖分拓扑结构时均有所增加；尽管CTSOA效果最好，但是其平均同步误差仍然在200～100 μs之间。

表1 仿真参数Tab.1 Simulation parameters

图10 平均同步误差Fig.10 Average synchronization error

图11 能量消耗Fig.11 Energy consumption

其次，对4类算法的能量消耗进行仿真验证，仿真结果如图11所示。图11(a)为采用本文提出的三角剖分拓扑结构仿真得到的能量消耗数据结果，可见参考节点数越多，网络规模越大，能量消耗越高。由于CTSOA采用自适应拓扑控制，相较于其他3种算法，其能量消耗最低，约为200 mW左右。ESTSP算法的能量消耗比CTSOA略高，ERBS算法的能量消耗在400 mW左右，而RBS算法的能量消耗最高，在500～600 mW之间。图11(b)为采用传统分簇拓扑结构仿真得到的4类算法能量消耗实验数据，通过与图11(a)对比可知：其能量消耗要比三角剖分拓扑结构均有所增加；CTSOA和ESTSP算法效果相差不多，但是它们的能量消耗仍然在500 mW左右。

第三，采用两种拓扑结构对CTSOA同步包数量进行仿真验证，仿真结果如图12所示。由图12可见，随着网络节点数量的增多，在时钟联合估计和自适应三角剖分拓扑控制的基础上，CTSOA的同步包数量明显少于分簇拓扑结构时的同步包数量，证明了该算法的整体执行对于网络开销及系统稳定性均有所提升。

图12 同步包数量比较Fig.12 Comparison of the number of synchronization packages

最后，采用两种拓扑结构对CTSOA同步收敛时间进行仿真验证，仿真结果如图13所示。由图13可见，随着网络节点数量的增多，在时钟联合估计和自适应三角剖分拓扑控制的基础上，CTSOA的平均收敛时间约为3.28 s，而采用分簇拓扑结构的平均收敛时间约为6.21 s，由此可以看出，本文算法在收敛时间上得到较大幅度提升，具有较好的收敛性。

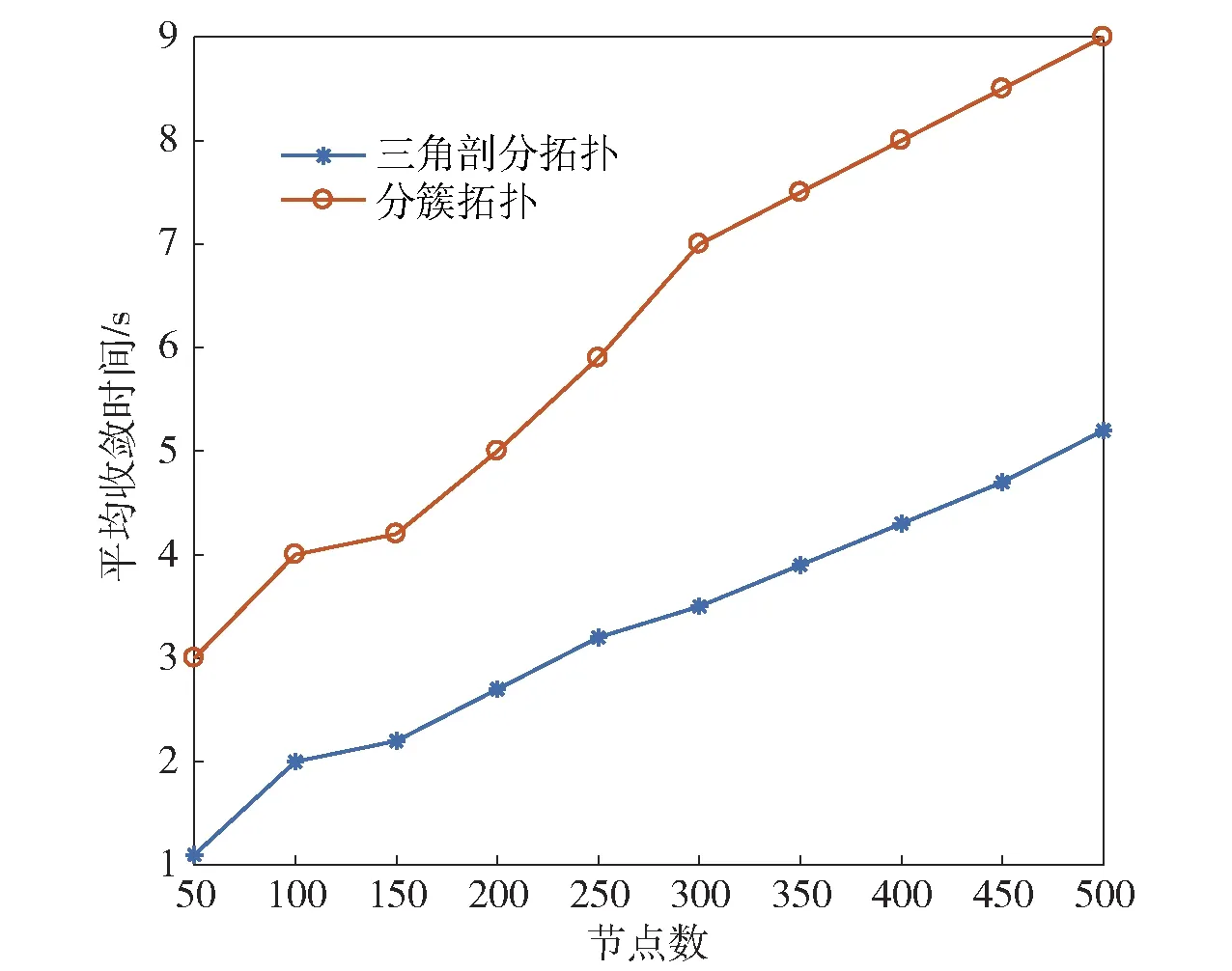
图13 收敛时间比较Fig.13 Comparison of convergence times

4 结论

本文在分析无线自组织网络时间同步算法存在问题的基础上，提出无线自组织网络协作时间同步优化算法。该算法主要利用时钟偏移和时钟漂移的联合估计及三角剖分的自适应网络拓扑控制实现时间同步算法优化。相较于其他算法，该算法平均同步误差较小，能量消耗较低。同时，将该同步算法应用在本文提出的三角剖分拓扑中，结果表明：相较于分簇算法，在同步包数量和平均收敛时间两方面都取得了较好效果。虽然仿真实验证明了CTSOA的有效性，但本文在节点具有移动特性的情况下，相关性能指标优势并不明显。后续研究将节点移动性的时间同步技术作为研究重点，研究无线自组织协作网络的覆盖定位问题，从根本上提升无线自组织网络在单兵作战系统，以及异构无人平台数据传输速率和可靠性等方面的应用效率。