气体与液体两相连续旋转爆轰波二维数值模拟研究
王放, 翁春生, 武郁文, 白桥栋, 郑权
(南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094)
0 引言
爆轰是一个由强反应激波诱导的燃烧过程,它与传统的等压燃烧相比具有更高的热效率[1]。基于爆轰燃烧的发动机还具有结构紧凑、推重比大的优点。连续旋转爆轰发动机(RDE)是一种利用一道或多道爆轰波在环形燃烧室内连续传播从而产生推力的发动机,近年来已成为国内外学者研究的热点。燃料和氧化剂通常采用分开喷注方式从头部的环缝或者孔进入燃烧室,连续旋转爆轰波(RDW)在燃烧室头部周向传播,传播方向与燃料喷注方向垂直,高压爆轰产物侧向膨胀,通过喷管排放到大气中产生推力。
实验研究方面,俄罗斯Bykovskii等[2-3]使用不同燃料(包括氢气、甲烷、丙烷、煤油、汽油等)在多种尺寸RDE上进行了大量实验,获得两相RDW结构如图1所示。魏万里等[4]通过实验研究了氧化剂喷注面积对气态RDE的影响。文献[5-6]成功起爆了汽油与富氧空气RDE,获得的RDW波速为1 022.2~1 171.8 m/s.
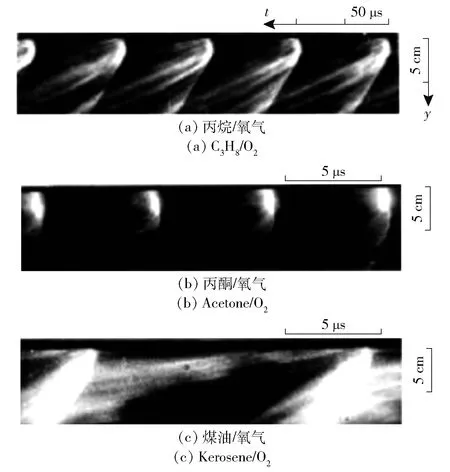
图1 实验所得不同燃料下RDW结构[2]Fig.1 Experimental results of RDW structure with different mixtures[2]
数值模拟研究方面,国内外学者对气态燃料RDE进行了广泛深入的研究,取得了丰富的成果。Liu等[7]使用5阶加权本质非振荡(WENO)方法和9组分化学反应模型对H2/Air RDE进行了数值模拟,发现了低频不稳定性和高频不稳定性同时存在于单波和双波模态RDW的现象。Fujii等[8]通过non-MUSCL-type 2阶迎风方法研究了C2H4和O2喷射条件对RDW波速的影响,发现在非匀混进气条件下已燃气体对RDW波速有着重要的影响。Sun等[9]使用ANSYS/Fluent软件研究了非预混进气条件的H2/Air RDE,发现空气喷孔宽度和总质量流量会影响RDW的传播模态,RDW的自持传播需要较高的总质量流量。以上研究揭示了气态燃料RDW流场结构演变规律,分析了气态燃料旋转爆轰的特性。李宝星等[10-11]用结构化网格守恒元与求解元(CE/SE)方法对汽油与富氧空气两相爆轰进行了数值模拟,获得了单波模态RDW的爆轰特性。目前国内外学者关于液态燃料RDW的数值研究较少,缺少对于气体与液体(简称气液)两相连续旋转爆轰流场结构和爆轰特性的认识。
非结构化CE/SE方法最早由Chang[12]提出,Shen等[13-14]拓展了非结构化CE/SE方法,获得了很好的计算结果。Nisar等[15]提出了新的守恒元和求解元分裂方法。这些研究带来了非结构化网格CE/SE方法研究的热潮。非结构化CE/SE方法除了具有计算格式简单、精度高、捕捉间断能力强等优点外,还可以灵活划分计算域内的网格,在三维复杂流场计算上更具潜质。目前还没有发现该方法用于计算气液两相连续旋转爆轰的文献报道。
为了解决气液两相旋转爆轰数值计算问题,探究气液两相旋转爆轰的流场结构和爆轰波参数变化规律,本文利用非结构化三角形网格CE/SE方法计算汽油与空气两相旋转爆轰过程,开展并行化程序设计,计算在不同当量比和不同进气总压下的RDW传播特性,获得两相RDW不同模态的流场结构,分析不同模态RDW的工作特性。
1 物理模型
1.1 计算模型
由于RDE燃烧室的厚度通常远小于其半径,为方便计算,径向气流变量可以忽略,RDE的数值计算可以简化为二维问题[16-18]。 沿着环形燃烧室的1条母线剪开,可以得到二维矩形计算区域。
如图2所示,计算区域为长0.3 m、宽0.1 m的矩形计算域。左右两边是周期边界,参数可以在二者之间互换。上边界是无反射出口边界,当出口速度为超声速时,出口边界参数由2阶外推得到;当出口速度为亚声速时,出口边界辅助网格的压力和温度分别为0.1 MPa和298 K,其余物理量包括密度、周向速度和轴向速度均与边界网格相同。下边界为入口边界, Schwer等[19]以及Frolov等[20]已经表明燃烧产物很少穿透至上游,因此此入口条件也忽略了回火的影响。入口边界各参数包括压力、温度和喷射速度由等熵流动计算所得,即将每个网格点视为等截面流管,入口参数根据当地压力和入口总压由等熵流动关系计算。设燃烧室内入口头部的压力为ph,燃料喷射总压和总温分别为p0和T0,壅塞条件下临界压力为
(1)
式中:γ为比热比。根据ph和p0的大小关系,入口边界的压力p、温度T和轴向速度v的赋值可以分为以下3种情况:
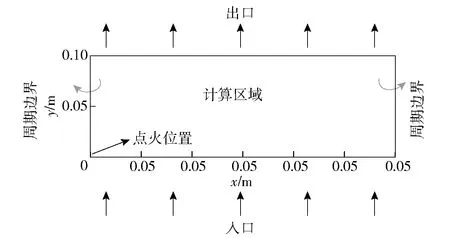
图2 计算区域示意图Fig.2 Computational domain
1)若ph≥p0,则新鲜燃料停止喷射,入口边界设为固壁边界;
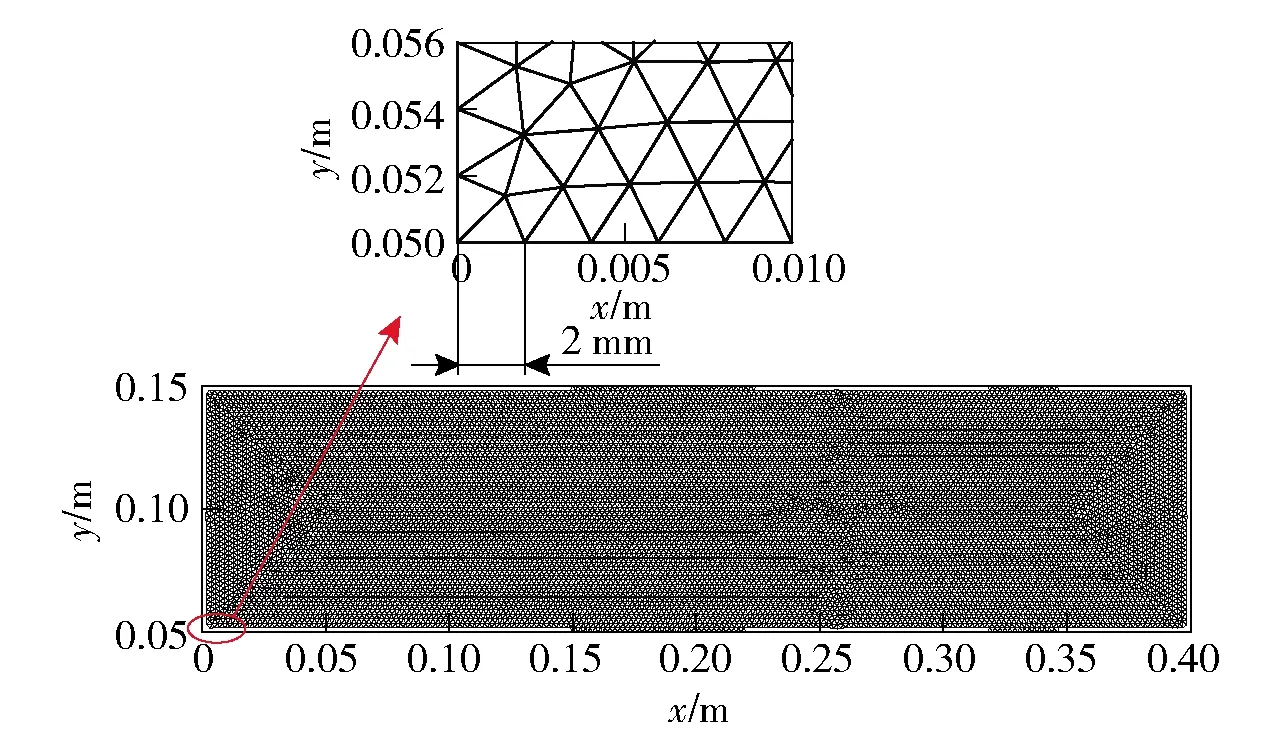
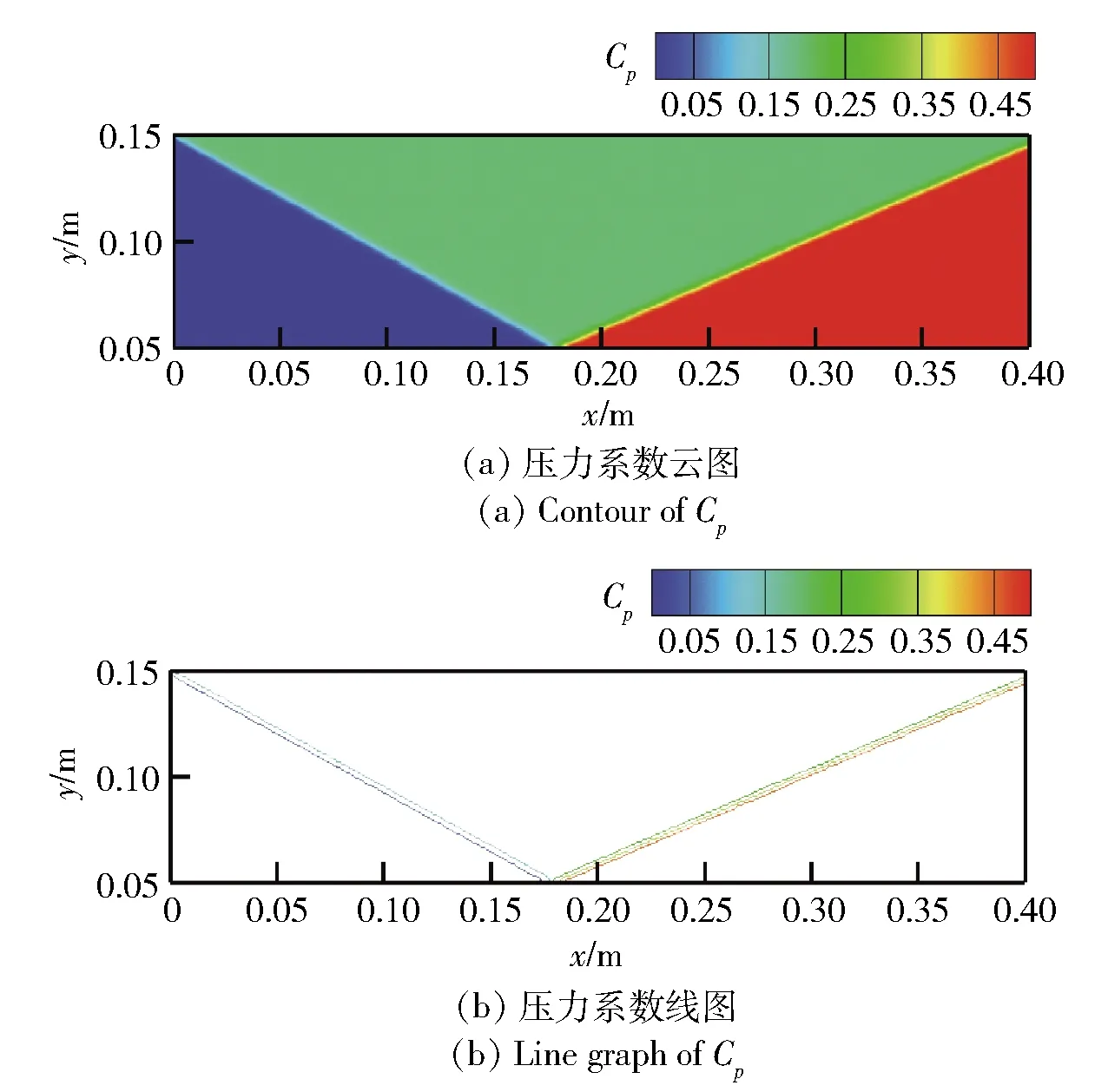
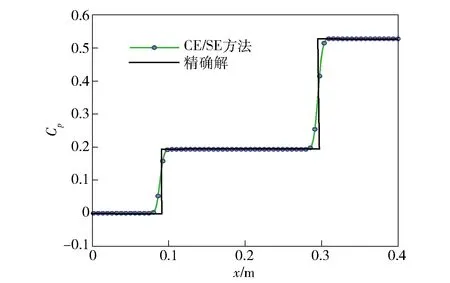
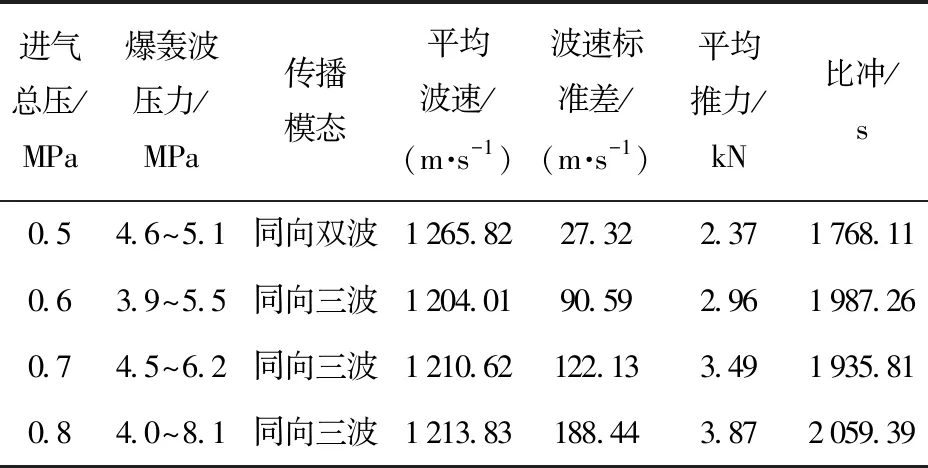
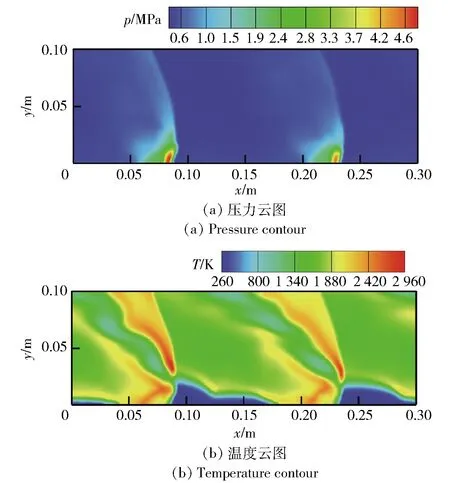
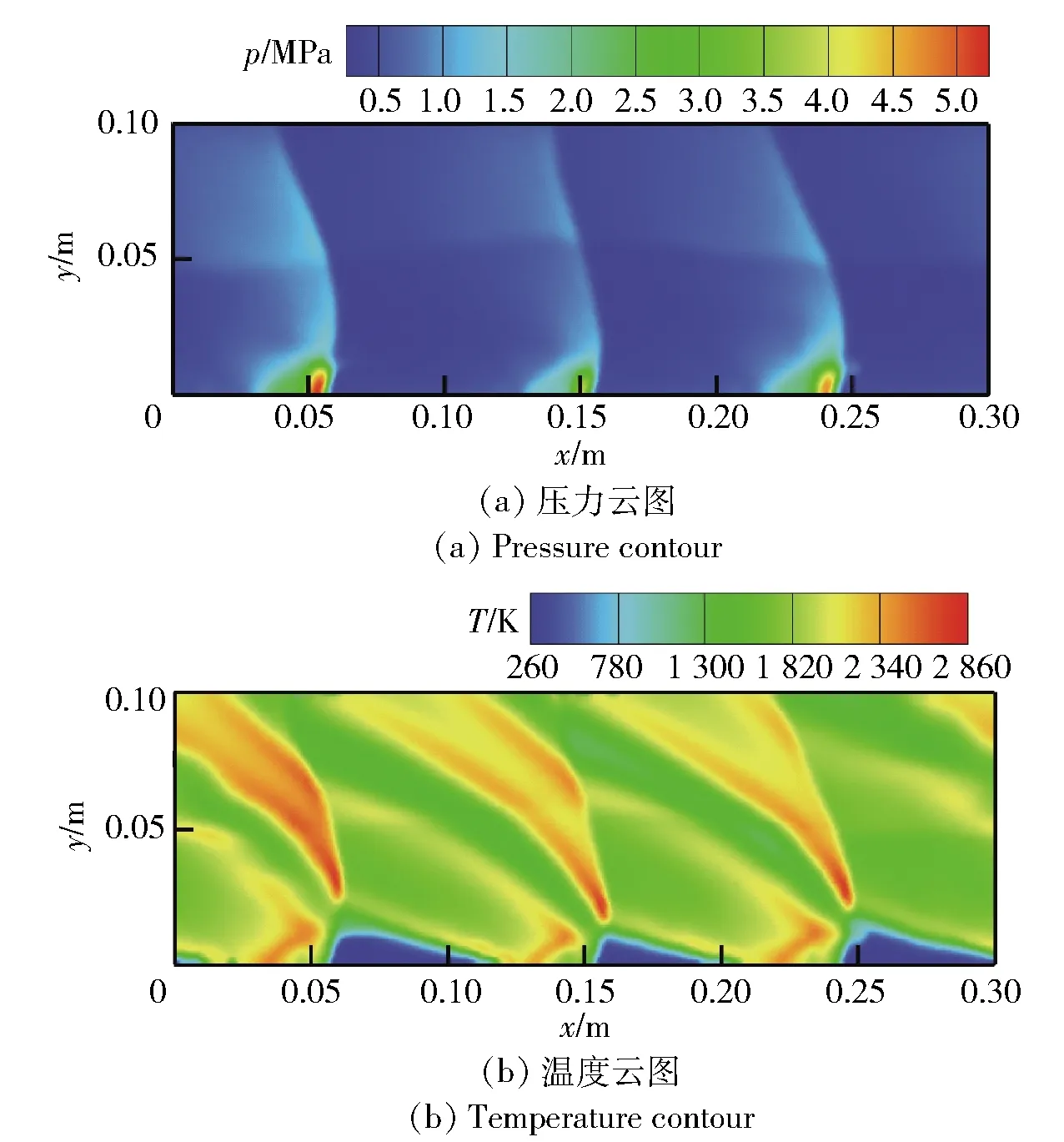
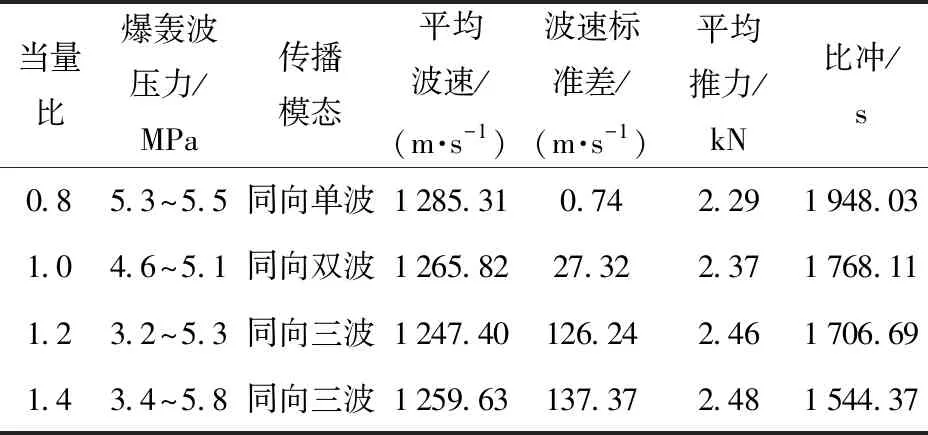
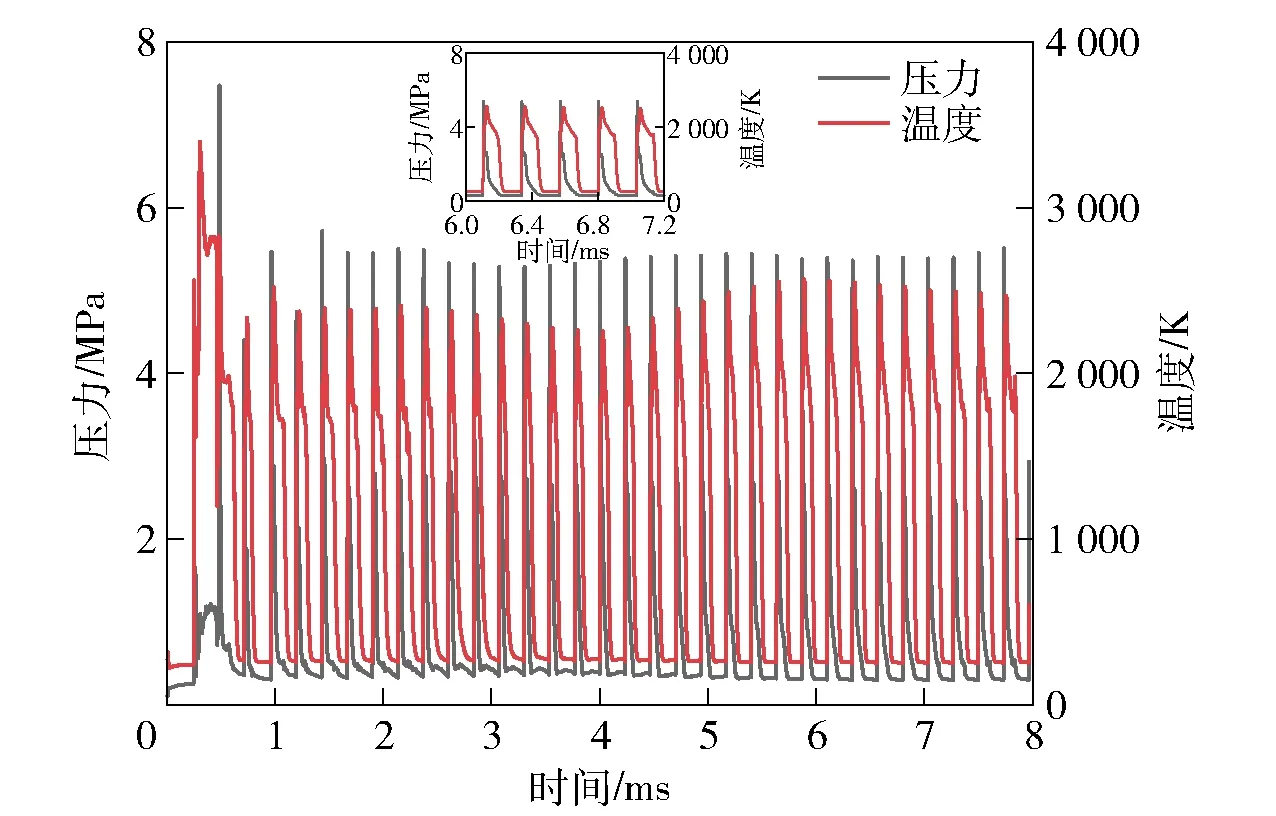
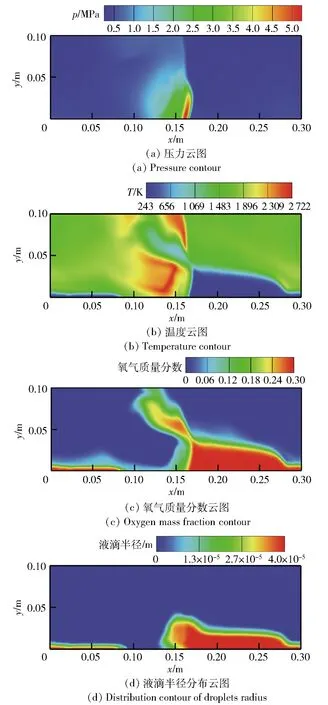
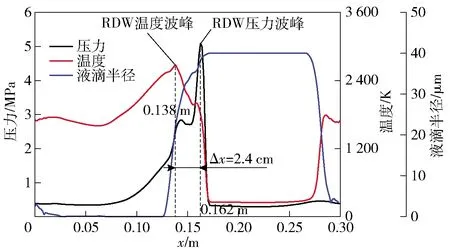
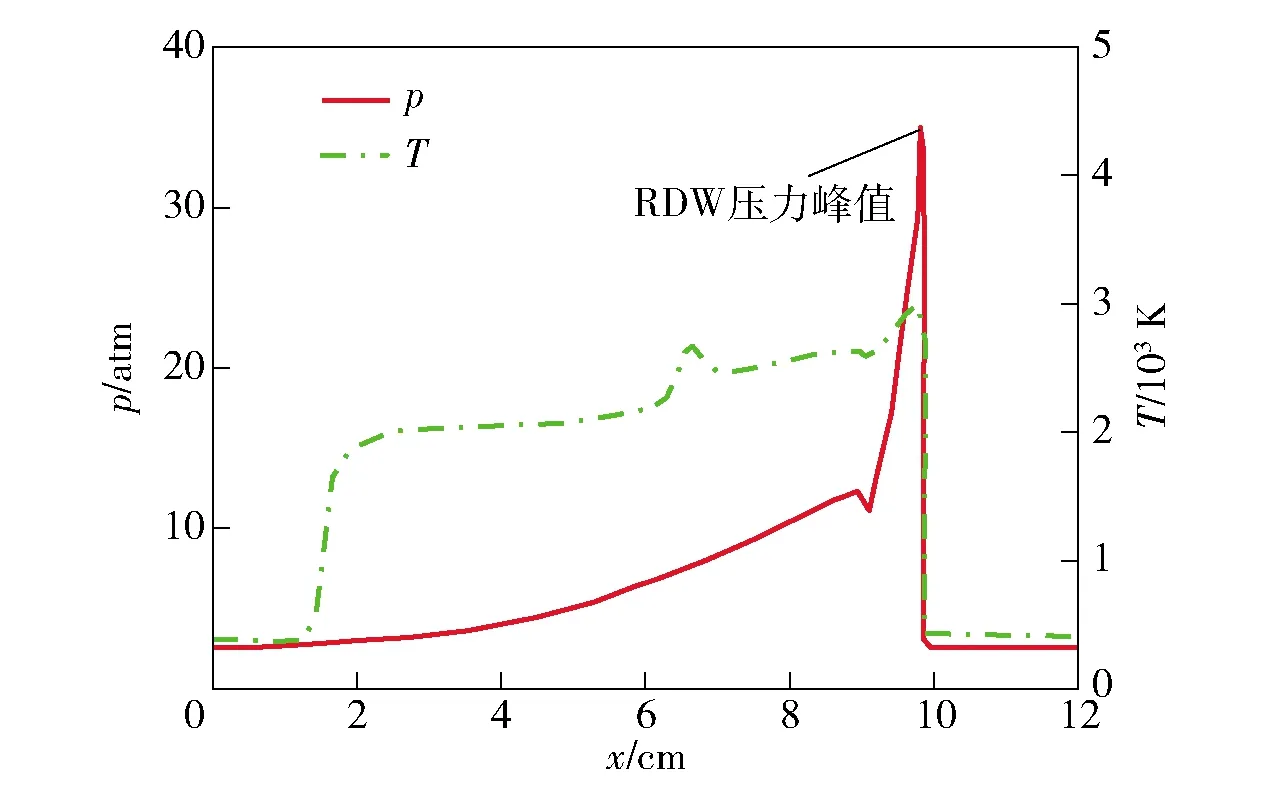
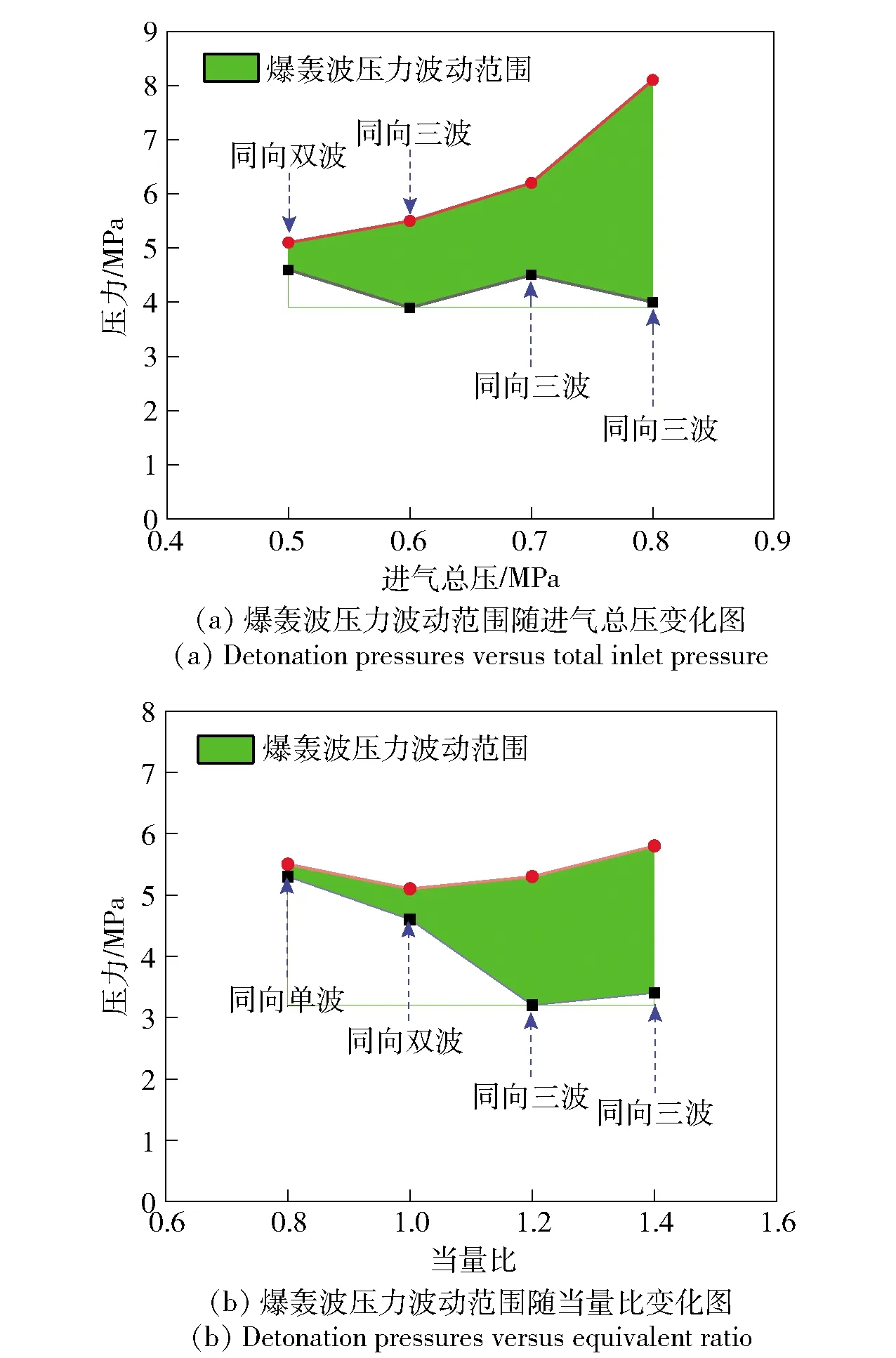
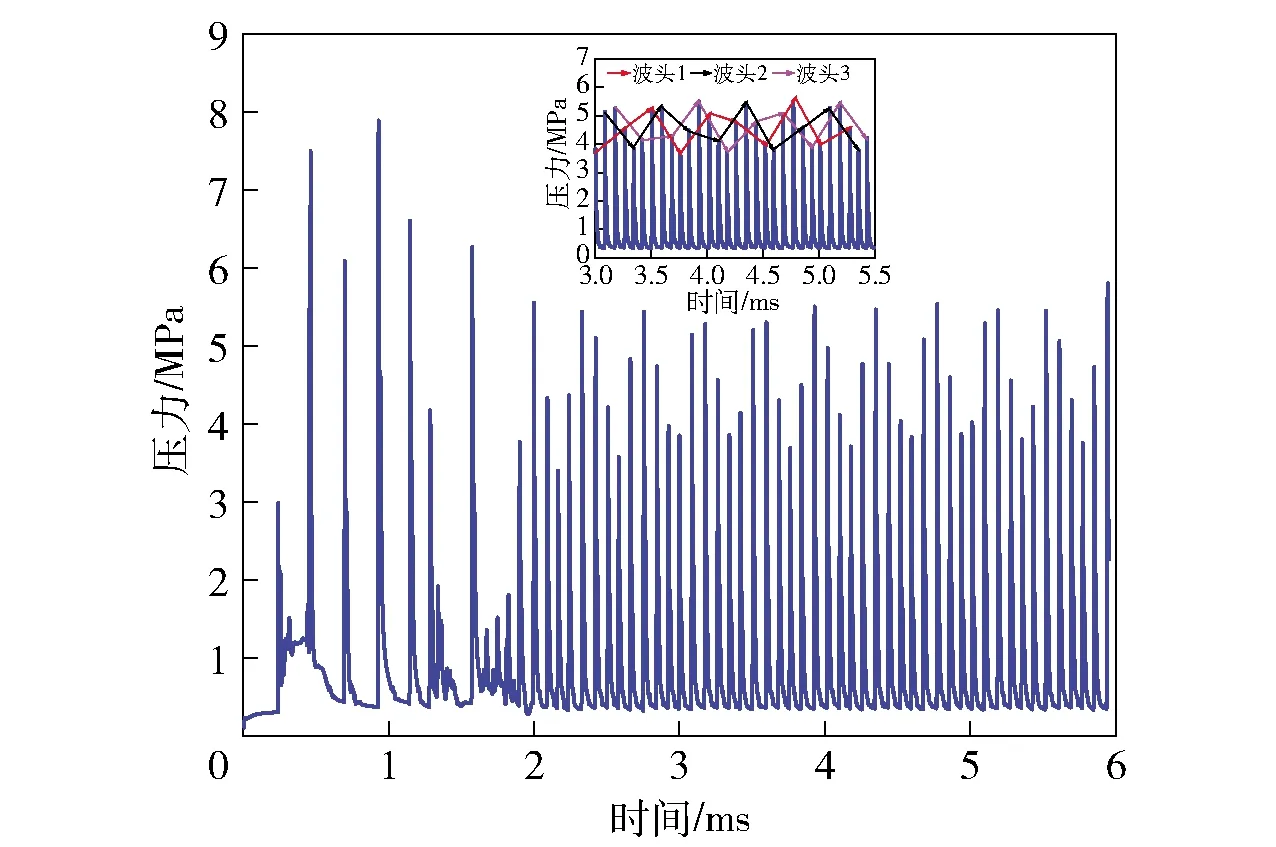
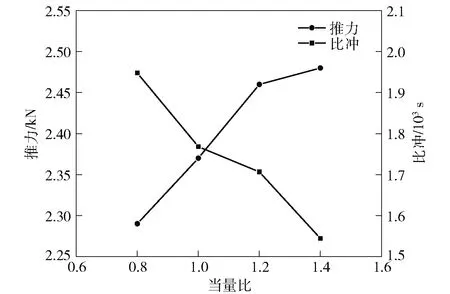
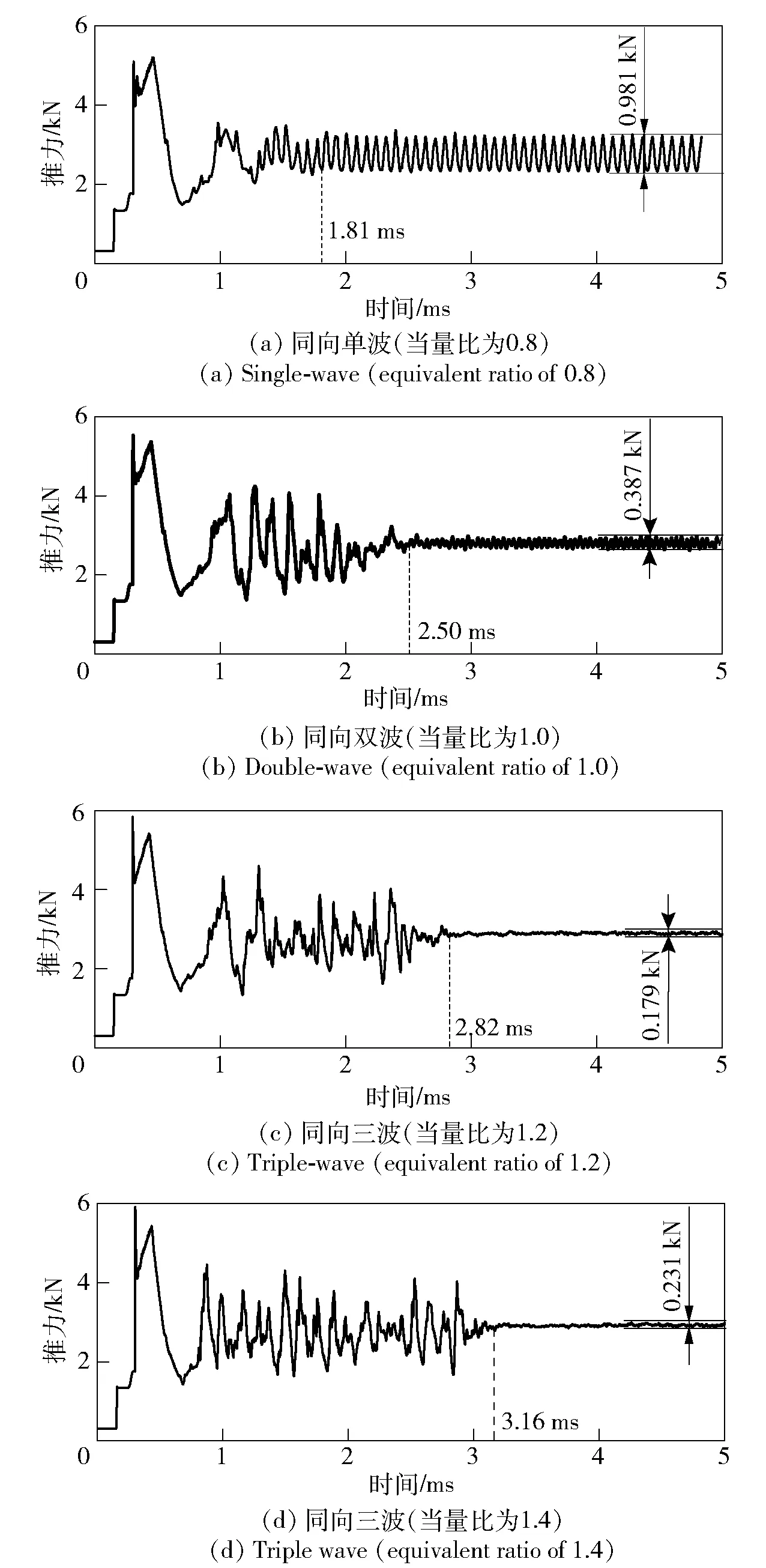
2)若pcr (2) 式中:R为气体常数。 3)若ph (3) 为了模拟真实点火过程,在燃料喷射条件下,通过一股热射流切向喷入燃烧室完成点火过程。如图2所示,初始时计算区域内充满环境大气,计算开始后,先通过入口边界向燃烧室内填充燃料和氧化剂的混合物,当形成可燃预混层后点火程序启动。点火位置位于左边界靠近入口处,高度为0.01 m. 在一个极短的时间内,一股p=20p0、T=20T0和周相速度u=1 200 m/s的热射流从点火位置喷射进入燃烧室,完成点火。 由于两相爆轰包含复杂的两相流动和燃烧过程,液滴微粒的描述采用两流体模型[21-22]。为了简化问题,本文做出以下假设: 1)爆轰过程是二维、无黏的,忽略与壁面的热传导、热辐射和摩擦力的影响; 2)液滴保持球形,温度分布均匀,液滴间互不影响; 3)液滴通过蒸发和剥离变为气态,并且与其他气体瞬间混合均匀。 根据以上假设,得到二维气液两相连续旋转爆轰的控制方程: (4) (5) (6) (7) (8) (9) (10) 式中:φ、ρ、u、v、E分别为体积分数、密度、周向速度、轴向速度和总能,p为气相压力,下标g代表气相参数,下标l代表液相参数;Yk(k=1,2,3,4,5)分别为汽油蒸汽、氧气、二氧化碳、水蒸气和氮气的质量分数;Cv为汽油液滴的定容比热;Id为单位体积的液滴质量变化率[23-24], (11) |vg-vl|=[(ug-ul)2+(vg-vl)2]1/2, (12) (11)式中第1项是液滴的剥离项,第2项是液滴的蒸发项,r为液滴半径,(11)式已在多篇文献中得到验证[21-22],本文所用液滴初始半径为40 μm,N为单位体积内的液滴数,μg和μl分别为气相和液相的黏性系数,vg和vl分别为气相和液相的速度矢量,L为燃料液滴的蒸发潜热,λ为气体的热传导系数,Nu为Nusselt数, Nu=2+0.6Re1/2Pr1/3, (13) Re为雷诺数, (14) Pr为普朗特数;ωkp为每个组分的生成速率;ωkc为每个组分的消耗速率;Qc为汽油蒸气燃烧的释放热;Qd为单位体积内气液两相之间的交换热, Qd=4πr2NλNu(Tg-Tl)/2r; (15) Fx、Fy分别为气体作用于单位体积混合物中液滴的拖拽力[21-22], Fx=0.5Nπr2CDρg|vg-vl|(ug-ul), (16) Fy=0.5Nπr2CDρg|vg-vl|(ug-ul), (17) CD为拖曳力系数, (18) 本文采用辛烷的一步化学反应代替汽油燃烧过程[10-11],这种方法可以较为准确地反映燃烧室内组分的变化过程,并且相比于详细的基元化学反应可以节约大量时间。辛烷液滴经蒸发和剥离后变为气态辛烷参加化学反应,气态辛烷的一步化学反应式为 C8H18+12.5O2+N2→8CO2+9H2O+N2, (19) (19)式中的5个气相组分分别是气态辛烷、氧气、氮气、二氧化碳、水蒸气。根据Arrhenius定律,汽油蒸汽的消耗速率为 (20) 式中:A为化学反应指前因子;n1和n2分别为反应级数;Ea为活化能;R0为通用气体常数。其余组分的质量变化速率可根据该反应公式的当量系数计算得到。 CE/SE方法是一种用于求解双曲型偏微分方程的数值计算方法,尤其适用于求解包含强间断的问题。它将时间和空间统一进行处理,设立SE和CE,保证了计算格式在计算域内满足物理守恒。 根据Chang[12]对时间和空间统一处理的思想,在CE的各个中心上对SE进行泰勒展开,分别计算CE各个边界面上时间- 空间密度矢量的积分通量,通过对(1)式运用高斯定理, 可以得到非结构化三角形网格CE/SE方法的计算格式: (21) (22) (23) (24) (25) (26) (27) 两相爆轰包含了复杂的源项,本文对于源项的处理方法是,将源项和流动控制方程解耦,先冻结源项求解流场参数,然后不考虑流场的影响,采用4阶龙格- 库塔法求解源项,4阶龙格- 库塔法的时间步长取为 (28) 式中:NR-K取为10. 在计算效率方面,对非结构化三角形网格CE/SE方法进行并行化处理。基于直接控制共享内存式并行编程的应用程序接口OpenMP并行化方法设计并行优化方案,将计算程序实现并行化,节省了大量时间。 平面激波反射算例是检验二维算法的一个经典算例。该算例初始时在平面的左上角给定一个与上边界夹角为29°的悬挂斜激波,激波左侧来流参数为ρ=1.0,u=2.9,v=0,p=1/1.4,激波右侧气体参数ρ=1.7,u=2.619 3,v=-0.528 2,p=1.528 2.ρ、u、v、p在此算例中分别是无量纲化的密度,x轴、y轴方向的速度以及压力。左边界、上边界采用来流边界,下边界为固壁边界,右边界为自由出口边界。 本文用于计算激波反射算例的计算区域如图3所示,边界上划分三角形网格边长为2 mm. 该区域共划分为22 722个三角形,计算时间为无量纲时间2.5. 图4给出了使用非结构化三角形网格CE/SE方法计算所得的激波反射云图和等值线图,图5为y=0.5处的压力系数Cp分布图和精确解的对比,Cp=2(p/p∞-1)/(γMa2),p∞为大气压力,此处设置为0.1 MPa,Ma为马赫数。从图5可以看出,稳定后的入射和反射激波具有较高的分辨率,压力系数基本与精确解吻合,证明了该方法在使用2 mm三角形网格时具有准确捕捉激波的能力。 图3 非结构化三角形网格Fig.3 Unstructured triangular meshes 图4 压力系数Cp云图和线图Fig.4 Contour and line graph of Cp 图5 中线y=0.1 m上压力系数分布Fig.5 Distribution of Cp for y=0.1 m 采用非结构化CE/SE方法对气液两相RDE燃烧室内流场进行了数值计算,研究进气总压和当量比对两相RDW的影响,分析不同模态RDE的工作特性。 进气总压对RDW的传播过程具有较大的影响。在恰当量比下,分别计算了进气总压为0.5 MPa、0.6 MPa、0.7 MPa、0.8 MPa时两相RDW的传播特性,如表1所示。 在计算RDE的总推力时,采用火箭式发动机公式,静推力即等于总推力,燃烧室推力为 (29) 式中:ρ、v、po分别为出口处的燃气密度、速度和压力。此时基于燃料的比冲Isp为 (30) 表1 RDE各参量随进气总压变化统计表Tab.1 Parameters of RDE with the increase in total inlet pressure (31) 为了计算推力等参数,假设计算模型有一个0.01 m的厚度,即本文所求推力、比冲等参量,均是基于燃烧室厚度为0.01 m、头部周长为0.3 m的RDE模型。在改变进气总压条件下,各算例获得稳定传播的爆轰波时间各不相同,但最终均形成了稳定的RDW. 在各算例燃烧室内流场进入稳定传播阶段后,选取离散的若干时刻来计算流场的推进性能物理量,最后以各时刻的平均值作为最后的结果。 计算所得RDE传播特性如表1所示,爆轰压力选取20周内RDW的波动范围。在当量比为1的条件下,仅在进气总压为0.5 MPa时燃烧室内形成了稳定传播的同向双波RDW,如图6所示。其余各算例均形成了同向三波RDW. 在此仅给出进气压力为0.6 MPa时同向三波模态RBW,如图7所示。图7中的三波模态RBW不稳定性较高,每个波头的强度和速度不同,因此也导致每2个波头之间的间隔不一致,但3个波头仍然可以保持动态平衡和自持传播。对比同向双波和同向三波,三波模态的进气压力要高于双波模态,但是双波模态的波头高度仍然明显高于三波模态。 图6 同向双波RDWFig.6 Double-wave RDW 图7 同向三波RDWFig.7 Triple-wave RDW (32) 从表1中波速标准差可以看出,传播速度的不稳定性与爆轰波压力波动的不稳定性一致,即爆轰波的压力波动越大,其传播速度的波动也越大。 郑权等[6]通过试验测量所得汽油与富氧空气RDW传播波速为1 022.2~1 171.8 m/s,通过数值计算所得气两相RDW传播速度为1 204.01~1 265.82 m/s,与试验结果较为接近,爆轰波压力和温度峰值耦合,流场结构与Bykovskii通过数据补偿法监测到的两相旋转爆轰流场结构[2]定性一致(见图1),计算结果与试验研究结果吻合较好。 为了研究当量比对RDW的影响,在进气总压为0.5 MPa条件下,分别计算当量比为0.8、1.0、1.2、1.4共4种情况下RDW的传播特性。计算所得RDE性能参数随当量比变化如表2所示。 表2 RDE各参量随当量比变化统计表Tab.2 Parameters of RDE with increase in equivalent ratio 随着当量比的增加,燃烧室内形成了不同模态的RDW,在当量比为0.8时获得了同向单波模态的RDW,逐步提高当量比,分别在当量比为1.0时形成了同向双波模态RDW,在当量比为1.2和1.4时均形成了同向三波模态RDW. 由此可见,当量比对RDW的波头数影响较大,当量比越低越容易形成单波模态,当量比越高、越容易产生多个波头。随着当量比的提升,多波头模态的压力峰值波动范围也逐渐扩大,表明多波头模态每个波头的强度并不均匀,其强度仍处于动态变化中。对比单波、双波和三波的波速可以发现,随着当量比的提高,爆轰波的波速略有提升,但是,单波模态所形成的爆轰波速度略高于双波和三波。 图8为当量比为0.8时所获得的同向单波模态监测点(0.001,0.001)处压力和温度曲线图。由图8可见,监测点处温度和压力规律波动,表明发动机处于稳定工作中。压力峰值约为5.4 MPa,温度峰值约为2 500 K,二者的上升沿非常陡峭并且紧密耦合在一起,温度峰值到达时间略延迟于压力峰值到达时间,二者的差距在10%以内,符合液态燃料爆轰的典型特征。 图8 单波模态监测点处压力和温度Fig.8 Pressure and temperature of single wave at the monitoring point 图9为当量比为0.8时所获得的单波模态RDW. 由于气液两相RDW传播速度较慢,进气速度对燃烧室流场结构的影响也更为显著。由图9(a)中可见斜激波角度较小,几乎与爆轰波平行。在斜激波作用下,经过斜激波的燃气周向速度方向发生了突跃变化,在斜激波下游和爆轰波上端产生一个涡,将爆轰波上端部分燃气卷入其下游。同时由于气相密度远低于液相,卷入斜激波下游的燃气大部分为未燃空气(见图9(c)),由于缺少燃料热能的释放,导致此处温度较低,即为图9(b)中的爆轰波上端温度较低区域。 图9 单波模态RDWFig.9 Single wave RDW 图10为沿直线y=0.01 m处压力、温度和燃料液滴半径的分布图,由图10可见,压力峰值和温度峰值之间存在2.4 cm的距离,燃料液滴半径在温度峰值处仍有21 μm. 图11为Liu等[7]使用二维5阶WENO方法获得的H2/Air单波模态RDW燃烧室头部周向压力和温度分布曲线。由图11可见,气态燃料爆轰波的压力峰值和温度峰值之间的距离极小,二者完全耦合在一起,燃料燃烧释放的热量可直接支持旋转爆轰波的传播。对比图10和图11可以发现,液滴的蒸发和剥离过程延缓了液滴燃料的燃烧和热量的释放,导致了两相爆轰波温度峰值滞后压力峰值2.4 cm,大量燃料燃烧释放的热量需要穿透2.4 cm的液滴层才得以支撑前导激波的传播,因此温度峰值和压力峰值的不完全耦合也降低了两相爆轰波的传播速度。 图10 压力、温度和液滴半径分布图(y=0.01 m)Fig.10 Distribution graph of pressure, temperature and droplet radius(y=0.01 m) 图11 气态燃料RDW压力和温度分布图[7]Fig.11 Distribution graph of pressure and temperature of gaseous RDW[7] 为了分析不同模态RDW的压力波动特性,将表1和表2中所示压力峰值波动范围绘制成图12. 从图12(a)中可见,随着进气总压的升高,同向三波模态RDW压力波动范围总体呈现出增大的趋势,但是同向双波模态RDW压力峰值波动范围明显低于同向三波模态。图12(b)反映出RDW压力波动范围随当量比增大而增大的趋势,同时也反映出单波模态的压力峰值波动最小,双波居中,三波模态压力波动最大的规律,表明多波头模态虽然可以维持稳定传播,但是每个波头强度并不恒定,爆轰波传播的不稳定性较大。 图12 不同模态RDW压力波动范围图Fig.12 Range of detonation pressure in different modalities 图13给出了进气总压为0.6 MPa时三波模态监测点处的压力曲线。由图13可见,3个爆轰波头的强度并不固定,呈现出规律变化的趋势,每个波头的压力都在高、中、低不断变换。以3.0 ms波头1为例,由于此时波头强度较低,速度落后于波头2,波头前可燃预混层较高,爆轰波得到更多能量的支持,其强度不断增加,逐渐达到顶峰。但在此过程中波头1逐渐接近波头2,其前端可燃预混层变小,爆轰波逐渐减弱,爆轰压力开始降低。3个波头共同维持一个动态平衡,使得三波模态RDW能够持续稳定传播。 图13 三波模态监测点处压力曲线Fig.13 Pressure graph of triple waves at monitoring point 由于RDE通常是一个环形燃烧室,二维数值模拟研究虽然可以反映RDW的传播特性,但是想要深入探究曲率效应和燃烧室宽度对两相旋转爆轰波流场结构和传播不稳定性的影响,后续研究仍然需要进行三维数值仿真以及与试验研究验证的对照。 图14为推力和燃料比冲随当量比变化曲线图。由图14可见:发动机的推力随着当量比提升而提升,但提升幅度较小;发动机比冲随当量比的增加呈现出下降的趋势。 图14 推力和燃料比冲随当量比变化曲线Fig.14 Thrust and specific impulse versus equivalent ratio 图15为按照表2顺序绘制的不同模态RDE推力曲线图。由图15可见,点火之后发动机推力均出现一个突跃的上升,而后迅速降低,经历数次振荡之后逐渐稳定。其中:单波模态进入稳定阶段最快,仅用时1.81 ms;双波模态次之,用时2.50 ms;三波模态最慢,用时2.82 ms和3.16 ms. 进入稳定阶段之后,单波模态发动机推力波动最大,为0.981 kN,是其平均推力的42.84%,双波模态推力波动为0.387 kN,占其平均推力的16.33%,三波模态发动机推力波动最小,为0.179 kN和0.231 kN,是其平均推力的7.28%和9.31%. 因此,多波头模态有利于降低RDE的推力波动,增加RDE的工作稳定。 图15 不同模态推力曲线Fig.15 Thrust graphs of different modalities 本文采用非结构化三角形网格CE/SE方法对气液两相RDW进行了数值模拟,建立了气液两相连续旋转爆轰计算模型,获得了单波模态、同向双波模态以及同向三波模态的气液两相RDW,计算了不同进气总压和不同当量比下的RDW传播过程,分析了不同模态下RDW的压力和推力特性。得出以下主要结论: 1)非结构化CE/SE方法可以准确捕捉激波、爆轰波等强间断,具有良好的应用前景;数值计算所得两相RDW传播波速与试验结果吻合较好,流场结构与试验结果定性一致,验证了数值模拟研究的准确性。 2)液滴的蒸发和剥离过程,延缓了液滴燃料的燃烧,导致两相爆轰波压力峰值和温度峰值的不完全耦合,降低了两相爆轰波的传播速度。 3)当量比对RDW的传播模态影响较大,当量比越低越容易形成单波模态,当量比越高越容易产生多个波头。 4)单波模态的爆轰波压力和传播速度波动最小,双波模态居中,三波模态压力和传播速度波动最大;其推力波动规律与压力波动规律相反,单波模态推力波动最大,双波模态次之,三波模态推力波动最小。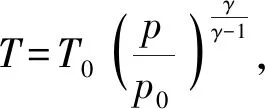
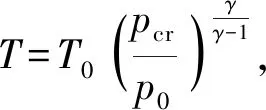
1.2 控制方程
2 计算方法
2.1 CE/SE方法
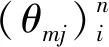
2.2 方法验证
3 计算结果与讨论
3.1 进气总压对两相RDW的影响
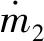
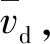
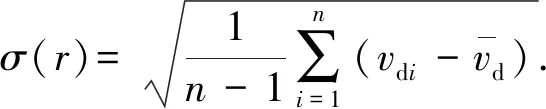
3.2 当量比对两相RDW的影响
3.3 不同模态RDE工作特性分析
4 结论

