基于多通道电感测量的圆周等分孔位置度在线快速评定方法
李兵, 樊寅斌, 孙彬, 兰梦辉, 龙兴元, 侯颖
(1.西安交通大学 机械制造系统工程国家重点实验室, 陕西 西安 710049; 2.西安工业大学 机电工程学院, 陕西 西安 710021;3.秦川机床工具集团股份公司, 陕西 宝鸡 721009)
0 引言
随着科学技术的发展,集精密化、智能化等先进制造技术于一体的工业机器人越来越多地出现在军工和民品生产领域。工业机器人具有精细制造、精密加工等特点,本身高度精密化,具备微米级的加工精度。作为机器人关节RV减速器的核心精密零件,行星架与摆线轮决定了机器人的性能指标,其圆周等分轴孔的位置度对减速器装配精度、载荷分布、传动精度和使用寿命有直接影响[1-2],在加工时必须保证孔组的位置度精度。国内RV减速器尚未形成一套完备的生产体系,成为制约我国RV减速器发展的突出问题。因此,自主研发RV减速器核心零部件的生产加工工艺、在线配套检测装置势在必行[3],其中包括研究开发摆线轮、行星架的位置度在线检测系统。
目前对圆周等分孔位置度的测量与评定主要有综合检具和坐标测量两种方法[4]。综合检具方法是根据实际零件装配情形验证量规能否通过零件,来判断零件合格与否,由于误判率较高,不适用于大批量在线生产过程[5]。坐标测量方法是获取被测件位置坐标信息,通过坐标计算获得孔组位置度,典型代表有三坐标测量机(CMM)和机器视觉测量。CMM通过对测量数据的分离、滤波、拟合、构造,得到被测件的位置度,测量精度高,但效率低,且无法在生产线上直接测量[6-7]。计算机视觉检测技术是一种非接触式测量系统,利用拍摄的数字图像完成对位置信息的获取,得到孔组的位置和方向误差,但受工业相机的分辨率限制,难以兼顾大范围和高精度的要求[8]。
位置度评定是形位公差标准评定中应用最广、难度最大、变化最多的项目之一,评定算法较为复杂,学术界公认的位置度评价必须满足我国国家标准GB/T1958—2017 产品几何技术规范(GPS)_几何公差_检测与验证中规定的最小条件原则[9],而实际测量评定过程中很难实现此要求。目前学术界并未形成一种普适性评价算法,在实际生产中仍需结合零件自身的特点,提出与零件相适应的准确、高效的位置度误差评定方法。
本文通过极角二分法搜索寻优,提出一种基于多通道电感测量的零件圆周等分孔位置度在线快速评定算法,并研制出一种融合位置度量规、坐标测量技术以及多通道电感协同测量技术的位置度在线测量仪,迅速准确得到圆周等分孔最优的位置度误差,并对摆线轮和行星架进行重复性测量实验,对算法进行验证。实验结果表明:算法精度小于1.4 μm,算法可靠;仪器测量重复性误差小于1.5 μm,最大测量误差小于3.0 μm,仪器测量精度较高;单个零件测量节拍小于10 s,适合生产线上的测量要求。
1 测量方案及系统设计
1.1 被测零件分析
位置度指零件被测要素相对于其理想位置所允许的变动量[10],在零件加工过程中,圆周等分孔组不可避免地会出现位置度误差,从而对孔组类零件的加工制造及装配产生重要影响。本文对某型RV减速器320E型摆线轮与行星架位置度测量进行研究。摆线轮圆周等分孔通过轴承与曲柄轴装配,行星架为整个减速器结构的基础,其圆周等分孔需要安装轴承以与其他零件装配[11-12]。圆周等分孔位置度直接影响减速器运行中的载荷分布、传动平稳性,进而影响减速器寿命,因此必须保证较高的加工精度。摆线轮与行星架零件图如图1所示。

图1 摆线轮与行星架Fig.1 Cycloid gear and planet carrier
精密测量在选择测量基准时应该遵循基准一致的原则,测量基准应与零件设计基准和加工基准一致[13]。孔组的位置度公差为被测要素轴线与理想轴线所形成的圆柱形公差带,通过公差带φT限制孔的实际轴线[14],T为理想公差值。以摆线轮为例,其位置度要求为0.008 mm. 圆周孔组位置度公差如图2所示,其中f1~f3表示各孔的位置度误差。

图2 摆线轮公差图Fig.2 Tolerance diagram of cycloid gear
1.2 测量原理分析
本文提出一种融合位置度量规、坐标测量技术以及多通道电感协同测量技术的圆周等分孔测量方法。在被测圆周等分孔和基准的同一水平截面分别对径布置4个电感传感器,总共16个传感器,测量传感器形成的坐标系与零件设计坐标系一致。传感器安装在测量导向套筒内,测量导向套筒根据位置度量规的测量原理进行设计,测量时导向套筒与被测孔配合。由于摆线轮和行星架圆周等分孔的设计基准不同,行星架以大外圆作为圆周孔的加工基准,摆线轮以中心孔作为加工基准。针对行星架和摆线轮设计的不同传感器布置方式如图3所示。

图3 传感器布置图Fig.3 Sensor layout
采用静态比较测量方式,位置度误差测量的实质是通过电感传感器测量被测件孔心相对于标准值的变化量。在对被测件进行检测之前,先对传感器进行标准件标定,以已知高精度合格零件作为标准件,获得标准件传感器示值,每批被测零件共用同一标准件信息。标定过程和测量过程相同,测量时生产线上的机械手将工件放置在测量工位,采样被测件每个传感器的数据,得到每个传感器相对于标准件的变化量w1,w2,…,w16. 通过传感器值的变化量,拟合被测孔心坐标变化。如图4所示,以摆线轮基准孔为例,可以计算得到基准孔孔心(x0,y0)相对于标准件基准孔孔心(X0,Y0)在x轴、y轴上的变动量Δx0、Δy0,同理可得到圆周各孔孔心相对于标准件的变动量Δxi、Δyi:
(1)

图4 孔心变动示意图Fig.4 Schematic diagram of hole coordinate change
标准件孔心坐标由瑞典海克斯康公司产Leitz Infinity15.9.7/B4s CMM提供,其位置测量时综合精度误差值可达1.3 μm/1.0 m,得到的标准件孔心坐标值真实可信。作为本测量方法中对比的标准量,标准件基准中心及圆周等分Ⅰ、Ⅱ、Ⅲ孔心的三坐标机测量值记为O(X0,Y0)、A(X1,Y1)、B(X2,Y2)、C(X3,Y3)。记被测件各孔的各孔心坐标O(x0,y0)、A(x1,y1)、B(x2,y2)、C(x3,y3),得到被测量相对标准件的孔心变化量后,根据(2)式即可求得被测零件各个孔的孔心坐标值:
(2)
式中:i=1,2,3.
本文所设计的圆周等分孔测量方法结合了比较式测量法和坐标测量法的优点,通过多通道电感采集零件被测孔的坐标数据,对比标准件数据,得到被测零件的各等分孔孔心坐标值。然后通过本文第2节的极角二分法搜索寻优算法,迅速准确地得到各等分孔满足最小条件原则的最优位置度误差。
1.3 测量系统设计
为适应自动化生产线车间的环境要求,位置度在线测量仪由大理石工作台、位置度测量部、传感器信号调理电箱、数据采集卡、工控机等组成。结合计算机技术完成评定算法,实现在线高精度快速测量。
位置度测量部由导向套筒、安装基板、电感传感器、保护罩壳等组成。行星架位置度测量部和摆线轮位置度测量部分别如图5(a)和图5(b)所示。

图5 位置度测量部Fig.5 Measurement modules
为便于测量过程中工件的顺利取放,结合位置度量规原理,设计相应导向套筒,防止传感器受到较大的撞击,将传感器安装在导向部件中,再将导向套筒按零件上各孔之间的相对位置与基板进行精密装配。导向装置的装配结构如图6所示。
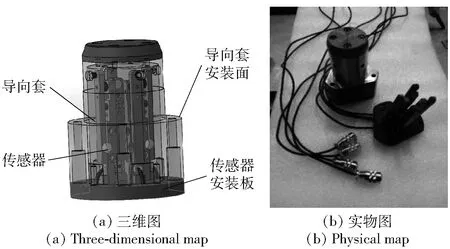
图6 导向装置Fig.6 Guiding device
系统的数据采集模块是实现位置度在线测量的技术关键。数据采集系统主要完成电感传感器的信号采集,通过高精度处理电路,将位移信号转换成电信号,通过端子板与基于总线PCI-1317的数据采集卡进行模拟信号与数字信号转换,完成系统的数据采集,经过滤波放大后传送给工控机,参与到零件测量的计算。在VC集成开发环境下,基于MFC类库对开发基于对话框程序界面,实现人机界面设计,通过相应的协议和算法实现工控机与硬件设备的实时通讯,实现在线自动化检测功能。
2 位置度算法原理
本文基于极角二分法搜索寻优,利用多通道电感传感器采集的被测孔孔心坐标,利用算法进行处理,在圆周等分孔在切向偏移方向不确定的情况下,无需进行切向基准选择,迅速准确得到各等分孔满足最小条件原则的最优的位置度误差。具体算法原理如图7所示。图7中,M为位置度公差,R为定位圆半径,ri为圆周各孔与基准孔之间的孔心距。

图7 位置度评定算法流程图Fig.7 Flow chart of position degree evaluation algorithm
2.1 位置度误差评价数学模型的建立
设H为零件各圆周等分孔理论坐标点构成的集合,S为孔组各实测坐标点构成的集合。根据定义,位置度误差f应为集合H中各坐标点到集合S中相应点距离的2倍(见图8):
f=2|sh|,
(3)
式中:s∈S;h∈H.
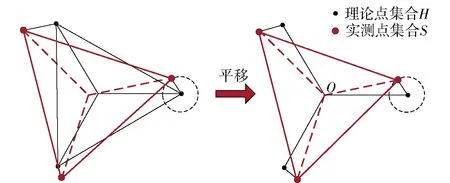
图8 位置度误差模型Fig.8 Error model of position degree
在得到被测圆周等分孔各孔的坐标值后,由孔心组成的孔心多边形旋转一定的角度范围时,存在实测坐标点逼近理论点的旋转角度,以此可搜索各实际测量坐标点的最优位置,使位置度满足最小条件原则[15]。设S旋转处理后的零件各提取要素的实测坐标点构成集合Q,此时孔组位置度误差与Q的元素有关,可以得到一个位置度误差集合。当位置度误差集合中各元素的最大值最小时,符合最小条件原则,因此可建立位置度误差模型F(Q):

(4)
2.2 被测孔关键参数求解
为实现检验基准和设计基准的统一,将实际等分孔即孔心多边形平移,使基准孔孔心o(x0,y0)与理想定位基准中心O(X0,Y0)重合,并求解各孔心平移后的等分孔孔心坐标Ⅰ(x′1,y′1)、Ⅱ(x′2,y′2)、Ⅲ(x′3,y′3)(见图9):
(5)
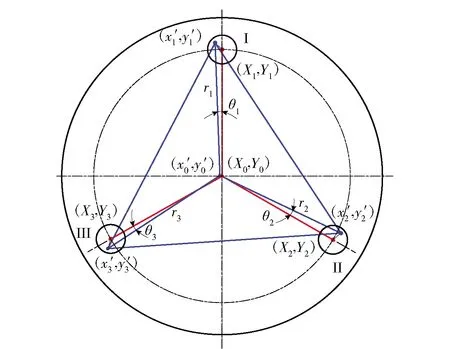
图9 孔心多边形变换图Fig.9 Transformation diagram of hole center polygon
根据平移后的坐标信息,可得
(6)
(7)
计算i孔实际孔心坐标相对于i孔理想孔心的偏移距离m(即i孔初始位置度的一半),然后计算i孔实际孔心线和理想孔心线的极角差θ.
各实际孔心偏移距离和极角差计算为
(8)
(9)
当实际孔心在理想孔心顺时针方向时,θi取正值,否则取负值。
2.3 孔心多边形旋转处理
判别各孔位置度是否满足公差要求,如果|ri-R|>M/2,则该零件等分孔的位置度肯定已经超差,判定该零件不合格,无需再进行精度测量。
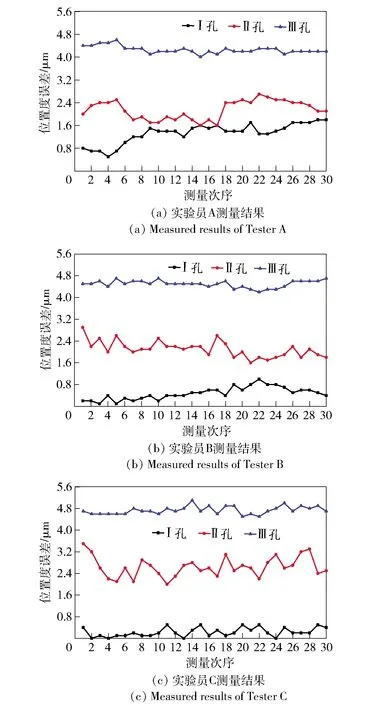
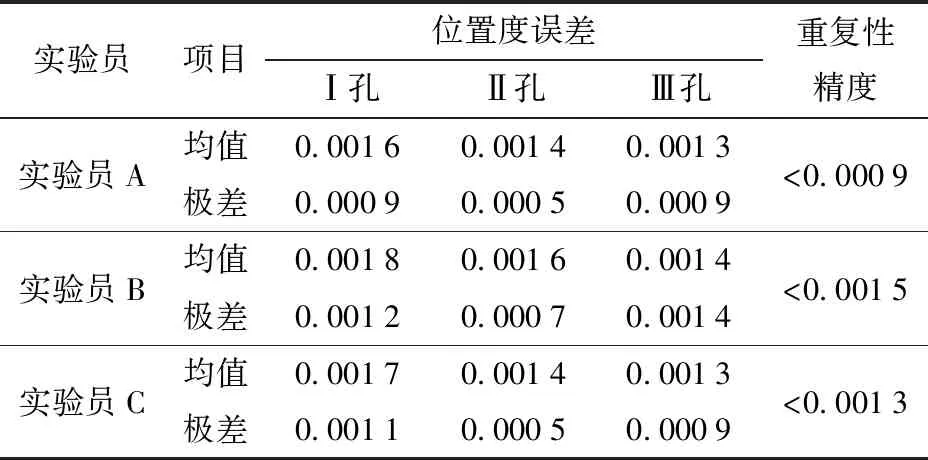
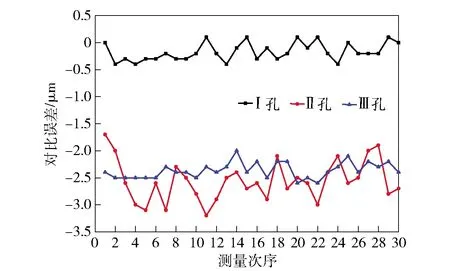
如果|ri-R| 图10 孔心多边形旋转图Fig.10 Rotation diagram of hole center polygon 由几何关系,有 (10) 当顺时针旋转时,取“+”号,当逆时针旋转时,取“-”号;因此,极角差θi在满足位置度误差要求前提下可以旋转的角度满足 (11) 当孔心多边形顺时针旋转时, (12) 当孔心多边形逆时针旋转时, (13) 在得到每个等分孔满足位置度误差要求的顺时针和逆时针旋转角度β1,β2,β3和β′1,β′2,β′3后,分别取交集,得到孔心多边形整体满足位置度误差要求的可旋转最大角度范围βmax、β′max. 确定孔心多边形整体满足位置度误差要求的可旋转角度范围后,开始第k次位置度二分法搜索寻优。 顺时针旋转不同角度得到各孔的位置度误差为 (14) (15) (16) (17) (18) (19) 由此前分析可知,零件孔组的误差模型F(Q)是在最小条件原则基础上建立的。将F(Q)求解步骤进行分解,首先令一个集合W(Q0): W(Q0)∈F(Q), (20) (21) W(Q0)是对5组不同旋转角度多对应的3个孔位置度误差值中的最大值组成的一个位置度误差值集合: 在集合W(Q0)的元素中,找出数值最小的元素w′(k): w′(k)=minW(Q0). (22) 同理可求得逆时针旋转时的最优位置度误差{f′1、f′2、f′3},比较顺时针旋转和逆时针旋转得到的结果,确定最优的1组位置度误差。 随着迭代搜索寻优次数的增加,各孔位置度误差值会逐渐收敛,愈发逼近位置度误差的最优解。收敛条件取决于算法评定精度的要求,本文位置度误差评定算法的精度设置为0.000 1 mm,即第k+1次得到的每孔位置度与第k次得到的相应孔位置度的差值小于0.000 1 mm,因此本文算法的终止条件为 (23) 本文所研制的位置度在线测量仪面向零件自动化生产线,存在电磁干扰、温度漂移及灰尘油污等多种影响测量精度的因素,同时测量部机械结构与装配精度也不可避免地会给系统引入误差。综合分析可知,位置度测量仪的误差源主要有系统误差、随机误差和粗大误差。系统的主要误差源分解如图11所示。 图11 系统误差分析Fig.11 Systematic error analysis 本文重点对测量精度影响较大、较易分离的误差进行分析和补偿,着重对检测系统自身的主要误差源即传感器非线性误差进行分析和补偿,以减小最终检测结果的偏差。 位置度测量仪误差来源较复杂,系统误差主要包括传感器安装误差、传感器非线性误差和测量部装配误差等,其中传感器安装误差和测量部装配误差是由于制造和装配不完善引起的,可通过精密装配和调试来降低,同时本测量仪的比较式测量方法可基本消除测量仪几何误差带来的测量误差。随机误差是生产线上环境因素引起的误差,主要包括温度漂移、振动噪声和电磁干扰等。由于被测零件是孔型零件,温度变化会引起零件孔变形,进而影响测量。本文测量仪使用场所为陕西秦川机床工具集团有限公司恒温车间,温度恒定在(20±1) ℃范围内,因此温度给测量实验带来的误差很小。同时由于本文测量方法是比较测量,当温度变化过大时,可在同温度下对测量仪重新标定,以规避温度变化对测量精度的影响。针对振动噪声和电磁干扰,本文通过优化测量仪机械结构和增加软件滤波的方式降低影响。粗大误差主要是由操作不当、电压突变和仪器故障等引起的,规范操作和前期设备检查可有效避免。 选用差动式杠杆电感位移传感器,在生产车间环境下,采用三门峡中原量仪股份有限公司生产的BCT-5C型微动测量台架,配合标准量块和数据采集电箱,进行传感器的静态标定实验,如图12所示。测量原理是旋动右侧千分螺旋头,旋转1周时微动块横向移动 0.5 mm,纵向升高 0.01 mm,测量精度达0.2 μm. 在传感器测量范围为-50~50 μm的线性段,将传感器初始示值调为0,旋动千分螺旋头,使量块向右运动,每向右运动0.25 mm,便记录相应传感器的示值,再调0从0向左运动,每0.25 mm记录1个传感器示值,共记录21个数据。重复进行5次实验,对5组数据进行处理,求取平均值,并与标准数值作差,得到传感器非线性误差散点数据,如表1所示。 图12 传感器标定实验Fig.12 Sensor calibration experiment 表1 传感器非线性误差实验结果 标定次序理想位移实际位移非线性误差标定次序理想位移实际位移非线性误差1-50-47.862.141255.300.302-45-44.160.84131010.220.223-40-39.460.54141515.110.114-35-34.880.12152019.90-0.105-30-30.000162524.73-0.276-25-24.900.08173029.70-0.307-20-19.920.08183534.71-0.298-15-14.900.10194039.26-0.749-10-10.28-0.28204544.15-0.8510-5-4.810.19215048.38-1.62110-0.08-0.08 采用最小二乘法,对实验所得的传感器非线性误差数据(xv,yv)进行曲线拟合,其中v=0,1,2,…,n-1,xv表示理想位移,yv表示非线性误差,使实验数据与拟合曲线各离散点上偏差的平方和趋向于最小值,求取误差的曲线方程。 使用一个p次多项式σ(x)来拟合v个误差数据点(xv,yv),求取被测点的逼近函数,确定多项式系数av以及多项式次数q: (24) 选用4~7次多项式对误差进行逼近,结合残差平方和与相关系数,选取6次多项式作为误差逼近的多项式,求出非线性误差的静态标定拟合曲线的表达式。通过将测量中传感器示值y(xv)与相应离散点上误差函数的值进行叠加,得到传感器的非线性误差补偿修正值Y(xv): Y(xv)=y(xv)-σ(x). (25) 补偿后的数据绘成折线图,如图13所示。由图13可见,测量范围边缘从2.0 μm降至0.5 μm以内,整体非线性误差小于0.5 μm,传感器输入输出的线性关系得到明显改善,测量系统精度得到了较大提升。 图13 传感器非线性误差补偿结果Fig.13 Compensation result of sensor nonlinear error 为了验证二分法搜索寻优算法的正确性和精确度,进行算法仿真实验,其原理是使用精度较高的CMM对零件样品进行相关参数测量,测得零件各孔孔心的坐标值、位置度误差值。将各孔孔心的坐标值代入算法得到搜索寻优结果,并与三坐标测量结果进行对比。 本文实验在VS开发环境下实现上述位置度算法,对CMM测得的孔心坐标数据进行相应算法处理,得到位置度算法仿真结果如表2所示。 表2 位置度算法仿真结果Tab.2 Algorithm simulation results of position degree 从表2可以看出,本文评定算法得到的位置度误差值与三坐标测量值之间的误差较小,对于零件编号为Z1412187的摆线轮位置度误差评定精度小于1.0 μm,零件编号为1504124的行星架位置度误差评定精度能保持在1.4 μm以内,证明了本文算法的正确性和精确度。 在进行测量实验时,从上料到完成测量,单个零件测量节拍<10 s,可实现对行星架和摆线轮圆周等分孔组位置度在线快速测量,满足工业机器人RV减速器生产线上检测的要求。实验场所位于陕西秦川机床工具集团有限公司成套设备车间,与实际生产线环境相吻合,满足验证实验要求。 在相同实验条件下,对零件编号为Z1807055的摆线轮零件和零件编号为1809122的行星架进行测量实验,每次测量由1位测量员对所有样品进行一轮测量。为验证测量仪的再现性和重复性,共由3位不同的实验员进行实验,每个零件每次进行30次重复测量实验,将测量结果绘制成折线图,以不同线型表示不同孔的位置度误差。 图14(a)、图14(b)和图14(c)为不同实验员测量得到的编号为Z1807055的摆线轮各孔位置度结果。 图14 编号为Z1807055的摆线轮孔组位置度误差Fig.14 Hole group position of cycloid gear Z1807055 分析图14(a)、图14(b)、图14(c)数据计算可知,不同实验员测得编号为Z1807055的摆线轮圆周Ⅰ、Ⅱ、Ⅲ孔位置度均值和极差如表3所示,测量重复性精度<1.3 μm,再现性分别为1.0 μm、0.5 μm、0.5 μm,小于1.0 μm. 同理可得到编号为1809122的行星架位置度测量结果,如图15所示。 表3 编号为Z1807055的摆线轮实验结果分析Tab.3 Analysis of experimental results of cycloid gear Z1807055 mm 图15 编号为1809122的行星架孔组位置度误差Fig.15 Hole group position of planet carrier 1809122 分析图15可知,不同实验员测得编号为1809122的行星架圆周Ⅰ、Ⅱ、Ⅲ孔位置度均值和极差如表4所示,测量重复性精度<1.5 μm,再现性分别为0.2 μm、0.3 μm、0.1 μm,小于0.3 μm. 表4 编号为1809122的行星架实验结果分析Tab.4 Analysis of experimental results of cycloid 1809122 mm 综上所述,实验结果满足RV减速器自动生产线对测量仪的测量重复性精度和再现性要求,证明了该位置度检测装置和评定算法的可靠性。 使用CMM对实验对象的位置度误差进行测量,通过分析本文测量仪测量值与三坐标测量值之间的关系,对测量系统的准确度进行验证。本文使用瑞典海克斯康公司生产的Leitz Infinity 15.9.7/B4s型CMM对Z1807055摆线轮和1809022行星架圆周孔进行测量,获得三坐标机测量值。通过大量实验数据显示实验员C操作测量仪比较熟练,获得的数据更真实稳定。因此,选取实验员C的测量数据作为本文精度验证实验数据,将每次测量结果与三坐标测量结果作差,其中Z1807055摆线轮圆周Ⅰ、Ⅱ、Ⅲ孔三坐标测量值分别为0.000 4 mm、0.005 2 mm、0.007 1 mm;1809022行星架圆周Ⅰ、Ⅱ、Ⅲ孔三坐标测量值分别为0.003 6 mm、0.003 7 mm、0.001 8 mm;得到各孔测量对比误差值,如图16、图17所示。 图16 Z1807055摆线轮对比误差Fig.16 Contrast errors of cycloid gear Z1807055 图17 1809122行星架对比误差Fig.17 Contrast errors of planet carrier Z809122 分析图16、图17可知,摆线轮和行星架测量仪相对于CMM对比误差的均值和极值如表5所示,摆线轮Ⅰ孔的对比误差平均小于0.17 μm,Ⅱ孔对比误差平均小于2.56 μm,Ⅲ孔对比误差平均小于2.37 μm;行星架Ⅰ孔的对比误差平均小于1.95 μm,Ⅱ孔对比误差小于2.26 μm,Ⅲ孔对比误差小于0.4 μm;同时测量仪的对比误差极值小于3 μm,测量精度和准确性较高。 表5 位置度误差对比实验结果Tab.5 Comparative experimental results mm 本文针对在线测量RV减速器精密零件行星架与摆线轮的圆周等分孔位置度问题,提出一种基于多通道电感测量的零件圆周等分孔位置度在线快速评定算法,并研制出位置度在线测量仪。通过理论分析与实验验证,得出以下结论: 1)研制出一种融合位置度量规、坐标测量技术以及多通道电感协同测量技术的摆线轮行星架位置度圆周等分孔在线测量仪,操作简便,单个零件测量节拍小于10 s,适合生产线上的测量要求。 2)利用多通道电感传感器采集零件被测孔的坐标数据,提出一种极角二分法搜索寻优算法,在圆周等分孔在切向偏移方向不确定的情况下,无需进行切向基准选择,迅速准确得到各等分孔满足最小条件原则的最优位置度误差。 3)算法仿真实验结果表明,算法精度小于1.4 μm,接近三坐标测量精度,算法精度高;重复性实验结果表明,摆线轮测量部的重复性精度小于1.3 μm,再现性小于1 μm. 行星架测量部重复性精度小于1.5 μm,再现性小于0.3 μm,证明了该位置度评定算法和仪器的稳定性和可靠性;精度对比实验结果表明,测量仪与三坐标机对比误差平均小于2.6 μm,验证了本文研制的测量仪具有较高的测量精度。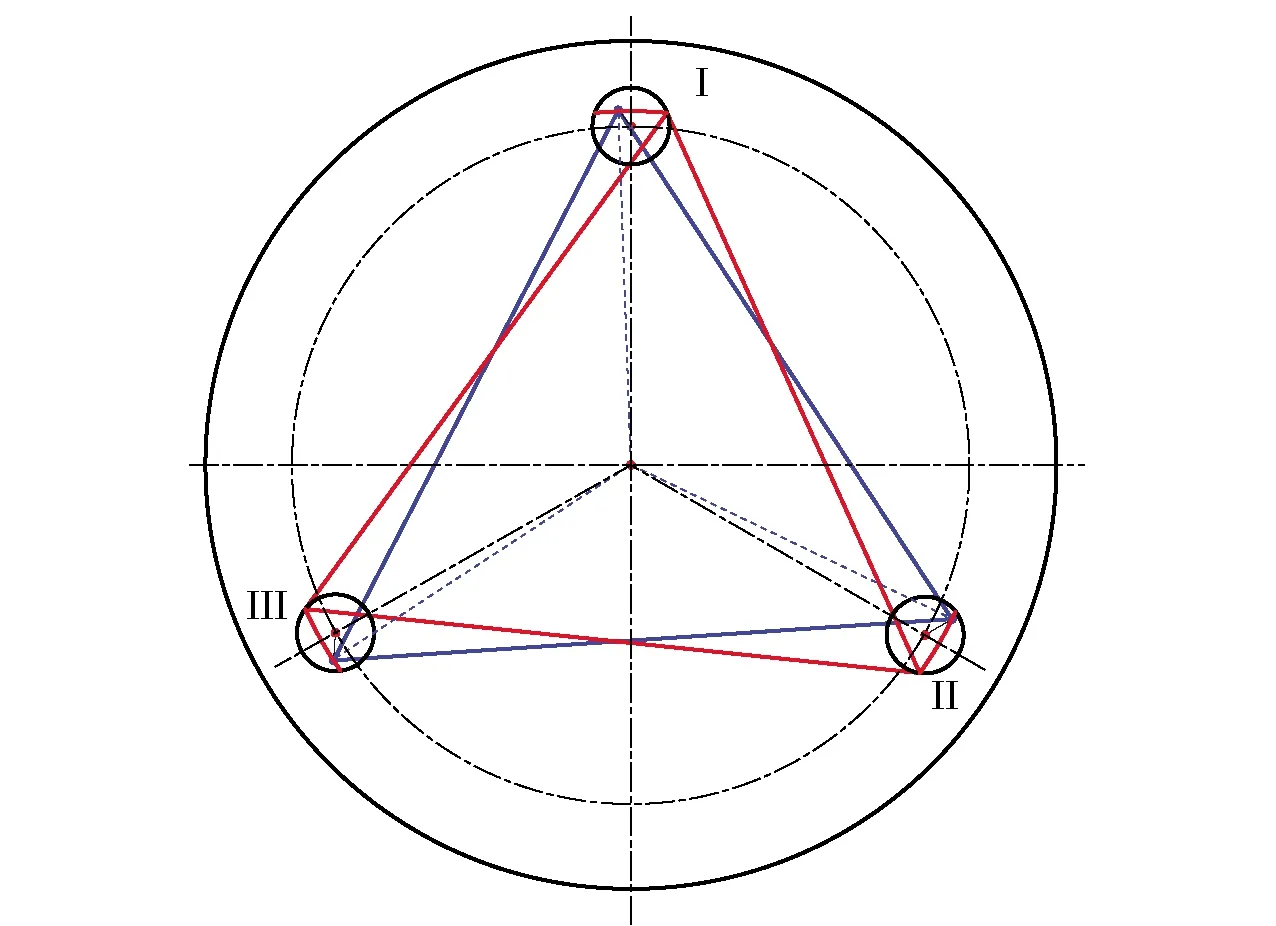
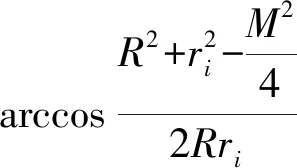
2.4 二分法迭代搜索寻优
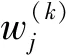
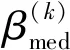
2.5 迭代终止条件
3 误差分析与补偿

3.1 总体误差分析
3.2 传感器静态标定实验

Tab.1 Experimental results of sensor nonlinear errors μm
3.3 传感器非线性误差建模与补偿

4 测量实验
4.1 算法仿真实验

4.2 重复性测量实验


4.3 精度验证实验


5 结论

