微凹坑超声电解滚蚀加工间隙多物理场特性及成形规律

王明环， 王嘉杰， 童文俊， 陈侠， 许雪峰， 王芯蒂

(1.浙江工业大学 机械工程学院， 浙江 杭州 310014; 2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室， 浙江 杭州 310014)

0 引言

理论研究和工程实践都已证明，具有一定表面粗糙度或纹理的摩擦副表面比光滑表面更有利于润滑膜的形成，进而减小摩擦力并降低摩擦磨损[1-2]。表面微织构可应用于航空航天、电子、汽车等工业领域，如航空引擎的冷却空气管和阻尼衬套、电子显微镜的光栅和活塞表面纹理等[3-5]。微细电解加工具有加工效率高、表面质量好、工具无损耗、无切削应力及不受材料力学性能影响等优点，在金属表面微细加工领域发挥了重要作用[6-7]。但在微细电解加工过程中，间隙流场的复杂性和随机性导致加工尺寸可控性与加工稳定性差[8]。

为了提高电化学加工的定域性，减少杂散腐蚀的影响，国内外研究人员对电解加工的间隙能场进行了研究，并提出一系列改善加工精度的方法。王明环等[9]以螺旋深小孔电解加工为研究对象，基于数值模拟揭示了电解加工间隙流场特性。Wang等[10]提出气膜屏蔽电解加工方法，通过数值仿真对材料腐蚀过程中的多物理场变化进行了分析。

超声能场辅助电解加工是一种有效的提高材料成形精度的方法，众多学者基于超声复合电解加工，取得了一定的研究进展。Ruszaj 等[11]发现工具阴极的超声振动可有效改善工件表面加工质量。Wang等[12]通过控制盘状工具阴极作轴向超声振动，有效促进了大深径比电解加工中间隙产物的排出，加工出深5.4 mm、深径比12.3的微小孔。Hewidy等[13]研究了低频振动电解加工，发现低频振动改变了加工间隙物理状态，能有效提高加工精度与表面质量。Bhattacharyya等[14]研究了超声振动频率对加工精度、材料去除率的影响，从间隙产物去除的角度解释了超声对电解加工的影响。文献[15-17]基于一系列试验对超声复合电解加工进行基础性研究，通过对材料钝化层的分析，发现超声复合电解加工能有效消除电解钝化。赵志强[18]通过数值仿真，从空化泡角度进行分析，研究了超声产生的空化作用对间隙流场参数的影响。

以往工艺及理论研究表明了超声能场在改善工件加工质量上的作用。然而，在超声能场下，微细电解加工间隙能场变得异常复杂，加工间隙可观性较差，材料去除规律难以把握。通过数值仿真，能方便地进一步探究超声对于微细电解加工的影响。

本文基于超声能场对微细电解加工性能提高的优势以及工程上对群微织构加工需求，提出径向超声能场滚蚀微细电解加工(RUR-EMM)方法，对超声能场作用下间隙耦合场变化对微凹坑成形的影响进行研究。通过建立加工过程中间隙多物理场耦合模型，利用数值分析方法得到径向超声能场对于微细电解加工间隙耦合场的影响规律。对比研究了滚蚀微细电解加工(R-EMM)与RUR-EMM间隙内两相流场、电场、温度场的分布规律，并通过工艺试验对微凹坑成形仿真结果进行了验证。

1 RUR-EMM原理

RUR-EMM原理如图1所示，表面带有微凸台结构的径向超声换能器(工具阴极)接电源负极，绕固定轴以一定角速度ω旋转；阳极工件接电源正极，以一定线速度v平移，二者作相对运动。加工时超声换能器表面的阵列微凸台以速度vr作径向振动，在接通加工电源、电解液为导电介质下，阳极工件表面材料得到蚀除形成凹坑。

阴阳两极电化学反应为

N-ne-→Nn+，

(1)

2H++2e-→H2↑，

(2)

式中：N为工件材料；n为电子数；Nn+为工件材料离子态。

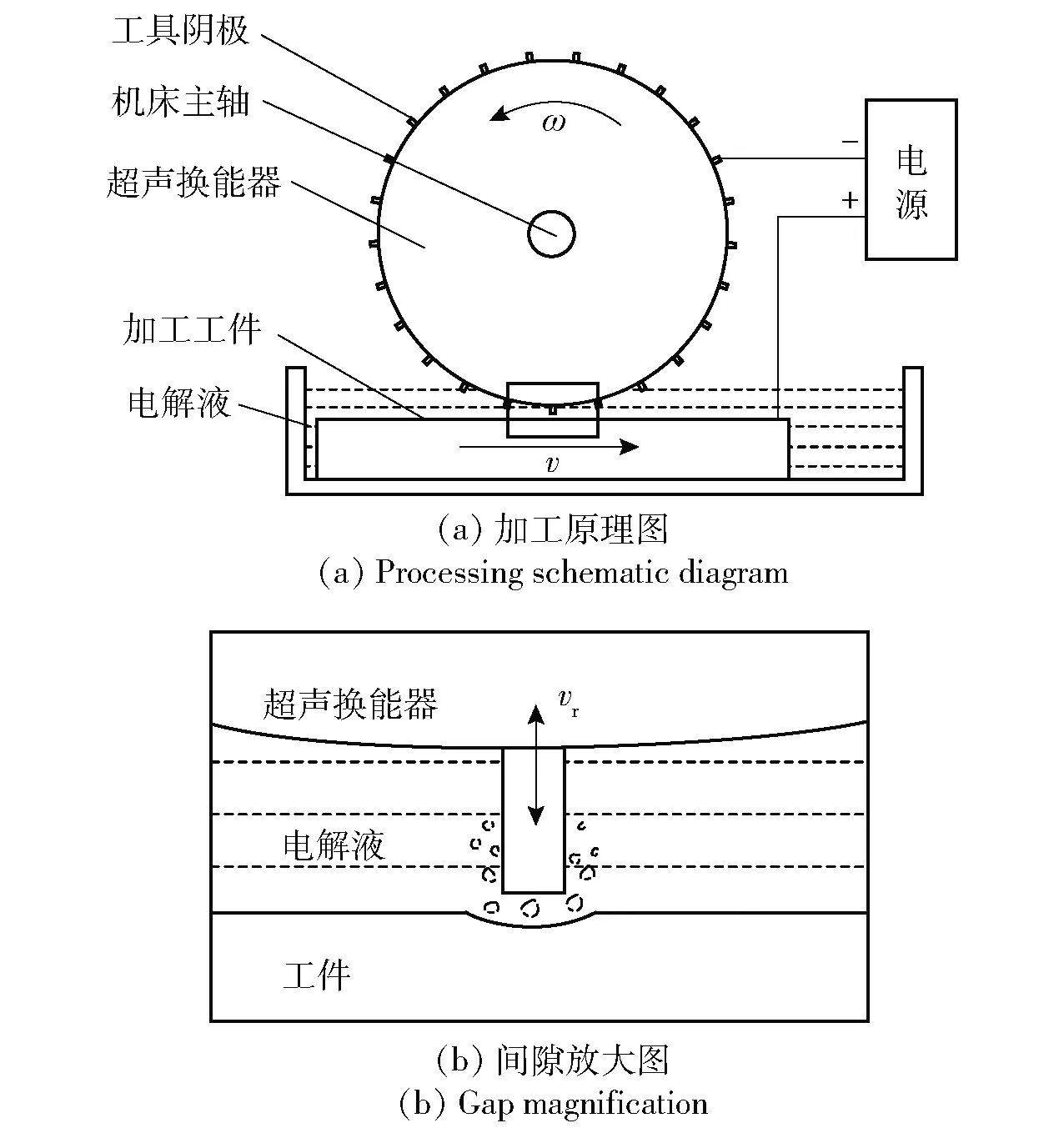
图1 RUR-EMM原理图Fig.1 Schematic diagram of RUR-EMM

2 RUR-EMM理论模型

2.1 气体、液体两相流模型

RUR-EMM间隙内为气体、液体、固体三相流场，其中固体所占比例较小，本文将其忽略。Euler-Euler模型[19]普遍应用于宏观两相流体问题中，该模型将气体、液体两相作为能够互相穿透的介质，并跟踪每一相的平均浓度。相与相之间的速度场互相影响，Euler-Euler模型根据动量平衡方程和连续性方程描述每个相的动力学特性。模型基于以下假设：

1)气泡密度相对于流体密度忽略不计；

2)气泡相对于液体的运动由黏性阻力和压力之间的平衡决定；

3)气体、液体两相处于同一压力场之中。

基于上述假设，建立气体、液体两相流模型的连续性方程：

(3)

式中：ul为液相速度矢量；ug为气相速度矢量；φl为液相体积分数；φg为气相体积分数；ρl为液相密度，ρl=1 221.5 kg/m3；ρg为气相密度,ρg=0.089 9 kg/m3.

间隙中气相迁移方程为

(4)

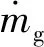
气泡速度方程为

ug=ul+us+ud,

(5)

式中：us为相与相之间的滑移速度；ud为气泡的漂浮速度，

(6)

μ为引起气泡漂移的有效黏度。

将(5)式与(6)式代入(4)式中，得

(7)

2.2 间隙内多物理场耦合模型

RUR-EMM过程中，电化学反应会引起流场与温度场的改变，间隙内存在电场、温度场、两相流场、声场多场耦合情况，各物理场互相促进、抑制，影响材料的成型规律。因此，建立电场- 温度场- 两相流场- 声场理论模型，以研究材料成型规律。

间隙流场可以由运动方程与连续性方程[21]表示为

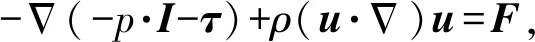
(8)

(9)

式中：p为液体中的压力；I为单位矩阵；τ表示黏度的压力张量；F为单位体积上的力。

体积力为声场产生的声辐射Fa，表示为

(10)

式中：ua为声波在流场传播过程中的振荡速度。

由(8)式、(9)式、(10)式，即可得出间隙流场分布。

在RUR-EMM过程中，温度场变化主要受焦耳热影响，且化学反应热相对于焦耳热可以忽略不计，电场与温度场的关系式为

Q=J·E，

(11)

式中：Q为热源；J为电流密度；E为电场强度。电流密度J可由欧姆定律表示为

J=σE,

(12)

式中：σ为溶液电导率。

在RUR-EMM过程中，间隙内溶液电导率随温度、气体体积分数的变化关系式[22]为

σ=σ0(1+K0(T-T0))(1-φg)A，

(13)

式中：σ0为电解液初始电导率，σ0=7.9 S/m；K0为电导率温度系数；T为电解液温度；T0为电解液初始温度，T0=293 K；A为气体体积分数φg对电导率σ0的影响指数，A=1.5.

其中流体传热规律可由热力学定律[20]表示为

(14)

式中：ρ为流体密度；Cp为固定压力下的流体热通量；u为流体速度场；q为热通量矢量；k为流体导热系数。

热力学公式(14)式可以进一步改写为

(15)

(11)式、(12)式、(13)式代入(15)式，得到流场、电场、温度场、声场耦合方程式为

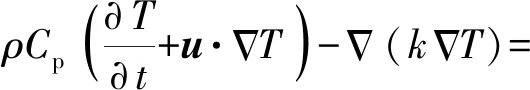
(((1+K0(T-T0))(1-φg)A)J·E)·E.

(16)

根据法拉第第一定律，阳极材料溶解速度与材料表面电流密度和加工时间呈正比，定义材料溶解方程为

(17)

式中：vn为材料溶解速度；η为电流效率；M为阳极材料摩尔质量；ZA为阳极材料化合价；F为法拉第常数；n为法相单元矢量。

3 RUR-EMM间隙多物理场仿真

3.1 模型建立

3.1.1 几何模型

根据RUR-EMM加工原理(见图1)，建立加工间隙区域的几何模型如图2所示：边界1～边界4、边界8为超声换能器表面(已做绝缘)；边界5～边界7为工具阴极表面；边界9、边界11为自由液体流动边界；边界10为阳极工件表面；Ⅰ为加工工具域；Ⅱ为模型计算域。边界条件如表1 所示。

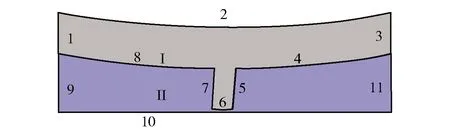
图2 几何模型边界及计算域Fig.2 Boundaries and computational domains of geometric model

3.1.2 网格划分

基于微凹坑成型规律进行网格划分，如图3所示。对工件表面、加工间隙进行网格细化处理，其余部分进行网格粗化处理，以减少计算时间。最终网格总单元数为9 764，平均网格质量为0.854 6，网格质量较好，能够得到较为准确的计算结果。

选择工具阴极中心距工件30 μm处为数据提取点，工件表面为数据提取线(见图3)。

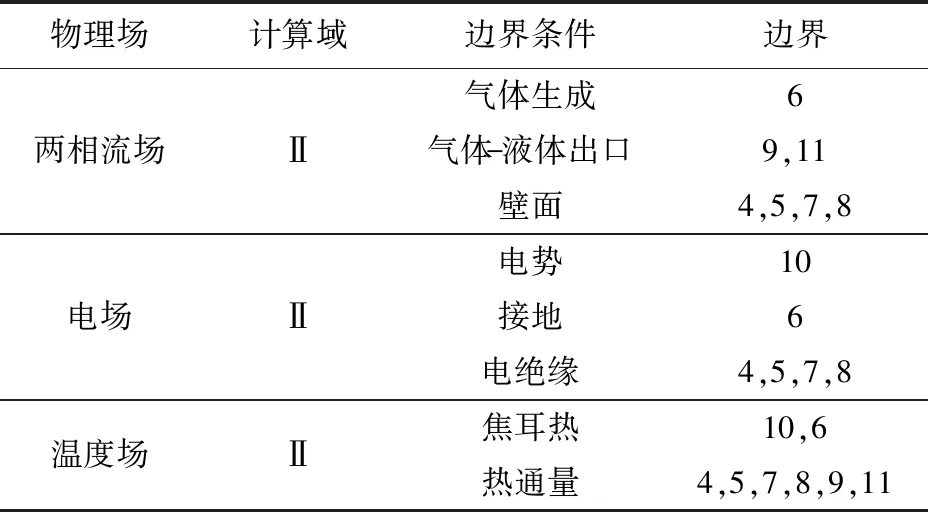
表1 模型边界条件设置Tab.1 Model boundary condition setting

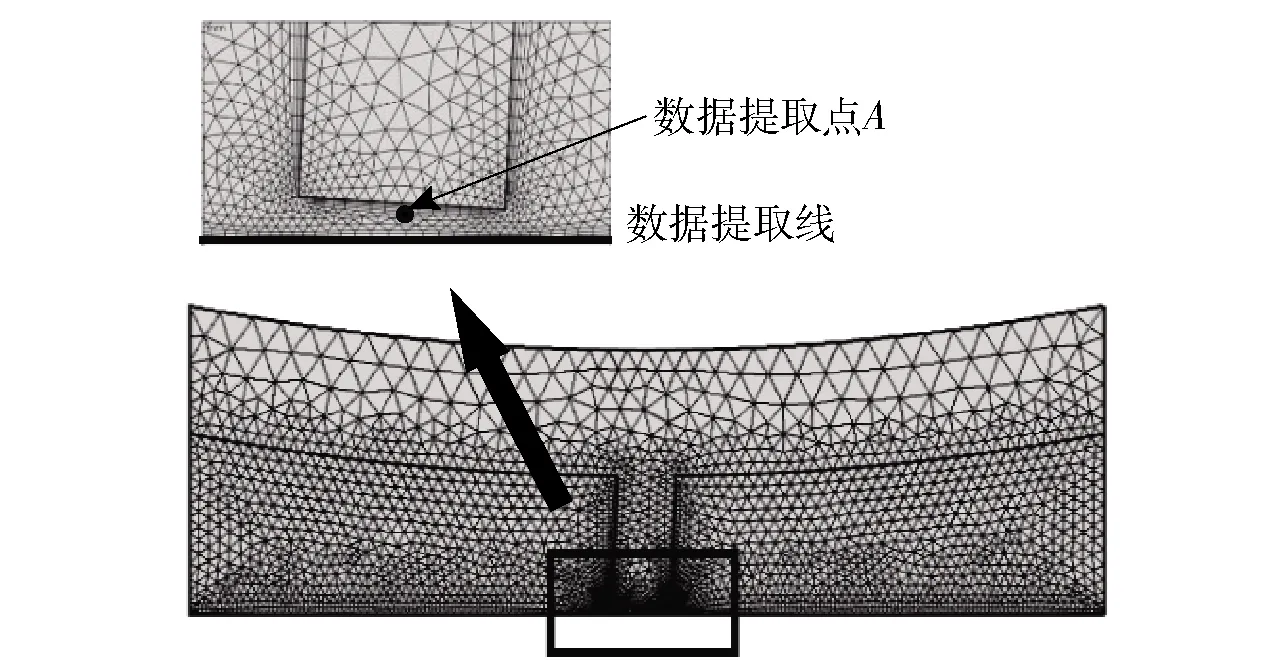
图3 网格划分Fig.3 Mesh generation

3.2 耦合场特性研究

RUR-EMM工况下，间隙内电场、流场、温度场相互影响。电场会引起气泡率与温度的变化，温度与气泡率会导致电导率发生改变，继而影响电场。

在径向超声作用下，工具阴极周期性振动，其振动位移如图4所示。

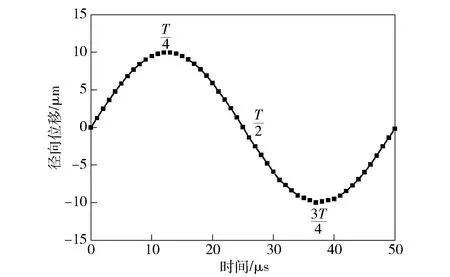
图4 工具阴极振动曲线Fig.4 Vibration curve of tool cathode

3.2.1 间隙流场特性分析

仿真分析结果如图5～图7所示。由图5～图7可知，RUR-EMM工况下，超声激励作用产生间隙脉动流场，促进间隙电解产物排出，使气体体积分数下降。在一个振动周期内，当t=T/2时，电解液受向下冲击的工具阴极影响向外射出，此时流速为最大值0.76 m/s，气体体积分数受间隙流场影响下降至最小值0.23；当t=T时，电解液受向上运动的工具阴极影响流入加工区，流速再次达到峰值0.76 m/s，气体体积分数上升至最大值0.4.

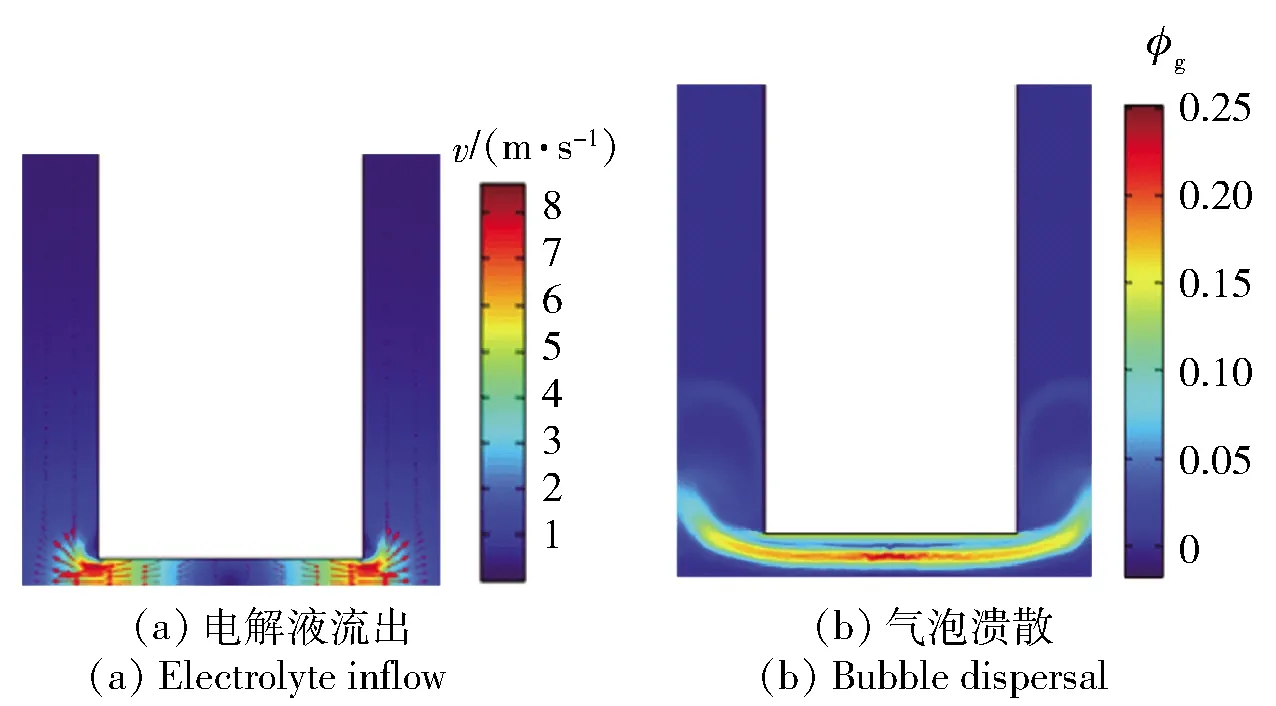
图5 t=T/2时RUR-EMM流场状态Fig.5 RUR-EMM flow field state for t=T/2

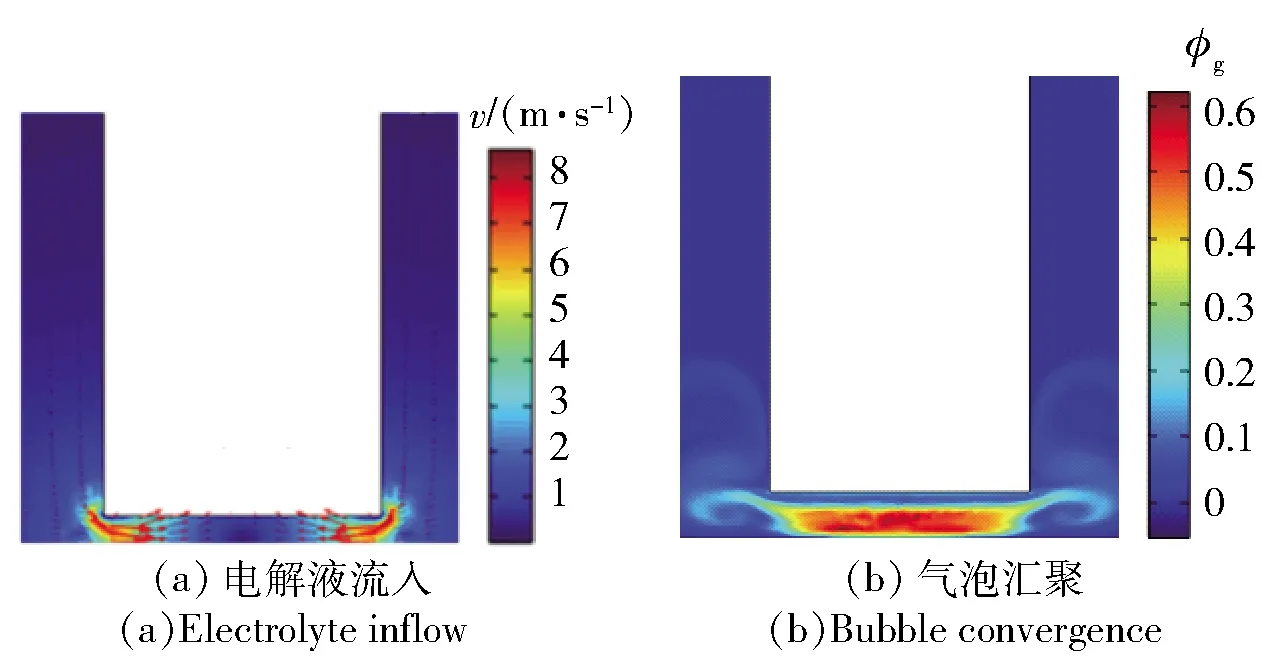
图6 t=T时RUR-EMM流场状态Fig.6 RUR-EMM flow field state for t=T

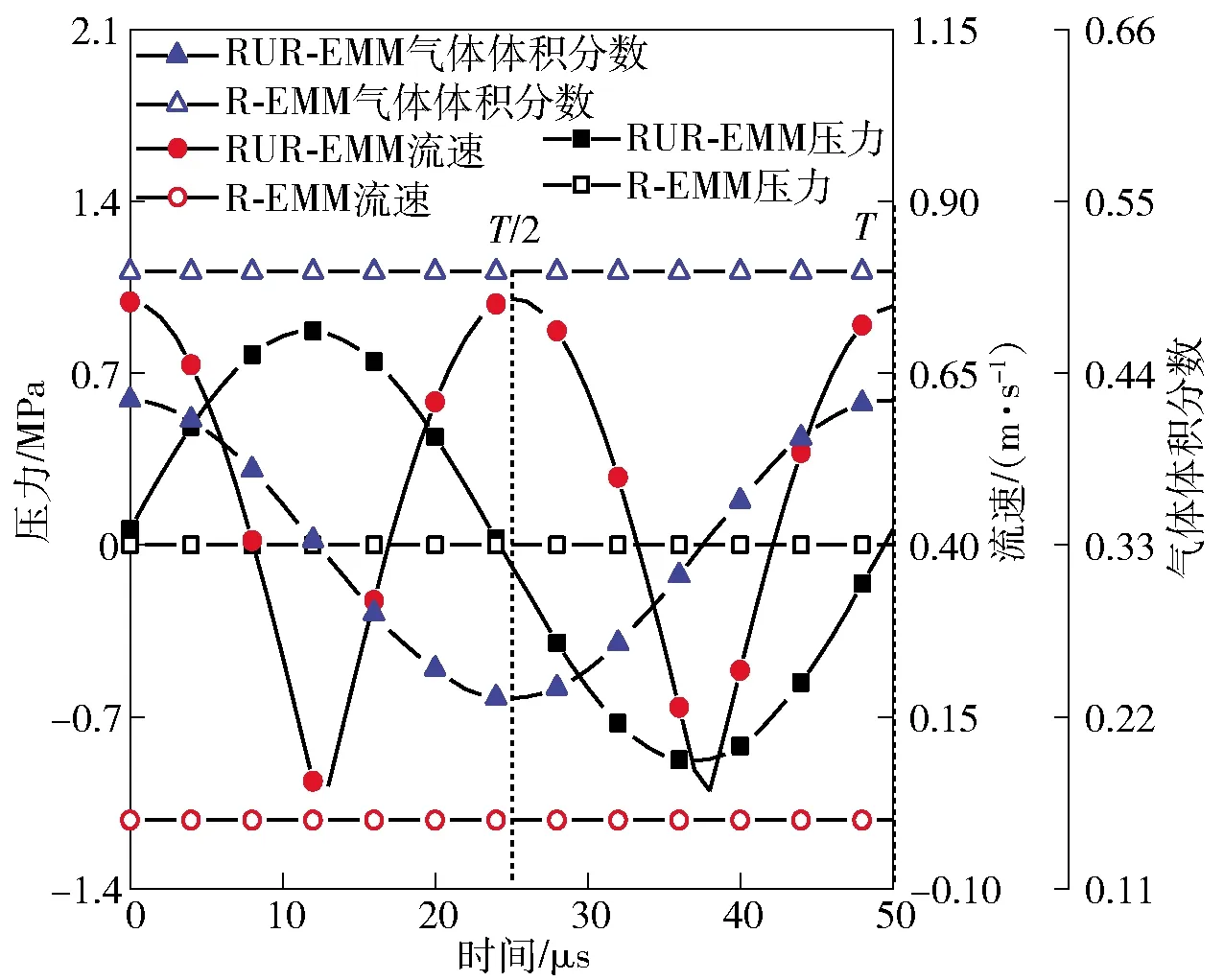
图7 振动周期内流场特性曲线Fig.7 Characteristic curves of flow field during vibration period

R-EMM过程中，间隙流场稳定(见图7和图8)，其间隙流速和压力几乎为0，电解产物排出困难，间隙气体体积分数为0.5，影响材料成形质量。产物气泡混入电解液，在工具阴极边界形成气泡膜，降低间隙内电流密度。在单个周期内，相较于R-EMM，RUR-EMM间隙气体体积分数下降到R-EMM的46%.

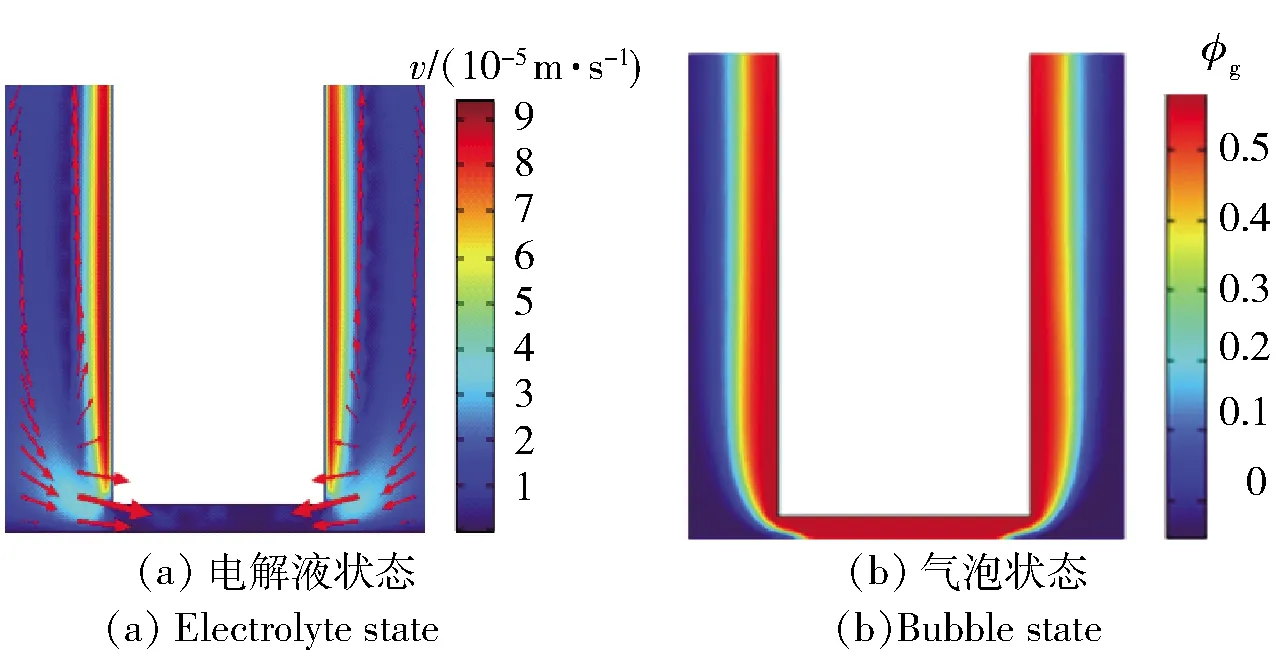
图8 R-EMM流场状态Fig.8 R-EMM flow field state

3.2.2 电场特性分析

提取单个振动周期内的间隙电流密度进行分析，结果如图9所示。

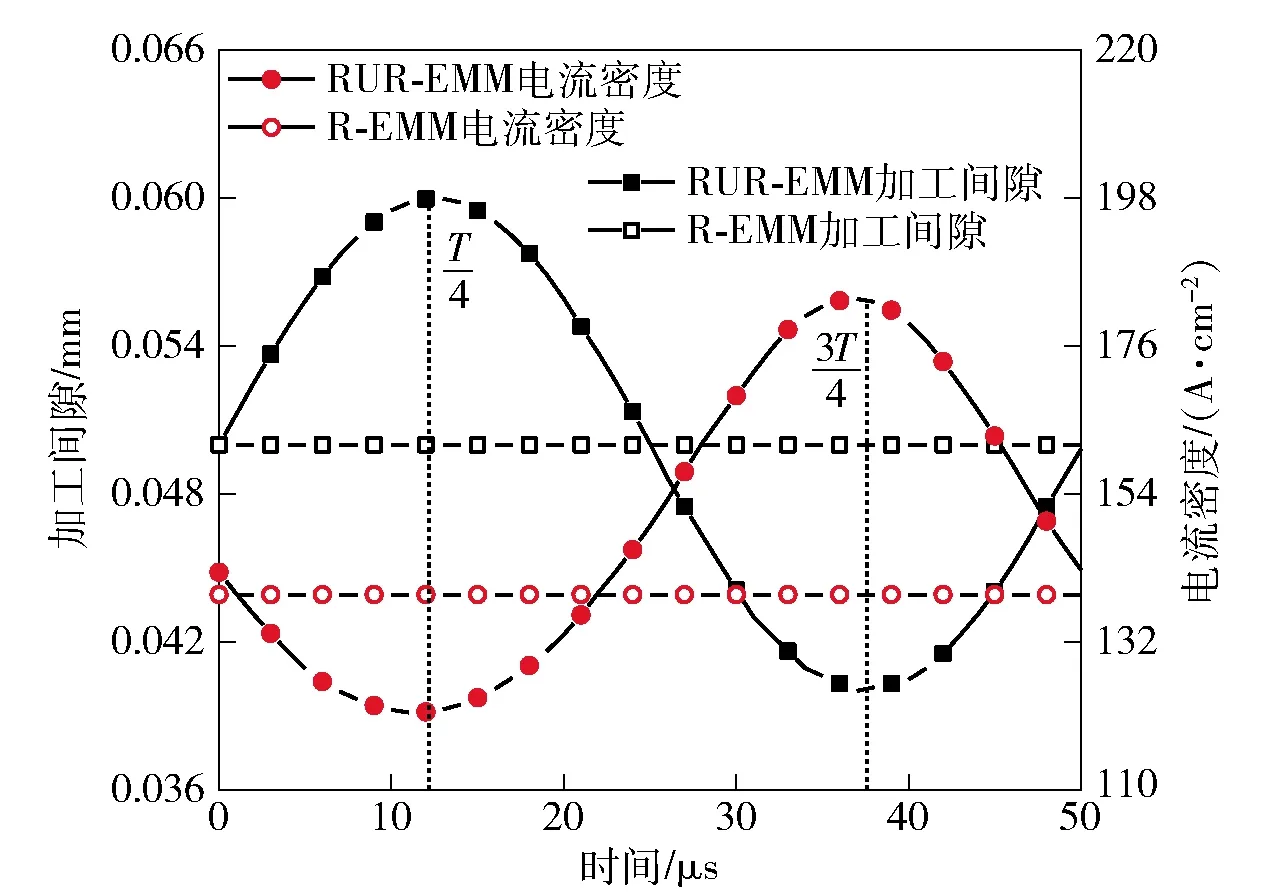
图9 振动周期内电场特性曲线(加工电压10 V) Fig.9 Characteristic curves of electric field during vibration period (applied voltage: 10 V)

在加工电压10 V、R-EMM工况下，间隙电场趋于稳定，间隙电流密度为139.1 A/cm2. RUR-EMM工况下，径向超声使加工间隙产生周期性变化，进而影响间隙电场变化。从图9中可以看出：当t=T/4时，电流密度最小，为121.6 A/cm2；当t=3T/4时，电流密度最大，为183.0 A/cm2. 同时，气体体积分数抑制电流密度大小；气体体积分数比电流密度落后半个周期，使电流密度曲线略微向左偏移。 在单个周期内，相较于R-EMM，RUR-EMM间隙电流密度最大可提高1.36倍。

在滚蚀加工过程中，工具阴极随时间不断运动，使工件表面电流密度分布发生变化，如图10所示，工件表面电流峰值总是处于加工间隙最小处。在10 V加工电压、R-EMM工况下，加工中产生的气泡汇聚于加工间隙内难以排出，导致加工区域中心电导率下降，此处电流密度小于周围区域电流密度，使最终成型凹坑中央存在凸台；RUR-EMM工况下，超声振动促进了间隙产物排出，电解液更新充分，电导率均匀，加工间隙内电流密度变化较为平缓，凹坑底部无凸起。

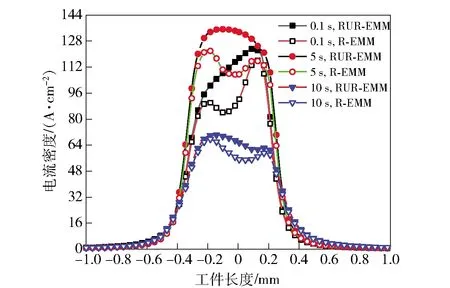
图10 电流密度分布曲线(加工电压10 V)Fig.10 Current density distribution curves (applied voltage: 10 V)

加工过程中，加工间隙与耦合场共同影响间隙电流密度大小，提取R-EMM和RUR-EMM两种工况A点的电流密度，如图11示。由图11可见，两种工况下，电流密度变化趋势基本一致，加工初始阶段，随着工具阴极逐渐靠近工件，加工间隙不断减小，同时在温度场的影响下，电流密度快速上升。之后随着工具阴极逐渐远离加工工件表面，加工间隙逐渐增大，电流密度逐渐下降到最小值。加工过程中，由于不同参数下两种工况的电流密度大小不同，凹坑腐蚀速率不同，导致各自达到电流密度峰值的时间点不同。相同参数下，相较于R-EMM，RUR-EMM间隙电流密度最大可提升1.45倍。

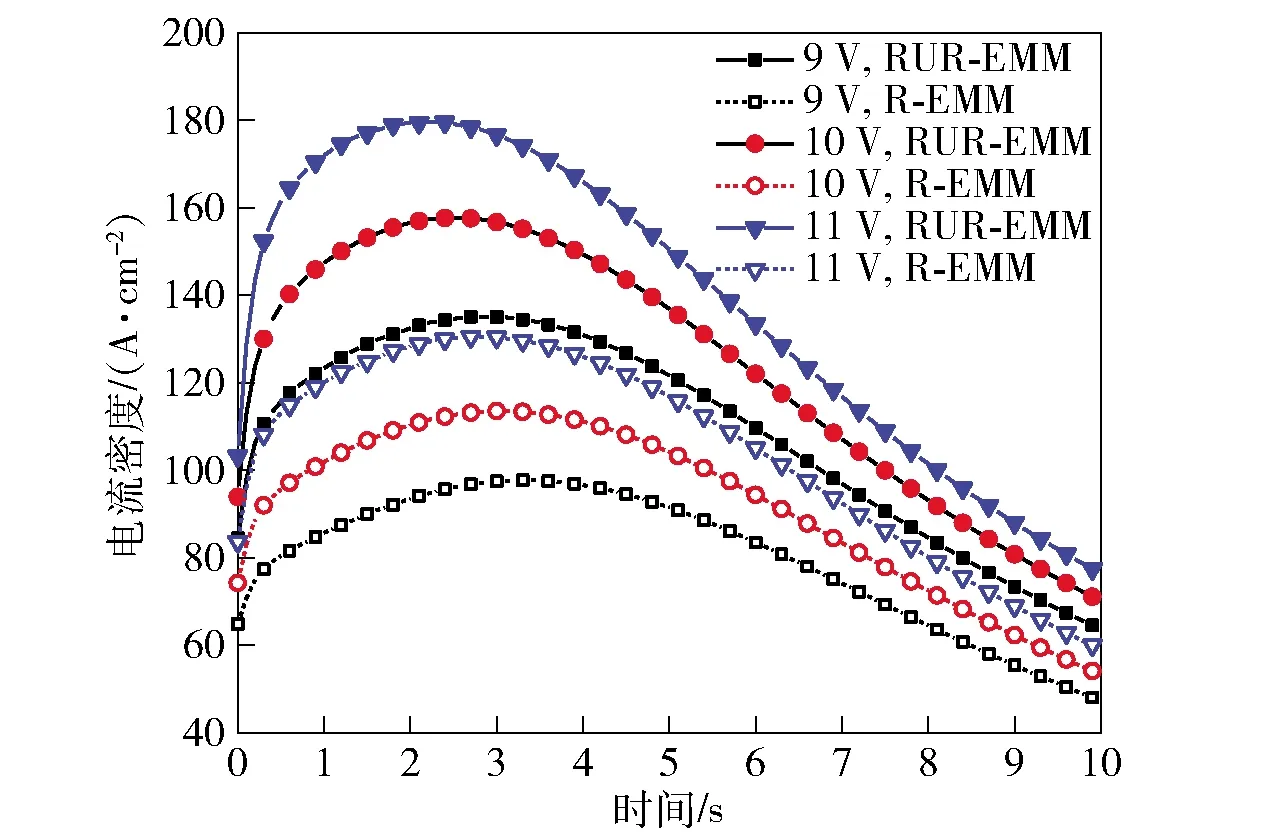
图11 不同加工电压下间隙电流密度曲线Fig.11 Current density curves at different applied voltages

3.2.3 间隙温度场特性分析

间隙内温度场与加工时间、电流密度分布有关，加工过程中电场分布随工具阴极位置而改变，引起温度场分布变化，如图12所示。由图12可见，R-EMM工况下，受电解产物影响，加工区域中心电流密度较小，电化学反应较弱，使加工区域内的温度变化较为平缓；RUR-EMM工况下，径向超声作用间隙流场，促进间隙内产物排出，加工区域中心电流密度受产物影响降低，电化学反应增加，使加工区域内的温度比R-EMM高，变化比R-EMM更为明显。

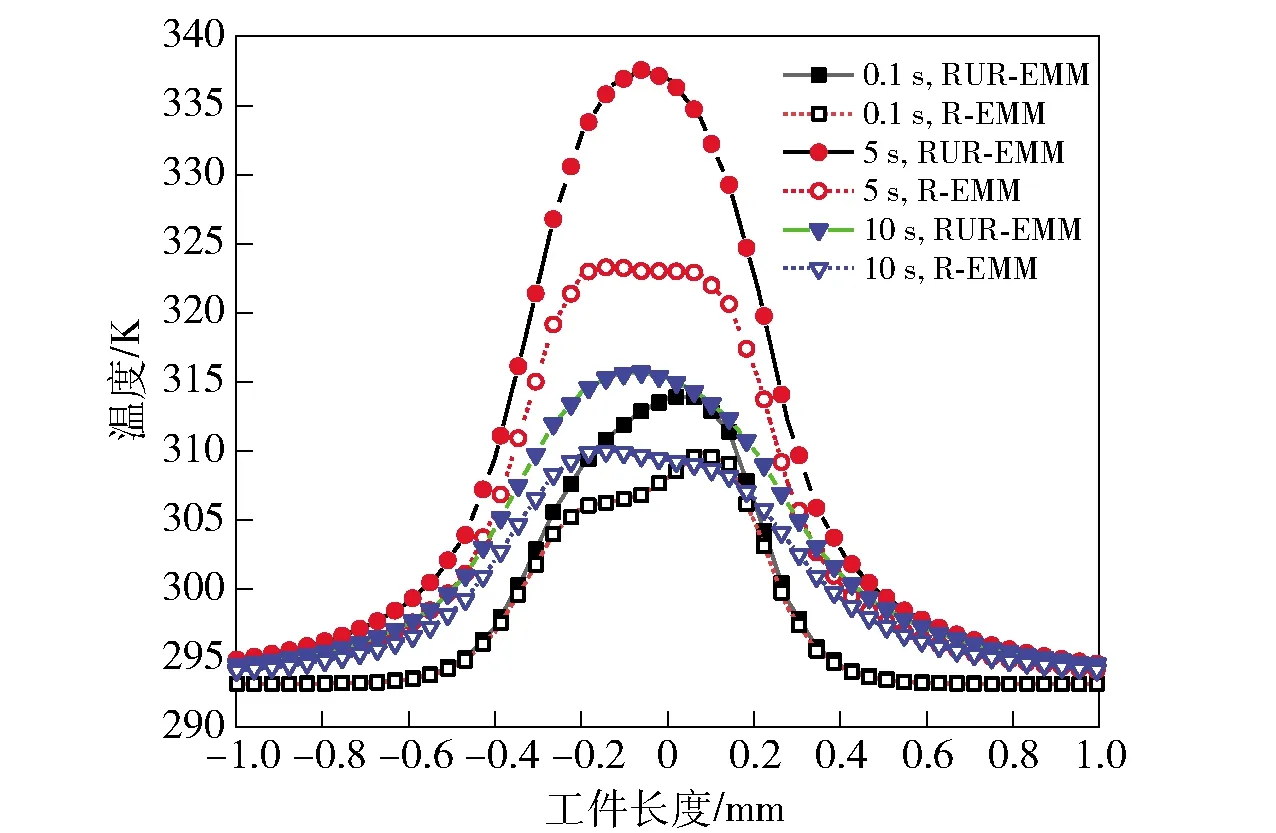
图12 温度分布曲线(加工电压10 V)Fig.12 Distribution curves of temperature in machining gap (applied voltage: 10 V)

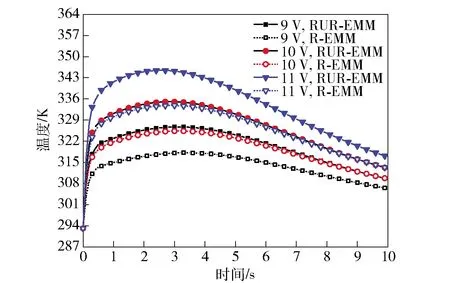
图13 不同加工电压下间隙内温度曲线Fig.13 Gap temperature curves under different parameters

加工过程中参考点A的温度变化如图13所示。由图13可见，加工初试阶段，在温度场与电场的相互促进下，加工间隙内电解液温度迅速上升。随着加工间隙变大，电流密度逐渐下降，电化学反应减弱，间隙电解液温度逐渐降低。RUR-EMM中，在脉动流场作用下，加工间隙内电解液温度下降幅值较为明显。相同参数下，相较于R-EMM，RUR-EMM间隙温度最大提高了3.63%，这是由于RUR-EMM过程中，材料腐蚀反应更为剧烈所致。

4 工艺试验验证

以SS304不锈钢作为工件材料，电解加工前抛光去除表面氧化膜，电极材料选用钨，加工条件如表2所示。

表2 仿真与试验参数Tab.2 Simulation and experimental parameters

4.1 试验平台

基于RUR-EMM原理搭建试验平台，示意图如图14所示。由图14可见，机床控制器连接并控制机床运动，工具阴极固定在机床主轴上进行旋转、平移运动，超声发生器控制工具阴极产生径向超声振动，阳极工件固定在工作平台上，电源正极与阳极工件相连，电源负极与工具阴极相连，通过监测电流示数以确保正常加工。

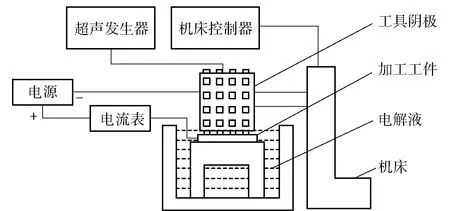
图14 试验平台示意图Fig.14 Schematic diagram of experimental platform

4.2 试验结果对比分析

图15 阵列凹坑织构图(加工电压10 V)Fig.15 Array dimple (applied voltage: 10 V)

图15为10 V电压下两种工况的阵列凹坑织构图。由图15可见，R-EMM阵列凹坑织构中的凹坑中央均有凸台结构，RUR-EMM阵列凹坑织构中，由于径向超声改善了间隙电流密度分布，凹坑中央无凸台结构，凹坑形貌得到改善。利用高速摄影仪测量6个微凹坑的深度与宽度，结果如图16所示。由图16可见，R-EMM工况下，微凹坑宽度波动38.8 μm内，深度波动在2.7 μm以内；RUR-EMM工况下，微凹坑宽度波动29.98 μm内，深度波动在2.9 μm以内。由此可见，两种工况下凹坑具有较好的一致性，试验凹坑形貌与仿真结果基本一致(见图17)。

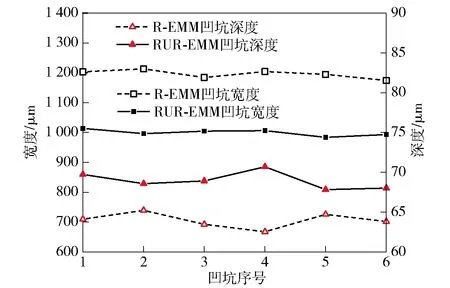
图16 微凹坑宽度与深度(加工电压10 V)Fig.16 Width and depth of dimple(applied voltage: 10 V)

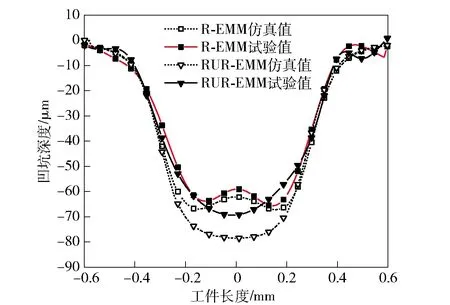
图17 凹坑轮廓对比(加工电压10 V)Fig.17 Comparison of dimple contours (applied voltage: 10 V)

采用日本Olympus公司生产的LEXT4500激光扫描共焦显微镜对10 V电压下成型凹坑截面轮廓进行测量提取，与仿真所得凹坑轮廓曲线进行对比，结果如图17所示。由图17可见， RUR-EMM凹坑轮廓曲线中：试验凹坑最大深度为69.37 μm、截面积为0.041 mm2，仿真凹坑最大深度为78.21 μm、截面积为0.048 mm2，深度误差为12.74%，截面积误差为17.07%；R-EMM凹坑轮廓曲线中：试验凹坑最大深度为63.84 μm、截面积为0.038 mm2，仿真凹坑最大深度为66.91 μm、截面积为0.040 mm2，深度误差为4.81%，截面积误差为5.26%. 由此可见，RUR-EMM凹坑深度较R-EMM提高了8.66%，RUR-EMM材料去除率比R-EMM提高了7.89%.

提取不同加工电压下的凹坑中心截面数据，如图18所示。从图18中可以看出：相同电压下，RUR-EMM的深度与截面积都大于R-EMM，这是因为径向超声作用于间隙流场，使间隙电流密度得到提升； R-EMM与RUR-EMM的深度和截面积都随着加工电压的增加而增大。加工电压从9 V增加到11 V，RUR-EMM工况下，凹坑深度增加28.35%，截面积增加了22.49%，R-EMM工况下，凹坑深度增加28.01%，截面积增加21.90%. 相同参数下，相较于R-EMM，RUR-EMM成型凹坑深度最大提高了14.21%.

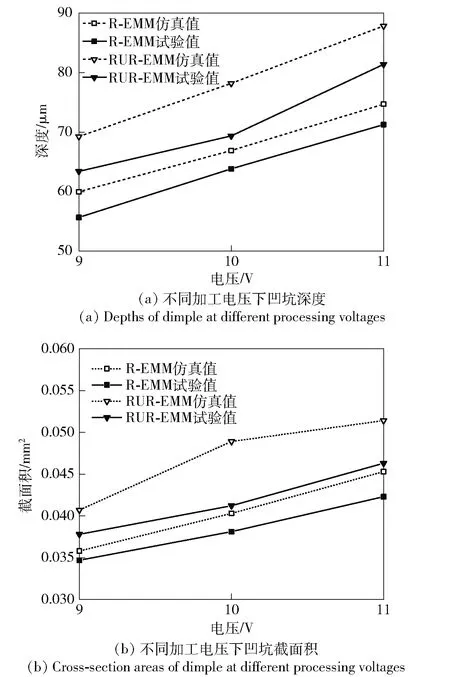
图18 仿真与试验结果对比Fig.18 Comparison between simulated and experimental results

5 结论

本文通过数值仿真建立RUR-EMM多场耦合模型，研究了间隙耦合场变化规律与多场耦合下凹坑成型规律，并通过工艺试验进行了验证。得出主要结论如下：

1)仿真结果证明径向超声能场对流场产生脉动效果，促进了间隙产物排出，改善了间隙电场分布，提升了加工效率。

2)与R-EMM相比，径向超声激励下，RUR-EMM间隙内温度最大提高3.63%，电流密度最大可提高1.45倍，成型凹坑深度最大提升14.21%.

3)通过工艺试验验证，径向超声有效改善了微凹坑的表面形貌并促进了材料的去除，仿真与试验得到的凹坑轮廓曲线基本一致，综合误差控制在17.07%以内。