以毁歼数为判据的高炮毁歼概率试验方法研究
谢杰涛, 吴娟, 王树恩, 范兆军, 韩百刚
(32200部队, 辽宁 锦州 121000)
0 引言
毁歼概率是高炮武器系统关键的综合性指标,对毁歼概率的考核是试验鉴定的重要内容。毁歼概率的试验方法有直接检测和间接检测两类,目前试验鉴定采用的方法是国家军用标准GJBz 20499—98高炮武器系统射击效率评定[1]规定的误差平均法。误差平均法属于以检测脱靶量为依据的间接试验方法,其实质是将通过脱靶量序列得到的随机误差按与时间的相关性分为强相关误差、弱相关误差和不相关误差,并将弱相关误差分解为强相关部分和不相关部分,进而给出毁歼概率的近似积分表达式[2-4]。文献[5]将射击误差序列的共有分量分解为预测值和预测误差,但是其公式推导时只考虑了弱相关误差与初值的相关性,与弱相关误差的状态方差不符。文献[6]以连续脱靶条件下弱相关误差的概率密度函数为基础,给出基于脱靶量序列的毁歼概率精确计算模型,解决了误差分解造成的计算结果近似问题。上述文献中采用的方法均属于以检测脱靶量为依据的间接试验方法,其缺陷在于试验实施复杂,需要立靶密集度、跟踪精度、诸元解算精度和对空射击精度等大量试验数据进行支撑,且计算过程不够直观,试验人员无法在试验现场确定装备性能是否满足指标要求,可能出现试验过程中未毁歼目标但是毁歼概率满足指标的情况。文献[7-14]对毁歼概率的计算进行了研究,但是均不能应用于装备试验鉴定。
对于高炮武器系统毁歼概率指标的回答,必须有试验数据支撑,且具有足够的可信度。为进一步提高试验结果的可信度,本文从毁歼概率的定义出发,探索以毁歼数为判据的直接试验方法,以期为优化试验设计提供理论支撑。
1 判据的选择
高炮武器系统毁歼概率的一种典型表述方式是:在典型航路上,对典型目标、以既定射击方式与弹药消耗实施射击时,目标被毁歼的程度达到既定要求的概率。其中典型航路、典型目标、既定射击方式与弹药消耗在研制总要求中均有规定。
目标被毁歼的程度是毁歼事件最直接的体现,以目标被毁歼的程度作为检验指标,是最直接、可信度最高的检验方法。这类方法可以将武器系统当作一个黑匣子,只需掌握其操作特性,无需分析射击误差、时空分布等特性,更无需了解其内部结构。实战中有关毁歼概率的统计最为可信,就是因为它是最直接而非间接的检验。由于装备试验时无法获得装备实战的数据,需要在试验前对“目标被毁歼的程度达到既定要求”进行可检测且无二义的定义,达到定义的毁歼程度判定目标被毁歼,即“毁歼”事件发生。由于高炮典型目标为敌方装备,试验时难以对真实目标实施射击,通常根据典型目标的战术技术参数,采用高性能靶机进行模拟。这类直接试验方法以实际射击试验中目标(敌方装备或者模拟靶机)被毁歼的数目作为判据,其有效性依赖于“毁歼”事件定义的合理性,同时由于需要对目标产生实际的毁歼,试验成本较高。
另一类试验方法是间接法,包括以检测毁伤元命中数为判据的间接试验方法和以检测脱靶量为依据的间接试验方法。
毁伤元是指着发弹药的弹头、空炸弹药的有效破片、集束弹药的钢柱。命中的毁伤元是导致目标被毁的直接原因,命中是毁伤的前提,没有命中就没有毁伤。当以最小命中数作为毁歼检验指标时,以命中数为判据的间接试验方法即转换为以毁歼数为判据的直接试验方法。
以检测脱靶量为依据的间接试验方法通过测量射击误差的各类分量时空特性,按照基于脱靶量序列的毁歼概率计算模型计算毁歼概率。在试验条件受到以下3种限制时,此类方法可能成为唯一的选择:试验环境不允许射击实弹;靶机性能(如速度、尺寸等)与典型目标的差异较大,无法折算成对典型目标的命中数;所需航次过多,试验成本超出预算。
在靶机性能有效模拟典型目标且试验成本满足要求的情况下,应优先选用以毁歼数为判据的直接试验方法,这也是装备试验鉴定实战化的要求。
2 毁歼事件的定义
毁歼事件的定义应符合作战要求,同时方便试验实施,如目标坠毁、命中目标弹数大于规定值、命中目标导致目标偏航等。由于敌固定翼飞机、巡航导弹、空地制导炸弹等典型目标难以获取,可以采用高性能靶机加挂反射体进行替代。典型目标外形尺寸和结构的详细参数可以通过查阅具体的技术资料获取。
通过实时获取靶机空间位置计算其所代替目标的位置,通过光电测量设备实时测量弹丸空间位置,经解算可以确定弹丸是否命中目标。若测试设备可以捕捉靶机和弹丸姿态信息,则还可以进一步确定弹丸命中目标的位置。
因为靶机的材质与典型目标相差较大,所以靶机的坠毁无法等效为目标的毁歼。但是弹丸对目标的毁伤能力在研制总要求中是明确给出的,因此可以通过检测命中来检测毁歼。进一步地,若可以确定弹丸命中位置,则可以通过命中区域的易损程度直接判断目标是否被毁歼;若只能确定是否命中目标,则可以采用是否达到最少命中数来判定目标是否被毁歼。
本文将毁歼定义为命中目标的弹丸或破片命中数不小于i,即命中数小于i认为目标未被毁歼,命中数大于或者等于i认为目标被毁歼。
3 以毁歼数为判据的试验设计
试验设计的目标为如何利用有限次独立、重复的射击过程,来检验一次射击过程的毁歼概率不小于指标要求P1. 一次射击过程是指武器系统对典型航路上目标以既定的射击方式与弹药消耗实施射击的全过程。单次试验的对象是一次射击过程,虽然点射的射弹之间具有相关性,但是命中毁伤元的弹序并不影响结果的评判。
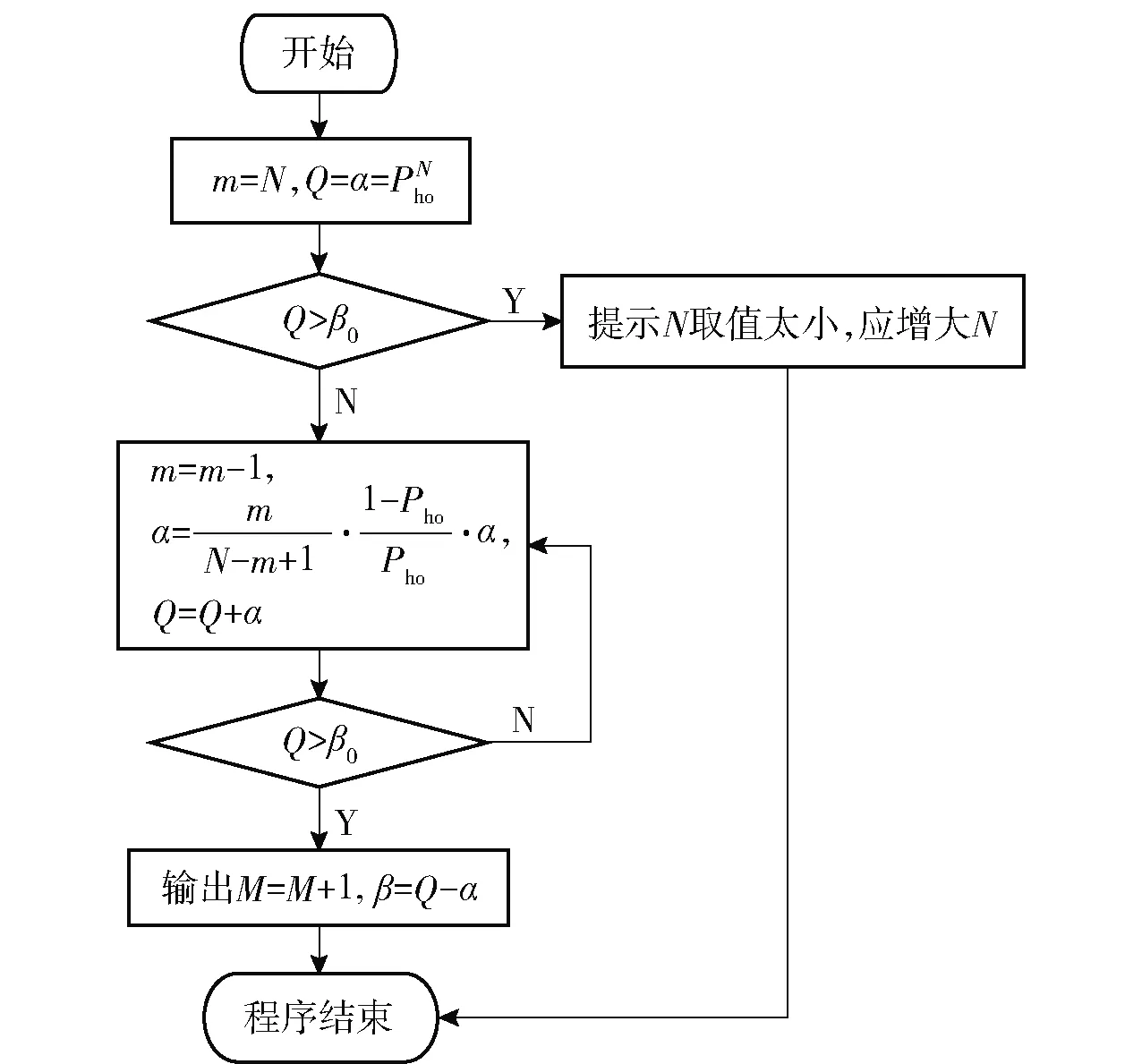
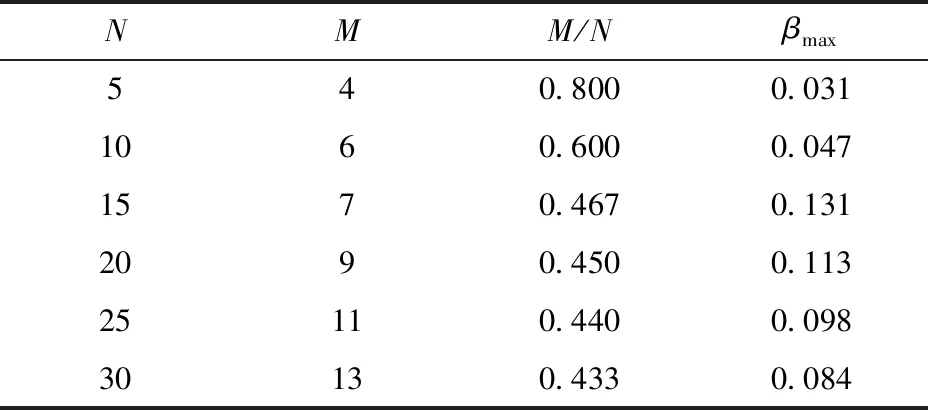
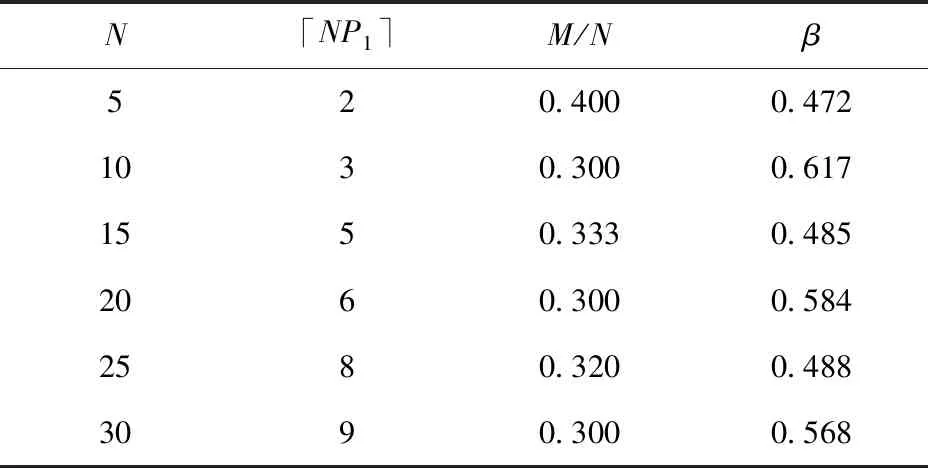
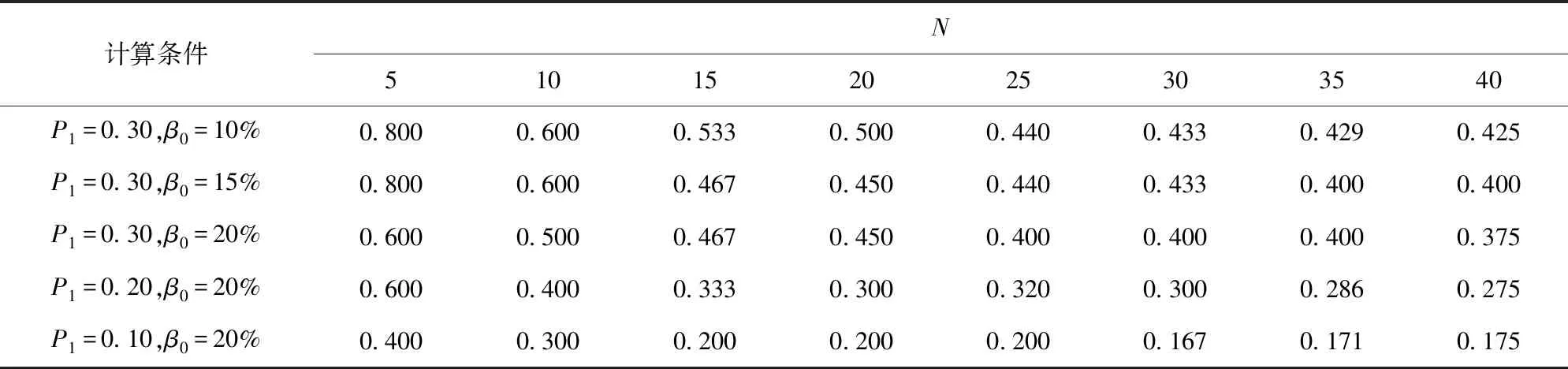
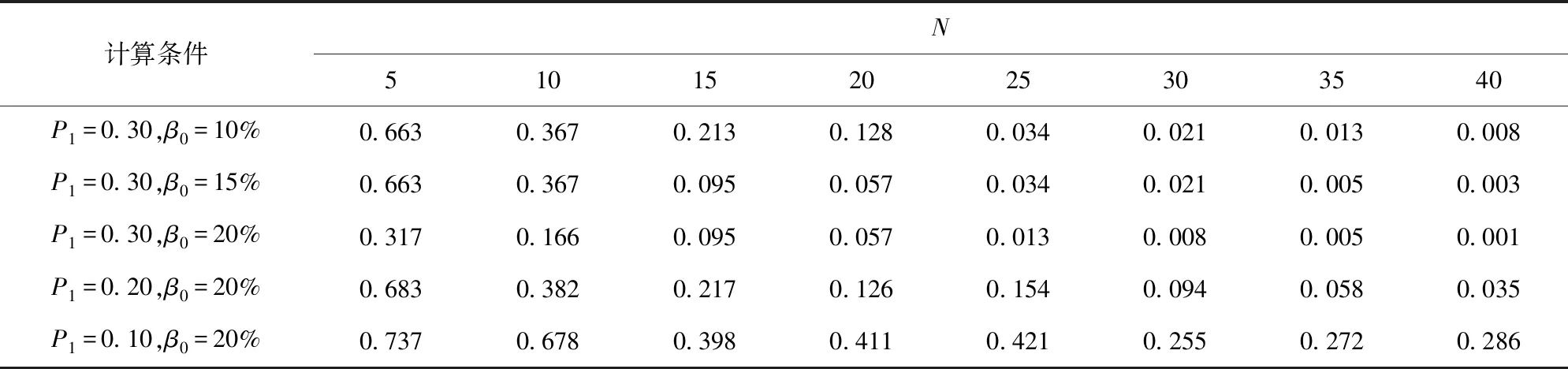
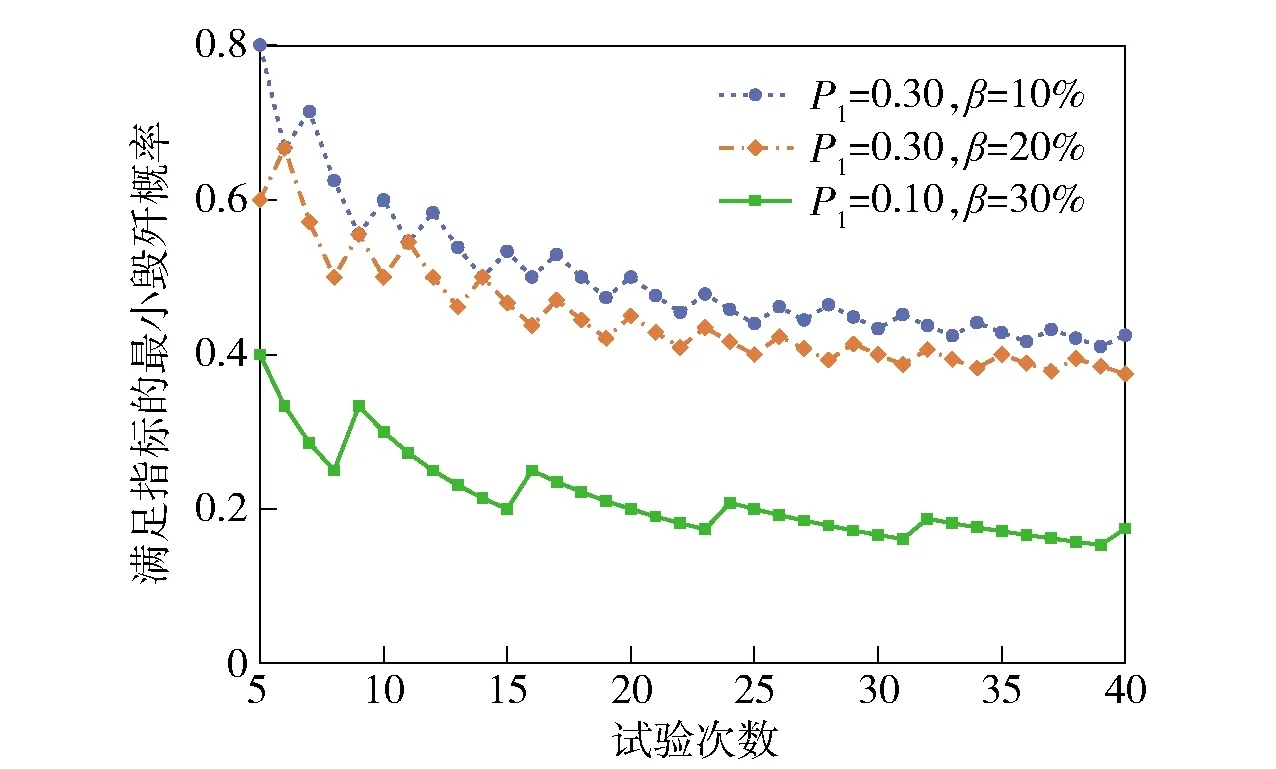
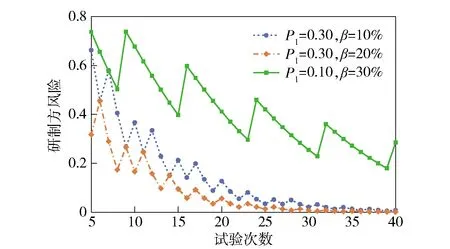
确定好判据和毁歼定义后,试验设计的核心在于确定重复试验的总次数N、预期命中数不少于i的最小试验次数M(即预期最小毁歼数),使得结果的置信度满足要求c. 从军方角度出发,判定武器系统满足指标要求时,武器系统实际的毁歼概率Pho小于P1的概率应小于1-c,即使用方风险β<1-c. 使用方风险β是指在武器系统毁歼概率Pho 由随机理论知,N次独立、重复事件出现k∈[0,N]次的概率服从二项分布,即 (1) 它共有N+1个毁歼频率 (2) 一个待试射击过程毁歼概率的最大似然估计Ph为 (3) 式中:m为毁歼事件发生的次数。 若以Ph作为评判标准,通常认为 (4) 可判定为满足指标,即毁歼数m≥NP1,令 M=「NP1⎤, (5) 此时使用方风险为 (6) 当Pho=P1时,武器系统毁歼概率满足指标,此时β的取值并非使用方风险,但是β(P1)是使用方风险β的一个上界,且是上确界。因此在本文后续的讨论中,用βmax表示N、M给定时使用方风险的最大值,即 (7) 指标P1为已知量,对于确定的N,M可由(5)式给定,此时β和Pho一一对应。Pho对于一个待试射击过程而言是固定不变的,因此当以Ph作为评判标准,β由N唯一确定,即要使β达到要求,只有通过增大试验次数N实现。因此,以最大似然估计Ph作为评判标准,可以得到满足置信度要求的试验次数N,但是N的取值通常较大。在试验实施过程中,可以通过比较预期最小毁歼数M、实际毁歼数m和剩余试验次数来确定试验数据是否能够回答指标,能否提前终止试验。 (6)式对应二项分布的右侧公算,通过查Q(M、N、Pho)表(参见文献[15]),可以由M、N、Pho、β中的任意3个值确定第4个值。设β要求的上限值为β0,为保证β≤β0,则βmax=β(P1)≤β0. 问题转换为如何确定M、N使得Q(M、N、P1)≤β0,该问题可以通过查表解决。 研制方风险α为武器系统毁歼概率Pho≥P1但是被拒收的概率, (8) 从研制方角度出发,武器系统的设计值通常高于其指标值,设武器系统毁歼概率的设计值为Po,有1>Po≥Pho≥P1. 研制方可以采用改进生产工艺等措施,使实际毁歼概率Pho接近甚至达到设计值Po. 对于同样的试验方案,Pho越大,研制方风险α越小。当Pho=Po时,试验后武器系统毁歼概率仍可能被拒收,此时α的取值α(Po)是研制方风险的下界。因此在本文后续的讨论中,用αmin表示N、M给定时研制方风险的最小值,即 (9) 式中:Po对于确定的武器系统是已知量,M、N已经根据使用方风险确定,因此αmin值是可以直接计算得出的。 需要说明的是,当武器系统状态固化后,实际的毁歼概率Pho是未知的固定值,其与指标要求值P1之间大小关系是确定的。因此使用方风险和研制方风险是不能同时存在的,但由于Pho是未知的,其与P1之间的关系也是未知的。当Pho 查表法虽然可以确定M和N,但是受篇幅所限,表格精度不一定能满足要求,主要表现在表格中有效数字的位数是有限的,同时M、N、Pho的选取也是固定的,正好满足精度要求的M和N很可能未在表格中列出。为解决这一问题,本文给出一种Q表的递推计算方法。 (10) 故有 (11) 显然a(m)可以通过递推计算,且无需进行组合运算。 考虑到 (12) 故Q(m)也可以通过递推计算。对于任意N的取值,均可以按照图1计算满足使用方风险要求的预期最小毁歼数M以及使用方风险β. 需要特别说明的是,由于Q(0)=1,图1循环总能退出,不会出现死循环。 图1 依递推计算最小毁歼数流程图Fig.1 Flowchart of recursively calculating the minimum quantity of killed targets 算例1某防空武器系统对一个航次目标射击的毁歼概率战技指标是P1=0.30,要求使用方风险不大于15%. 选择试验总次数N与预期最小毁歼数M,以接受这一指标。 解β0=15%,查Q(M,N,P1)的预期最小毁歼数M和使用方风险上界βmax如表1所示,以毁歼概率的最大似然估计作为评判标准的最小毁歼数「NP1⎤和对应的使用方风险β,如表2所示。 对比分析表1、表2可知,以毁歼概率的最大似然估计作为评判标准得出的M值较小,但是β超过要求的使用方风险,不能采用该方案。综合上述分析可知,应采用使用方风险上界βmax作为标准,来选择试验总次数N与预期的最小毁歼次数M. 表1 由查表法给出的最小毁歼数和使用方 风险上界Tab.1 Minimum quantity of killedl targets and the upper bound of the consumer’s risk given by the look-up table method 算例2当P1=0.30、β0分别为10%、15%、20%时,以及当β0=20%、P1分别为0.20、0.30、 表2 以最大似然估计为评判标准的最小毁歼数 和使用方风险Tab.2 Minimum quantity of killed targets and consumer’s risk based on maximum likelihood estimation 0.40时,使用递推计算满足指标的最小毁歼频率M/N,结果如表3所示。令Po=2P1,计算研制方风险下界αmin的结果如表4所示。 表3 不同条件下满足指标的最小毁歼频率M/N值Tab.3 Minimum kill frequencies to satisfy the indicator under different conditions 表4 不同条件下研制方风险的下界αmin值Tab.4 Lower bounds αmin of producer’s risk under different conditions 将步长设为1,计算表3、表4的数据,结果分别如图2、图3表示,其中图2是抽取表3的第1行、第3行、第5行数据得到的结果,图3是抽取表4的第1行、第3行、第5行数据得到的结果。 图2 满足指标的最小毁歼概率与试验次数关系Fig.2 Relationship between the minimum kill frequency that satisfies the indicator and the total number of tests 图3 研制方风险下界与试验次数关系Fig.3 Relationship between the lower bound of producer’s risk and the total number of tests 分析表3、表4以及图2、图3可知: 1)当毁歼概率的指标要求确定时,使用方风险越高,满足指标的最小毁歼频率越小,对应研制方风险的下界αmin越低。 2)当要求的使用方风险确定时,毁歼概率的指标要求越高,满足指标的最小毁歼频率越大,对应研制方风险的下界αmin越低。 3)虽然在局部略有波动,但是随着N的增大,满足指标的最小毁歼频率和对应研制方风险的下界αmin均大致呈减小趋势。局部波动发生在M增大时刻,当N增大而M不变时,最小毁歼频率和对应的研制方风险的下界αmin均减小。 算例3某型武器系统要求单辆战车的毁歼概率为:对巡航导弹≥50%,对飞机≥30%,对空地制导炸弹≥20%,要求使用方风险不大于20%,选择试验次数N与预期最小毁歼数M,以接受这一指标。 解采用递推计算,毁歼数M对应的满足指标最大试验次数N如表5所示。 假定单辆战车毁歼概率的设计值为:对巡航导弹≥75%,对飞机≥60%,对空地制导炸弹≥40%,则满足指标要求时对应的研制方风险下界αmin如表6所示。 兼顾研制方风险,若要求研制方风险的下界αmin也不大于20%,则对巡航导弹最少试验总数为12次,对应的预期最小毁歼数为8;对飞机最少试验总数为8次,对应的预期最小毁歼数为4;对空地制导炸弹最少试验总数为20,对应的预期最小毁歼数为6. 分析表5和表6可知,对于该型武器系统毁歼概率试验而言,所需的试验总次数和预期最小毁歼数均不大,可以采用以毁歼数为判据的直接试验方法进行试验。 算例4某型武器系统要求对飞机的毁歼概率≥30%,对靶机射击15航次,等效飞机毁歼数8架,按照文献[1]中误差平均法计算的结果为0.547,按照文献[6]中递推计算模型的结果为0.516,要求使用方风险不大于20%,确认能否接受该指标。 表5 毁歼数M对应的满足指标最大试验次数NTab.5 The maximum number of tests that meet the indicator for the quantity of killed targets 表6 最小毁歼数M对应的研制方风险下界αminTab.6 The lower bound of producer’s risk corresponding to the minimum quantity of killed targets 解当N=15、M=17、P1=0.30时,βmax=0.050,即该武器系统实际毁歼概率Pho<30%的概率仅为5.0%,满足使用方风险不大于20%的要求,应该接受该指标。 实际上,当Pho=0.394时,β=0.199;当Pho=0.395时,β=0.201. 在使用方风险不大于20%的前提下,可以认为该武器系统的毁歼概率不低于0.394. 虽然文献[1]的误差平均法、文献[6]的递推计算模型和本文方法都给出了接受该指标的结论,但是对于同样的试验结果,前两种方法均认为实际毁歼概率大于50%,而本文方法认为在要求使用方风险不大于20%的前提下,实际毁歼概率为39.4%. 这是因为本文方法是偏向使用方,充分考虑使用方风险的。需要指出的是,由于缺乏足够数据的支撑,对不同计算方法的比较不具有统计意义,仅能给出直观的结果。 毁歼概率的试验方法包括以毁歼数为判据的直接试验方法,以命中数为判据的间接试验方法和以检测脱靶量为依据的间接试验方法,现行的研究主要集中在最后一种试验方法上。本文从理论上对以毁歼数为判据的直接试验方法进行了梳理,从判据选择、毁歼事件定义、试验设计和递推计算4个方面对以毁歼数为判据的直接试验方法进行了分析,并给出了算例,为直接试验方法的开展提供了理论支撑。以毁歼数为判据的直接试验方法,直观、可信度高、充分考虑使用方风险,在靶机性能能有效模拟典型目标且试验成本满足要求的情况下,应优先选用该方法。需要说明的是,虽然直接试验方法是毁歼概率研究的重要方向,但是综合考虑作战条件、射击精度、目标特性、弹药毁伤效能等诸多因素,以检测脱靶量为依据的间接试验方法,仍将是试验鉴定部门主要的试验方法。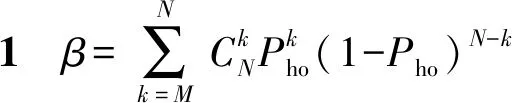
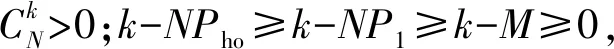
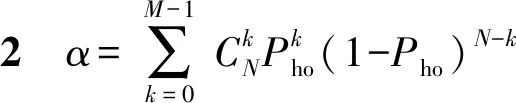
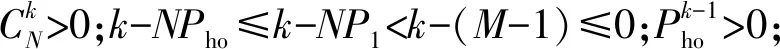
4 Q表的递推计算
5 计算示例


6 结论

