自主水下航行器多终点航路规划的距离正则化混合水平集算法研究
盛亮, 邱志明, 于邵祯, 焦俊杰
(1.海军航空大学 航空基础学院, 山东 烟台 264001;2.海军工程大学 兵器工程学院, 湖北 武汉 430033;3.海军研究院, 北京 102442;4.南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
自主水下航行器(AUV)的多终点航路规划是对AUV单一航路规划的自然延伸,是指在复杂海洋环境下寻求从航行起点到多个终点的最优航路集。适用于AUV单一航路规划的算法,如A*算法、快速搜索随机树(RRT)算法、蚁群优化算法(简称蚁群算法)、粒子群优化算法(简称粒子群算法)、差分进化算法、人工势场法等,理论上也能用于多终点的航路规划,但需要通过多次重复调用算法的整个计算周期来实现,无法一次性规划出所有最优航路。理论上,随着终点数的增多,占用的资源和规划耗时会成倍增加。针对多终点的航路规划问题,探索一次规划出到所有终点的最优航路集的可能性,成为值得关注的研究课题。
Yigit[1]在2011年首次提出利用水平集算法开展考虑海流和固定障碍物影响的AUV航路规划;Lolla等[2]在此基础上验证了水平集算法用于多终点航路规划的可行性和有效性。相比其他算法,水平集算法的优势在于:一是可以通过一次演化计算找到至多终点的所有最优航路;二是能够将海流速度直接纳入演化方程,理论上能够得到考虑海流影响的AUV航路规划最优解析解。文献[3-4]将水平集算法应用于时变的真实海洋环境中并开展了实时海上试验,取得了较好的效果。文献[5]结合随机正交分解方法,提出一种用于在时间最优航路集中寻求最优能耗航路的新的随机正交水平集算法,并基于半实物模型进行了算法验证。在此基础上,基于随机的AUV自身速度大小和方向,文献[6]推导出可用于动态变化海流场中的随机动态正交水平集方程,并给出了数值实现的简化形式,结果表明新的算法是精确和有效的。在国内,刘厂等[7]提出了一种用于AUV航路规划的改进水平集算法。通过采用八邻域方式代替传统四邻域方式来提高计算精度,再采用双快速行进方法改善传统的快速行进法以加快窄带的重构速度,在一定程度上提升了算法执行效率,仿真结果表明改进算法是可靠和有效的。
以上改进算法并没有在效率方面取得明显改善,原因在于这些算法都需要重新初始化窄带,而窄带的频繁初始化是占用计算资源最多、最耗时的部分。针对水平集算法的这一缺点,Li等[8]提出一种无需重新初始化窄带的距离正则化水平集演化(DRLSE)算法。该算法通过引入能量惩罚项即距离正则化项,使得水平集在不断演化过程中,纠正水平集函数与符号距离函数之间的偏差,使之自动约束为符号距离函数而无需再初始化,大大提升了水平集算法的计算效率。
近年来,DRLSE思想在图像分割、拓扑优化得到广泛应用。文献[9-10]为克服DRLSE算法对初始轮廓高度敏感的缺点,提出一种结合C均值聚类方法的混合算法,可用于甲状腺结节图像分割和肝脏肿瘤图像分割。文献[11]采用改进DRLSE模型把图像的局部信息结合到变分能量方程中,用改进的能量方程指导曲线的演化。结果表明,新算法平均消耗时间只需要DRLSE的2.76%,且具有较高的分割准确性。文献[12]基于局部熵提出一种改进的结合边界信息和区域信息的水平集图像分割模型,具备一定的环境自适应能力,增强了抗噪性能和分割不均匀图像的能力。文献[13]结合双向渐进结构优化和DRLSE演化思想,提出一种用于拓扑优化的局部水平集组合算法,且通过实例验证了算法的收敛性和数值稳定性。
本文通过结合局部水平集思想和改进后的距离正则化项,提出一种多项式距离正则化局部水平集(P-DRLLSM)算法,用于AUV的多终点航路规划,避免了窄带的重新初始化,进一步提升了计算效率,并能在一次算法计算周期内规划出到多终点的所有时间最优航路。
1 距离正则化局部水平集算法
1.1 基于传统水平集算法的AUV航路规划模型
1.1.1 水平集算法
水平集算法求解问题的基本思想是:在空间Ω中,构造更高一维的水平集函数φ(x,t),使得在任意时刻t,运动界面Γ(t)就是φ(x,t)的零水平集,即
Γ(t)={x∈Ω:φ(x,t)=0}, ∀t∈R+,
(1)
式中:R+表示正数集合。
为方便表述,水平集函数简写为φ. 从而将不易求解的运动界面Γ上物理量的问题转换为先求解高一维随时间演化的水平集函数,再根据演化时间得出零水平集曲线,即运动界面。以二维空间为例,设l(t)为一条光滑封闭曲线,其随时间而变化,等同于界面Γ. 与之对应的水平集函数为l(t),t时刻l(t)代表的零水平集φ(l,t)=0,对其求导,得
(2)

(3)
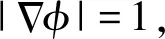
1.1.2 AUV航路规划模型
考虑速度为v(x,t)的海流影响,AUV的运动由零水平集的运动决定,水平集演化方程中的演化速度则由海流速度和AUV自身速度合成,演化方程为
(4)
式中:FAUV(x,t)为AUV自身速度,即AUV相对海流的速度。初始条件为φ(x,0)=|x-ys|,其中ys为AUV航路规划的起点。为保证所求路径为时间最优,要求FAUV(x,t)的方向为水平集函数的梯度方向,则(4)式可进一步化为(5)式的Hamilton-Jacobi方程,即基于水平集算法的AUV航路规划演化方程:
(5)
当AUV到达终点yf即在t=t(yf)时,终点也落在了零水平集内,即φ(yf,t(yf))=0. 此时,t(yf)即为海流影响下的AUV最优航行时间。再通过(6)式进行回溯,即可得到一条时间最优的航行路径:
(6)
1.2 局部水平集算法
为了克服传统水平集算法计算效率低的问题,有学者提出了局部水平集算法[14]。局部水平集的方程可以表示为
(7)
式中:φ′(x,t)为局部水平集函数,简写为φ′;c(φ′)为截断函数,

(8)
γ为局部水平集的半带宽,图1中阴影部分即为局部水平集的窄带,设为D0,γ、β为常量,其值取决于数值计算中模板的宽度,通常设为网格间距Δx的2~6倍,0<β<γ;若采用3阶WENO格式进行偏微分的数值逼近,可取β=2Δx,γ=4Δx;若采用3阶WENO格式,可取β=3Δx,γ=6Δx;F(x,t)为水平集函数的演化速度。设Fk为水平集函数的法向演化速率,则由(1)式可得
(9)

图1 局部水平集模型Fig.1 Model of LLSM

1.3 距离正则化及其改进
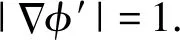

(10)
式中:div(·)表示散度算子;ρ(φ′)=μdp(|φ′|)为扩散速率,μ为扩散系数,dp(φ′)为扩散函数。扩散函数[15]可为
(11)

Wu等[16]对扩散函数进行了如下改进:
(12)
式中:σ为正常数,按照数值经验一般选为4倍网格尺寸。根据逼近理论,任何函数均可由简单多项式最佳逼近,而低阶的简单多项式具有操作方便、运算速度快的特点。本文为进一步提高计算效率,将扩散函数简单多项式化。多项式化后的距离正则化函数为
(13)
与局部水平集函数相结合,多项式距离正则化(P-DRE)扩散函数局部化,则改进后的精简化扩散函数为
(14)
2 改进的距离正则化局部水平集算法用于AUV多终点航路规划
2.1 AUV多终点航路规划模型
不失一般性,考虑单一起始点到多终点的多航路规划。如图2所示,以二维空间为例,在空间Ω中,ys为起始点,yf1、yf2、…、yfq为处于不同位置的q个终点。现需要找到从起点ys到这q个终点的最优航路。当前用于AUV航路规划的寻优算法,如图搜索算法中的A*算法、RRT算法、Voronoi图算法,智能优化算法中的神经网络法、粒子群算法、量子粒子群算法、蚁群算法、遗传算法以及人工势场法等都是在算法的一个计算周期或流程内只能完成起点ys到某一个终点的航路寻优yfg,如需再规划ys到另外终点yfh(其中,1≤g,h≤q,且g≠h)的最优航路,则需要再次开启算法的一个计算周期。

图2 AUV多终点航路规划模型Fig.2 AUV multi-destination route planning model
本文提出利用改进的距离正则化局部水平集算法,在一个计算周期内完成单一起点到多终点的AUV多航路规划,避免了算法计算周期的反复调用,将大大提高计算效率,减少规划用时。
首先,将基于传统水平集算法的AUV航路规划演化方程(4)式局部化,可得
(15)
即有
(16)
进行局部化改进以提高计算效率后,加入改进的简单P-DRE项以避免重新初始化,从而进一步提升计算效率。本文提出的改进后全新的P-DRLLSM方程为
(17)
由(17)式可知,AUV航路规划的P-DRLLSM方程右边由演化项L1(φ′)和正则项L2(φ′)组成,
(18)
(19)
2.2 海流、障碍物及威胁建模
海流会对AUV的水下航行产生不可忽视的影响,轻者使之偏航,重者导致迷航、损毁。本文将可能导致AUV倾覆、迷航乃至损毁的流速较大涡流、内波等区域划定为环境威胁区,类同障碍物,属于禁止航行区域。进行二维航路规划时,将涡流形成的禁航区建模成椭圆,内波区域则建模成不规则的凸多边形。禁止航行区模型如图3所示。

图3 禁止航行区模型示意图Fig.3 Model of forbidden area
使AUV偏航的较小海流大体可分为风海流、梯度流和潮汐流等,在一个较短时间段内,某一片海域的海流通常可以理解为由不同涡流和定常流组成。因此,参考文献[17-18],本文对导致AUV偏航的较小海流采用多个Lamb涡流和定常流的叠加开展建模。海流运动方程可表示为
(20)
式中:vx(r)、vy(r)、vz(r)分别为水平、纵向和垂直方向的涡流速度分量;κ、ξ分别用来描述涡流强度、涡流半径坐标;rie表示第ie个涡流中心的位置,仿真过程中涡流中心位置随机生成;ne为叠加的涡流个数;vCx、vCy、vCz分别为定常流vC在水平、纵向及垂直方向的速度分量。图4为海流运动方程生成的二维海流仿真示意图。由图4可知,该方法能够模拟较为真实的海流运动。

图4 二维海流仿真示意图Fig.4 2D ocean current simulation
除了海流,障碍物和敌对威胁也会对AUV的航行安全产生很大影响,需要在实际航行时避开这些区域。障碍物依照其外形轮廓,按照内波建模方法处理成凸多边形模型(见图5),而AUV航行主要的敌对威胁是水声探测设备。单个水声探测设备的探测区域通常是一种锥型区域,其水平剖面为圆形,因此二维航路规划时,本文将敌对威胁区建模为圆形,三维时以最大探测圆为底、探测距离为高,建模成一个圆柱形区域,如图6所示。多个水声探测设备形成探测阵列时,二维时建模成长方形,三维时处理成长方体。
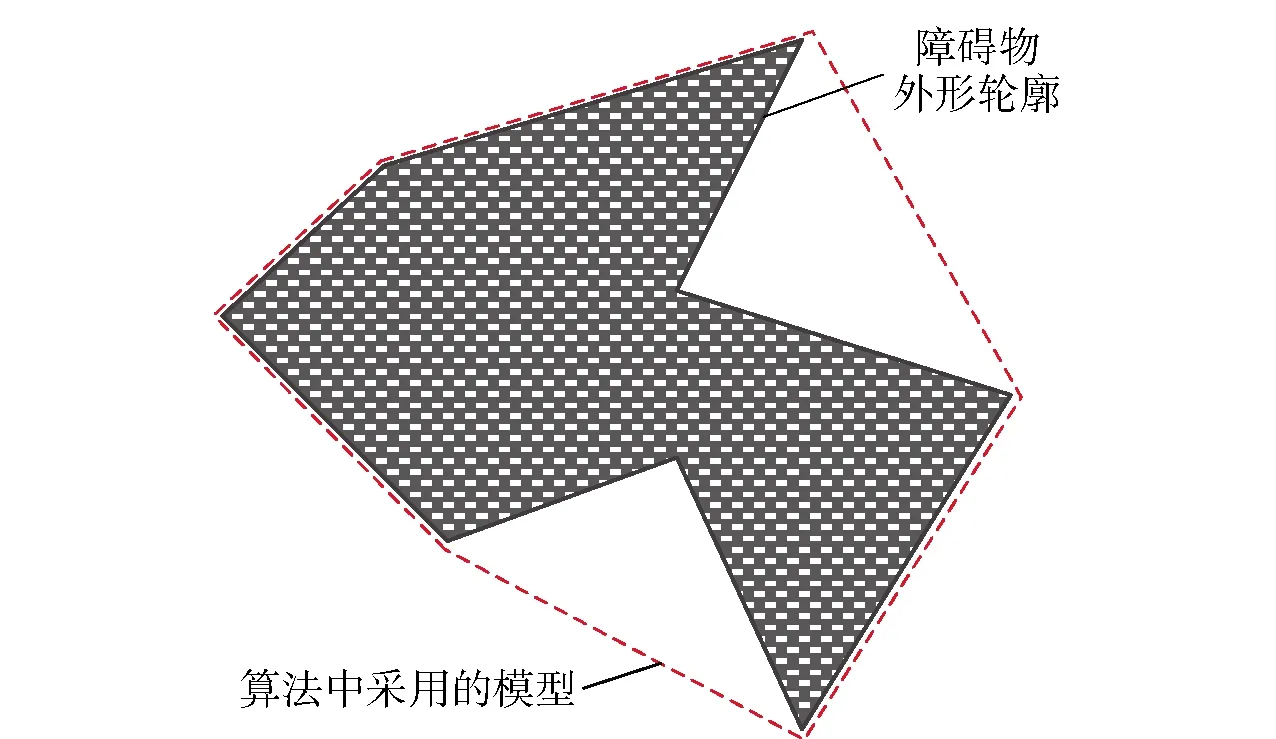
图5 障碍物建模Fig.5 Model of obstacle
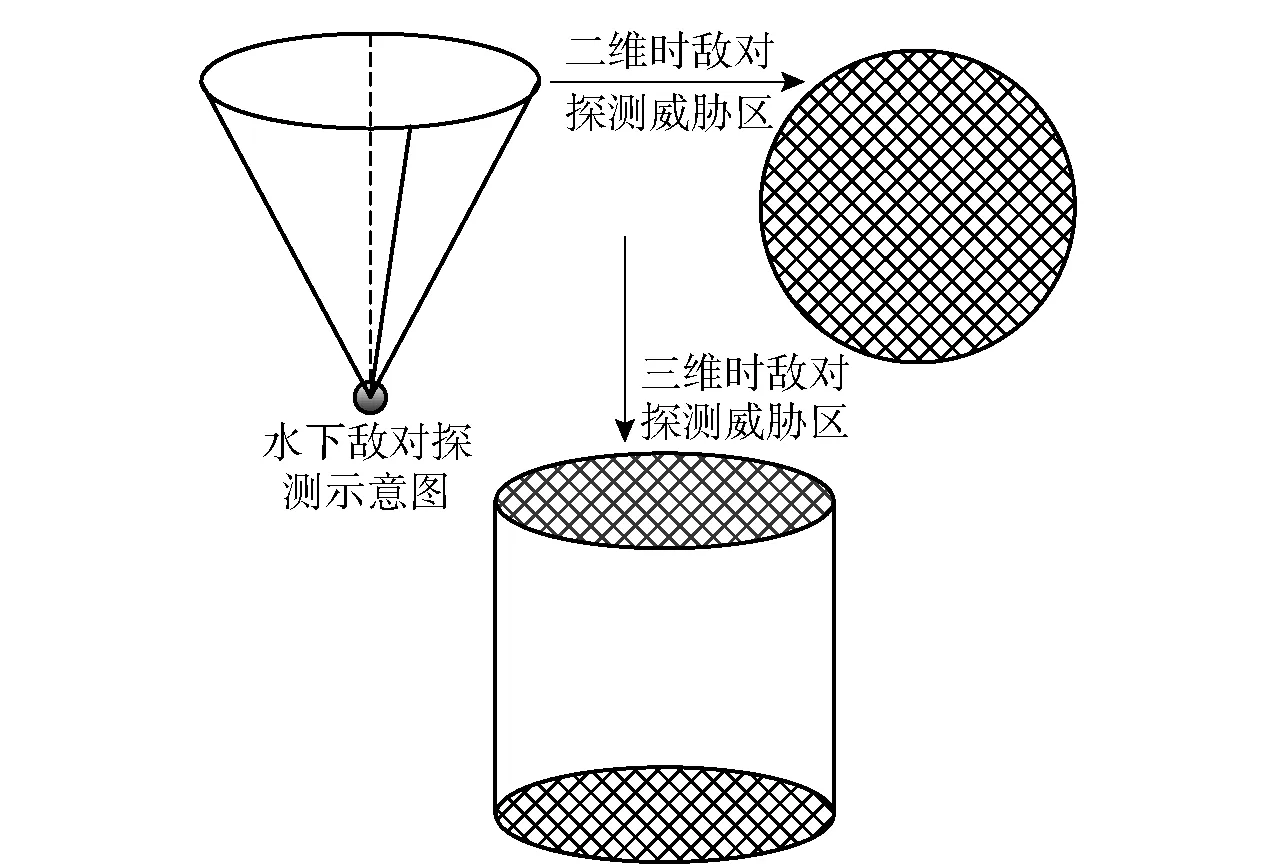
图6 敌对探测威胁区建模Fig.6 Model of hostile detection threat zone
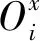
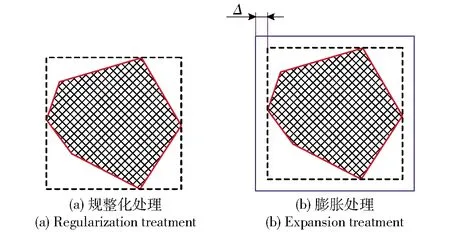
图7 多边形规整化与膨胀处理Fig.7 Regularization and expansion treatments of polygon
2.3 算法数值求解
二维空间中,笛卡尔网格间距设为Δx、Δy,演化时间步长为Δt. 符号φ′i,jn代表φ′(iΔx,jΔy,nΔt),即在nΔt时刻,水平集函数在坐标(iΔx,jΔy)处的值。采用有限差分的迎风格式方法,定义vx、vy为海流速度v(x,t)在笛卡尔坐标系下的分量,则有
(21)
式中:φ′x、φ′y分别为水平集函数在x轴、y轴方向的差分形式。则演化项可离散化为
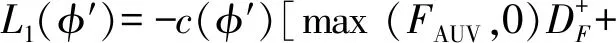
(22)
式中:



(23)
式中:
为保持数值迭代过程中的稳定性,(23)式需满足CFL条件,即
(24)
由(17)式、(22)式及(23)式,可得改进的距离正则化水平集数值迭代方程为
(25)
(25)式中时间步长Δt、网格间距Δx和Δy需满足:
迭代演化从ys开始,初始条件为φ′(ys,0)=0. 经过tg=T(yfg)演化到第1个终点yfg时,φ′(yfg,tg)=φ′(yfg,T(yfg))=0. 以此点为回溯起始点,通过(6)式反向迭代寻找当前点前一时间步长的零水平集中的对应点,直至起始点,从而得到一条从ys到yfg的时间最优路径;然后,从T(yfg)时刻的水平集继续迭代演化,每至一终点yfh(h≠g)就通过回溯找到一条最优路径,直至找到起点到所有终点的最优路径集,算法终止。
2.4 基于P-DRLLSM的AUV多终点航路规划实现
基于P-DRLLSM的AUV多终点航路规划实现步骤如下:
1)初始化水平集函数为符号距离函数,并将AUV航行起点ys置于零水平集上。设置AUV的航行速度FAUV、栅格间距Δx和Δy以及迭代时间步长;设置m个终点yfg,g∈N+且g≤m;设置航路计数器f=0,每找到一条最优航路,则f++.
2)构建考虑海流影响的AUV航路规划局部水平集方程(15)式,海流速度由(20)式给出,其中3个涡流中心位置随机生成。设置障碍物、环境威胁、敌对威胁区域,将其全部设为禁航区,这些区域内海流速度均设为0 m/s,且当水平集方程演化到这些区域时,AUV的速度也设为0 m/s. 从而达到自动避开禁航区的目的。
3)加入P-DRE项,形成P-DRLLSM方程(17)式,依据此方程的离散形式(25)式,在局部区域内沿着零水平集的梯度方向和海流速度的合方向演化水平集函数。每次演化时新加入局部区域外围的点的水平集函数值采用最邻近插值法求得。演化过程中存储每个时间步长的零水平集界面。
4)判断终点集中是否有终点已落入局部水平集的区域内。如果有,则检测新的零水平集界面是否到达终点,如果未到达终点,则返回步骤3,否则转步骤5.
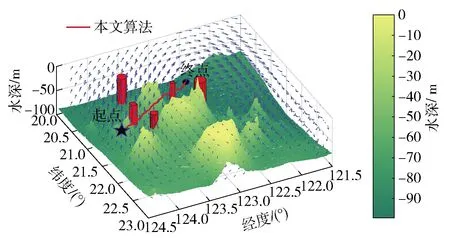
5)后向位置回溯,寻找最优路径。一旦零水平集到达某一终点yfg,则将该终点作为初始点;初始时间t=0 s,通过不断求解方程(6)式,直至在起点ys处收敛,从而获得一条AUV从起点到终点Yfg的时间最优航路。存储该航路,航路计数器f=f+1. 若f 新算法总流程如图8所示。 图8 P-DRLLSM流程图Fig.8 Flow chart of P-DRLLSM 为检验本文所提新算法的性能,分别在模拟海流和真实海流环境下进行仿真实验。实验平台采用数学仿真软件MATLAB R2016a,在Intel Xeon(R)CPU E3-1505M主频3.0 GHz计算机上进行仿真。 3.1.1 二维环境下的仿真实验 仿真环境设定如下:AUV航行空间为二维笛卡尔坐标系下的离散栅格空间,大小为100 m×100 m,栅格间距1 m. 海流由(20)式给出,由3个位置随机生成的涡流和定常流构成,其中每个涡流强度κ和半径ξ的值分别从5~10和3~6中随机选取;定常流速度0.2 m/s,航向60°. AUV速度2.5 m/s. 本文提出的P-DRLLSM算法中,μ为0.5,Δx、Δy均为1 m. 局部化方程(8)式中,γ、β分别设为4和2. 初始化零水平集函数为以起点为圆心、以2 m为半径的圆。量子粒子群算法参照文献[18-19]、蚁群算法参照文献[20-21]开展仿真实验。单终点时,起点坐标为(10 m,15 m),终点坐标为(65 m,75 m)。本文算法规划结果如图9所示。 从图9中可以看出,采用本文所提P-DRLLSM算法进行规划时,AUV尽可能地“骑”着海流航行至终点,且都能避开障碍物和威胁区。规划用时为2.02 s,航行长度为83.55 m,航行时长为29.86 s. 单终点时,3种算法的规划结果对比如图10所示。 图9 二维模拟环境中的单终点航路规划Fig.9 Route planning with single deatination in 2D simulated ocean 图10 二维模拟环境中单终点航路规划对比Fig.10 Comparison of single deatination route plannings in 2D simulated ocean 仿真环境不变对3种算法分别进行100次航路规划,对规划时间、航行时长和航行长度取平均,得到数据如表1所示。 表1 二维模拟环境中单终点时算法性能比较Tab.1 Comparison of the single destination route planning performances of the algorithms in 2D simulated ocean 从表1中可以看出:本文算法规划用时最短,且远低于量子粒子群算法的规划用时,蚁群算法规划速度最慢;航行时长决定算法求得的最优航路质量,航路质量性能基本相当,本文算法规划的航路质量最高,量子粒子群算法次之,蚁群算法最差;在航路长度方面,本文算法规划的最短,量子粒子群算法次之,蚁群算法最长。综上所述可知,本文提出的P-DRLLSM算法在二维模拟环境中,不仅计算效率很高,而且规划的最优航路质量也最高。 单终点航路规划时,3种算法分别规划多次,图11给出了算法的鲁棒性对比情况。 图11 3种算法多次规划所得航路对比Fig.11 Comparison of planned routes of three algorithms 从图11中可以看出,蚁群算法和量子粒子群算法几乎每次规划所得航路都不同,但本文算法每次规划所得最优航路不变,是唯一的,因此本文算法鲁棒性要远好于蚁群算法和量子粒子群算法。 多终点时起点位置不变,终点分别为终点1:(40 m,80 m),终点2(80 m,40 m),终点3(70 m,70 m),终点4(60 m,80 m)。3种算法规划结果对比如图12所示,AUV都能利用海流且避开障碍物顺利抵达终点。 图12 二维模拟环境中多终点航路规划对比Fig.12 Comparison of multi-deatination route plannings in 2D simulated ocean 对3种算法也分别进行100次该条件下的航路规划,对规划时间、航行时长和航行长度取平均,得到数据如表2所示。 从表2中可以看出:与单终点时相比,航路质量和航路长度上变化不大,本文算法性能最好,量子粒子群算法次之,蚁群算法最差;从总规划时间来看,由于本文算法无需重复调用计算周期,随着终点数的增多,规划时间变化不明显,但蚁群算法和量子粒子群算法近乎成倍增加,变化剧烈。由此可见,在4个终点情况下,相比蚁群算法和量子粒子群算法,本文算法计算效率更高,是量子粒子群算法的约14倍、蚁群算法的约34倍。 表2 二维模拟环境中多终点时算法性能比较Tab.2 Comparison of the multi-deatination route planning performances of the algorithms in 2D simulated ocean 3.1.2 三维环境下的仿真实验 三维仿真环境设定如下:以电子海图东经121°30′、北纬20°为坐标原点,以经度增加方向为X轴正方向,维度增加方向为Y轴正方向,水深增加方向为Z轴负方向建立三维规划空间坐标系,范围为0~-100 m. 空间栅格化为100×100×100,X轴、Y轴网格间距为0.03°,Z轴网格间距为1 m. 海底地形建模:取东经121°30′至东经124°30′、北纬20°至北纬23°区域的水深数据,经插值后生成规划空间。 模拟三维海流由(20)式生成,涡流位置随机生成,涡流强度与半径、AUV速度与定常流速度设置与3.1.1节中相同,不同的是涡流有了竖直方向的速度分量。本文算法、蚁群算法、量子粒子群算法的参数设置与3.1.1节中的相同。 单终点时,起点坐标为(122°3′E,21°30′N,-50 m)、终点坐标为(123°39′36″E,22°24′N,-40 m)下3种算法规划结果对比如图13所示。图13中,红色圆柱为经过规整、膨胀处理后的敌方探测威胁区,红色长方体为处理后的障碍物或环境威胁区。 图13 三维模拟环境中单终点航路规划对比Fig.13 Comparison of single destination route plannings in 3D simulated ocean 从图13可以看出,在模拟环境下的单终点航路规划时,3种算法都能在避开障碍物和威胁区的情况下找到时间最优的安全航路。对3种算法分别进行100次航路规划,对规划时间、航行时长和航行长度取平均,得到如表3所示的数据。 表3 三维模拟环境中单终点航路规划时算法 性能比较Tab.3 Comparison of the single destination route planning performances of the algorithms in 3D simulated ocean 从表3中可知,与二维模拟环境中所得结论相同,本文算法在规划时间和所求航路质量上最佳,量子粒子群算法次之,蚁群算法最差。 多终点时,起点坐标不变,起点坐标为(122°3′E,21°30′N,-40 m),共设4个终点,各终点坐标分别为终点1(123°39′36″E,22°24′36″N,-45 m)、终点2(123°54′E,22°12′30″N,-30 m)、终点3(122°24′E,22°24′N,-40 m)、终点4(123°54′E,21°54′30″N,-25 m)。规划结果对比如图14所示。 从图14中可以看出,模拟环境下的多终点航路规划时,3种算法都能在避开障碍物和威胁区情况下找到至各个终点时间最优的安全航路集。对3种算法分别进行100次航路规划,对规划时间、航行时长和航行长度取平均,得到数据如表4所示。 图14 三维模拟环境中多终点航路规划对比Fig.14 Comparison of multi-destination route plannings in 3D simulated ocean 表4 三维模拟环境中多终点航路规划时算法性能比较Tab.4 Comparison of the multi-destination route planning performances of the algorithms in 3D simulated ocean 从表4中可知:在三维模拟环境中进行多终点的航路规划时,本文算法的规划时间和所求航路质量仍然最佳;蚁群算法所求最优航路质量性能要稍优于量子粒子群算法;计算效率方面,量子粒子群算法要优于蚁群算法。 为了验证本文算法在真实环境下的性能,在3.1.2节三维规划空间建模基础上,将模拟海流替换成真实三维海流,从某海流分析系统中提取出东经121°30′至东经124°30′、北纬20°至北纬23°范围某一时间区间的真实海流数据文件,此范围的海流速度范围为0~0.7 m/s,平均海流速率为0.5 m/s. 单一终点的航路规划实验中,AUV速度为1.5 m/s,起点设为:123°39′36″E,21°48′N,-40 m;终点为:122°15′E,20°15′N,-50 m. 本文算法的规划结果如图15所示。 图15 真实海流中单终点三维航路规划Fig.15 3D single deatination route planning in real ocean current 图15中红色长方体为经过规整、膨胀处理后的障碍物区,红色圆柱体为经过处理后的敌对探测威胁区。从图15中可以看出:AUV能够顺流航行且能够很好地避开障碍物和威胁区,以最优时间到达终点;算法规划用时18.89 s,航行长度为165 km,航行时长33.34 h. 真实海流环境下单一终点航路规划时,本文算法与量子粒子群算法及蚁群算法规划结果对比如图16所示。 图16 实际环境中单终点航路规划对比Fig.16 Comparison of single destination route plannings in real ocean 对3种算法分别进行100次航路规划,对规划时间、航行时长和航行长度取平均,得到数据如表5所示。 表5 真实海流中单终点航路规划时算法 性能比较Tab.5 Comparison of the single destination route planning performances of the algorithms in real ocean current 从表5中可以看出,在单终点航路规划时,本文算法与蚁群算法和粒子群算法的规划时间、航行时间和航行长度虽然都在一个数量级上,但是本文算法规划时间和航行时间均最短,说明本文算法单终点航路规划时的计算效率与所求最优航路质量均优于蚁群算法和粒子群算法。 单终点航路规划时,对3种算法分别规划3次,各得到真实海流环境下的3条航路,航路性能数据对比如表6所示。 从表6中可以看出,蚁群算法和量子粒子群算法几乎每次规划所得航路都不同,但本文算法每次规划所得最优航路不变,是唯一的,因此在真实海流环境下,本文算法鲁棒性也远好于蚁群算法和量子粒子群算法。 表6 3种算法多次规划所得航路对比Tab.6 Comparison of routes in multi-planning by three algorithms 多终点航路规划时,起点坐标为(124°12′E,21°39′N,-40 m),共设4个终点,各终点坐标分别为终点1(123°54′E,20°18′N,-50 m)、终点2(123°27′E,20°27′N,-30 m)、终点3(122°51′E,20°54′N,-30 m)、终点4(123°36′E,21°42′36″N,-50 m)。3种算法的航路规划结果如图17所示。 图17 实际环境中多终点航路规划对比Fig.17 Comparison of multi-destination route planning in real ocean 多终点航路规划时,对各个算法分别进行100次航路规划,对规划时间、航行时长和航行长度取平均,得到如表7中所示数据。 表7 真实海流中多终点航路规划时算法性能比较Tab.7 Comparison of the multi-destination route planning performances of the algorithms in real current 从表7中可看出:真实海流环境下的多终点航路规划时,蚁群算法规划的航行长度最长,量子粒子群算法和本文算法规划航行长度基本相当;本文算法航行时间最短,量子粒子群算法次之,蚁群算法最长;蚁群算法规划时长是量子粒子群算法的约1.6倍,是本文算法的约6.4倍。这也进一步验证了前文中的理论分析,本文算法不仅所求航路质量更优,更为重要的是,随着终点数增多,蚁群算法和量子粒子群算法总的规划时间近乎成倍增长,而本文算法总的规划时间增加很慢,从单终点的18.89 s增加到4个终点的21.8 s. 由此可见,不论模拟海流环境下还是真实海流环境下,在多终点航路规划中,终点数越多,相较于蚁群算法和量子粒子群算法,本文算法的计算效率越高,算法性能得到了进一步验证。三维环境中的多次航路规划也表明,本文算法鲁棒性好于蚁群算法和量子粒子群算法。 传统的水平集算法用于航路规划时需要周期性地重新初始化窄带,导致规划效率不高;典型的智能算法,如蚁群算法和量子粒子群算法进行多终点的航路规划时,只能通过反复调用算法的整个计算周期来实现,占用资源多、规划时间长。本文将传统水平集函数局部化,引入P-DRE项,推导了新的离散迭代方程,省去了重新初始化过程,提高了水平集算法的计算效率;此外,多终点的多条最优航路获得是通过水平集函数的不断演化、在一个计算周期中实现的,进一步提高了多终点航路规划的计算效率,且都能找到避开障碍物和威胁区的最优安全航路。仿真结果表明,同等条件下,相比于蚁群和量子粒子群算法,本文提出的新航路规划算法寻优质量更高、规划时间更少、鲁棒性更好,尤其适用于多终点的多航路规划场景。
3 实验结果与分析
3.1 模拟海流下的仿真实验

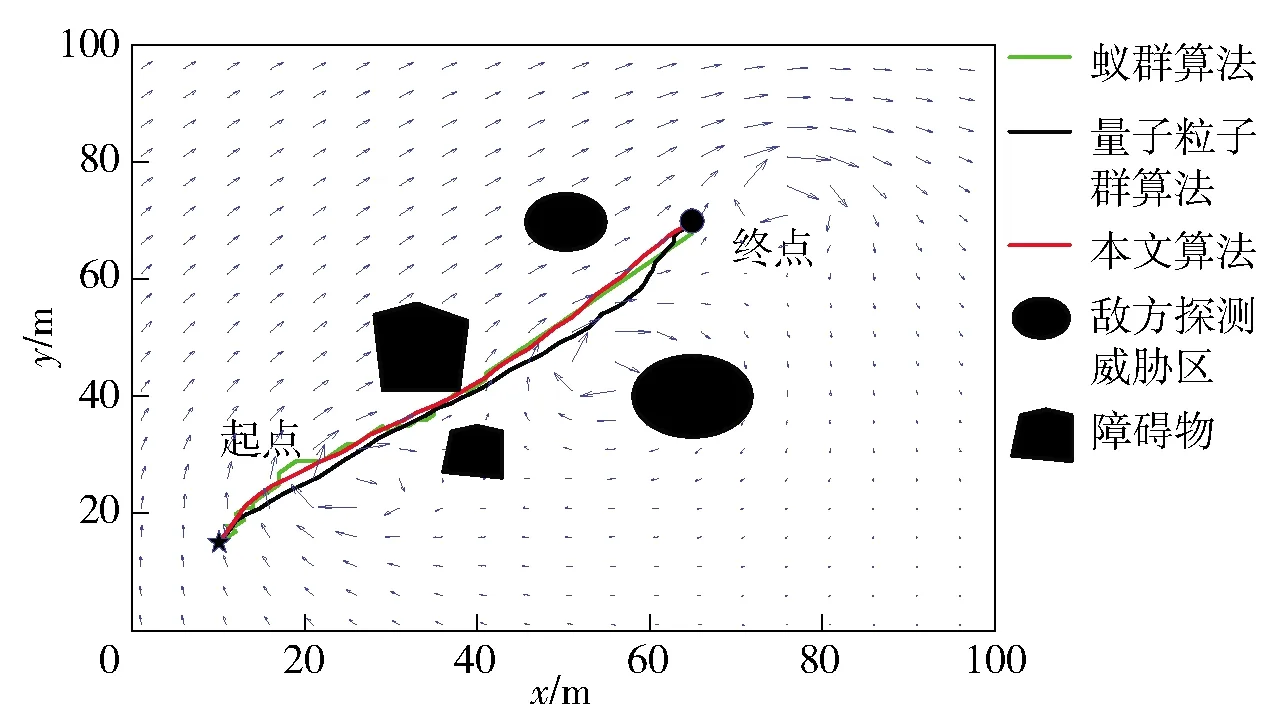

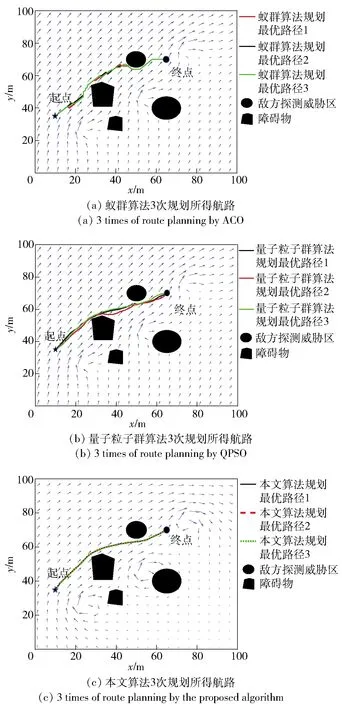


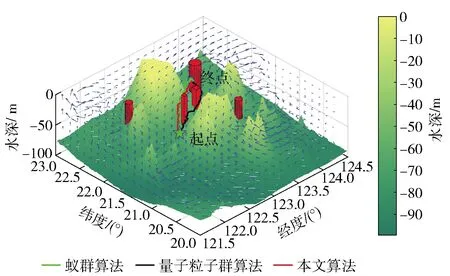
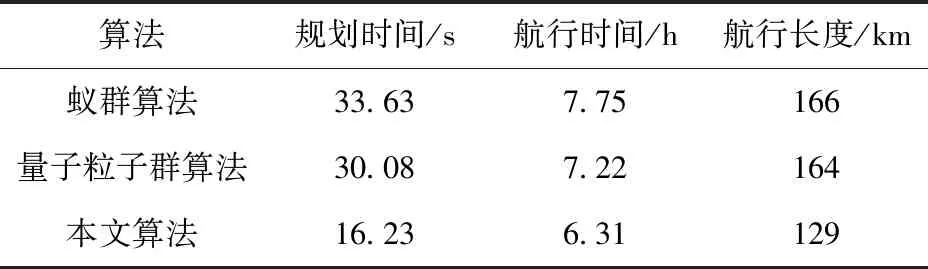
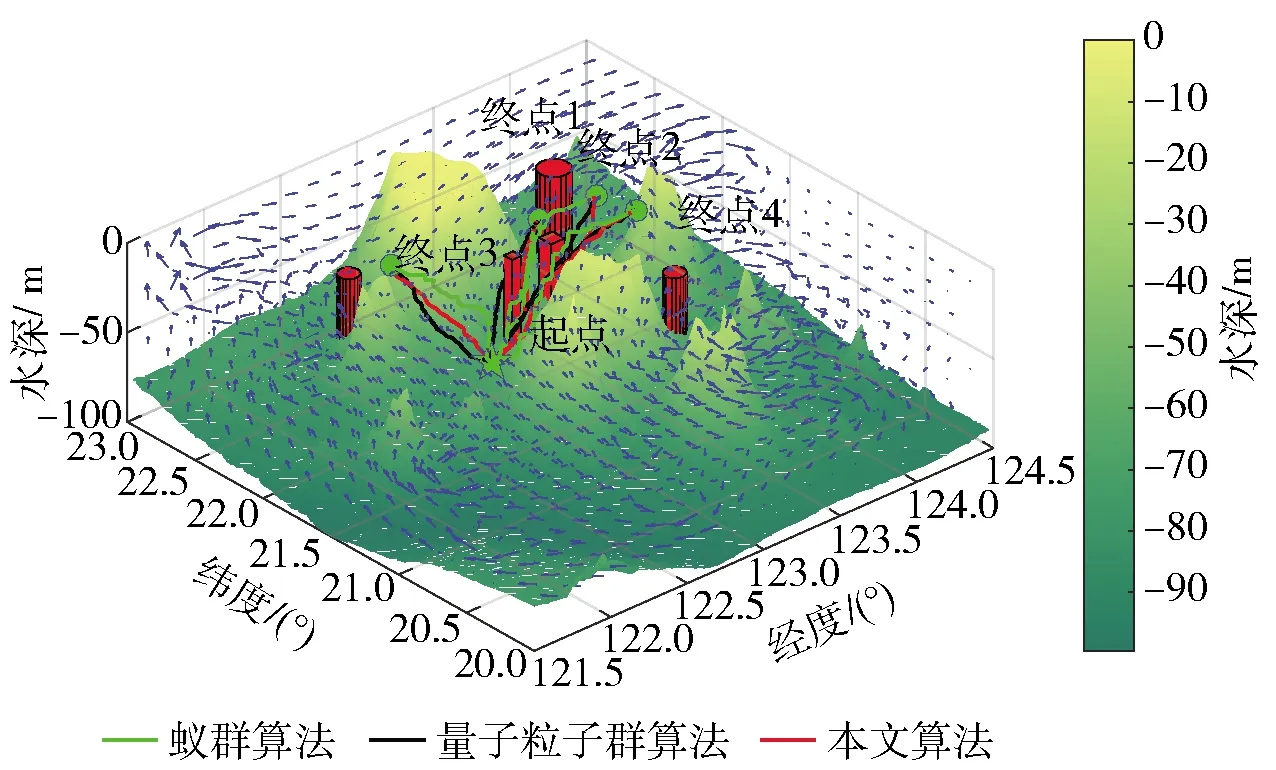

3.2 真实海流下的仿真验证





4 结论

