一类无穷小量的等价性

成凯歌

(浙江旅游职业学院 基础部，浙江 杭州 311231)

“极限”是数学中的分支——微积分的基础概念，微积分的严格化过程是伴随着极限思想的完善过程得以实现的。18世纪，罗宾斯、达朗贝尔与罗依里埃等人先后明确地表示必须将极限作为微积分的基础概念，并且都对极限建立了各自的定义，但他们的定义都无法摆脱对几何直观的依赖。到了19世纪，法国数学家柯西在前人工作的基础上，比较完整地阐述了“极限概念”及其理论，柯西把无穷小视为“以0为极限的变量”，这就正确地确立了“无穷小”概念，从而实现了极限理论的严格化、完备化。“极限”思想方法，是数学分析乃至整个高等数学必不可少的一种重要方法，也是“高等数学”与在“初等数学”的基础上有承前启后连贯性的、进一步思维的发展。高等数学之所以能解决许多初等数学无法解决的问题，正是由于其采用了“极限”的“无限逼近”的思想方法，得到无比精确的计算结果。极限概念本质上就是无穷小的概念，对无穷小量的讨论一直很多[1-13]，本文将对一类等价无穷小量进行探讨。

1 有关概念及结论

定义1[14]设函数f(x)在x0某个空心邻域Uo(x0)上有定义,a为一常数。如果对任意ε>0，都存在δ>0，当x∈Uo(x0,δ)时，有|f(x)-a|<ε，则称当x趋向于x0时，f(x)以a为极限，记作

或者记作

f(x)→a(x→x0)。

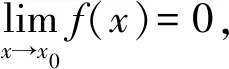
定义3[14]设当x趋向于x0时，f(x)和g(x)都是无穷小量，则

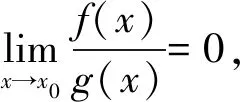
f(x)=o(g(x))(x→x0)，

特别地，当x趋向于x0时，f(x)是无穷小量，记作

f(x)=o(1)(x→x0)。

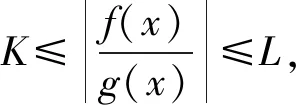
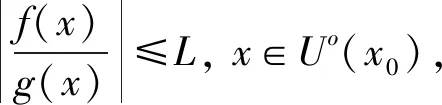
f(x)=o(g(x))(x→x0)，

特别地，若f(x)在某Uo(x0)内有界，则记作

f(x)=o(1)(x→x0)。

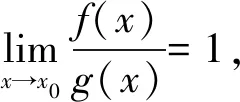
f(x)～g(x)(x→x0)。

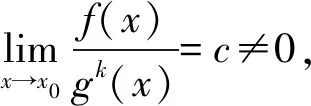
定理1[14]设函数f(x)在x0某个空心邻域Uo(x0)上有定义,则当x趋向于x0时，f(x)以a为极限当且仅当x趋向于x0时，f(x)-a是无穷小量。

定理2[14]1)有限个(相同类型)的无穷小量的和、差、积仍为无穷小量；

2)有界量和无穷小量的积是无穷小量。

定理3[14]设函数f(x),g(x),h(x)在x0某个空心邻域Uo(x0)上有定义，且有f(x)～g(x)(x→x0)，则

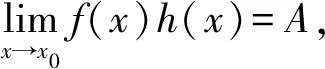
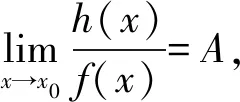
2 讨论过程

在已有的结论基础上，以下进一步讨论无穷小量及其等价关系。

定理4设f(x)=o(g(x))(x→x0)，则对一切正整数n，有g(x)±fn(x)～g(x)(x→x0)。

证明由已知条件得

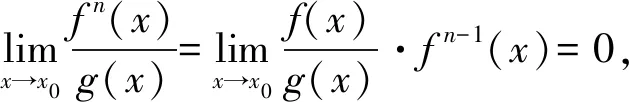
从而

所以，g(x)±fn(x)～g(x)(x→x0)。

定理5设函数f(x)在点x0存在直到n阶的导数，且存在正整数n0使得f(n0)(x0)≠0，则

1)当n0=1时，有f(x)-f(x0)～f′(x0)(x-x0)(x→x0)；

2)当1

证明若函数f(x)在点x0存在直到n阶的导数，则由f(x)在x0处的泰勒公式得

在1)的条件下，有

因此，有

从而f(x)-f(x0)～f′(x0)(x-x0)(x→x0)成立。

在2)的条件下，有

因此，有

从而

成立。

定理6假设函数f(x),g(x),u(x),v(x)满足如下条件：1)f(x)～g(x)(x→0)；2)u(x)～v(x)(x→x0)；3)g(x)在x=0处可导，且g′(0)≠0，则有f(u(x))～g(v(x))(x→x0)。

证明由条件1)得g(x)在x→0时是无穷小量，由条件(3)可得g(x)在x=0处连续，所以，g(0)=0，再注意到可导性，有

g(x)=g(0)+g′(0)x+o(x)(x→0)=g′(0)x+o(x)(x→0)。

g(u(x))=g′(0)u(x)+o(u(x))，

g(v(x))=g′(0)v(x)+o(v(x))。

于是，

结合条件1)，有

因此，结论f(u(x))～g(v(x))(x→x0)成立。

对于g(x)在x=0处可导，且g′(0)=0时将有何种结论？以下定理讨论在g(x)为一类具有这种性质时所具有的结论。

证明由条件1)和3)可设

g2(x)=a0xn+a1xn-1+…+akxn-k，

再利用条件1)，有

因此，结论f(u(x))～g(v(x))(x→x0)成立。

推论1假设函数f(x),g(x),u(x),v(x)满足条件：1)f(x)～g(x)(x→0)；2)u(x)～v(x)(x→x0)；3)g(x)是关于x的多项式，则有f(u(x))～g(v(x))(x→x0)。

推论2假设函数f(x),u(x),v(x)满足条件：1)f(x)～x(x→0)；2)u(x)～v(x)(x→x0)，则有f(u(x))～v(x)(x→x0)。