基于积分泄漏的机电伺服系统摩擦力补偿

朴敏楠，王科磊，孙明玮，黄建，陈增强

(1.南开大学人工智能学院，天津，300350；2.北京自动化控制设备研究所，北京，100074)

所有机电伺服系统中都存在摩擦力，受摩擦力影响，系统位置输出会产生静差、平顶、极限环和低速爬行等现象[1]。为了提高控制精度，设计简单高效的摩擦力补偿方法具有十分重要的意义。已有的摩擦力补偿方法可以分为有模型补偿(基于摩擦力模型)和无模型补偿两大类。有模型补偿需要通过离线或者在线辨识的方法对摩擦力进行建模。工程上常常采用离线辨识和前馈补偿的方法。在理论研究方面，为了适应时变的摩擦力，通常采用自适应参数化模型、神经网络模型或者混合模型，结合自适应控制方法对摩擦力进行实时补偿[2-10]。基于摩擦力模型的补偿方法需要信噪比较高的速度信号。因此，对于速度测量信号信噪比低的系统(没有安装速度传感器且位置传感器的信噪比较低)，无模型补偿成为工程中最普遍的方法[11-17]，其中，PD(proportional derivative)控制是无模型方法中最常用的方法。为了减小摩擦力造成的跟踪误差，通常需要设计高增益PD控制器。由于高增益控制会降低系统对高频未建模动态的鲁棒性以及增大对噪声的敏感程度，因此，在鲁棒性要求下PD 控制能够取得的跟踪精度较低[2]。当PD 控制无法取得期望的跟踪精度时，需要加入积分控制作用。ARMSTRONG 等[18]通过精确的代数方法证明了当同时存在静摩擦和库仑摩擦时，任何可以使系统稳定的PID控制参数组合都会产生极限环。系统在出现极限环震荡时，从静止状态到滑动状态需要克服较大的静摩擦力，瞬时电流很大，电流处于震荡状态，长时间运行会损耗电机。此外，伺服环的震荡会进一步导致外环震荡，例如控制舵面(飞行器的执行机构)的极限环震荡会进一步引发姿态的极限环震荡，从而影响飞行安全。因此，为了保证在提高控制精度的同时能够消除极限环，对积分控制作用进行非线性改造在工程实际中是非常必要的。例如，在积分项上加上误差死区或者设计一些逻辑策略[1,11]，这些方法通常需要进行大量的实验来获取合适的死区参数或者逻辑策略参数， 缺乏严格的理论分析。KESARKAR 等[15]采用分数阶PID 控制和描述函数分析方法降低极限环的幅值，但是由于分数阶积分同样具有低频增益无穷大的特点，该方法不能本质上消除极限环。RANTZER[16]提出在积分控制中加入泄漏项，这样不仅能够提供类积分形式的补偿作用而且能够消除极限环。使用积分二次约束分析方法计算了不产生极限环的泄漏范围。该方法能够对极限环抑制进行严格的理论分析，但只能够计算出最小泄漏的范围，最小泄漏的精确值只能通过反复尝试得到，不便于实际应用。在此基础上，JEON[17]通过分析极限环状态轨迹的代数属性以及利用二分法能够精确求解出不产生极限环的最小泄漏，这种精确的数值求解可以避免反复的仿真和实验尝试，但给出的定理仅考虑了伺服系统闭环极点为3个互异实极点和1个实极点与1对共轭复极点的情况，没有考虑更多闭环极点情形，限制了其在实际中其他闭环极点情形下的应用。而且RANTZER 等[16-17]仅通过数值仿真对理论计算结果进行了验证，并没有进行实验验证。在此，本文作者考虑更多闭环极点情况下最小泄漏的计算，包括三重实极点以及二重实极点情形(包括2 种情况)，并基于严格的数学分析给出这3种情形下最小泄漏的求解方法，通过数值仿真验证计算结果的正确性。最后，在伺服电机平台上进行实验，进一步验证了计算结果的有效性。

1 电机与摩擦力模型

采用伺服电机系统说明设计过程和进行实验验证。该电机属于无刷直流电机，其简化数学模型为

式中：θ为舵机输出位置；ω为电机输出转速；I，L和R分别为电枢电流、电感和电阻；J为转子转动惯量；Ff和Fl分别为摩擦力和外部负载力矩；u为电机的脉宽调制(PWM)输入；ky，kt，ke和ku分别为传动装置减速比、力矩系数、反电动势系数和直流电压。研究在空载状态下进行，因此Fl= 0。

由于电流环的时间常数远比速度环和位置环的小，式(1)可进一步降阶简化为二阶模型：

式中：d1，d2和b为降阶模型的参数，可以通过实验数据进行参数辨识得到。本文中考虑的非线性摩擦力模型如下：

式中：Fc为库仑摩擦力；ρ为最大静摩擦力Fs大于库仑摩擦力的倍数。当外力小于等于最大静摩擦力时，静摩擦力能够完全抵消外力作用且物体保持静止。当外力大于最大静摩擦力时，物体开始运动且受到与物体运动方向相反的库仑摩擦力作用。该模型只考虑了静摩擦力和库仑摩擦力，黏性摩擦力可以包含在模型参数d2中。现实中，摩擦力模型精细、复杂，例如从克服最大静摩擦力开始滑动到摩擦力降到库仑摩擦力水平之间存在Stribeck效应的过渡过程。此外，还有考虑摩擦力动态特性的一些动态模型，例如LuGre 模型。HENSEN等[19]得出了LuGre模型和式(3)模型极限环的定性和定量分析结果都基本一致的结论。因此，对于极限环分析来说，式(3)模型已经足够。

2 基于积分泄漏的控制策略

带积分泄漏的PID控制律的形式[16]为

式中：e=θd-θ，为位置误差信号；θd为位置指令；ξ为误差积分的替代值；γ为积分泄漏；kp和kd分别为比例和微分控制系数；ki为状态ξ的增益。e到ξ之间的传递函数为ξ/e= 1/(s+γ)，其中，s为复变量。可以看出：当γ= 0 时，该控制器就为传统的PID控制。通过加入泄漏将纯积分环节变为一阶惯性环节，避免了在误差低频处增益无穷大。为了便于分析，将式(2)中的模型参数同时除以Fc得到

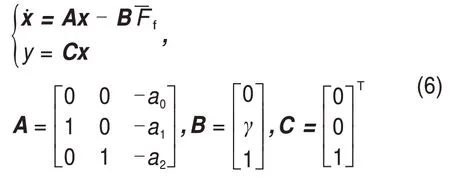
式中：a0，a1和a2为能观标准型中的参数，x=[x1x2x3]T，为状态向量。各状态和真实物理状态之间的关系为

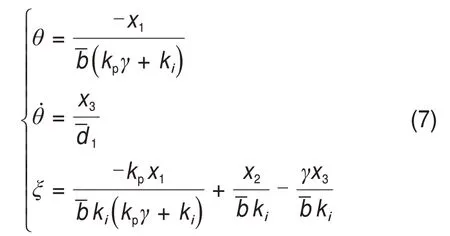
其中，αi(i= 1,2,3)为状态迁移矩阵的元素，第1列和第2列元素之间存在导数关系，这是因为A是能观标准型下的状态矩阵。第3列元素在以下的分析中没有用到，因此没有具体列出。ARMSTRONG等[18]证明当系统存在静摩擦力时(ρ> 0)，所有使系统稳定的PID 控制参数(γ= 0)都一定会产生极限环。

3 最小积分泄漏的数值求解方法

采用文献[17]中的方法计算极限环幅值和最小积分泄漏时需要用到以下重要定理。

定理1[17]：设A的特征根为λi(i= 1,2,3)。当λi全部为实数时，有λ3<λ2<λ1< 0；当λi中有1对复数时，有λ2,3=σ±ϖj(σ< 0)。对于给定的静摩擦力水平ρ> 0，能够消除系统(6)极限环的最小积分泄漏γ> 0可以通过式(9)求解：

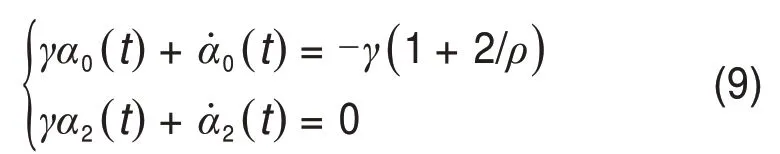
其中，解γ∗一定位于区间γ∗∈(0,-λ1)。令η=-γ*/λ1，则t∗一定位于区间t∗∈(0,tη)，其中tη为t∗的上界值。当A的特征根为互异实数时，

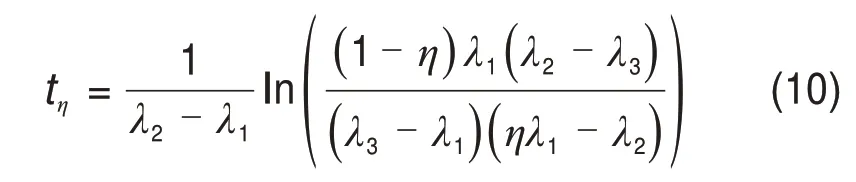
当A的特征根存在1对复数时，

式(9)为超越方程组，难以对其进行直接求解。因此，可以首先确定γ∗和t∗的范围，然后采用双环二分法在范围内搜索γ∗和t∗的精确值。显然，定理1 仅考虑了闭环极点的2 种可能形式。本文考虑了闭环极点的更多可能情形，包括三重实根和二重实根(包含2种情形)共3种情形，并给出定理2。

定理2：设A的特征根为λi(i= 1,2,3)。当λi为三重实数时，有λ3=λ2=λ1< 0；当λi中有1对重根时，有λ3<λ2=λ1< 0 或λ3=λ2<λ1< 0。对于给定的静摩擦力水平ρ> 0，能够消除系统(6)极限环的最小积分泄漏γ> 0可以通过式(12)求解

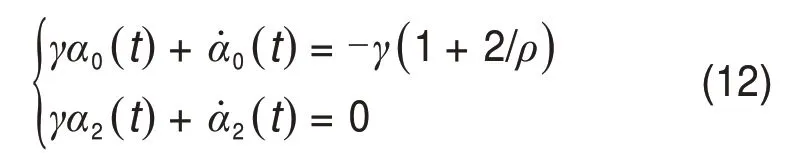
式中：解γ∗一定位于区间γ∗∈(0,-λ1)。令η=-γ*/λ1，则t∗一定位于区间t∗∈(0,tη)。当A的特征根为三重实根时，t∗可以唯一地确定为

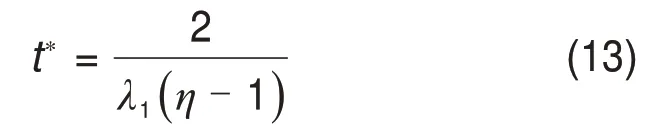
当A的特征根λ3<λ2=λ1< 0时，

当A的特征根λ3=λ2<λ1< 0时，

证明：

1)当A的特征根为三重实根时，α2=t2eλ1t/2。容易证明得到

即-α̇2/α2在t> 0 上从负无穷单调递增到-λ1。由式(12)中第2式可知γ=-α̇2/α2。由于γ> 0，因此γ的解区间应在(0,-λ1)。设η= -γ*/λ1，则根据可以解出对应于γ*的唯一时间解为t∗=下面证明γ∗∈(0,-λ1)同样也是式(12)中第1式的解区间。由于

可以得到

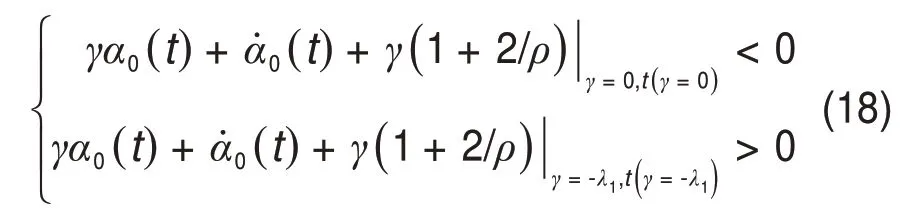
因此，得到γ∗∈(0,-λ1)为同时满足式(12)中两式的解区间。

2)当A的特征根λ3<λ2=λ1< 0时，

经过数学计算可以得到

因 此，γ*的解区间应在(0,-λ1)。 设η= -γ*/λ1，此时对应于γ*的唯一时间解t(γ∗)不存在解析解，因此，先计算出t(γ∗)的可行范围。将式(14)代入-ηλ1α2(t)+α̇2(t)得到

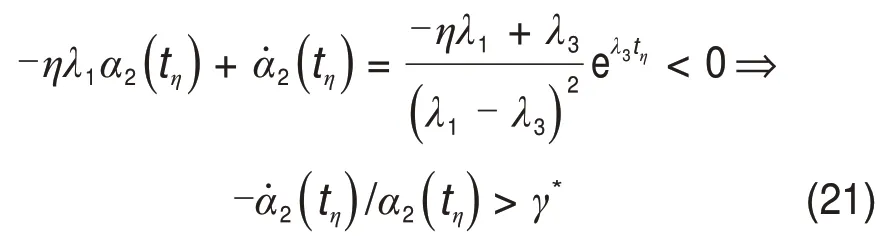
由式(22)同样可以得到式(18)中的结果。因此，可以得到γ∗∈(0,-λ1)为同时满足式(12)中两式的解区间。

3)当A的特征根为λ3=λ2<λ1< 0时，

经过数学计算同样可以得到式(16)中的结果。因此，γ的解区间应在(0,-λ1)。设η=-γ*/λ1，此时，对应于γ*的唯一时间解t(γ∗)不存在解析解。因此，可先计算出t(γ∗)的可行范围。同式(21)，需要找到1个tη使其满足

式(24)等效为

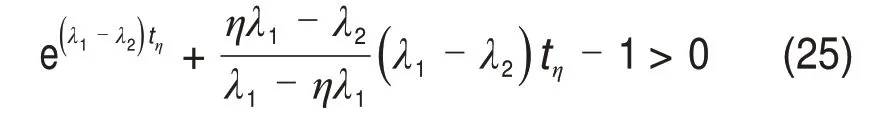
其中：

且有

综合式(26)和式(27)可以得到

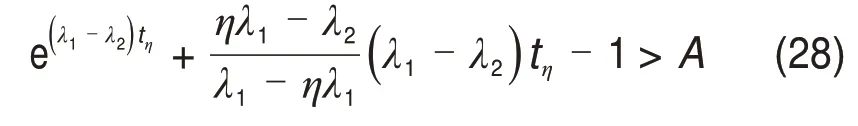
式中：

令A= 0 可以得到式(15)，此时，求解的tη能够使得式(24)成立。因此，(0,tη)区间包含对应于γ*的唯一解，证明过程与式(17)和式(18)的证明过程相同。因此，得到γ∗∈(0,-λ1)为同时满足式(12)中两式的解区间。

证毕。

在获得γ和t的解区间后即可在解区间内采用双环二分法搜索得到γ∗和t∗的精确值。双环二分法的具体执行步骤如下[17]。

步骤1)：进行参数初始化，令γu= -λ1，tu=tη，γl=tl=γ=t= 0，ε0=ε2= 1× 10-8，f0=f2= 1。其中，f0=γα0(t)+α̇0(t)+γ(1+ 2/ρ)；f2=γα2(t)+(t)；γu和γl分别表示γ的上下界变量；tu和tl分别表示t的上下界变量；ε0和ε2分别表示外环和内环二分法的终止精度。

步骤2)：进行如下双环迭代求解计算。

步骤3)：迭代求解结束即可得到满足精度要求的最小泄漏γ*=γ。

在求出γ*之后需要对原有的比例系数、积分系数和微分系数进行调整以保证闭环极点保持不变。调整后的控制参数如下：

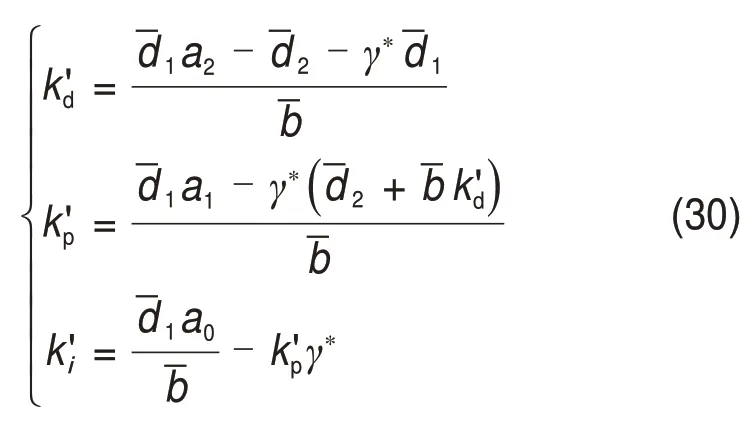
为了进一步求解极限环幅值，有如下引理。

引理1：对于给定的积分泄漏γ> 0 和静摩擦力水平ρ> 0，若系统(6)存在稳定的极限环，则极限环的幅值可由式(31)计算得到：

证明：式(31)可以由文献[17]中的推论1 直接得到。解区间的证明过程和定理2完全相同。结合式 (7)和即可得到θ∗=

证毕。

4 仿真结果与分析

采用文献[17]中的对象，考虑定理2 针对的3种情形。3 种情形下闭环极点的配置分别为(λ1=λ2=λ3= -5)， (λ1=λ2= -4,λ3= -7)和 (λ1=-4,λ2=λ3= -7)，分别称为情形1、情形2 和情形3。根据定理2 确定的求解范围以及二分法可以精确计算最小泄漏γ*。在每种情形下，有略小于和略大于γ*的2 个值γl和γh，其对应的极限环幅值仿真结果分别为θl和θh，理论计算结果分别为θl∗和。为了能够精准地对不连续摩擦力进行仿真，数值计算方法选为变步长的ode23 Bogacki-Shampine。3种情形下的理论计算结果和仿真结果如表1所示，仿真结果如图1～6所示，图中，θ为角度输出，U为控制电压。从图1～6 可以看出，当γ=γl时，系统中存在极限环，且极限环幅值的仿真结果和理论计算结果基本相同；当γ=γh时，系统中极限环消失。γl，γh和γ∗基本相同，这说明了最小泄漏理论计算结果的精确性。随着γ的变化极限环的吸引域也在发生变化。现在对极限环吸引域的计算还没有精确的方法。通过数值仿真发现：随着γ变大吸引域逐渐变小。当γ= 0 时，吸引域无穷大；当γ<γ∗且γ无限接近γ∗时，吸引域趋近于一点；当γ>γ∗时，极限环完全消失。

表1 理论计算和数值仿真结果比较Table 1 Comparison of results for theoretical calculation and numerical simulation

为了验证该文模型与算法的优势，本文选择另一种接近工程实际的无模型控制方法——自抗扰控制(ADRC,active disturbance rejection control)[20]作为对比算法。该控制方法由PID控制基础上改进得来，ADRC 的核心为扩张状态观测器(ESO，extended state observer)。为了与PID 控制进行对比以及进行最小积分泄漏计算，针对式(2)中对象设计一阶线性ADRC 以保持与PID 控制器阶次相同。首先，将式(2)中对象改写为

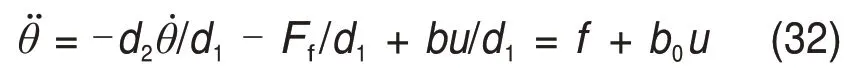
图1 极点情形1下γ = γl的仿真结果Fig.1 Simulation results for γ = γl under case 1

图2 极点情形1下γ = γh的仿真结果Fig.2 Simulation results for γ = γh under case 1

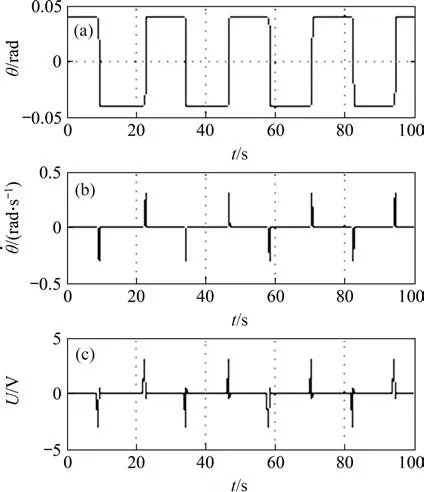
图3 极点情形2下γ = γl的仿真结果Fig.3 Simulation results for γ = γl under case 2

图4 极点情形2下γ = γh的仿真结果Fig.4 Simulation results for γ = γh under case 2

式中：ωo为观测器增益，其决定总扰动的估计速度。在得到总扰动估计后可以设计如下控制律：

图5 极点情形3下γ = γl的仿真结果Fig.5 Simulation results for γ = γl under case 3

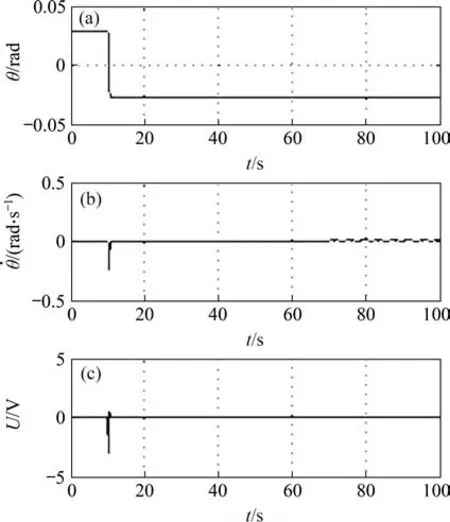
图6 极点情形3下γ = γh的仿真结果Fig.6 Simulation results for γ = γh under case 3

式中：kp′和kd′分别为比例和微分增益。通过将式(34)和式(35)进行拉式变换可以得到控制律的等效形式

从式(36)可以看出：该控制律的等效形式即为PID控制加上1项位置反馈，从而改善系统的动态响应，缓解PID控制中响应速度和超调量之间的矛盾。在进行极限环分析时，可以将指令θd= 0，则式(36)可以写为PID形式：

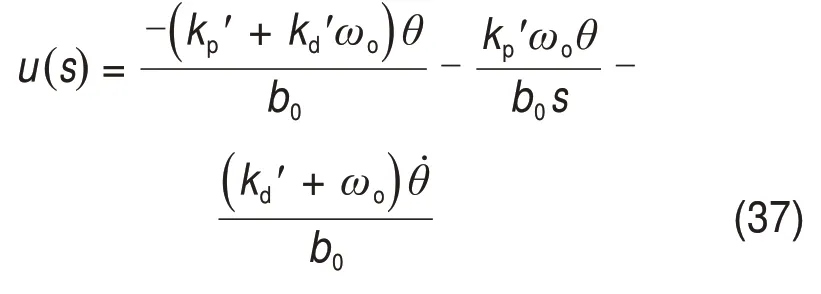
由文献[18]可知，针对同时带有静摩擦和库仑摩擦的二阶系统(2)，任何使系统稳定的一阶ADRC参数都会使系统产生极限环。由于产生极限环的根本原因在于积分项，因此，可以在式(37)中的积分项上加上适当泄漏，并按照本文的方法计算出最小积分泄漏。此时，带有积分泄漏的一阶自抗扰控制律变为

为了进行对比，设计ADRC 的控制参数使得闭环系统的极点与上述3种情形下PID控制的闭环极点相同。当指令为0时，积分泄漏型PID和积分泄漏型ADRC完全一致，但是当指令不为0时，积分泄漏型ADRC 会由于额外的位置反馈项具有不同的特性。相较于积分泄漏型PID，积分泄漏型ADRC的主要问题是会产生较大的稳态误差。在θd分别为5 rad 和10 rad、不产生极限环条件下(γ取值为表1中的γh)，2种方法的稳态误差如表2所示。从表2可以看出：积分泄漏型ADRC具有较大的稳态误差，且稳态误差受指令影响。积分泄漏型PID虽然也具有一定的稳态误差，但是其值比较小。为了对这一结果进行解释，可以计算不考虑摩擦力时积分泄漏型ADRC的闭环传递函数：

式中：

表2 2种积分泄漏型算法稳态误差比较Table 2 Comparison of two types of integrator leakage algorithms in terms of steady error

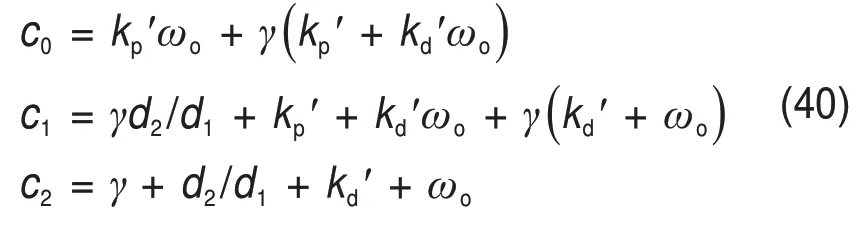
从而可以得到闭环稳态增益为

从式(41)可以看出：当ωo= 0 时(积分泄漏型PID)，稳态增益为1；当ωo≠0 时(积分泄漏型ADRC)，稳态增益小于1，且稳态增益与kd′ωo成反比。因此，积分泄漏型ADRC 在存在摩擦力时相较于积分泄漏型PID会具有更大的静差。综合上述可知，积分泄漏更适用于加在PID控制器上。

5 实验结果与分析

实验平台的电机为直流无刷电机，是一类飞行器的伺服机构，又称为舵机。该电机通过驱动舵面的偏转控制飞行器的姿态。电机的运动参数如下：ky=1/280，kt=0.19 N·m/A，ke＝24 mV·s/(°)，ku=100 V，J=0.05g·m2，R=0.36 Ω，L=2.8 mH。实验平台处理器为ARM STM32F427，采用C语言编写控制算法，控制周期为0.25 ms，位置信号由电位器测量，仅对舵机系统中的1 个舵机进行实验。为了计算最小泄漏，首先需要辨识舵机模型(2)的参数。舵机在不同速度下匀速运动，实际控制电压U=kuu和舵机速度之间的关系如图7所示。由于电机参数存在误差，采用辨识的方法得到电机的二阶动态模型(2)。通过辨识可以近似得到Fc= 0.48 V，Fs= 0.74 V，ρ= 0.54。令模型(2)中d1= 1，利用舵机在滑动运动过程中的输入输出数据(仅需考虑库仑摩擦力，黏性摩擦力的影响反映在系数d2中)可以辨识出d2= 97.96，b= 37 606。

图7 电机的实验摩擦力(以等效控制电压)曲线Fig.7 Experimental friction(represented by equivalent control voltage)curve of motor

考虑到动态性能、鲁棒性能以及摩擦力补偿速度，将PID 参数设计为kp= 50，kd= 0.1，ki=300，此时，开环截频6.2 Hz，相位裕度64°，闭环极点为λ1= -7.27，λ2,3= -49.45- 30.67i。利用定理1 可以计算得到γ*= 0.721。为验证理论计算结果的正确性，令γ分别为0.73 和0.75。当γ= 0.73时，调整PID参数保持闭环极点不变，此时，kp=49.06，kd= 0.09，ki= 264.18；当γ= 0.75 时，调整PID参数保持闭环极点不变，此时，kp= 49.04，kd= 0.09，ki= 263.22。γ= 0.73 和γ= 0.75 时的实验结果分别如图8 和图9 所示。位置指令设定为0.1°，0.2°，0.3°和0.4°的阶跃信号，幅值为0.5°、频率为0.1Hz 的正弦信号以及0.01°/s 的斜坡信号。从图8 可以看出：当执行从0.6°到1.0°的定点任务时，出现了极限环震荡。从图9可以看出：阶跃跟踪时的极限环已经完全消失，在位置回归到零位时虽然出现了短暂的震荡，但是最终还是收敛到0。在跟踪阶跃指令时，存在0.01°的静差。静差是加入积分泄漏造成的，但仍然满足跟踪精度要求。在跟踪低速正弦指令时，跟踪精度很高，平顶时间很短。同样，在跟踪低速斜坡指令时，没有极限环和爬行运动产生。需要说明的是，加入积分泄漏只会减小回路传递函数在低频处的增益，对截频和相位裕度几乎没有影响，因此不会影响系统的鲁棒性。

图8 γ = 0.73时的实验结果Fig.8 Experimental results for γ = 0.73

图9 γ = 0.75时的实验结果Fig.9 Experimental results for γ = 0.75

根据理论计算结果，当γ= 0.73时，极限环应该完全消失，但在实验中，γ= 0.75时极限环才完全消失，这个偏差是由舵机的线性动态和摩擦力的建模误差造成的。但理论计算结果和实验结果之间的偏差非常小，这说明了理论计算能够为实际γ的取值提供比较准确的参考。该方法通过在传统PID控制上进行简单的线性改造，在不降低鲁棒性的前提下，不仅能够快速地补偿摩擦力，还能够完全消除极限环，具有一定的实际工程价值。

6 结论

1)采用带有积分泄漏的PID 控制方法解决机电伺服系统摩擦力补偿的极限环问题，给出了能够消除极限环的最小积分泄漏的计算方法，数值仿真结果验证了计算方法的准确性。

2)与带有积分泄漏的自抗扰控制方法相比，带有积分泄漏的PID控制能够取得更小的静差。

3)在伺服电机实验平台所得的实验结果与理论计算结果基本一致，说明理论计算能够为实际泄漏的选取提供较准确的参考，具有一定的实际工程价值。