似然K均值聚类用于涡扇发动机气路故障诊断

卢俊杰，黄金泉，鲁 峰

南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京210016

1 引言

随着现代航空工业的不断发展，航空发动机的性能也越来越高，但由于其日益复杂的结构设计，各种故障的发生率也在不断上升。相比于其他机械设备，航空发动机有着故障量高、调整复杂、维护量大的特点[1]，相关统计资料表明，航空发动机故障引起的飞行事故占比高达40%以上[2]。因此，航空发动机故障诊断方法的研究尤为重要。由于工作负荷大、工作状态切换频繁、工作环境恶劣等特性，航空发动机的故障机制和故障表现也呈现复杂化、多样化的特点[3]。为了提高航空发动机的飞行安全性以及降低维护成本，国内外相关研究机构一直将及时、准确、高效地进行航空发动机故障诊断作为研究的重点与热点。航空发动机的气路系统是发动机的核心系统，气路系统故障一般分为部件故障和传感器故障[4]。根据测量到的气路参数对气路系统进行故障诊断，快速且准确地实现故障定位，对于提高发动机安全性与可靠性，由定期维修转变为视情维修，以降低维护费用有巨大的技术支持[5]。

模式识别是航空发动机气路故障诊断的主要内容之一，即根据数学方法对含有故障信息的数据自动进行处理和识别，提取有效的诊断规则，从而对故障样本进行聚类或者分类[6]。通过监测与采集反映发动机运行状态的信号，并进行处理，然后根据模式识别方法对数据之中蕴含的能够反映气路系统运行状态的特征信息进行辨识，从而可以判断出航空发动机气路系统的运行状态。如果发生了气路故障，则可以对故障类别与部位等信息进行判断，为维修决策提供指导。在航空发动机故障诊断领域，模式识别方法得到了广泛的研究，主要分为有监督和无监督的方法。有监督的方法主要有神经网络、支持向量机、贝叶斯分类和决策树等[7]。曹惠玲[8]将支持向量机应用于机械故障诊断中，但支持向量机需要先标记训练样本并进行迭代训练，计算时间较长。刘永建[9]运用改进的神经网络对发动机故障进行诊断，但神经网络易于陷入局部最优解，并且网络训练时间过长。徐宾刚等人[10]提出了在故障信号不完整情况下基于贝叶斯方法的转子故障推理诊断。这些有监督的方法需要通过对训练样本的学习才能在测试集上实现较为准确的分类，并且需要提前指定训练样本的标签信息[11]，另外分类的准确率很大程度上受训练样本规模、分布等影响。

模式识别的另一重要分支就是无监督的聚类，即在一种特定相似度量的基础上对数据进行划分的过程，其被广泛应用于市场分析、人脸识别、信息安全等方面[12]。在聚类过程中没有任何关于数据结构或者标签的先验知识，通过提取样本特征数据相似程度信息，使同一聚类的样本尽可能相似，以及不同聚类的样本尽可能相异。近年来各种聚类方法在航空发动机故障诊断中也得到了较多应用。Liu 等人[13]提出了一种基于K 均值聚类的航空发动机数据处理方法，取得了良好的效果。邓贝贝[14]通过小波聚类算法进行航空发动机的故障诊断，验证了该方法在航空发动机转子系统故障诊断中的优越性。刘建勋[15]提出一种利用征兆与故障间的模糊性关系的模糊C 均值聚类算法，对航空发动机转子部件故障进行了诊断。K 均值聚类是应用最广泛的聚类方法，通过不断迭代求解各聚类中心，在凸性数据集上往往能够达到很好的效果[16]。但是K 均值聚类算法不能有效应用样本特征离散程度信息，导致聚类边缘样本容易被误聚类。

针对传统K 均值聚类算法的不足，本文提出了似然K 均值聚类算法，通过考虑样本每一维特征的离散程度信息，分别计算样本属于某一聚类的似然概率，有效提高了K 均值聚类算法的准确率。并将似然K 均值聚类算法应用于涡扇发动机气路部件故障以及传感器故障的模式识别，验证了该算法在涡扇发动机故障模式识别中的实用性和有效性。

2 K均值聚类及改进

聚类过程就是指将相似对象聚集成同一组或者同一类的过程，目的是使聚类内部尽可能紧凑，不同类类间尽可能分开。为此，MacQueen 提出了K 均值聚类方法[17]，本章回顾传统的K 均值聚类算法，并针对其不足提出似然K 均值聚类算法。

2.1 K均值聚类

随机选取k 个初始聚类中心后，K-means 的主要过程为交替进行样本集合的更新与聚类中心的更新。

样本集合更新即根据最小欧式距离准则，将每个样本聚类到最近的聚类中心，其更新公式为：

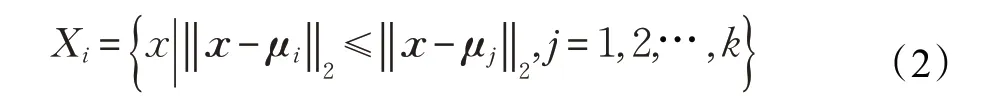
假设第i类样本Xi的聚类中心为μi，Xi中样本数目为ni，则聚类中心的更新公式为：

不断重复以上的交替更新过程，直到标准测度函数收敛，一般采用均方差作为聚类测度函数，其形式为：

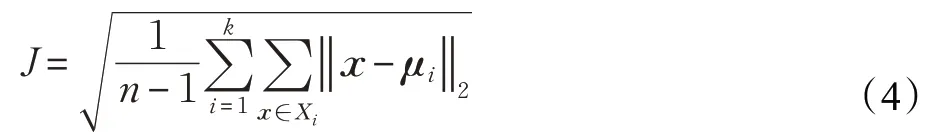
一般而言，J 能够反映类中样本围绕聚类中心的紧密程度，较小的J 通常能够表明类中样本具有较高的相似性。

K 均值聚类算法是被广泛研究与应用的聚类算法，在凸性聚类问题中往往有较好的效果。但是由于未能考虑样本特征离散程度信息，导致聚类边缘样本容易误分类，且算法易于陷入局部最优解，聚类准确率较低。

给定所有样本集合X 及类别数k，K 均值聚类算法如下：

步骤1 采用轮盘赌算法，在整个样本集X 中随机选取k个样本作为初始聚类中心

步骤2 对于每个样本x，分别计算其到k 个聚类中心的欧式距离

步骤3 根据式（2）更新样本集合

步骤4 根据式（3）更新聚类中心

步骤5 判断式（4）中的测度函数J 是否收敛，若未收敛且未到最大迭代次数，则转至步骤2。否则结束算法，k个样本集合则为聚类结果。

2.2 似然K均值聚类

在传统K 均值聚类算法中，样本集合的更新完全按照最小欧式距离的原则来进行，每个聚类中心的影响力被认为是平等的，样本特征更靠近哪个聚类中心便被归为该类。但实际问题中不同类别的特征数据往往有不同的离散程度，此时传统K均值聚类方法中的样本集合更新方式则不合理，例如在图1 所表示的平面二分类聚类问题中，第一类的聚类中心为μ1=(0.9,0.9)，第二类的聚类中心为μ2=(-1,-1)，假设存在样本x=(0,0)，按照传统K 均值聚类的准则，则样本x 应该被归为聚类中心更近的第一类。观察图中两个维度特征的分布情况，样本x 显然应该归入第二类。由于K 均值聚类未考虑样本特征的离散程度，在不同聚类的样本特征离散程度差异较大时，K 均值聚类方法的聚类准确率较低。

图1 平面二分类聚类问题

针对K 均值聚类方法不能处理样本特征离散程度的缺点，本文提出了似然K 均值聚类方法，根据样本属于每个类的似然概率来进行样本集合更新。假设第i聚类样本的第j维度特征的方差为σij，其计算如下：

则样本x 属于聚类Xi的似然概率P( x ∈ Xi)可以通过以下两式求取：

按照如下的最大似然概率原则进行样本集合更新：

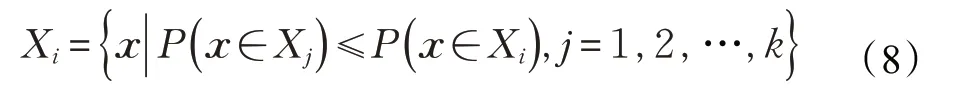
采用如下似然概率误差平方和形式作为似然K 均值聚类算法的概率测度函数，其形式为：

给定所有样本集合X 及类别数k，似然K 均值聚类算法如下：

步骤1 采用轮盘赌算法，在整个样本集X 中随机选取k个样本作为初始聚类中心

步骤2 对于每个样本x，根据式（6）、（7）分别计算其属于k个聚类中心的似然概率

步骤3 根据式（8）更新样本集合

步骤4 根据式（3）更新聚类中心

步骤5 判断式（9）中的测度函数JP是否收敛，若未收敛且未到最大迭代次数，则转至步骤2。否则结束算法，k个样本集合则为聚类结果。

2.3 收敛性及复杂度

根据似然K 均值聚类算法的步骤，对于有n个样本的聚类问题，似然K 均值聚类算法所需的计算量与n成正比，所以其计算复杂度为O(n)，与传统的K 均值聚类算法计算复杂度在同一量级。

3 数据集验证

为验证本文提出的似然K 均值聚类算法在处理样本特征离散程度信息方面的有效性及其相对于传统K均值算法的优越性。本章对似然K 均值聚类及传统K均值聚类算法在两个人造数据集和4 个基准数据集上进行了对比实验。实验的硬件环境为1 台PC 机（CPU主频为2.50 GHz，内存2 GB），软件环境为Matlab7.0。

3.1 人造数据集

为了检验似然K 均值聚类算法是否能够通过利用样本特征离散程度信息来提高聚类准确率，采用随机方式生成具有不同离散程度的三中心聚类数据集和双圆环聚类数据集。图2和图3分别给出了K 均值聚类算法和似然K 均值聚类算法在三中心聚类数据集上的聚类效果。由图2 可以看出，K 均值聚类算法虽然能够大致将样本分为三类，但是由于未能利用样本特征离散程度信息，在靠近聚类边缘部分，有较多明显应该属于第一类和第二类的样本被错误分入了第三类。由图3 可以看出，似然K 均值聚类算法可以很好地将样本分为三簇，聚类边界清晰，几乎没有被错误聚类的样本。对于第一类和第二类中靠近聚类边缘的样本，没有出现被错误分入第三类的情况。

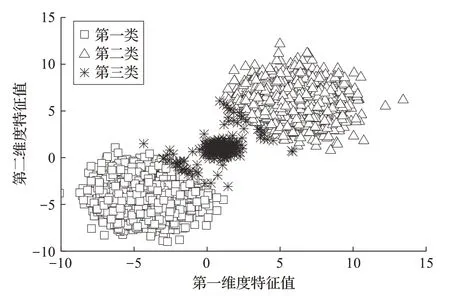
图2 K均值聚类算法在人造三中心聚类数据集上效果

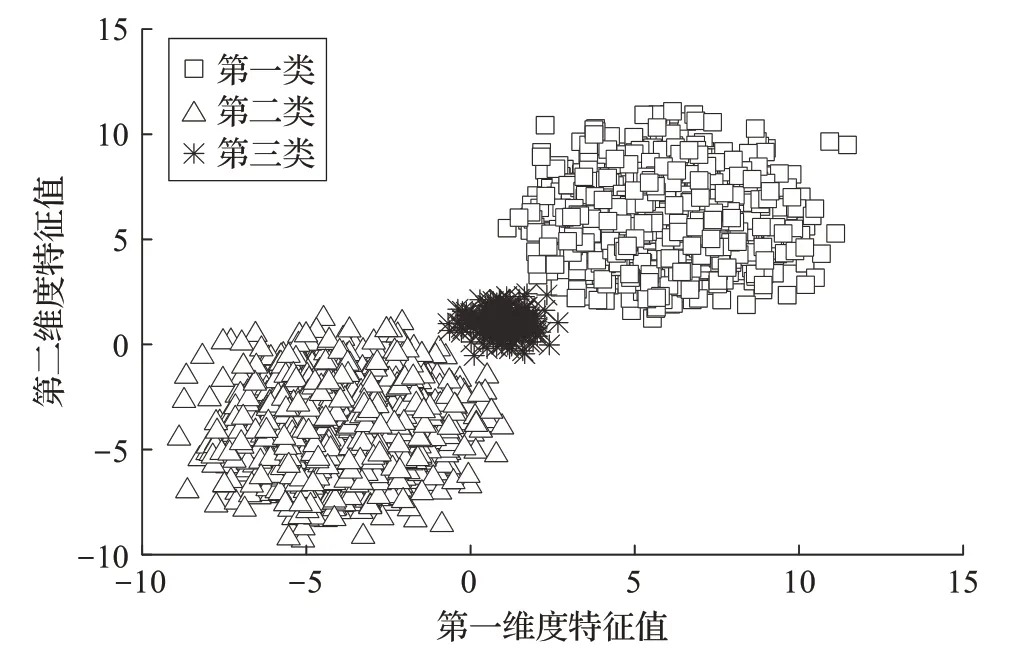
图3 似然K均值聚类算法在人造三中心聚类数据集上效果

图4 和图5分别给出了K 均值聚类算法和似然K 均值聚类算法在双圆环聚类数据集上的聚类效果。由图4可以看出，K 均值聚类算法虽然能够大致将样本聚类为内外圆环，但是由于未能利用样本特征离散程度信息，在靠近聚类边缘部分，有较多明显应该属于第一类的样本被错误分入了第二类。由图5 可以看出，似然K 均值聚类算法可以很好地将样本分为内外两个圆环状簇，聚类边界清晰，几乎没有被错误聚类的样本。对于第一类中靠近聚类边缘的样本，没有出现被错误分入第二类的情况。

图4 K均值聚类算法在人造双圆环聚类数据集上效果

图5 似然K均值聚类算法在人造双圆环聚类数据集上效果

通过这两组人造数据集的验证，可以清晰看出似然K 均值聚类算法在处理具有不同离散程度样本时的优越性，但这两个数据集中样本的不同离散程度是人为设置的，为了进一步验证改进算法的优越性，还需要在更有说服力的真实聚类问题的基准数据集上开展对比实验。

3.2 基准数据集

为验证似然K 均值聚类算法在真实问题中的普适性与优越性，选取了4 个基准聚类数据集进行实验，表1给出了基准数据集的详细信息，包括各数据集的类别数、特征维数、总样本数。Iris、Wine 及Seeds 聚类数据集从UCI下载[18]，Yeast数据集从Mulan数据库下载[19]。

表1 聚类基准数据集详细信息

表2 给出了K 均值方法及似然K 均值方法在基准数据集中性能比较，从表中可以看出，在每一个数据集中，似然K 均值算法的错误聚类数均比K 均值的聚类数要少，因此聚类准确率更高。对于一些样本特征离散程度差距较大的数据集，似然均值聚类算法对聚类准确率的提升效果尤其明显。例如Iris 数据集，图6 给出了在该数据集中两种聚类方法的效果比较，由图中可以看出，似然K 均值算法可以有效地减少误分类点的个数。

表2 两种聚类方法在基准数据集中性能比较

图6 K 均值方法及似然K 均值方法在Iris数据集中聚类效果比较

4 涡扇发动机气路故障诊断

航空发动机是影响飞行安全问题的重要因素，气路系统是航空发动机的核心系统与故障高发系统。通过故障诊断技术，及早发现航空发动机气路系统的故障，对保障飞行安全，降低航空发动机的维护成本，提高航空产业的效益有着重要的意义[20]。本文通过将似然K 均值聚类方法应用到涡扇发动机的气路部件故障和传感器故障的模式识别之中，并对传统K 均值聚类算法所得到的实验结果进行对比，以验证似然K 均值聚类算法在航空发动机异常状态监控中的实用性和有效性。

4.1 旋转部件故障聚类

涡扇发动机气路旋转部件主要有：风扇、压气机和高低压涡轮。假设涡扇发动机的四个旋转部件故障，每个部件均考虑轻度故障以及重度故障两种情况。旋转部件故障程度一般通过效率系数和流量系数使标准部件特性图的变形效果来刻画，每种部件故障情况的平均效率系数以及平均流量系数在表3 中给出。表3 同时给出了K 均值方法及似然K 均值方法在发动机部件故障聚类中性能比较，由表中可以看出，总体而言，似然K 均值方法对各类部件故障的错误聚类数更少，准确率更高。

表3 两种聚类方法在发动机部件故障聚类中性能比较

4.2 传感器故障聚类

涡扇发动机气路主要传感器包括高低压转速传感器和各旋转部件出口截面温度压力传感器，选取10 种故障模式，每种故障模式选取50个聚类样本。图7给出了K 均值方法及似然K 均值方法在发动机传感器故障聚类中效果比较，由图中可以看出，似然K 均值算法可以有效减少误分类点的个数。对于共计500 个聚类样本，K 均值算法的误聚类数为30，似然K 均值算法的误聚类数为11，似然K 均值算法能够有效减少误聚类数，提高聚类准确率。

5 结束语

图7 K均值方法及似然K均值方法在发动机传感器故障聚类中效果比较

本文分析了当前航空发动机气路故障诊断的现状，针对传统K 均值聚类方法不能处理涡扇发动机聚类问题中样本特征离散程度信息的不足，提出了一种以最大似然概率为聚类准则的似然K 均值聚类算法。并在人造数据集上验证了该算法在处理样本特征离散程度信息方面的优越性，在基准聚类数据集上验证了该算法对现实问题的普适性与有效性。最后将其应用在了涡扇发动机气路部件故障和传感器故障的模式识别问题中，有效提高了涡扇发动机气路故障诊断中聚类问题的准确率，对快速有效地实现涡扇发动机异常状态监控有着重要意义。