一道自编试题的解法探究

江西省永修县第一中学 (330304) 易 华

1．试题呈现

已知函数f(x)=ex-mx有两个零点x1,x2，则下面结论正确的是.

本题考查含参函数极值点偏移问题，考查函数零点、二元变量范围问题、主要考查函数与方程思想、数形结合思想、化归转化思想、分类讨论思想，旨在考查学生的逻辑推理、数学运算等核心素养.

2．解法探究

本题是含参函数极值点偏移问题，首先应探究参数的取值范围.

解法1：(分类讨论)因为f′(x)=ex-m.

①若m≤0时,f′(x)>0，f(x)在R上单调递增，不存在两个零点.

综上，当m>e时f(x)有两个零点.

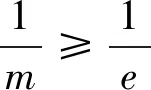
综上，当m>e时f(x)有两个零点.

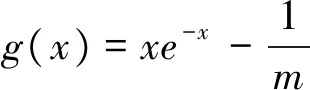
其次，面对双变元的不等式问题，我们的解题策略是转化为单变元的不等式问题进行解答.

对(3)的解法探究：

解法1：(构造函数法)不妨设x12等价于f(x1)>f(2-x2),即f(x2)>f(2-x2).

记g(x)=f(x)-f(2-x)=ex-e2-x+2m(x>lnm)，g′(x)=ex+e2-x>0,故g(x)在(lnm,

解法2：(换元法)令t=x2-x1,

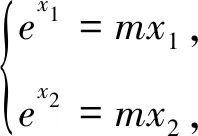
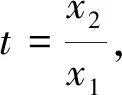
对(4)的解法探究：

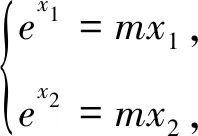
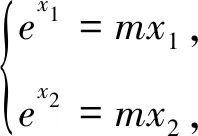
综合上述探究，得出正确结论共有(2)(3)(4).

点评:以上解题方法均是为了实现将双变元的不等式转化为单变元不等式，方法一、四利用构造新的函数来达到消元的目的，方法二、三则是利用构造新的变元，将两个旧的变元都换成新变元来表示，从而达到消元的目的.

3．解法反思

含参数的极值点偏移问题，在原有的两个变元x1,x2的基础上，又多了一个参数，故思路很自然的就会想到：想尽一切办法消去参数，从而转化成不含参数的问题去解决；或者以参数为媒介，构造出一个变元的新的函数.

通过上述解法探究，可知用构造函数法求解极值点偏移问题大致可以分为以下三步：

(1)求导，获得函数的单调性，极值情况，作出图像，由题意得知x1,x2的范围(数学结合思想);

(2)构造函数:

①x1+x2>(<)2x0型的结论构造函数f(x)-f(2x0-x)；

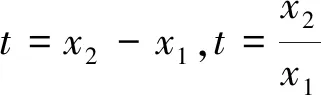
③替换函数法构造函数；

④对数平均不等式构造函数;

(3)求导，限定范围，判断符号，获得不等式，证明得出结论.