利用“同解方程”简化解析几何的运算
江苏省海安市实验中学 (226600) 潘新峰
解析几何是指借助笛卡尔坐标系,利用方程来研究几何对象之间的关系和性质的一门几何学分支.高中阶段所学曲线都是用方程来表示的,曲线上所有的点的坐标都是方程的解,以方程的解为坐标的点都在曲线上,即曲线的方程、方程的曲线.本文重点关注利用“同解方程”以减少解析几何的运算量.
一、同解原理
原理:已知二次函数f(x)=a1x2+b1x+c1、g(x)=a2x2+b2x+c2,若f(x1)=f(x2)=0且g(x1)=g(x2)=0,其中x1≠x2,则存在λ∈R且λ≠0,使得a1=λa2、b1=λb2、c1=λc2.
证明:因为g(x)=a2x2+b2x+c2,若f(x1)=f(x2)=0且g(x1)=g(x2)=0,所以根据因式分解的理论一定有,f(x)=a1(x-x1)(x-x2)且g(x)=a2(x-x1)(x-x2),于是存在λ∈R且λ≠0,使得f(x)=λg(x),即存在λ≠0,使得a1=λa2,又b1=-a1(x1+x2)且b2=-a2(x1+x2),所以存在λ≠0,使得b1=λb2,同理存在λ≠0,使得c1=λc2.
二、例题选讲
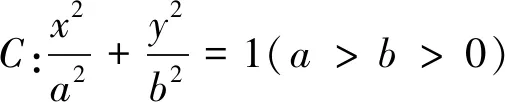

图1
(1)求椭圆C的方程;
(2)设经过点P(2,0)的直线l交椭圆C于A,B两点,点Q(m,0).
①若对于任意直线l总存在点Q,使得QA=QB,求实数m的取值范围;
②设点F为椭圆C的左焦点,若点Q为ΔFAB的外心,求实数m的值.
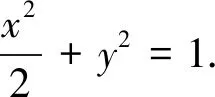
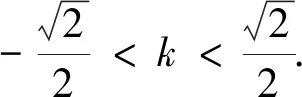


例2 (2008年江苏高考18题)设平面直角坐标系xOy中,设二次函数f(x)=x2+2x+b(x∈R)的图像与两坐标轴有三个交点,经过这三个交点的圆记为C.
(1)求实数b的取值范围;
(2)求圆C的方程;
(3)问圆C是否经过某定点(其坐标与b无关)?请证明你的结论.
解析:(1)易得实数b的取值范围为(-∞,0)∪(0,1).

方法二:设圆C的方程为x2+y2+Dx+Ey+F=0,令y=0得x2+Dx+F=0,由于抛物线和所求圆都通过x轴上相同的两点,所以方程x2+Dx+F=0与方程x2+2x+b=0必然同解,于是解得D=2、F=b,在把点(0,b)代入圆的方程,解得E=-(b+1),故所求圆C的方程为x2+y2+2x-(b+1)y+b=0.
(3)易得圆C过定点(-2,1)、(0,1).
评注:通过例1的解析和例2中两种方法的比较,我们可以看出,利用同解原理求曲线方程中的参数.可以大大的减少运算量.
三、巩固练习

(1)求椭圆的标准方程;
(2)直线y=x+1和椭圆交于A,B两点,求过三点A,B,F的圆的方程.



图2
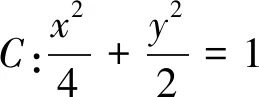
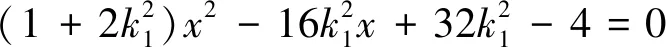
评注:考虑到A、B关于x轴对称,它们的横坐标相等,又点A、B、E均在椭圆上,故可以利用“同解方程”的方法来解决这个问题.
四、结束语
近年来解析几何解答题往往是高考中区分中上层学生数学成绩的一个关键考点.解决此类问题时的理念是数形结合,方法有“线切入”和“点切入”(见例题1).其中对能力的要求主要体现在如何选择变量和合理的运算路径上,从而解析几何的主要特征是“算”.考生如果对运算方法运用不当,面临繁杂的运算将无从下手,最终只能望运算而兴叹,以失败告终.我们要引导学生根据题目的特征选择合理的方法,尽可能地简化运算,在解决解析几何问题时就会做到胸有成竹,举重若轻,这正是笔者写这篇文章的用意所在.

