一道高二数学期考题的解法探究
2020-05-13 13:51:34陕西省汉中市四五学校723312侯有岐
中学数学研究(江西) 2020年3期
陕西省汉中市四〇五学校 (723312) 侯有岐
在近年的各类考试中,经常涉及三角形面积及相关问题的最值或取值范围的问题.此类问题往往前景活泼多样,难度较大,解决的思维方式多变,解决的方法也多种多样.因此一直备受命题者的青睐.这里以一道高二考试题为例,探索如何解决此类问题的常见解法,希望有益于大家理解题目的本质,同时注意体会在解题过程中,如何适时实施转化化归的方法.
一、试题呈现
题目(2019年洛阳市高二数学考试第12题)

本题通过已知三角形中有关边长及点的特殊位置,进而求解三角形面积的最大值.解决问题时可以从“数”的角度和“形”的角度两方面入手,使数与形有机结合,这样就可以利用多种思想方法完成,从而有助于学生数学学科素养的培养.
二、多解思维

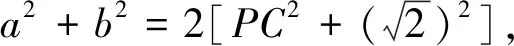
设ab=t(ab≥2),则y=-3t2+24t-36
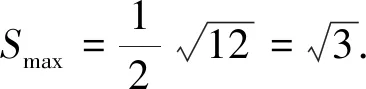


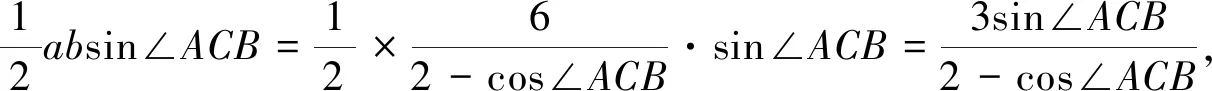
思维角度3:根据已知及“点P是AB的中点”,由三角形中线定理得到a,b的关系式a2+b2=4ab-4,由余弦定理得8=a2+b2-2abcos∠ACB,两式结合得出6=ab(2-cos∠ACB),再利用系数的转化与配对并结合不等式(a2-b2)(c2-d2)≤(ac-bd)2(当且仅当bc=ad时取等号)*得出三角形面积的最大值.
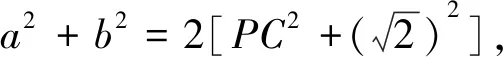
三、解后反思
三角形问题是高考中常考的考点.解决此类问题时,不但要时刻想到正、余弦定理,而且要熟悉三角形的性质和三角函数、向量等有关知识.这类题目一般要求学生会运用数形结合和转化化归等数学思想方法从几何角度来寻找解题途径,然后通过适当的代数运算加以解决,所以在平时的教学活动中,要指导学生细心审题,认真计算,合理转化,逐步培养学生思维的创新性,提高学生的数学解题能力.
猜你喜欢
中学生数理化·高二版(2024年2期)2024-06-17 17:49:31
中学生数理化·高二版(2024年2期)2024-06-17 17:49:31
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
文理导航·科普童话(2017年7期)2018-02-10 19:42:29
小天使·四年级语数英综合(2017年6期)2017-06-07 10:45:55
智富时代(2017年4期)2017-04-27 02:13:48
新高考(英语进阶)(2017年2期)2017-04-16 05:24:01
小天使·二年级语数英综合(2017年3期)2017-04-01 20:49:17

