坐标系与参数方程几种常见题型的解法
安徽省枞阳县会宫中学 (246740) 方明生
坐标系与参数方程作为高考的选考内容之一,笔者在高考阅卷中发现,相对于绝对值不等式而言,大部分学生都会选择坐标系与参数方程的这一题.尽管学生在平时的学习中进行了多次的模拟考试以及大量训练,但在实际解题过程中依旧会出现障碍.第一问一般考察基本知识,主要涉及参数方程、普通方程和极坐标方程三者间的相互转化,此问5分学生基本都能够得到.相对于第一问而言,第二问的得分却大打折扣,究其原因,主要是学生在解题的过程中没有完全明白命题老师的意图,解题的方法不当导致运算量增大或者无从下手,笔者根据近几年的高考试题,对于第二小问常考题型进行了整理,供各位方家指正.
一、利用直线参数方程t的几何意义

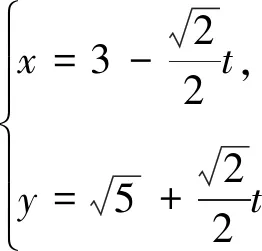

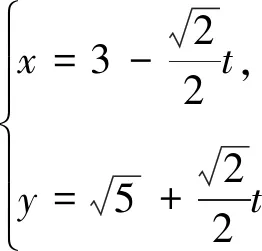

评注:利用极坐标公式ρ2=x2+y2,x=ρcosθ,y=ρsinθ进行化简即可求出圆c普通方程,再将直线的参数方程代入圆C的直角坐标方程,得到关于参数t的一元二次方程,结合参数t的几何意义利用根与系数的关系即可求得|PA|+|PB|的值.
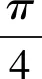
(-2,-4)的点P,且直线l与曲线C相交于A,B两点.
(1)写出曲线C的直角坐标方程和直线l的参数方程;

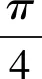

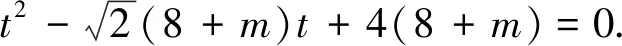
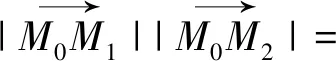
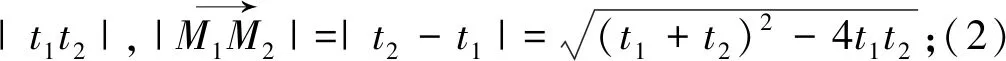
二、利用极坐标ρ的几何意义
例3 (2017全国Ⅱ)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
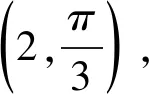
解析:(1)设P的极坐标为(ρ,θ)(ρ>0),M的极坐标为(ρ1,θ)(ρ1>0)由题设知|OP|=ρ,
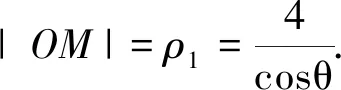
(2)设点B的极坐标为(ρB,α)(ρB>0).由题设知|OA|=2,ρB=4cosα,于是ΔABO面积S=
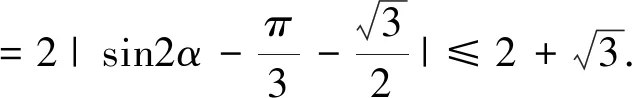
例4 (2016全国Ⅱ)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;

解析:(1)由x=ρcosθ,y=ρsinθ可得C的极坐标方程ρ2+12ρcosθ+11=0.
(2)在(1)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).
由A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程得ρ2+12ρcosα+11=0.由韦达定理可得ρ1+ρ2=-12cosα,ρ1ρ2=11.

评注:此处所选取的两个例题均为高考原题,如果大家认真去研究的话会发现它们有共同之处是所给直线为经过原点(即直线的极坐标方程θ=α(ρ∈R))的特殊直线,利用极坐标的几何意义求解.
三、利用普通方程联立求解
例5 在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ-3=0.
(1)求C2的直角坐标方程;
(2)若C1与C2有且仅有三个公共点,求C1的方程.
解析:(1)由x=ρcosθ,y=ρsinθ可得C2的直角坐标方程为(x+1)2+y2=4.



评注:本题明显不符合前面的两个题型,对于此类问题,我们都可以用通性通法去解决,借助普通方程进行考查的是有关坐标系与参数方程的问题,涉及到的知识点有曲线的极坐标方程向平面直角坐标方程的转化以及有关曲线相交交点个数的问题,在解题的过程中,需要明确极坐标和平面直角坐标之间的转换关系,以及曲线相交交点个数结合图形,将其转化为直线与圆的位置关系所对应的需要满足的条件,从而求得结果.
通过上述三种题型的解答,可以解决坐标系与参数方程问题可以归纳为:“参”代“普”、“极”代“极”、“普”代“普”三种题型,审题的时候要搞清楚出题者的意图,要学会抓住题干,如果直线是标准参数方程,对涉及过定点M(x0,y0)的线段问题,优先考虑采用“参”代“普”法,直线过原(极)点,涉及到求线段长时,优先考虑用极坐标求解,对于以上两种方法行不通的时候就可以采用“普”代“普”.在平时的学习中,应该多加归纳,灵活应用,方可优解.

