基于一道高考题的多解探究及思考*

广西师范大学数学与统计学院 (541006) 刘存华 周 莹广西民族大学理学院 (530006) 毋晓迪

波利亚曾说：“中学数学教学的首要任务就是加强解题”.解题并不意味着题海战术，反而是要以经典题型为载体，通过“一题多解”来串联知识模块，培养思想方法，激发学生学习欲望[1]，真正实现“鱼渔欲”一体解题教学.下面以2019年高考全国III卷的一道平面几何题为例，探究八种不同维度和层次的解法，与一线教育者共同交流一题多解教学.

1.呈现试题

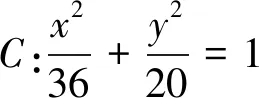
评析:本题从椭圆出发设题，同时夹杂着象限、三角形、坐标等多个知识点，完美地将“直线与方程”、“圆与方程”、“圆锥曲线与方程”、“三角函数”、“平面向量”等多个知识模块串联起来考察.因此，意味着本题有多个角度和方向的解法.

2.试题解法探究

2.1 余弦定理法

拟定计划：本题目标是求出点M的坐标，所以直接设该点为M(x0,y0).根据题干条件，运用椭圆的定义易求得|F1F2|=|F1M|=8、|F2M|=4.观察ΔMF1F2和RtΔMDF1可知∠MF1F2为公共角，将其作为中介量，先在ΔMF1F2中运用余弦定理求出该角的余弦值，随后在RtΔMDF1中可求出F1D的长度，也就得出了M的坐标.

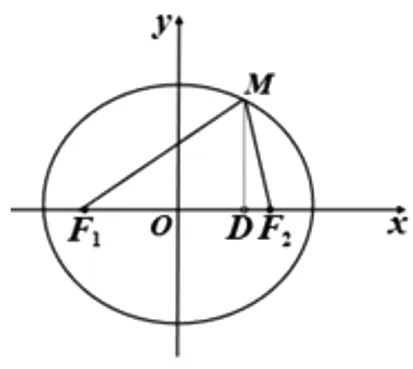
图1

解析：由题意|F1F2|=|F1M|=8，由椭圆定义得|F2M|=12-8=4.如图1，过点M做x轴的垂线，垂足为点D,设点M(x0,y0)，在ΔMF1F2中，由余弦定理得cos∠MF1F2

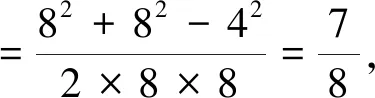
2.2 勾股定理法

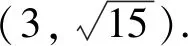
评注：仍然从未知量出发，假设点M的坐标为(x0,y0)，再观察图形可知MD为RtΔMDF1和RtΔMDF2的公共边，所以就以MD为中介量，在两三角形中，用不同的量来表示MD，即可求出点的坐标.

2.3 等腰三角形的性质法

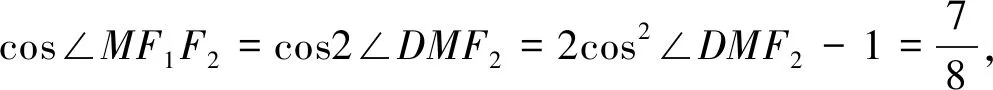
评注：从未知量出发，欲求点M坐标，先求纵坐标.观察在ΔMDF2中，若知道cos∠DMF2，即可求得MD.那么如何求cos∠DMF2？利用“ΔMF1F2为等腰三角形”即可.

2.4 椭圆与圆的位置关系法

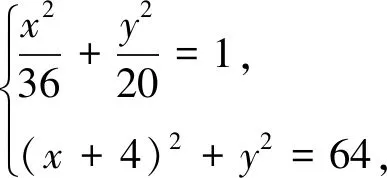
评注：从题干条件“ΔMF1F2为等腰三角形”出发，|F1M|=|F1F2|，因此可以将M点视为以点F1为圆心且F1M为半径的圆与椭圆的交点，联立圆和椭圆的方程可求出在第象限的交点，即M点坐标.

2.5 参数法

解析：由于点M在第一象限，可设M(6cosθ,

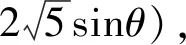
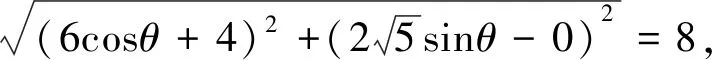
评注：从题干条件“ΔMF1F2为等腰三角形”出发，|F1M|=|F1F2|=8，又因为点M在椭圆上，因此可联想到用参数法将其表示出来，然后根究两点距离公式即可求出坐标.

2.6 焦半径公式法

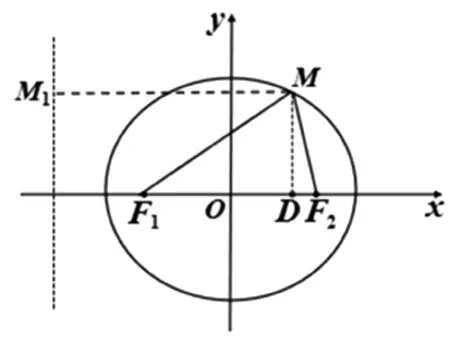
图2

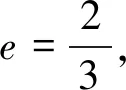
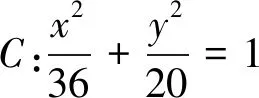
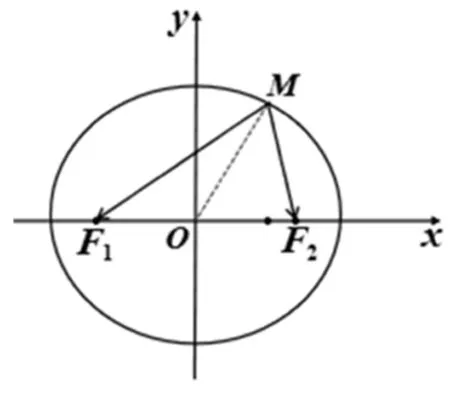
图3

2.7 中线长公式法

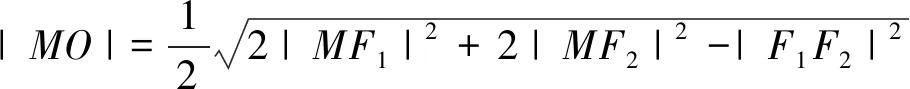
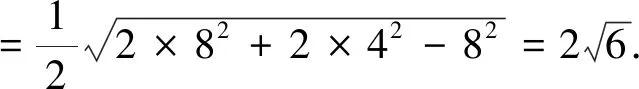
评析：从椭圆性质出发观察图形，可知在ΔMF1F2中，OM为其中线，因此可以依据中线定理求得MO的长度.然后，将点M视为以O为圆心且MO为半径的圆与椭圆的交点，因此可以联立方程即可求解.

2.8 等面积法+极化恒等式法

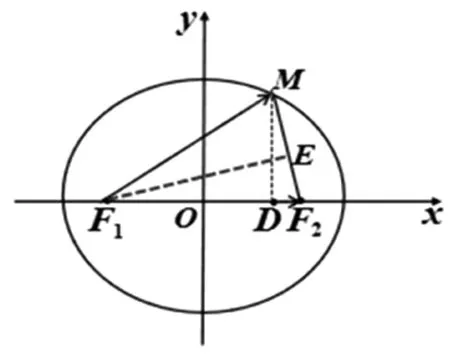
图4

解析：如图4，过点F1作FE垂直于MF2于E，过点过M做MD垂直于F1F2，又

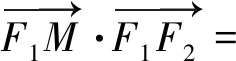
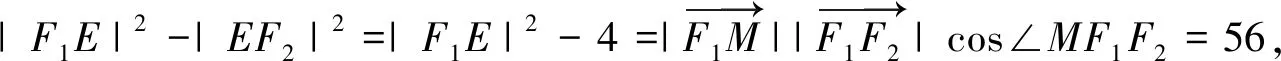
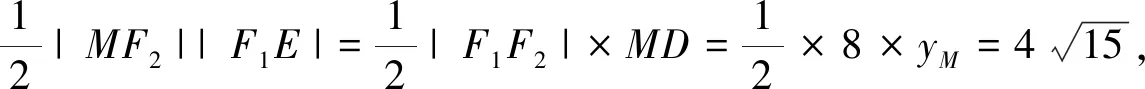
评析：从结论入手，欲求点M的坐标，可先求其纵坐标，即求MD.利用极化恒等式可以求得F1D，可以联想到三角形等面积法，通过不同的底边和高以面积为中介量，从而推算出MD.

3.回顾反思

3.1 一题多解的“套路”

一题多解的根本原因是从不同的侧面去观察题目，从不同的维度去思考和使用条件[2].总结上述的八种解法，可得知一题多解的常见思考方向：(1)从未知量出发，反向逆推，对条件进行不同的转换和运用，例如解法1-3；(2)从题干主要条件出发，联想相关知识点，顺势推出结果，例如解法4-6；(3)从图形特征出发，观察点、角、线、图形，根据特殊性构造思路，例如解法7；(4)运用不同的思想方法进行整体思考，例如解法8.

3.2 一题多解的“技巧”

思维并不是单向的，常常运用多个角度同时思考得出结果.例如，解法1同时运用了三个方向，从结果出发，根据题干椭圆定义、等腰性质，并观察图形得知公共角，从而运用余弦定理求解.因此多种不同的解法可以发散学生的思维，培养思维能力.

3.3 一题多解的“功效”

各种解法各有特色：解法1-2较为符合学生的原有解题思维，易于接受；解法3复习了等腰三角形的性质；解法4训练学生从图形之间的关系思考问题；解法5运用参数法，复习两点距离公式，计算简便；解法6复习椭圆离心率的计算公式；解法7复习中线长公式，在联立方程；解法8培养学生的等面积法，而且拓展了“极化恒等式”，解法独树一帜.一题多解可以运用不同的解法激发学生的兴趣，同时还串联各个板块的知识点，回顾常见的思想方法.

一题多解可以用一道经典题，帮助学生复习多个知识(鱼)，讲授不一样的思想方法(渔)，激发学生的学习情感(欲)，达到“鱼渔欲”的三位一体教学功能[3]，进而提高学生学习效率.