HHT的改进及其在电压闪变分析中的应用

孙松源

（1.中国电子科技集团公司第四十一研究所，安徽 蚌埠 233000；2.电子信息测试技术安徽省重点实验室，安徽 蚌埠 233000）

一、引言

电压闪变作为评定电能质量的重要指标，能够直接、迅速反映出供电质量。常用的电压闪变分析方法有半波有效值法、平方解调法、全波解调法等，但这些方法均不适用于时变的电压闪变信号的时频分析。希尔伯特-黄变换（Hilbert-Huang transform）是一种自适应的非平稳、非线性信号处理方法[1]。在许多非线性、非平稳信号处理的研究领域得到了很好的应用。

希尔伯特-黄变换方法的主要由EMD分解和离散Hilbert变换组成，通过EMD分解将电压波动信号分解成固有模态函数分量（Intrinsic Mode Function，IMF），再对IMF进行离散Hilbert变换求解各个分量的瞬时频率和瞬时幅值。但是在EMD分解过程中主要存在三个方面的问题：端点抖动问题，停止准则的选择问题，虚假IMF分量的去除问题。

二、端点抖动

EMD分解方法首先对电压波动信号提取上下包络线，在提取上下包络线的过程中需要提取局部极大值和局部极小值，而极大值和极小值一般不会落在电压波动信号的首尾，所以在对极大值拟合插值提取的上包络线和对极小值拟合插值提取的下包络线一般不包含边界端点。由于插值计算需要包含边界端点，在对边界端点进行插值处理时，会出现严重的失真情况。另外EMD分解方法产生的每一个IMF分量是建立在前一个IMF分量的基础上，失真情况会传递到所有IMF分量，对所有分解的IMF分量结果造成影响，误差会传递到后续的计算过程中，造成计算结果误差偏大。

目前，解决端点效应的方法主要有特征波法[2]、ARMA模型对时间序列进行外延[3]、SVM数据延拓[4]、线性外延方法、端点镜像法[5]。其中端点镜像法在准周期信号和随机噪声信号分析方面准确性较高。

本文采用极值点为对称点对信号进行延拓，在首端延拓一个极大值和一个极小值，在尾端也延拓一个极大值和极小值，即：

首端：Tmax延拓=2*T[1]-Tmin[1]，Ymax延拓=Ymax[1]

Tmin延拓=2*T[1]-Tmax[1]，Ymin延拓=Ymin[1]

尾端：Tmax延拓2=2*T[cnt]-Tmin[N]，Ymax延拓2=Ymax[M]

Tmin延拓2=2*T[cnt]-Tmax[M]，Ymin延拓2=Ymin[N]

其中：cnt为采样数据点数，N为提取的局部极小值点数，M为提取的局部极大值点数。

采用该方法延拓前后的IMF分解结果分别如图1和图2所示。

图1 未采用延拓所提取的包络线示意图

图2 延拓之后提取的包络线示意图

由图2可以看出采用本文的延拓方法处理后的包络线很好的消除了端点抖动的问题，并且在边界点处的拟合插值符合数据趋势。

三、停止准则

EMD分解IMF分量过程中，由于提取过程中上下包络线不是完全对称的，其均值不为0，因此设置一个计算的逼近值来确保分解能够结束，不会过分解，该值取值范围一般为0.2-0.3[6]。为了得到局部均值为零的IMF，最初提出的计算停止准则是：

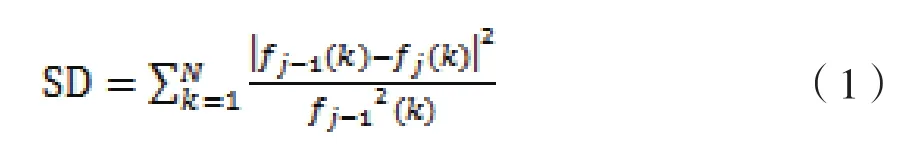
其中：fj-1为前一次分解的结果

fj为当前次分解的结果

由上式可以看出，前一次分解结果中的零值会对计算值产生比较大的影响，为了消除该影响，将上式变换为如下形式：

通过实验，式2的收敛速度和分解效果比式1要好。

四、虚假分量

实际在对电压波动信号进行EMD分解时，由于包络线的均值不为零，需要通过设置的停止准则值来结束分解。由于信号本身含有噪声，以及在计算过程中的误差，实际分解会产生一些无关的低频IMF分量。本文采用相关系数法去除虚假的IMF分量。

利用相关系数法去除电压波动信号的IMF虚假分量是将电压波动的IMF分量与提取的电压波动做相关系数计算，如果IMF分量与电压波动的相关系数较大，则认为是有效的IMF分量；如果相关系数较小，则认为是虚假IMF分量。

采用的方法是：

首先，计算各个IMF分量与电压波动的相关系数值，计算公式如下所示：

其中：pi为第i个IMF分量与电压波动的相关系数值

fi(n)是第i个IMF分量

v(n)是电压波动值

N是采样点数

其次，设定阈值，阈值的设定公式如下所示：

其中：pi为第i个IMF分量与电压波动的相关系数值

k为EMD分解的IMF分量个数

最后，根据阈值和相关系数值剔除虚假分量。

本文采用以下试验信号对相关系数法去除虚假分量进行了试验验证：

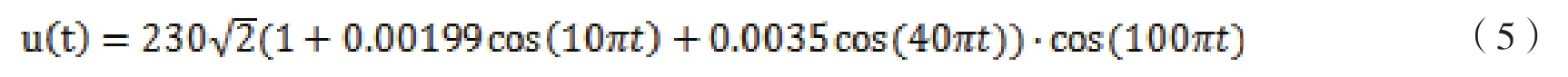
其瞬时频率和瞬时幅值计算结果分别如图3和图4所示。

图3 瞬时频率示意图

图4 瞬时幅值示意图

对比信号表达式可知IMF分量3和分量4是虚假分量。

使用相关系数法，计算得到4个IMF分量的相关系数值依次分别为：0.8384859977251149、0.533131290239601、0.00022524614810904791、0.0012572281439647524。按照本文方法对应的阈值设为0.209621499431278725，以此便可以去除掉IMF分量3和分量4。

由试验结果可以看出本方法可以很好的去除掉IMF的虚假分量。

五、电压闪变的计算分析

在准确地获取了IMF分量后，即可计算各个IMF分量的瞬时频率对应的单位视感度的波动值，由瞬时幅值和瞬时频率对应的单位视感度波动值计算瞬时视感度值s(t)，再按照下式计算得到短时闪变的严重度[7]：

其中：P0.1、P1、P3、P10、P50为统计的 s(t)超过0.1%、1%、3%、10%、50%的时间比。

六、结语

本文分析了希尔伯特-黄变换在分析电压闪变过程中的存在的问题，并有针对性地进行了改进，同时对改进方法进行了试验验证，由试验结果可看出改进后的希尔伯特-黄变换能够更准确的计算分析电压闪值。