巧用学生错误资源 助力教师顺错思措
曹艳红
摘 要:核心素养日益成为引领课程改革、教学变革、教学评价等教育活动的第一推动力。作为一线教师,如何正确处理学生数学学习经验中的“错误”,关系到每一位学生数学核心素养的养成。受学习负迁移的干扰、日常生活中的错误经验误导以及自身缺乏逆向思维等因素的影响,学生在学习过程中常常错出有因,教师可以通过创设安全、自由的课堂氛围,让错误浮出水面,善用学生错误资源,进而打造灵动课堂,激发课堂活力。
关键词:小学生;核心素养;错误资源;顺错思措
中图分类号:G62 文献标识码:A 文章编号:1673-9132(2020)14-0147-02
DOI:10.16657/j.cnki.issn1673-9132.2020.14.072
近年来,“核心素养”日益成为全球范围内教育理论与实践研究的热议话题。“核心素养”逐渐成为课程改革、教学变革和教学评价等教育活动的第一推动力。21世纪初,以美国为代表的国家和地区开始着手于以“素养”为核心的课程改革。2014年,教育部《关于全面深化课程改革,落实立德树人根本任务的意见》的颁布,意味着我国的教育改革从“知识核心”时代开始走向“核心素养”时代。核心素养的养成是奠定每一位儿童学力发展的基础,更是培养儿童终身学习能力的基石。
2011版的《义务教育数学课程标准》中并未对“数学核心素养”作出具体化定义,但提出了包含数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识十大数学核心概念。一言以蔽之,核心素养是包括知识、能力、态度等在内的综合素养。新课标提出“变教为学”的基点就是对学生经验的充分尊重和利用。作为一线教师,如何正确处理学生数学学习经验中的错误,关系到每一位学生数学核心素养的养成。
一、学生:“错”出有因
受年龄、身心发展和认知能力等因素的影响,学生在学习过程中会产生各种各样的错误。寻迹追因,从心理学视角来看,易受学习负迁移的干扰;从已有经验来看,常常受日常生活中错误概念的误导;从思维发展来看,跟学生逆向思维的欠缺无不相关。
(一)学习负迁移的干扰
心理学指出:负迁移是指前面学习的知识对后面学习产生的消极影响或干扰作用。换言之,学生学习了前面的知识后,容易出现思维定式,这时就可能产生学习负迁移现象。
算术思维的负迁移给学生的学习造成了一定的困扰。在学习用方程解决实际问题时,很多学生仍对算术方法“情有独钟”,对方程法却是“朝三暮四”。例如,列方程解决实际问题:“已知一个梯形的面积是22平方厘米,高是4厘米,上底是5厘米,下底是多少厘米?”一位学生列出方程:x=22×2÷4-6。
这位学生的解题形式上看似是方程,实质上还是算术思维主导。针对这类问题,教师要多关注学生代数思维的发展与数学表达。教师对学生的算术法表示认可的同时,追问:“能不能从题目中的数量关系出发,找到未知量与已知量之间的等量关系式?”循循善诱,引导学生建立代数思维,培养学生的抽象逻辑思维。
(二)生活中错误经验的误导
在日常生活与学习的过程中,学生积累了大量的经验,其中一些符合现代科学的理解,而有些则与科学的理解相悖。研究学生生活中的错误性经验,是一线教师系统化探究学生认知世界的开始。
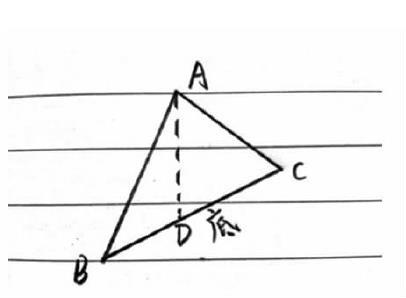
例如,由于受到日常概念的影响,学生对“垂直”的意向是以地平面为参考系。当要求作出下图三角形ABC的BC边上的高时,常有学生错误的作出了AD这条线段作为三角形BC边上的高。
學生在生活中接触的“高”具有唯一性,即以水平方向为底,高的方向往往都是垂直的。然而,数学中三角形的“高”却复杂多样,由于三角形有三条边,相对应的“高”就会随着底的变换而变化。如上图所示,当以斜边BC为底时,所对应的高便不再是垂直方向,这与学生的生活经验相违背,学生理解较为困难。因此,教学过程中教师要重视这类典型案例,实施有效的教学手段,辨析三角形的高与生活中的高的区别与联系。利用变式,变换三角形的位置,促进学生理解数学中的“高”,进一步明确三角形底与高的相互对应关系。
错误概念的形成不能仅仅归因于理解偏差或遗忘因素,它往往与日常经验联系密切。若教学只关注新知识的授受,而正确概念的传授并不能自动纠正学生原有的错误观念。所以,教师必须寻求转变学生错误概念的方法和策略。
(三)逆向思维的欠缺
很多学生出现错误,尤其是计算类的错误,原因多种多样,但最主要还是跟学生自身不具备逆向思维有关。大部分学生在检查题目时,只会按原来的解题思路进行复核,那么答题的准确性与速度就大打折扣。
学生在求形如a-bx=c方程的解时,错误率通常很高。除了对于等式的性质理解不透彻之外,也与学生逆向思维的欠缺密切相关。例如,方程56-x=15,从56中减去一个数,差为15,那么这个数不可能比56还要大。如果学生能够将得到的未知数的值代入方程检验,而不是简单地计算15+56的值是否正确,那么学生能够发现错误的可能性将大大提高。
例如,“大、小两桶油共重36千克,如果从大桶中倒4千克油到小桶中,那两桶油就正好一样重。原来大桶油和小桶油分别重多少千克?”很多学生往往误以为大桶中油比小桶多4千克。倘若学生能够逆向思考——如果大桶的油只比小桶的油多4千克,当从大桶中倒了4千克油到小桶中,大桶油和小桶油的质量不可能一样重。那么,学生就更有可能推翻自己错误的思维方式。
逆向思维是重要的数学思维方式之一。正向思维与逆向思维的交替灵活应用是学生思维成熟的重要指标。事实上,在课堂教学中,许多教师常常只关注正向思维的训练,反向验算流于形式。长此以往,学生的正向思维定式往往会造成解题思路的刻板与僵化。学生出现的错误是思维深入的有效载体。因此,进入学生错误深处,可知很多学生的逆向思维得不到训练,进而引发类似错误的发生。
二、教师:顺“错”思“措”
英国心理学家贝恩布里奇曾提出:“错误人人皆有之,作为教师不利用是不可原谅的。”面对学生有价值的错误,作为一线教师,需要课前积极寻找错误资源、精心预设,在安全、自由的课堂氛围中及时捕捉、利用错误资源,课后及时反思错误,将错就“措”,将数学错误资源化。
(一)课前积极寻找,精心预设——显错与隐错同在
出错是学生的权利,我们要宽待学生的错误,将宝贵的错误可视化、资源化。错误可能有无穷的结合方式,可谓复杂多样。就其隐匿程度来看,可以分为显见性错误和隐匿性错误。
对学生显见性错误,具有丰富教学经验的教师往往关注较多。显见性错误往往都是学习目标中的重难点。这些错误是已知的,是课前可以预设的。因此,教师课前在进行教学设计时,需深入研究学生可能出现的各种错误以及应对方式。
而隐匿性错误往往因隐藏极深而极易被忽略。教师课前精心预设显见性错误的同时,更要关注隐藏极深之下的谬误。如何挖掘学生隐匿性错误,除了和教师的教学经验有关,更与教师自身扎实的专业素养密切相关,尤其是对于教学内容本质的理解与掌握,学生认知水平和可能的判断。教师多阅读数学史、数学思想史等专业书籍,对了解数学知识,深入数学内部,展现数学自身魅力大有裨益。
(二)课上创设安全、自由的氛围——拾错与引错并进
“新课标”指出:真实的数学教学过程是师生交往互动、共同发展的过程。虽然教师课前做了精心预设,但真实的课堂上往往会发生“可遇不可求”的意外,不可避免地出现意外错误。错是学生认知不畅时出现的状况,值得我们重视和尊重,应该很好地掘之、用之。
在安全、自由的课堂中,教师的理解和宽容、鼓励与帮助,能促进学生理清思维,提升认识。这就需要我们教师充分发挥教育机智,在真实的教学课堂中,及时捕捉学生有价值的错误,主动“拾”错,因势利导,积极“引”错,化弊为利,展开充分讨论,促进学生知识的建构。教师可以在课堂讨论中,多询问一句:“还有不同的想法吗?”少一些理所当然地、武断性地否定性话语,给学生留下思考空间,从而使学生获得更丰富的体验和学习经验。
(三)课后及时反思,将错就“措”——究错与悟错共存
教学过程中学生错误的呈现,正是暴露了学生的已有认知水平以及认知结构中的模糊区或盲区。教师课后及时反思、研究这些错误资源,为下一次教学提供有利素材。同时,小错误也有可能引发大思考。尤其是学生看似马虎、粗心所导致的错误背后往往跟教師的教学方法、评价方式等方面密切相关。
例如,成绩优异的学生却出现口算错误现象,这类学生往往求胜心过强,过分追求速度。这就暴露出我们的评价方式出现了偏离,即过分强调速度,而忽略了准确性这一先决条件。因此,教师可以适当调整评价方法,让“首先是正确,其次才是有一定的速度,最后再追求算法合理,灵活”的要求落到实处。
因此,正确看待每位学生的错误,是对每一个生命体的尊重。不妨将学生的错误作为一种宝贵的教育资源,以促进学生智力提升和情感发展。学生在错误中丰富体验、积累经验,教师也能在错误中不断提升自身专业素养。
在日益标准化的评价体系下,教师对待学生的“错误”嗤之以鼻,学生对待自己的“错误”唯恐不及。久而久之,在过分追求理性思考的境遇下,年级越高,学生敢于冒险的可能性就越小。
21世纪是一个追求创新力的社会,需要创造力强和想象力丰富的人才。课堂教学不仅要激发学生的求知欲,还要给予学生犯错误的机会和勇气。因此,教师在教学过程中,要敢于面对学生的错误,善用学生错误,“错误之花”才能绽放长存。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]华应龙等.小学数学化错教学案例[M].北京:中国人民大学出版社,2018.
[责任编辑 谷会巧]

