高中数学教学要做到:于含糊处不含糊
黄鹏程

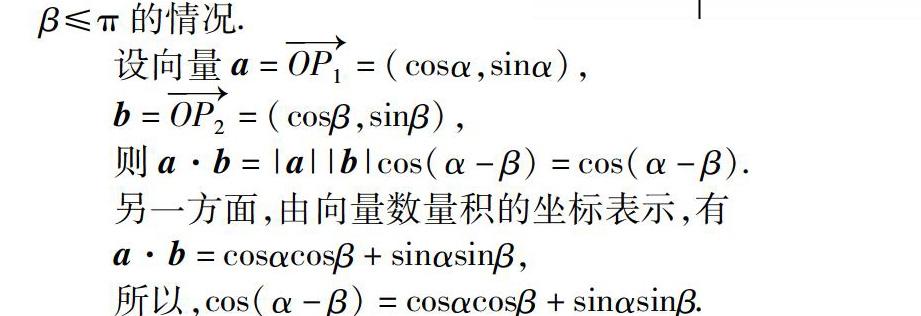

【摘要】高中数学教师要进行“深度教学”,准确把握学情和深刻解读教材至关重要,因为它们是引导“深度学习”的基点.因此,实现“深度教学”首当其冲的一条就是数学教师要进行“深度学习”.近期,笔者作为评委参加了市高中数学青年教师优秀课比赛活动,感触颇深,现将自己的一些体会与想法记录下来,希望与数学同仁做进一步的交流和探讨.
【关键词】高中数学;“深度学习”;体会与想法
【基金项目】本文系江苏省扬州市教育科学“十三五”规划立项课题“关于微探究应用于高中数学教学的研究”成果,课题编号:G/16/P/035.
高中数学青年教师优秀课比赛的课题是“两角和与差的余弦”,这一节课是三角函数概念和诱导公式等知识的延伸,是两角和与差的正弦、正切以及二倍角公式等知识的基础.对三角变换、三角恒等式的证明和三角函数式的化简、求值等问题的解决有重要的支撑作用.它的重点和难点在于公式的运用与证明.我们先来看看教材中的处理:
在直角坐标系xOy中,以x轴为始边分别作角α,β,其终边分别与单位圆交于P1(cosα,sinα),P2(cosβ,sinβ),则∠P1OP2=α-β.由于余弦函数是周期为2π的偶函数,所以,我们只需考虑0≤α≤β≤π的情况.
教材中利用向量這一工具,采用将数量积“算两次”的办法推导两角差的余弦公式.应该说这种证明手法非常灵巧,将向量的工具性作用发挥得淋漓尽致.可问题在于,当我们将引例中特定的角推广到一般的任意角时,α-β还是不是向量 OP1=(cosα,sinα)与向量OP2=(cosβ,sinβ)的夹角呢?教材之中仅以一句“由于余弦函数是周期为2π的偶函数,所以,我们只需考虑0≤α≤β≤π的情况”轻轻带过,可谓在关键之处“含糊”了.事实上,比赛中有两位老师就是按教材中的这种处理照本宣科,当然面对课堂中学生明显呈现出的迷惑,老师根本不敢在这里纠缠,显然是对这段文字的背后缺少深入的思考,因而也就没有了主动驾驭课堂的底气.因此,这就反映了老师们没有完全精准地把握住问题的根源.造成理解上出现“含糊”的问题是学生对“两种角”的认知产生了冲突.实际上,两个向量的夹角是由表示向量的两条有向线段共起点所形成的平面角,它的范围是[0,π],是一种只论张合程度的“几何角”,而角α-β是放置在坐标系内的角α,β(以x轴为始边旋转)的“差角”,其范围是(-∞,+∞),是一种大小与旋转的方向和旋转的圈数有关的“代数角”.
在这里,如果我们引导学生进行“微探究”,探究问题为:如何将这个“几何角”向“代数角”转化?最终可发现,事实上只需分两种情况即可:
① 当点P1在直线OP2上或上方时,角β+θ与角α终边相同,故α=β+θ+2kπ,k∈Z,即α-β=θ+2kπ,k∈Z;
② 当点P1在直线OP2下方时,角β-θ与角α终边相同,故α=β-θ+2kπ,k∈Z,即α-β=-θ+2kπ,k∈Z.
接下来的证明已经顺理成章了.
然而引起笔者更多思考的是,从中反映出当前高中数学教学的功利化现象令人堪忧,充分研磨的赛课对课本中的“模糊”之处的处理尚显不足.推想一下,日常教学中淡化概念原理公式的生成,而急于切入数学应用,恐怕已成为当下高中数学教学的常态.长此以往,学生无法形成或者无法完全形成数学学科的核心素养.
需要指明的是,我们今天谈核心素养不是喊口号,不是玩文字游戏,更不意味着对过去的全盘否定.其实,课堂只要存在,课堂教学改革就永远不会停下前进的步伐.不难发现,数学教学的改革总是伴随着课改理念的革新而不断推进的,而数学教学的实践又促使课改理念的永不停步地革故鼎新,并且每一次新理念的提出都是对过去观念的批判性继承,并进行不断地丰富和发展,使教育教学目标的实施一步步变得更加具体、明确、可操作.
从本文所讲的教学案例看来,要想把培养学生数学学科核心素养的工作真正落地生根,基于核心素养形成的“深度学习”课堂——“深度教学”理所当然成为当前教育形势下的必然之选.因为“深度学习”是内源性学习,只有“深度学习”才可能发展学生的数学素养.我们这里所讲的“深度学习”不是机械学习研究领域的概念,它是指运用所学的本学科知识和跨学科知识,运用常规思维和非常规思维,将所学的知识和技能用于解决实际问题,以发展批判性思维、创新能力、合作精神和交往技能的认知策略,与传统的外部灌输、被动接受的“浅层学习”相比具有强化情感驱动、立足问题解决、强调课程整合、突出思维深度等特征.从本文所论及的案例可见,要想使学生在课堂中能够进行“深度学习”,在课堂教学中引入“微探究”,是一个不错的解决办法.
总之,在数学教学中,教师要对数学文本尤其是数学教科书进行深入地学习和研究,通过数学文本的精读细研,决不放过每一个“含糊之处”,发现并理解其数学本质.只有当教师真正“吃透”所要教授的内容,才能深入浅出地、有针对性地设计教学内容,才能充分关注课堂中学生的深度参与和深度思维组织课堂教学,不仅要教会学生解题,更要让学生了解知识的来龙去脉,掌握学习方法,学会与人合作,培养创新能力和理性精神.
【参考文献】
[1]孙宏安.数学素养探讨[J].中学数学教学参考,2016(4):7-10.
[2]罗增儒.从数学知识的传授到数学素养的生成[J].中学数学教学参考,2016(7):2-7.

