基于SIR模型的新冠肺炎疫情传播预测分析
张艳霞,李 进
(安徽工业大学a.数理科学与工程学院;b.计算机科学与工程学院,安徽马鞍山243032)
传染病不仅严重威胁人们的生命安全,也严重阻碍人类社会的发展,如古希腊的天花疫情、古罗马及欧洲的鼠疫与霍乱、2003年我国SARS病毒非典型肺炎及2014年非洲埃博拉病疫情等。2019年12月30日我国出现新型冠状病毒肺炎(简称新冠肺炎)疫情,自疫情开始30 d内新冠肺炎确诊人数就超过非典型肺炎的确诊人数。至2月23日,全国共累计报告确诊的新冠肺炎病例77 150例,共累计死亡病例2 592例。其中,湖北省累计确诊的病例64 287例,累计死亡病例2 495例,在全国累计确诊的病例中湖北省占相当高的比例[1]。因此,及时预测分析新冠肺炎疫情传播趋势对于疫情的有效防控与防治具有重要意义。
科研工作者常采用数学模型推导传染病不蔓延条件、预测分析传染病流行与受感染者变化趋势等,据此制定相应的防控办法。现有传染病预测模型有Malthus模型,简称S模型[2],S模型随着时间的延长最终未感染者均变成感染者,预测结果不符合实际,主要原因是有效接触的人若是感染者不能使感染者数增加,须区分感染者和未感染者。为区分感染者(susceptible)与未感染者(infective),建立了Logistic 模型[3],简称SI 模型,SI模型没有考虑治愈者因素,预测结果也不符合实际情况。对于治愈者没有免疫能力可能再次被感染的情况,多采用SIS模型(susceptible-infective-susceptible)。对于治愈者有免疫能力不再被感染,多采用经典的SIR模型(susceptible-infective-removed)[2-3],经典的SIR模型结构简单、可操作性强,适用于描述疾病发展的整体趋势,因而得到广泛应用。如文献[4-5]中利用经典SIR模型对2003年北京市SARS疫情进行了分析,从整体上描述了疫情发展的趋势及疾病传播的一般规律,但该模型忽略了部分细节因素,如没考虑传染病死亡者。鉴于此,文中针对新冠肺炎疫情传播状况,考虑新冠肺炎死亡者因素,对经典的SIR模型进行改进,推导出新型冠状肺炎疫情不蔓延的条件,采用改进的SIR模型对新冠肺炎疫情进行预测分析,以期为新冠肺炎疫情防控与防治措施的制定提供数据参考。
1 SIR模型的改进
经典的SIR模型把人群分为三类,即感染者、未感染者、治愈者。文中针对新冠肺炎疫情传播状况,考虑新冠肺炎死亡者因素,改进经典的SIR模型,将人群分为未感染新冠肺炎者(未感染者)、新冠肺炎者(感染者或病人)、新冠肺炎治愈者(治愈者)、新冠肺炎病死亡者(死亡者),但不考虑出生和自然死亡因素。
1.1 模型假设
1)设未感染者、感染者、治愈者、死亡者所占比例分别为s(t),y(t),r(t),q(t),这里s(t)+y(t)+r(t)+q(t)=1;
2)设病人的日接触率为λ,即每个病人每天有效接触的平均人数,日治愈率为μ(治愈人数占病人总数的比例),传染病死亡率为m,即死亡人数占病人总数的比例;
3)假设人群中总人数N不变,不考虑出生和自然死亡因素。
1.2 模型建立
首先给时间t一个增量Δt,考虑在Δt内增加的病人数及减少的未感染者、治愈者及死亡者人数,则Δt内增加的病人数为

Δt内减少的未感染者

Δt内减少的治愈者

Δt内减少的死亡者

将式(1)~(4)两端除以Δt,消去N,取极限得

假设初始条件为y(0)=y0,s(0)=s0,r(0)=r0,q(0)=q0,y0+s0≈1,由此不能计算出模型(5)的解析解。这里只分析s(t),q(t),r(t)随时间t的变化关系。
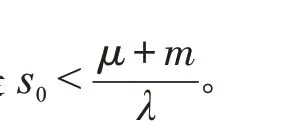
证明 设D(s,y)={(s,y)|s≥0,y≥0,s+y≤1},在D(s,y)上分析y(t)随s(t)的变化趋势。式(5)中前两式相除可得

解微分方程(6),再由初始条件y(0)=y0可得

(7)式两端对s求导得

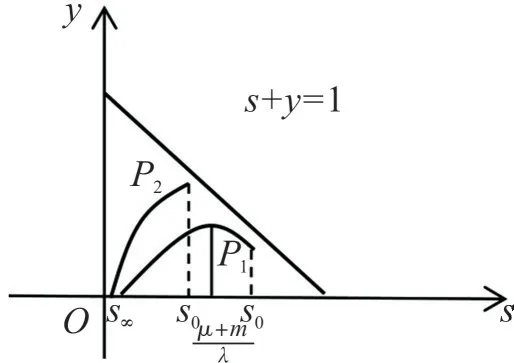
图1 传染病扩散示意图Fig.1 Schematic diagram of spread of infectious diseases
(1)在死亡率m不变的情况下,提高治愈率μ,降低日接触率λ;
(2)在死亡率m降低的情况下,更要提高治愈率μ,降低日接触率λ;
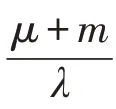
2)降低s0,r0=1-s0-y0-q0,在y0,q0不变的情况下,降低s0,即提高r0,也即提高全民的免疫能力。
由以上分析可得出有效防控防治新冠肺炎疫情不扩散的措施:全民相对隔离,即少出门、戴口罩、早发现、早隔离,尤其是绝对隔离病人降低日接触率;勤洗手、多通风、锻炼身体,提高卫生条件和免疫力。
2 新冠肺炎疫情传播的预测分析
2.1 数据的选取与处理
实证选取数据总人数N=60 000 000,以2020年1月23日国家卫健委官网发布的新冠肺炎数据作为未感染者比例r(t)、s(t)、感染者比例y(t)、治愈者比例r(t)、治愈者比例r(t)的初始值,即s(0),y(0),r(0),q(0)分别为0.999 976,0.000 014,0.000 000 6,0.000 000 4。根据2月1日至2月8日国家卫健委官网发布的实际数据,可知2月1日至2月8日的平均治愈率为0.042 386,平均死亡率为0.022 778。由此赋值日治愈率μ=0.042 386,死亡率m=0.022 778,预测天数t=180 d。根据改进的SIR 模型方程(5),采用龙格库塔法编程等数值模拟新冠肺炎疫情传播,预测疫情的发展趋势。
2.2 模拟结果与分析
2.2.1 假设病人的日接触率λ=0.3
假设病人的日接触率λ=0.3,根据改进的SIR模型方程(5),采用MATLAB 软件及龙格库塔法编程预测新冠肺炎疫情自2020年1月23日起180 d内的发展趋势,结果分别如图2,3。
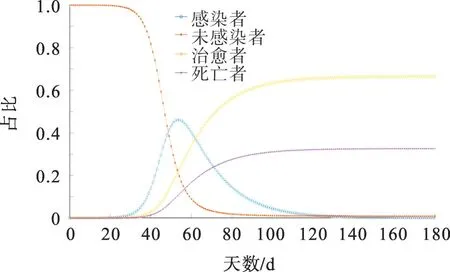
图2 λ=0.3 改进SIR模型的MATLAB曲线Fig.2 MATLAB curves of improved SIR model with λ=0.3

图3 λ=0.3 改进SIR模型的龙格库塔法曲线Fig.3 Runge Kutta curves of improved SIR model with λ=0.3
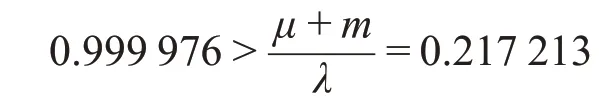
表1为λ= 0.3 时,采用龙格库塔法模拟计算的新冠肺炎疫情自1 月23 日起第10,20,30 d 未感染者、感染者、治愈者、死亡者的比例。根据表1 可计算出:t=10 d即2月2日感染者、治愈者、死亡者的人数分别为7 078,1 152,571 人;t=20 d 即2 月12 日感染者、治愈者、死亡者分别为75 214,13 360,6 556人。而国家卫健委官网显示[1]:2月2日感染者、治愈者、死亡者的人数分别为17 205,475,361 人;2 月12 日感染者、治愈者、死亡者的人数分别为59 804,5 911,1 367人。对比模拟与官网显示数据可发现:1月23日至2月2日,感染者人数的计算值比实际值小,说明1月23日至2月2日病人的日接触率大于0.3;1月23日至2月12日,感染者人数的计算值比实际值大,说明1月23日至2月12日病人的日接触率小于0.3。
由上述分析可推断,1月23日至2月2日病人的日接触率大于0.3,后面20 d病人的日接触率有所降低。若病人的日接触率不降低,从图3可看出感染者比例的最大值较大,即感染者人数较多,这与实际数据不相符,故进一步降低病人的日接触率λ进模拟。
2.2.2 假设病人的日接触率λ=0.2
假设λ=0.2 根据改进的SIR模型方程(5),采用龙格库塔法编程得出未感染者比例s(t),感染者比例y(t)、治愈者比例r(t)、死亡者比例q(t)随时间变化的关系,结果如图4。

表1 λ=0.3,3个时间节点的未感染者、感染者、治愈者、死亡者的比例Tab.1 Proportion of uninfected,infected,cured and dead people in three time nodes with λ=0.3
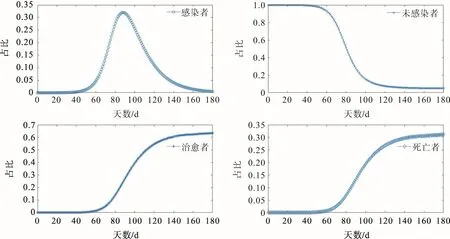
图4 λ=0.2 改进SIR模型的龙格库塔法曲线Fig.4 Runge Kutta curves of improved SIR model with λ=0.2
从图4可看出,感染者比例最大值约为0.32,治愈者与死亡者比例最终分别趋于0.63,0.31。对比图3,4可看出,进一步降低日接触率后,感染者比例y(t)的最大值明显降低,最大值达到的时间推后。由于日接触率的降低,感染的机会变小,即传播速度变慢,因此达到最大值的时间推后,模拟情况符合符合实际情况。
根据改进的SIR 模型方程(5),λ=0.2 时,采用龙格库塔法计算的新冠肺炎疫情自1 月23 日起的第10,20,30 d 未感染者、感染者、治愈者与死亡者的比例,结果如表2。根据表2 可计算出t=10,20,30 d 时的感染者、治愈者与死亡者人数,即2 月2,12,22 日感染者的人数分别为2 878,11 304,44 359人,治愈者人数分别为667,3 278,13 527人,死亡者人数分别为333,1 613,6 637 人。上述计算值小于国家卫健委官网显示的感染者、治愈者、死亡者的数值,说明从1月23日至2月22日内日接触率大于0.2。若日接触率不降低,始终是0.2,感染者比例的最大值为0.320 027,即感染者的最大人数仍然很多,因此需进一降低日接触率。
2.2.3 假设病人的日接触率λ=0.15
假设λ=0.2,利用龙格库塔法编程求解模型方程(5),得出未感染者、感染者、治愈者与死亡者的比例随时间变化的关系,结果如图5。
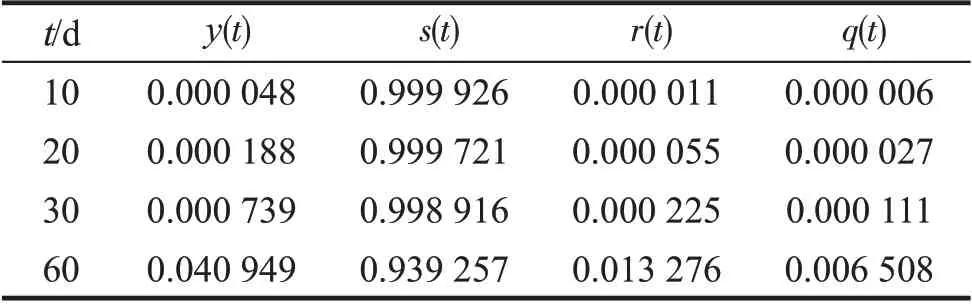
表2 λ=0.2,3个时间节点未感染者、感染者、治愈者、死亡者比例Tab.2 Proportion of uninfected,infected,cured and dead people in three time nodes with λ=0.2
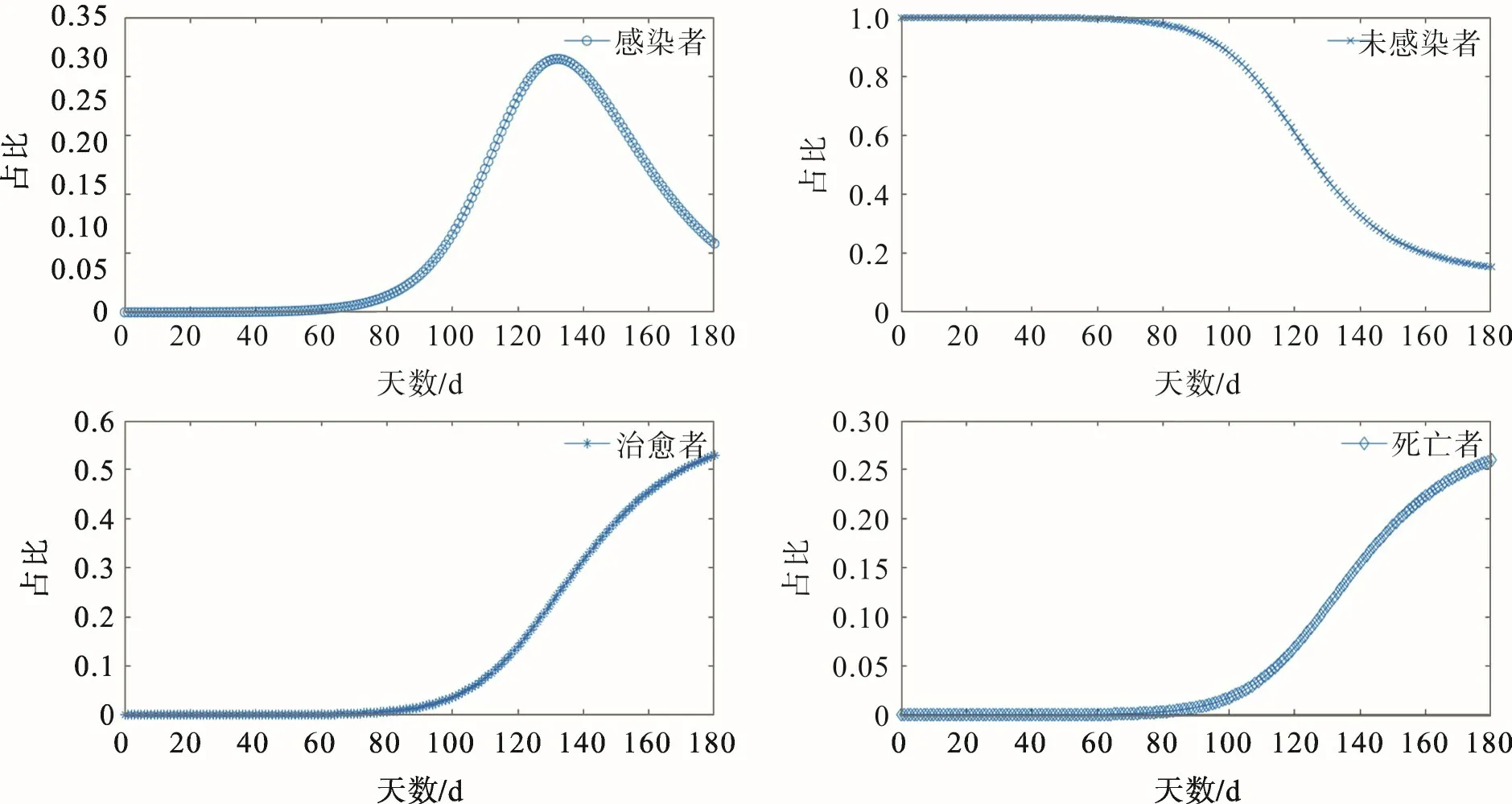
图5 λ=0.15 改进SIR模型的龙格库塔法曲线Fig.5 Runge Kutta curves of improved SIR model with λ=0.15
2.2.4 假设病人的日接触率λ=0.10
假设λ=0.10,利用龙格库塔法编程求解模型方程(5),得出未感染者、感染者、治愈者与死亡者的比例随时间变化的关系,结果如图6。

图6 λ=0.1 改进SIR模型的龙格库塔法曲线Fig.6 Runge Kutta curves of improved SIR model with λ=0.1
从图6可看出,感染者比例y(t)、治愈者比例r(t)、死亡者比例q(t)随时间变化的曲线形状及其最大值都很接近,当t=180 d时,y(t)最终趋于0.01,r(t)最终趋于0.012,q(t)最终趋于0.006。对比图2~6可发现,随着病人日接触率的降低,感染者比例的最大值逐渐降低,取得最大值的时间逐渐往后推移。由于病人日接触率的降低,感染机会变小,即传播速度变慢,因此达到最大值的时间推后,但最大值降低,符合疫情传播实际。
2.2.5 假设病人的日接触率λ=0.05
假设λ=0.05,利用龙格库塔法编程求解模型方程(5),得出未感染者、感染者、治愈者与死亡者的比例随时间变化的关系,结果如图7。

图7 λ=0.05 改进SIR模型的龙格库塔法曲线Fig.7 Runge Kutta curves of improved SIR model with λ=0.05
从图7可看出,感染者比例是一直在下降,此时新冠肺炎疫情没有传播。根据结论2中新冠肺炎疫情不蔓延的条件及2.1中初始值的选取,可得当λ<0.065 163 时,新冠肺炎疫情不再传播。因此严格控制日接触率是最有效的防控新冠肺炎疫情不传播的措施。
3 结 论
考虑传染病死亡者因素,改进经典的SIR 模型,以2020 年1 月23 日公布的新冠肺炎疫情数据作为初始值,根据改进的模型方程,采用龙格库塔法编程模拟预测新冠肺炎疫情的传播趋势,得到如下主要结论:
1)在日接触率取定的情况下预测感染者所占比例的最大值及达到最大值的时间,以及治愈者和死亡者比例的极限值。根据不同的日接触率计算3个时间节点感染者的人数并与实际数据比较,得出1月23日至2月2日的日接触率大于0.3,1月23日至2月22日的日接触率小于0.3且大于0.2。由此验证隔离方法能有效降低日接触率。
2) 推导出新冠肺炎疫情不蔓延的条件,利用这一条件得出在治愈率和死亡率不变的情况下,当λ<0.065 163 时,新冠肺炎病毒疫情不蔓延。由此得出降低日接触率是最有效的防控疫情不再传播的措施,即采取全民相对隔离、少出门、戴口罩、早发现、早隔离、病人绝对隔离等方法,通过勤洗手、多通风、锻炼身体等方式提高人们自身免疫力,从而有效降低日接触率。
3)在新冠肺炎疫情传播初期,采用改进的SIR模型进行预测分析,可为疫情防控防治措施的制定提供有益的参考。因疫情传播实际过程中日接触率、治愈率变化较快,且还有其他因素也在变化,因此改进的SIR模型相对来说还比较理想化,后续还需进一步改进。

