复杂海况下水下拖缆数值分析研究

王冲霄，刘忠乐，文无敌，张志强，赵 苗

(海军工程大学 兵器工程学院，湖北 武汉 430033)

水下拖曳系统在海洋资源勘探、反潜作战、反鱼雷及鱼雷实战指标考核等领域具有广泛的应用，线列阵是水下拖曳系统的一个关键组成部分，其水动力特性将显著影响整个水下航行器系统的快速性、操纵性及稳定性，所以开展水下拖缆的水动力特性研究具有重要的理论意义和工程实用价值[1]。在实际海洋应用中，拖缆难免会受到不同海况下水面波浪的干扰，而这些干扰往往会对拖缆诱饵的模拟效果以及水下航行器的稳定性产生较大影响。目前针对波浪对水下拖缆的影响研究，仅有王飞等[2]采用集中质量法对规则波下的拖缆进行了动力学建模计算，而实际海洋中波浪大多为不同频率和波幅组成的不规则波。针对单向不规则波的建模仿真，目前常用的方法有线性波浪叠加法和线性过滤法两种[3-4]。线性波浪叠加法将海浪视为一个平稳的随机过程，认为其由多个不同周期和随机初相位的余弦波叠加而成[4]。

针对水下拖缆，采用集中质量法，在Huang[5]和王飞[2]的研究基础上，利用线性波浪叠加法和谱分析原理，基于海浪P-M谱，将一组不同频率的组成波叠加起来构成波浪运动模型，从而在水下拖缆的运动模型中成功导入不规则波理论。通过仿真计算得到拖缆的偏移量和张力变化，为拖缆的诱饵模拟效果和水下航行器航行安全性评估提供数据支持。

1 拖缆动力学模型

1.1 控制方程

搭载拖缆的水下拖曳系统如图1所示，取空间固定的系统坐标系O-XYZ，将坐标原点设置在水平面上，以此坐标系为基准，从尾部到拖点将拖缆离散为N段，共N+1个节点。

图1 水下拖缆示意Fig. 1 Sketch of the towing cable

定义欧拉角为θ，φ为拖缆姿态角，对于其上任意第i个节点，采用牛顿运动定律可以得到拖缆的控制方程：

(1)

(2)

式中：I为三阶单位阵；l、σ、μ、ρ、k分别为节点长度、横截面积、拖缆单位质量、流体密度和附加质量系数；下标i+1/2为节点i和节点i+1间对应的物理量，下标i-1/2的意义以此类推。

Fi表示作用于节点i上的所有外力，可表示为：

Fi=Ti+Bi+Gi+FDi+Fwi

(3)

式中：Ti、Bi、Gi、FDi、Fwi分别为作用在节点i上的张力、浮力、重力、流体阻力和波浪干扰力。以下对除波浪干扰力外的所有力列出计算模型，而波浪干扰力则根据谱分析原理推导出。

1) 张力

假设缆索形变在弹性范围内，由胡克定律，可得拖缆张力如下：

ΔTi=Ti+1/2-Ti-1/2

(4)

式中：E为弹性模量，τ为缆长方向的切向量。同理可得Ti-1/2，此处不再列出。

2) 浮力

(5)

3) 重力

Gi=mig

(6)

4) 流体阻力

采用Huang[5]、Ablow[6]等人的方法，将流体阻力取为节点两侧流体阻力一半的和，计算如下：

(7)

式中：d为拖缆直径，U为流场速度，Cn和Cτ为拖缆的法向和切向阻力系数。

1.2 边界条件

1) 拖曳端边界条件

拖曳端边界条件为运动学的连续条件，无相对速率时与水下航行器的位置和速度始终一致，为：

(8)

式中：xs、ys、zs、us、vs、ws分别代表航行器在拖曳端的坐标和速度，为对应时间t的函数。

2) 自由端边界条件

视无拖体的自由端为一节点，运用式(1)的方程，有：

(9)

式中：

(10)

1.3 初始条件

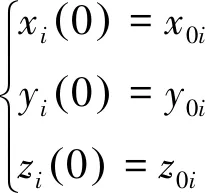
(11)

式中所有右侧量为已给定值，i=N为已给定的首端边界条件。一般采用航行器以固定速度匀速直线航行时拖缆的稳态解为初始条件。

2 基于P-M谱的不规则波模型构建

为简化讨论过程，探讨的波浪模型为一阶深水Stokes波模型， 假设拖缆处于无限水深的环境下，则一阶深水进行波速度势方程为：

(12)

式中：A为波幅；ω为波浪的圆频率，由色散关系ω2=gk可得；g为重力加速度；k为波浪的波数，k=2π/L；L为波长；lw为波浪传播方向上的一维坐标，有：

lw=xsinα+ycosα

(13)

式中：α为浪向角，为波的传播方向与y轴之间的夹角。

海浪运动是一种复杂的随机过程，以确定的函数来描述是非常困难的，谱是描述复杂海浪的有效手段，目前常用的研究方法是利用谱以随机过程来描述海浪。采用Pierson和Moscowitz[7-8]的海浪P-M谱对海浪进行分析，谱密度公式如下：

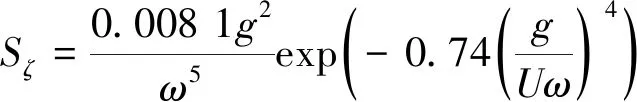
(14)

式中：U代表离海平面19.5 m处的风速。

P-M谱的极值频率为：

(15)

对应平均周期为：

(16)

采用线性波浪叠加法进行研究，由文献[9]，式(12)叠加波的速度势为：

作为县级城市，扬中市智慧城市建设不能盲目跟风，必须从自身实际特点出发，以实际发展需求为导向，进行智慧城市某一领域的重点建设，打造出“智慧扬中”的特色。作为全国闻名的“工程电气岛”和“新能源产业岛”，扬中电力电气产业基地是江苏省首批特色产业基地。近年来扬中正努力实现由电力电气产业基地向智能电气产业基地的跨越，智慧电气小镇建设也取得了重大进展，接下来扬中应着力打造高水平的智慧电气特色小镇，以智慧产业推进扬中智慧城市建设进程。

(17)

式中：下角标n代表第n个组成波的相关特征值，ε为介于0到2π之间的随机相位，M为波浪总数。

以极值频率ω0为中心，把频率范围划分成M个区间，间距为Δωn=ωn-ωn-1，取：

(18)

则波幅An可表示为：

(19)

式中：kn根据色散关系可得，εn由计算机产生随机数(每次不同)可得。

由以上过程，可得由一组叠加波构成的不规则波，其速度势如式(17)所示，略去海流影响，该波浪引起的流场速度uw和加速度aw可表示为：

(20)

改写为标量形式，有：

(21)

(22)

(23)

(24)

参考Morison公式，可认为受流场加速度的影响，拖缆在水中会受到两种作用力：一是流体加速度形成的压力梯度所产生的作用力，另一部分是由相对加速度引起的惯性力。波浪产生的阻力部分以海流形式并入流体阻力中计算，则流场加速度对拖缆的作用力可表示为：

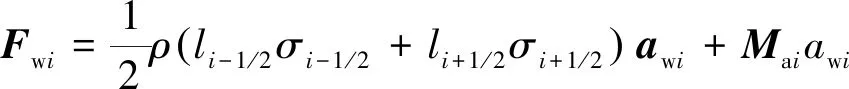
(25)

将式(25)代入式(3)中，即可进行数值求解。

3 仿真结果与分析

3.1 数值求解

通过联立控制方程(1)和边界条件(9)、(10)，以及速度的微分定义v=dx/dt可得到完整的一阶微分方程组，共有6N个方程：

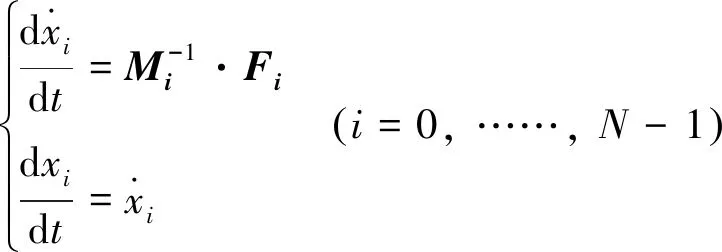
(26)

采用的算例参数如表1所示。

表1 拖缆参数Tab. 1 Parameters of towing cable

引导缆和拖缆的附加质量系数取1.0，离散为130段，即Δs取1 m，依照稳定条件，时间步长Δt取为1 ms。针对4、5、6级三种复杂海况环境对应的海面征象，选取蒲福风级表作为海浪等级的参考依据，可得出相对应的海面风级[11]，如表2所示。

表2 蒲福风级表Tab. 2 Beaufort wind scale

海面风速U分别取各级海况对应风速的最大值，波浪总数M=200，航行器设置为水下15 m深处，航速vy=2 m/s。各级海况下风速和不规则波的计算参数如表3所示。

表3 各级海况下不规则波计算参数Tab. 3 Calculating parameters of irregular waves under various sea conditions

3.2 拖缆的稳态解

图2所示为航行器在航速为2 m/s航行时，拖缆的稳态缆型和拖曳端张力曲线，由仿真结果可知，尾部拖缆稳定在z=-15.352 3 m处，拖曳端处张力T=352.193 9 N。

图2 稳态缆形和拖曳端张力曲线Fig. 2 Stable cable shape and tension curve of towline

3.3 拖缆在不同海况下数值解

将拖缆的稳态解作为初始条件，分别对三种海况下拖缆的形状和拖曳端张力进行仿真。仿真结果表明：随着海况等级的提高，叠加波的频率范围逐渐降低，拖缆的垂向振动偏移量明显加大，且其波动周期接近不规则波的平均周期T0，相比4级海况，5级、6级海况下偏移量最大值分别增大117.14%和171.43%；同样，拖曳端张力亦随着海况等级的提高，在原稳定值附近的波动变化也明显加大，波动周期亦接近不规则波的平均周期，相比4级海况，5级、6级海况下张力最大值分别增大2.1%和6.85%。从整体而言，海况等级越高，拖缆和张力的不稳定性越大，其波动周期也越大，这一点符合日常观察经验。

下面仅给出4级、5级、6级三种海况下，浪向角为0°时，时间t在450～500 s区间内达到稳定后，拖缆自由端(i=0)相对稳态解的垂向偏移量变化曲线和拖曳端(i=N-1/2)的张力变化曲线，如图3、图4、图5所示。

图3 4级海况下垂向偏移量(节点i=0，时间450～500 s)和拖点处张力变化曲线Fig. 3 Vertical offset of grade 4 sea condition(Node i=0,time 450～500 s) and tension curve at drag point

图4 5级海况下垂向偏移量(节点i=0，时间450～500 s)和拖点处张力变化曲线Fig. 4 Vertical offset of grade 5 sea condition(Node i=0,time 450～500 s) and tension curve at drag point

图5 6级海况下垂向偏移量(节点i=0，时间450～500 s)和拖点处张力变化曲线Fig. 5 Vertical offset of grade 6 sea condition(Node i=0,time 450～500 s) and tension curve at drag point

3.4 拖缆在不同浪向角下的数值解

海况等级取5级，浪向角分别取0°、15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°、180°，对拖缆在不同浪向角下的形状和拖曳端张力进行数值仿真。仿真结果表明：在不规则波的作用下，拖缆以接近波的平均周期T0做近似简谐振动；在横向和垂向均产生一个偏移量，横向偏移在浪向角为75°和105°附近时最大，在0°和180°时最小，均为0 m；垂向偏移在0°、15°、165°、180°附近时最大，在90°附近时最小；拖曳端张力在45°和135°附近波动最大，在90°附近波动最小；就整体而言，拖曳端张力始终在稳定值附近波动，其波动周期同样接近不规则叠加波的均值T0。

下面给出不同浪向角下，时间t在450～500 s的区间内基本达到稳定且上浮速度较慢后，拖缆自由端(i=0)相对稳态解的横向和垂向偏移量变化曲线和拖点(i=N-1/2)的张力变化曲线，如图6、图7所示。

图6 不同浪向角下拖缆自由端运动曲线Fig. 6 Motion curve of free end of towing cable at different wave direction angles

图7 不同浪向角拖点处张力变化曲线Fig. 7 Tension curve at drag point at different wave direction angles

4 结 语

1) 通过集中质量法和谱分析理论建立了水下拖缆在复杂海况下的动力学模型，针对实例进行了仿真计算。结果显示拖缆在复杂海况的不规则波作用下，会产生一定的垂向偏移量，总体会有上浮；随着海况等级的增加，叠加波的频率范围逐渐降低，缆绳张力的波动也会更加剧烈，且垂向偏移量和张力的波动周期也会增加，总体接近于叠加波的平均周期。

2) 通过对不规则波作用下不同浪向角的拖缆仿真计算，发现其波动规律与规则波作用下类似，但也具有不规则波的特点，从整体上看做近似的简谐振动，且波动周期同样接近叠加波的平均周期。