焊接所致力学性能不均匀性对卷管法安装管道完整性影响
李 英,李婧一
(天津大学 建筑工程学院 水利工程仿真与安全国家重点实验室,天津 300350)
卷管铺设有两种形式:水平式与竖直式。卷管法中,管道先在陆地上进行预制接长,然后通过卷筒进行上卷退卷。卷管法可以实现20英寸直径以下管道的高效安装,因此被广泛应用于深水油气管道安装。
卷管安装过程中,管道受力过程十分复杂,会发生数次循环往复的弯曲,塑性变形将对管道结构性能和环缝焊接处的疲劳寿命产生影响。因此,研究人员对卷管铺管中管道的材料性能、载荷效应、应变、椭圆度和局部屈曲等问题进行了研究。Hauch和Bai[1]研究了金属管道的抗弯能力,给出了在压力、纵向力和弯曲的组合载荷下管道极限承载能力的解析解,导出的方程可用于具有各向同性以及各向异性的高强度管道材料。Corana等[2]研究了轴向弯曲下薄壁管道屈曲的形成过程,并基于瞬时变形理论对管道局部屈曲进行预测,研究了管道材料特性的变化。基于非线性随动强化材料,Chatzopoulou等[3]通过开展有限元分析,研究了卷管过程中循环弯曲载荷对厚壁无缝管道力学性能的影响,结果表明在卷管完成后管道材料性能表现为各向异性,且横截面变形将导致管道力学抵抗性能降低。Mirzaee和Bastola[4]通过有限元方法模拟大塑性变形条件下管道残余应力的分布,对卷管安装中管道残余焊接应力的分布进行预测。Karamanos 和Tassoulas[5]研究表明铺管期间,管道下垂段受到高外压时会发生显著弯曲,将加剧管道横截面椭圆化,导致管道坍塌。Karjadi等[6]对不同管径和壁厚的管道进行了一系列弯曲试验和有限元分析,获得卷管期间管道的残余椭圆度并进行管道局部屈曲校核。白勇等[7]通过与J-lay法的类比,简化了卷管铺管水下段的稳定性问题,并基于悬链线和小变形梁理论给出了应用卷管铺管法铺设柔性管的数值计算方法。为校直卷管铺设中管道的塑性弯曲变形,王立权等[8]建立了一种基于弹塑性理论的校直模型,研究了管道材料参数和几何参数对校直曲率的影响程度。张九菊等[9]基于应变能法和Ritz 法对海管椭圆度进行理论推导求解,并得到了椭圆度随海管几何参数变化的规律。
在管道生产过程中,通常需要对管材进行热焊、热轧,导致管道形成焊缝缺陷,同时管道性能将产生变化。此前已有针对焊缝缺陷对卷管铺管影响的研究,Wastberg等[10]研究了卷管安装过程中焊缝缺陷对管道性能的影响。李清泉和杨和振[11]对卷管铺管过程进行有限元模拟并进行多轴疲劳分析,探讨了未焊透和未融合两种焊缝缺陷对管道材料特性的影响。另外,焊缝的裂纹可使管道产生应力集中,使管道在卷管铺设过程中承受弯曲载荷的能力大幅降低,张九菊等[12]研究了具有不同裂纹角的管道在弯曲载荷下的变形并对结果数据进行函数拟合,得到了有裂纹海管的极限弯曲载荷表达式。
管道在环形焊缝处及其邻域的热影响区管段存在力学性能不均匀性,且由于管道在卷管安装期间受到复杂的联合载荷,因此在卷管安装管道设计中应该充分研究焊接引起的不均匀性对于管道完整性的影响。首先将对卷管铺管设计中数值模拟选用的材料模型进行探讨,并以此为基础针对焊接所致管道力学性能不均匀性的缺陷对卷管安装中管道性能的影响进行研究。
1 管道材料本构模型
在进行管道非弹性力学行为的数值模拟时,一般采用各向同性硬化模型模拟管道的材料特性,但管道在承受循环弯曲载荷后,其材料性能将由各向同性变为各向异性,因此应选取合理的数值分析材料模型以获得管道在卷管过程中的真实力学响应。为此分别使用各向同性硬化材料模型及非线性材料模型(选取Ramberg-Osgood材料模型)进行卷管铺管仿真模拟,通过对比二者的有限元分析结果,选取适宜卷管安装设计的数值分析材料模型作为研究管道力学性能不均匀性影响的基础。
Ramberg-Osgood材料模型的应力-应变关系为:

图1 应力-应变关系Fig. 1 Stress-strain relationship
式中:ε为应变;σ为应力;E为材料弹性模量;σy为材料屈服应力;α和β为材料常数,对于X65钢,α=1.29,β=25.58。
各向同性硬化模型与Ramberg-Osgood材料模型的应力-应变关系如图1所示。图1表明在初始单调加载过程中两种材料模型均与真实实验结果吻合较好。而进入到反向加载阶段后,各向同性材料模型仍通过单调加载所得到的力学响应为材料提供应力-应变关系,导致其值大于材料在滞后响应作用下的真实值。
2 有限元仿真模拟
2.1 有限元模型建立
采用ABAQUS建立非线性三维有限元模型模拟管道上卷及退卷的过程。管道及卷筒结构如图2所示,管道外径D=0.323 9 m,壁厚t=0.019 05 m,卷筒半径R=8.5 m。管道总长s=160 D。为模拟焊接所致的管道力学性能不均匀性并探讨其影响趋势,假定焊接缺陷管段材料屈服应力低于规定屈服强度下限。取长为4D的CD管段定义为焊接缺陷管段,令该管段处材料的屈服应力为X65钢的90%;其余管段为普通管段,管道材料采用X65钢,材料属性见表1和表2。

表1 材料属性Tab. 1 Material properties

表2 两种材料应力-应变关系Tab. 2 Stress-strain relationship for two materials
通过拉伸试验确定材料应力-应变曲线时,考虑试件在拉力作用下原长不断增加的应力-应变曲线称为真实应力-应变曲线,不考虑试件原长变化的应力-应变曲线称为工程应力应变曲线,两者之间的差别在于应变的计算方法不同。真实应变与工程应变转换方程如下:

(2)

(3)
εT=ln(1+ε)
(4)
式中:εT为真实应变,ε为工程应变。
令管道A端与卷筒圆心耦合,卷筒以0.1 rad/s的角速度转动并带动管道上卷及退卷;管道F端仅在垂直方向存在约束,水平方向受恒定回拉力T作用,其中T=0.01T0(T0为管道屈服应力与管道截面积的乘积),如图2所示。管道应用S4 shell单元模拟,将AB管段和EF管段环向划分为32个网格,轴向每长D为一个网格。由于主要研究管道材料性能缺陷引起的应力和变形,故取焊接处前后各3D的管段(BE段)为测试管段,对该段采用更精细的网格划分,环向上仍划分32个网格,轴向每D长划分10个网格,其网格大小为普通管段的1/10。卷筒由解析刚体模拟,卷筒与管道之间定义为面面接触,卷筒面刚度较大为主面,管道面刚度较小为从面,接触刚度恒定,主面可以穿透从面,从面不可以穿透主面。

图2 卷有限元模型Fig. 2 FE model of pipe reeling
2.2 有限元结果对比分析

图3 上卷阶段两种本构模型下的管道曲率Fig. 3 Curvatures under two kinds of constitutive models during reeling
分别使用各向同性硬化模型及Ramberg-Osgood材料模型进行卷管铺管的有限元模拟,提取上卷及退卷阶段管道沿管长s方向上的曲率、等效塑性应变及残余椭圆度。根据管道变形后的节点坐标计算管道曲率k,对其进行标准化后得到上卷阶段管道局部曲率k/k1(其中k1=t/D02),如图3所示,其值可代表卷管期间管道构型的变化。使用各向同性硬化模型进行模拟时管道曲率峰值为2.0左右,采用非线性运动硬化模型所得管道曲率峰值为1.7左右。图4为管道等效塑性应变ε的分布图,图4表明各向同性硬化模型所得的等效塑性应变峰值为0.055左右,非线性模型所得的等效塑性应变峰值为0.046左右。图5为管道椭圆度ΔD/D的分布图,各向同性硬化模型的结果显示上卷完成后管道的残余椭圆度最大值为5.5%左右,而非线性运动硬化模型的结果为4.7%左右。
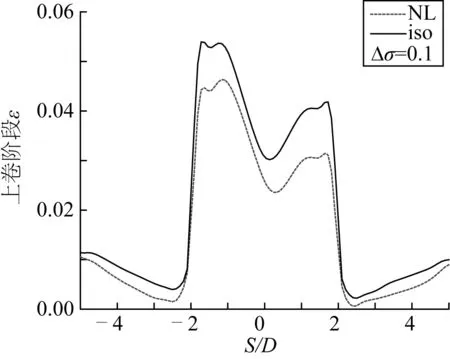
图4 上卷阶段两种本构模型下的管道等效塑性应变Fig. 4 Pipe equivalent plastic strain in two kinds of constitutive models during reeling
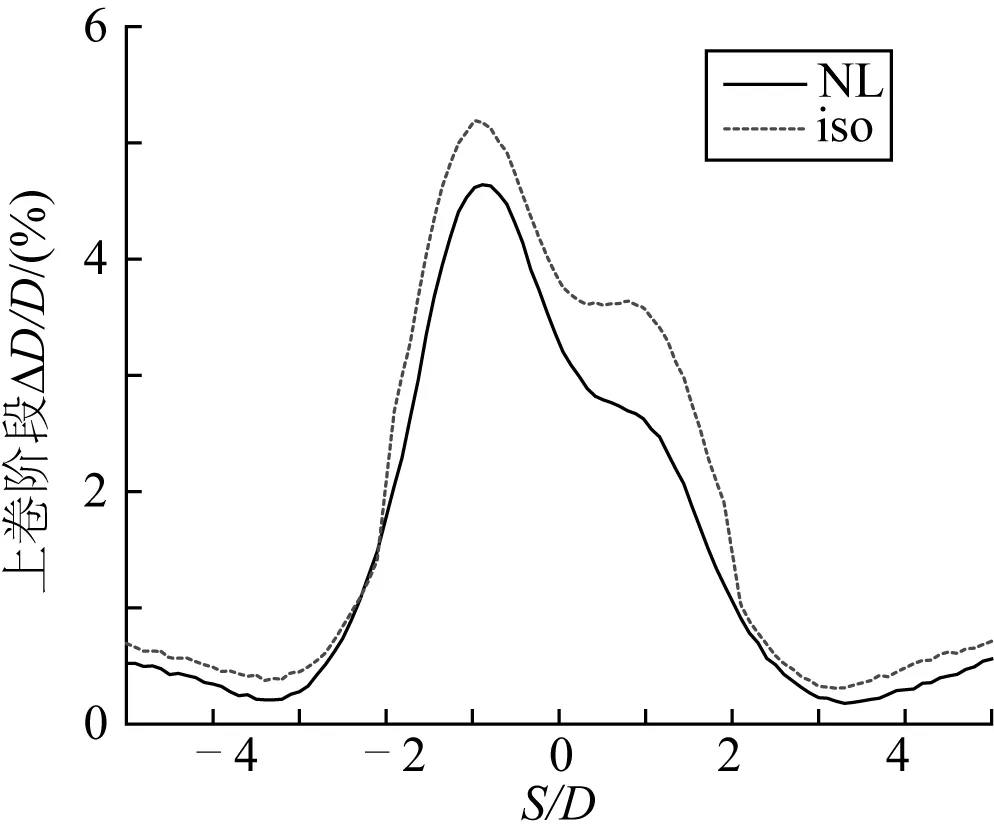
图5 上卷阶段两种本构模型下的管道椭圆度ΔD/DFig. 5 Pipe ovality ΔD/D in two kinds of constitutive models during reeling
另外,各个曲线在力学性能不均匀的管段处均存在明显波动,说明上述两种模型均可模拟由于管道卷曲及管段力学性能不均匀性所引起的局部曲率、残余椭圆度及等效塑性应变沿管长方向的变化,但在上卷阶段各向同性硬化模型所预测的结果均较Ramberg-Osgood本构模型所得的结果稍大,且在管道焊接处及其邻域管段的局部波动也更为明显。但在上卷阶段,两种材料本构模型所得结果的差异并不大,不能准确评估哪种模型能更为真实地模拟管道在卷管安装铺设过程中的力学行为。

图6 退卷阶段两种模型下的管道曲率Fig. 6 Pipe curvatures in two kinds of constitutive models during unreeling
图6为退卷完成后管道的局部曲率。使用Ramberg-Osgood模型分析得到的结果显示退卷阶段管道的局部曲率较上卷阶段有所减小,这是由于管道在退卷过程中被拉直,此时曲率峰值为0.37左右。图7为管道等效塑性应变的对比,图7表明管道等效塑性应变在退卷完成后将会增加,其峰值为0.095左右。图8表明退卷后管道残余椭圆度沿管长的分布情况与曲率及应变相似,其最大值为1.7%左右;但使用各向同性硬化模型模拟所得的结果中,管道的局部曲率、椭圆度及应变均显著增加,其峰值远远大于非线性模型结果曲线的峰值。DNV规范[13]中规定管道椭圆度不可超过3%且管道累积应变不可超过0.3%,故其最大值已大大超过DNV规范所规定的标准值,按其仿真结果管道将在退卷期间发生局部屈曲。总之,在退卷阶段两种模型所得结果之间存在更为显著的差距。

图7 退卷阶段两种模型下的管道等效塑性应变Fig. 7 Pipe equivalent strain in two kinds of constitutive models during unreeling

图8 退卷阶段两种模型下的管道椭圆度ΔD/DFig. 8 Pipe ovality ΔD/D in two kinds of constitutive models during unreeling
上述结果表明,使用各向同性硬化模型对卷管安装中管道的力学行为进行模拟时,将得到管道在反向加载过程中出现失稳的结论,不符合管道在卷管铺管中的实际力学行为;而使用Ramberg-Osgood模型进行模拟所预测的结论更为贴合管道真实的力学行为。如图1所示,这种现象是由于各向同性硬化模型不能真实模拟退卷过程中反向加载阶段管道材料响应的非线性变化,忽略了Bauschinger效应,以致得出不合理的结论。
因此,各向同性硬化模型并不适用于卷管安装管道设计的数值仿真,使用Ramberg-Osgood模型可以较为真实地模拟卷管安装中管道的力学行为。
3 管道力学性能不均匀性对卷管安装的影响分析
应用于海上油气生产的管道材料均按其规定的最小纵向屈服应力进行生产,但在管道生产过程中热机械加工操作如相邻管道的焊接结合等,将导致管道材料的力学性能出现不均匀性,其屈服应力沿管长方向也将存在一定变化。因此,管道焊缝处及其邻域管段的力学性能不均匀性难以避免,在卷管法安装管道设计中必须加以考虑。但由于环焊缝处及其热影响区之间的作用相当复杂,因此将管道力学性能的不均匀性理想化为管道材料屈服应力的显著差异进行研究。
为研究管道在焊接处及其邻域管段存在的力学性能不均匀性对卷管安装过程中结构安全的影响,使用与前述所建模型相同的方式,分别建立四段在焊缝及邻域管段具有不同屈服应力的管段,其屈服应力分别为σ1=0.95σ、σ2=0.90σ、σ3=0.85σ、σ4=0.80σ,并使这四段管段在0.01T0的回拉力水平下进行上卷和退卷。
图9是四种屈服应力下管道沿管长方向局部曲率的变化。图9中焊接处屈服应力为σ1时,管道局部曲率较小,在上卷阶段达到峰值,仅为0.8左右;而屈服应力为σ2时,管道局部曲率稍有增大,最大值为1.6左右,此两种情况下局部曲率的波动均不甚明显。而当屈服应力为σ3和σ4时管道局部曲率在焊接处出现幅度极大的波动,当屈服应力为σ4时甚至跃出纵轴幅值,在退卷完成后管道残余曲率仍然很大,说明此时管道已不能被完全拉直。

图9 四种屈服应力下管道曲率Fig. 9 Pipe curvatures under four kinds of yield stresses
图10为四种屈服应力下管道沿管长方向的等效塑性应变。图10表明四种情况下退卷后管道的等效塑性应变均较上卷阶段有所增加,屈服应力为σ1时,管段最大等效塑性应变值分别为0.04左右,此时管段力学性能不均匀性的影响较小;屈服应力为σ2时,最大值为0.09左右;屈服应力为σ3时,最大值为0.18左右;而屈服应力为σ4时,等效塑性应变峰值大大增加,此时管段于焊缝处发生显著的局部变形。

图10 四种屈服应力下管道的等效塑性应变Fig. 10 Pipe equivalent plastic strain of the pipe under four kinds of yield stresses
图11为四种屈服应力下管道在上卷和退卷过程中的椭圆度。图11表明管道椭圆度变化趋势与局部曲率及等效塑性应变相同。随着焊接处管段屈服应力σ的减小,管道在上卷和退卷完成后的残余椭圆度越来越大。
由此可见,屈服应力为σ1时,焊接处管段力学不均匀性对曲率、应变及椭圆度的影响均很小。屈服应力为σ2时,三组曲线均在管道力学性能不均匀处产生更为明显的波动。而当屈服应力较原始值差值达到0.20σ时,从图12中的管道变形图可以看出管道已产生较为明显的凹陷。显然,在此情况下管道焊缝处的局部弯曲刚度已经下降,导致焊缝处及其邻域管段脱离卷筒,管道局部曲率存在显着波动,同时椭圆度ΔD/D也大大增加,局部等效塑性应变最大值已超过20%。此时管段力学性能不均匀性已大大影响其结构完整性,很可能导致管道在后续服役中出现压溃、破裂等严重破坏现象。

图11 四种屈服应力下管道的椭圆度ΔD/DFig. 11 Pipe ovality ΔD/D under four kinds of yield stresses

图12 屈服应力σ4=0.80σ时管道变形Fig. 12 Pipe deformation when yield stress is 0.80σ
此前Dailey等[14]证明钢柱在焊缝及其热影响区域存在应力集中,Netto等[15]通过原型测试验证钢管在焊缝处易产生局部变形乃至断裂。而本文研究表明钢质管道在焊缝缺陷及其邻域管段存在力学性能不均匀性,将对卷管安装中管道的安全性能产生不良影响,且管道力学性能不均匀性越强,其结构完整性及安全性能越差,与Dailey和Netto等人的研究结论相一致。因此,采用卷管法安装管道对管道的焊接性能有着更高的要求。
4 结 语
由于热加工影响,管道材料性能将在焊缝处及邻域的热影响区管段出现差异,即管道存在力学性能不均匀性。首先采用各向同性硬化材料模型与Ramberg-Osgood材料模型建立ABAQUS有限元模型,进行卷管仿真模拟,通过仿真结果的对比分析,确定卷管安装数值模拟中应选用的合理材料模型。基于此,研究焊接所致的管道力学性能不均匀性对卷管安装的影响,研究结果表明:
1) 在卷管铺设的数值模拟中,使用Ramberg-Osgood模型能够更为真实地模拟管道的力学行为,获得更接近真实值的管道力学响应结果,而使用各向同性硬化模型将导致仿真模拟结果出现严重失真,不宜采用。
2) 焊接所致管道材料力学性能的不均匀性足以对卷管安装管道设计产生影响。该缺陷将造成管道应力出现显著增加,从而导致管道在缺陷处产生较大的局部变形,造成管道出现局部屈曲甚至压溃、破裂,且管道力学性能不均匀性的水平越高,对管道结构完整性造成的不良影响也越大。因此,采用卷管安装的管道应该尽量提高焊接质量,减少焊接不均匀性。

