平台运动激励下钢悬链式立管触地点动态分析

尤岩岩，白兴兰，王孟义

(1. 浙江海洋大学 船舶与机电工程学院，浙江 舟山 316022; 2. 浙江省近海海洋工程技术重点实验室，浙江 舟山 316022)

随着海洋油气开发向深水发展，钢悬链式立管作为连接浮式平台与海底生产系统的关键装备，在湿树开发模式中具有良好的经济性和适应性[1]。SCR顶端以一定的预张力连接浮式平台而悬垂于海水中，另一端连接井口，与海床接触后呈反弯形态，如图1所示，立管常因触地区的应力循环发生疲劳损伤。平台运动是诱发立管动态行为和疲劳损伤的主要因素之一，因此研究平台运动激励下立管触地区的动态行为和疲劳性能，对于准确预测管道的疲劳寿命与评估安全状态至关重要。

由于不同的锚泊形式，平台在风、浪、流作用下具有不同的运动特征，对立管的作用以运动耦合分析为主，如Elosta等[2]运用Orcaflex软件建立SCR与半潜式平台的分析模型，以平台RAOs作为激励条件，研究立管触地区动力响应和疲劳性能相对于不同土参数和沟槽发展的敏感性。Wang等[3]运用DeepC得到平台的动力响应，作为立管顶端响应输入到ABAQUS的立管模型中，并考虑管土作用，开展了立管的整体动力分析。白兴兰等[4-5]考虑平台的惯性力，基于CABLE3D建立了立管与平台的整体分析模型，将二者连接处作为刚臂处理，而忽略了二者之间的相对运动。影响触地区动态行为的另一重要因素是海床刚度模型，目前有三类模型用来模拟土对立管的作用，一是弹簧模型，二是RQ模型[6]，三是AB模型[7]。为了提高计算精度，后两种非线性模型已经被写入商业软件，如Orcaflex、ABAQUS，并广泛应用于立管触地区的动态分析[8-9]，AB模型也被写入CABLE3D程序中，用来分析管土相互作用[10-12]。Shiri等[9]利用非线性海床模型模拟管土相互作用，建立动态分析模型，研究触地区沟槽深度对SCR疲劳寿命的影响。Wang等[13]通过优化分析提出了参数化沟槽模型，并研究了沟槽几何尺寸对触地区疲劳损伤的影响。Elliott等[14-15]运用离心机模型技术开发了管土相互作用的试验系统，考虑流体-立管-海床土的交互作用，揭示沟槽形成及沟槽对触地区疲劳损伤的影响。

图1 钢悬链式立管结构示意[16]Fig. 1 Structural sketch of the SCR

上述研究主要围绕平台平面内的运动，特别是垂荡运动对立管的影响，海床土模型仅考虑竖向作用。本文拟研究平台三维运动激励下立管触地区的动态行为和疲劳分析，包括触地点应力分布、贯入位移和疲劳寿命分布情况等，其中海床竖向作用采用RQ模型的土抗力-埋深曲线，侧向作用采用库伦摩擦“双线”模型，纵向作用表现为接触摩擦力，由土摩擦系数确定。

1 数学模型

1.1 控制方程

基于结构动力学原理，可得浮式平台和立管的运动方程[5]：

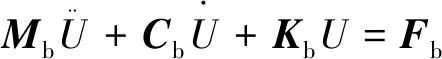
(1)

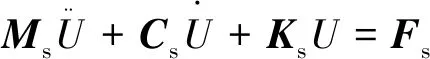
(2)

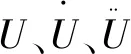
U=Tu

(3)

式中：u、U分别为悬挂点和平台质心的六自由度位移列向量，T为转换矩阵。将平台质心的运动变换得到立管悬挂点处的运动，将式(3)代入式(1)并左乘变换矩阵的转置可得：

(4)

平台运动将带动SCR随之运动，因此，结合式(2)与(4)可得平台与立管的耦合运动方程：

(5)

其中：

1.2 管土作用模型

图2所示为竖向土体抗力与埋深的关系曲线，由Randolph和Quiggin根据模型试验模拟得到[6]，简称为RQ模型，体现了加载-卸载-再加载的管土相互作用过程，其中虚线表示土作用力的边界圈，上边界指土的最大抗力，下边界由最大吸力确定，土抗力和吸力表达式分别为：

Pu(z)=Nc(z/D)su(z)D

(6)

Pu-suc=-fsucPu(z)

(7)

式中：Pu(z)为海床抗力；Pu-suc为海床吸力；Nc(z/D)为承载因子，当z/D≥0.1时，取Nc(z/D)=a(z/D)b，其中a、b分别为模型无量纲系数，与沟槽宽度和立管直径有关，如表1所示；当z/D<0.1时，取Nc=Nc(0.1)(10z/D)1/2，z为贯入深度，D为管直径；fsuc为吸力因子；su为海床土的不排水抗剪强度，与管道的埋深有关，表达式为：

su(z)=su0+ρz

(8)

式中：su0、ρ分别为海床表面不排水抗剪强度和强度梯度。

文献[6]确定了立管与海床接触时三个阶段曲线的数学表达式，图2中横坐标为无量纲参数ζ，通过对贯入深度z进行无量纲化得到：

ζ=z/(D/Kmax)

(9)

式中：Kmax为最大竖向刚度，本文取200。该曲线考虑土刚度退化，表现为上拔后再次贯入时抗力的衰减：

Pmax(z)=ERP(z)PIP(z)

(10)

式中：PIP(z)为初始贯入阶段的抗力，ERP(z)可表示为：

ERP(z)=emin[0,-λrep+(z-zp=0)/(λsuczmax)]

(11)

式中：zmax为最大贯入深度，zp=0指土抗力为零时的最大贯入深度，λsuc为无量纲的吸力衰减因子，λrep为无量纲再贯入系数。

表1 a和b的取值Tab. 1 Value of a and b

图2 典型土抗力-埋深曲线[6]Fig. 2 A typical resistance-penetration curve[6]

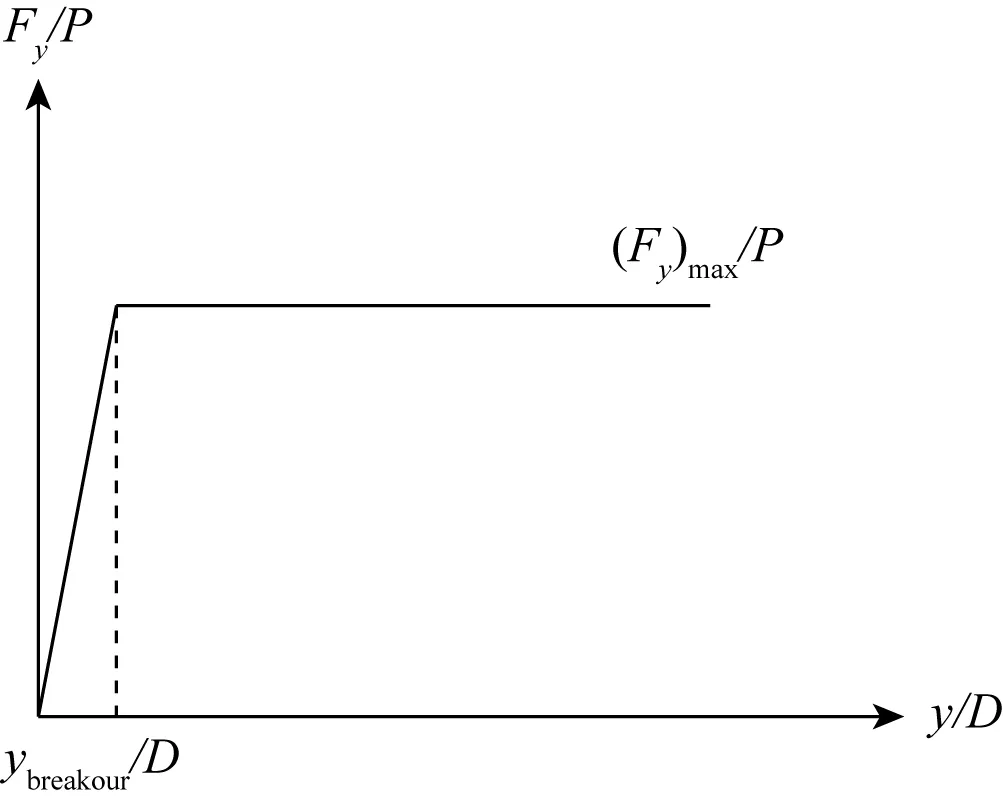
图3 侧向库伦摩擦“双线”模型[17]Fig. 3 Coulomb friction ‘bi-linear’[17] model in lateral direction

图3为侧向库伦摩擦“双线”模型，侧向阻力Fy由竖向土抗力和摩擦系数确定，表达式为[17]：

Fy=-suAy

(12)

式中：y为立管的侧向位移，su为土剪切强度，A为立管侧向与土接触面积。在OrcaFlex的摩擦模型中，侧向库伦摩擦力的变化区间为[-μP,μP]，管道在沟槽中的侧向偏移区间为[-ybreakout,ybreakout]，则ybreakout可表示为：

ybreakout=μP/suA

(13)

式中：μ为摩擦系数，一般在0.2～0.8之间；P为竖向海床土抗力，与海床平面相切。

1.3 疲劳分析

S-N曲线又称为应力-寿命曲线，常用来计算结构的疲劳问题，表达式为[18]：

logN=loga-mlogS

(14)

式中：a、m为由实验确定的经验系数，S为应力幅值，N为与应力幅值对应的循环次数。

通过应力集中系数及厚度修正系数对应力幅值S进行修正，修正后的表达式为：

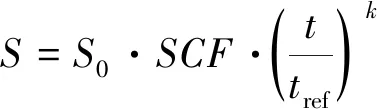
(15)

式中：S0为名义应力幅值；SCF为应力集中系数；t和tref分别为立管的实际壁厚和参考壁厚，参考壁厚取25 mm；k为厚度指权。

2 算例分析

2.1 SCR模型参数

以一根工作水深为1 500 m的SCR为研究对象，具体参数见表2。假设海床是水平的，分别选择线弹性和非线性海床刚度模型，其中竖向非线性海床分低、中和高强度三种类型，海床侧向刚度为11.52 kN/m/m2，吸力因子取0.2，吸力衰减因子取0.5，再贯入系数取0.55，摩擦系数取0.5。

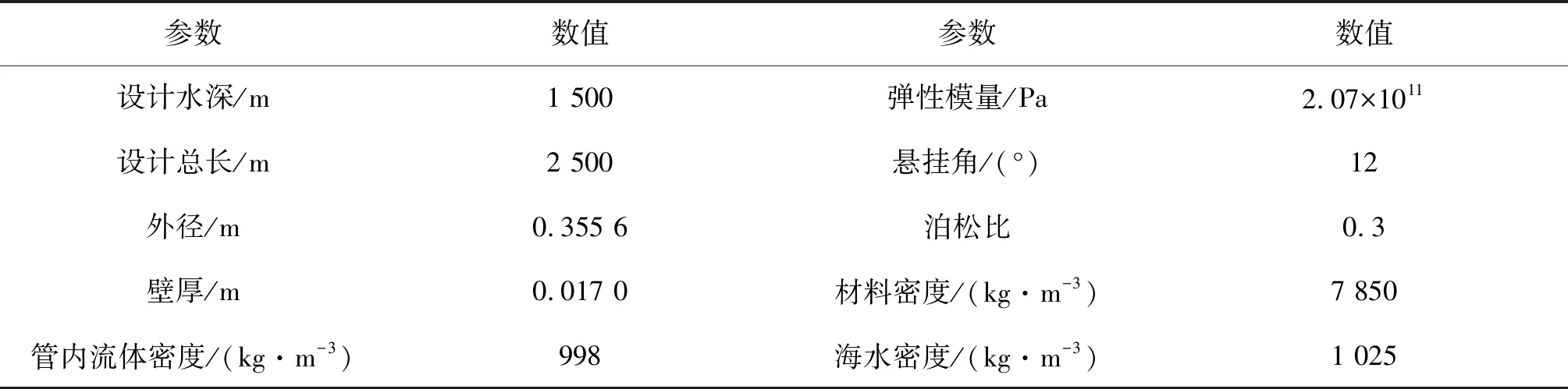
表2 钢悬链式立管模型参数Tab. 2 Model parameters of SCR

2.2 计算工况

主要研究不同平台的激励运动方式、不同强度的海床模型对SCR触地点动态响应和疲劳寿命的影响，共28个工况，选择表3所示的10个计算工况进行对比分析。将立管划分为柔性接头、悬垂段、触地段和流线段四个部分，这与现有研究中仅将平台与SCR的连接作为铰接来处理[12]更符合工程实际。根据需要每段选取的单位长度不同，总共划分为880个单元。平台激励运动周期为16 s，运动幅值为2 m，波高为6 m，波周期为8 s，海面流速为1.07 m/s，每个工况分析时间为300个周期，时间步长为0.02 s。

表3 计算工况Tab. 3 Calculate conditions

3 结果分析与讨论

平台不同形式的运动激励下，分别得到立管触地点的应力、位移以及贯入深度的变化情况；不同的海床强度对触地点动态响应的影响分析；平台运动和海床刚度模型对触地点疲劳寿命的影响程度。

3.1 平台运动的激励

选用非线性低强度海床土，对平台不同运动激励下触地点应力时程曲线、管土作用曲线、触地区贯入深度进行对比分析。

3.1.1 触地点应力

立管触地点循环应力是发生疲劳破坏的关键因素，在LC1～LC7工况作用下，即立管与低强度非线性海床作用，触地点位置在管长1 879 m左右，分别得到图4所示的触地点应力变化对比曲线。结果表明：1)一维运动时，垂荡、纵荡和横荡运动引起的触地点应力幅值分别为49、12.4和2.2 MPa，应力幅值大小是导致立管疲劳损伤的关键因素，可见垂荡运动对立管触地点和顶端动态响应的影响最大，而横荡运动受海床侧向阻力作用，其影响程度最小；2)二维运动激励时，触地点应力幅值分别为47.6、38.8和14.6 MPa，二维耦合运动在一定程度上减弱了垂荡运动引起的动态响应；3)三维运动作用时，触地点应力幅值为38 MPa，相对包含垂荡二维耦合运动有所降低，但远大于纵荡和横荡。

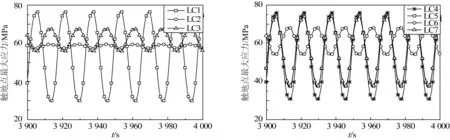
图4 立管触地点应力时程曲线Fig. 4 TDP stress time series under motion excitation of platform

为了验证本文结论，与文献[12]进行了对比分析，如图5所示，选择文献[12]中工况LC2和本文工况LC7，对触地点应力进行对比分析。由对比结果可知：同一海床强度和运动幅值下，垂荡引起的触地点应力幅值比三维运动大4.21 MPa，而且三维运动引起的触地点应力振荡周期明显增加。疲劳损伤的产生原因主要是应力幅值和作用周期，幅值小周期长的循环应力将会降低结构的疲劳损伤，这与本文的结论是吻合的，即三维运动的耦合将会在一定程度上降低SCR触地区的疲劳损伤，因此仅考虑平台的垂荡运动来预测立管的疲劳损伤是不准确的。图6给出了LC7工况下触地点土抗力随相对埋深的变化曲线，体现了图2所示的加载-卸载-再加载的整个作用过程及竖向海床刚度的退化现象，与文献[12]的结果相比，更符合实际作用过程。

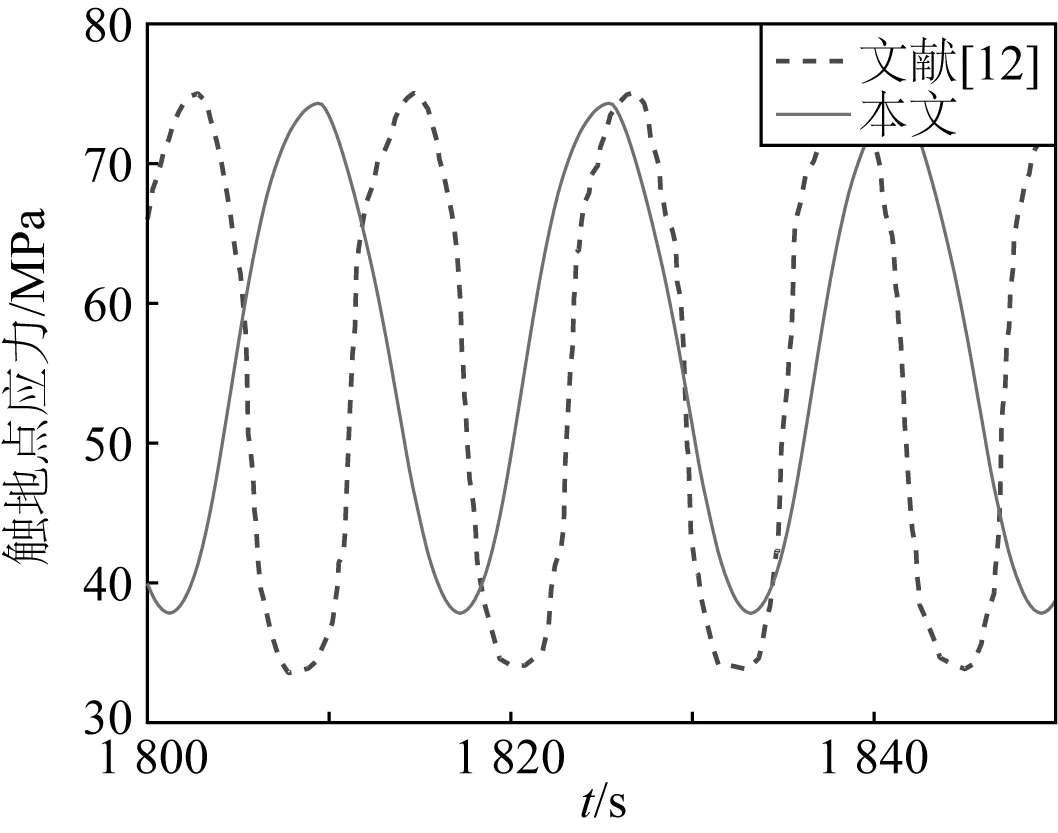
图5 触地应力时程曲线对比Fig. 5 Comparison of the TDP stress time series of SCR

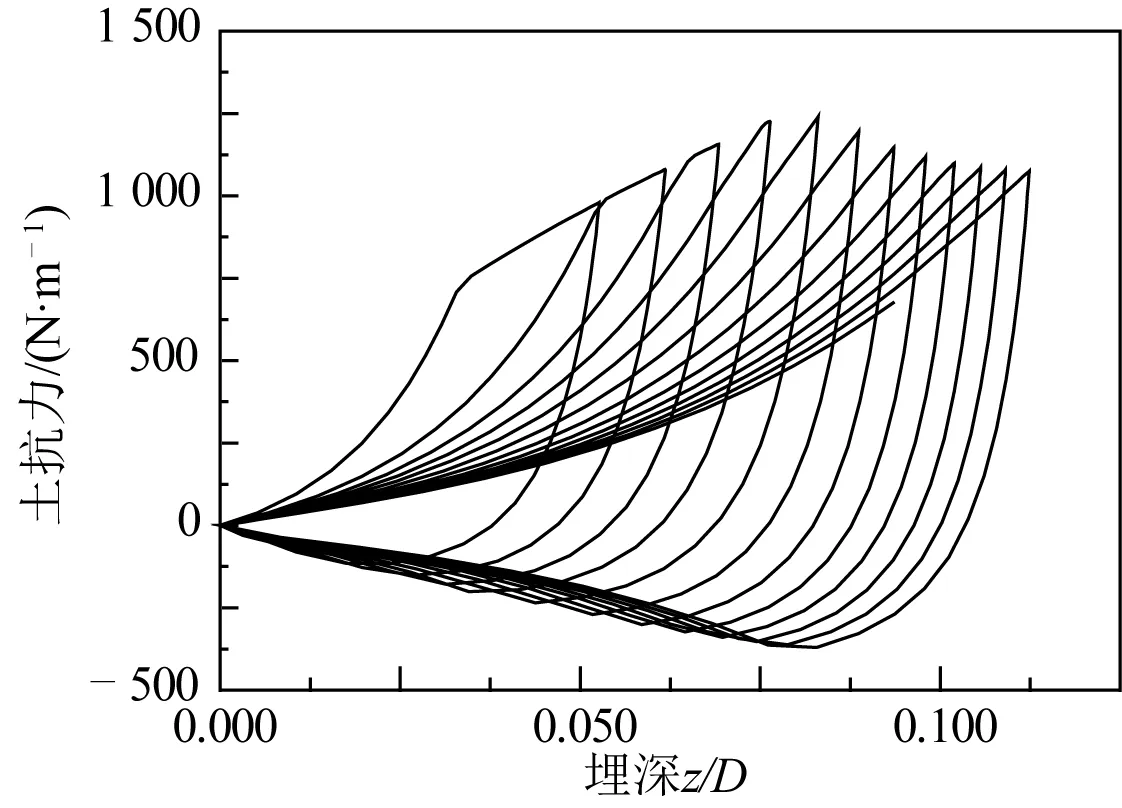
图6 触地点土抗力随相对埋深的变化曲线Fig. 6 Resistance-penetration curve of TDP

3.1.2 立管触地区的最大贯入深度

由于平台运动特别是垂荡运动会引起管土的往复作用，将在海床表面形成沟槽。为研究运动形式对沟槽大小的影响程度，基于非线性低强度海床和侧向海床的阻力作用，分别由一维、二维和三维运动作用300个周期后，获取立管最大贯入深度时的位型图，如图7所示，其中左图为LC1～LC3工况，右图为LC4～LC7工况。表4列出了不同运动方式在海床表面产生的最大贯入深度和相对深度值。由表可知：短期管土作用下，立管的最大贯入深度均小于0.3倍管径，垂荡运动的影响最大，而耦合运动时沟槽深度略有减小。

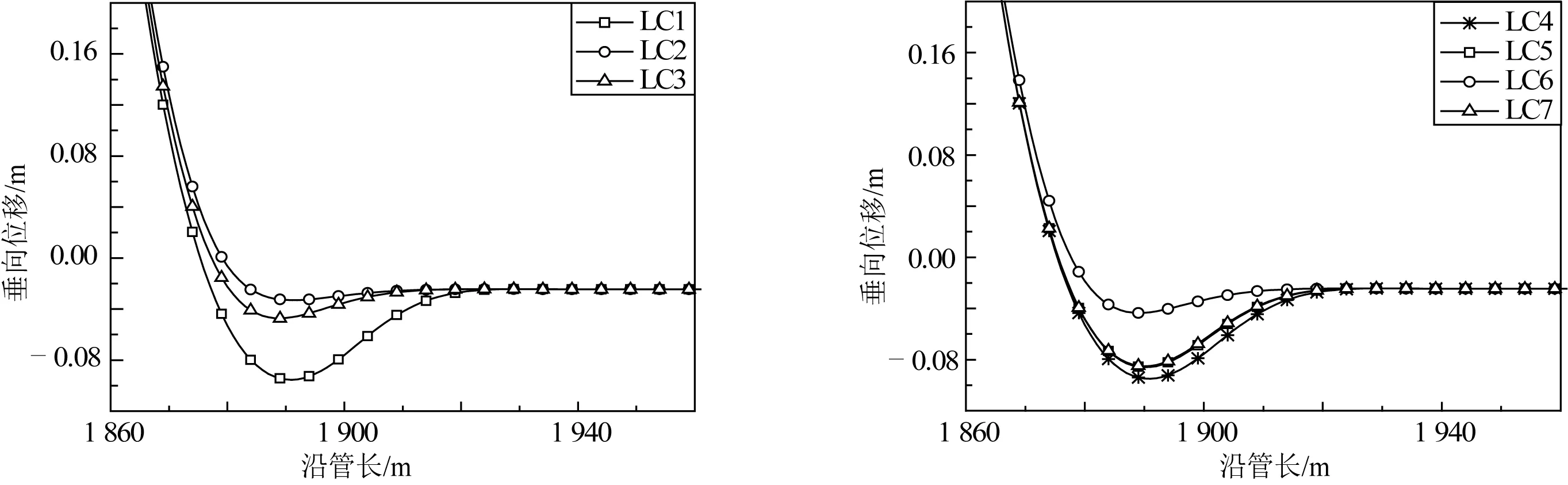
图7 立管最大贯入深度时的位型Fig. 7 Configuration of the maximum penetration depth of riser

表4 不同运动类型下SCR最大贯入深度对比Tab. 4 Comparisons of the maximum penetration depth under different excitation motion

3.2 海床模型的影响

为了研究海床模型对触地区动态行为的影响程度，选择LC7～LC9和LC10工况进行对比分析，其中线弹性海床与低强度非线性海床的强度相当。四种工况下触地点的位置有变化，分别位于管长1 879、1 883、1 884和1 878 m处。图8为四种工况下的触地点应力时程曲线，由图可知：LC7和LC10工况作用下为高应力的低幅值循环，而LC8、LC9工况下为低应力的高幅值循环，幅值大小是引起疲劳损伤的关键因素之一。图9为土抗力随平台运动的时程变化曲线对比，非线性海床模型作用下土抗力变化幅值远大于线弹性海床。而贯入深度则相反，采用线性海床时，立管贯入深度明显较大，如图10所示。图11为立管的弯矩分布图，两种海床模型作用下，得到弯矩分布图基本一致，也验证两种海床模型的强度相当。可见选择线弹性海床模拟海床作用是不准确的，与实际差别较大，特别是触地区的应力和沟槽大小。

图9 立管触地点海床抗力时程曲线Fig. 9 Time series of seabed resistance at TDP

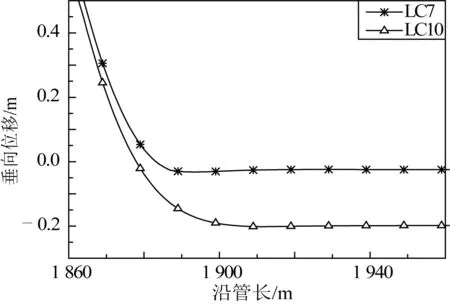
图10 不同海床模型作用下立管触地区贯入深度Fig. 10 Progressive penetration with different seabed models

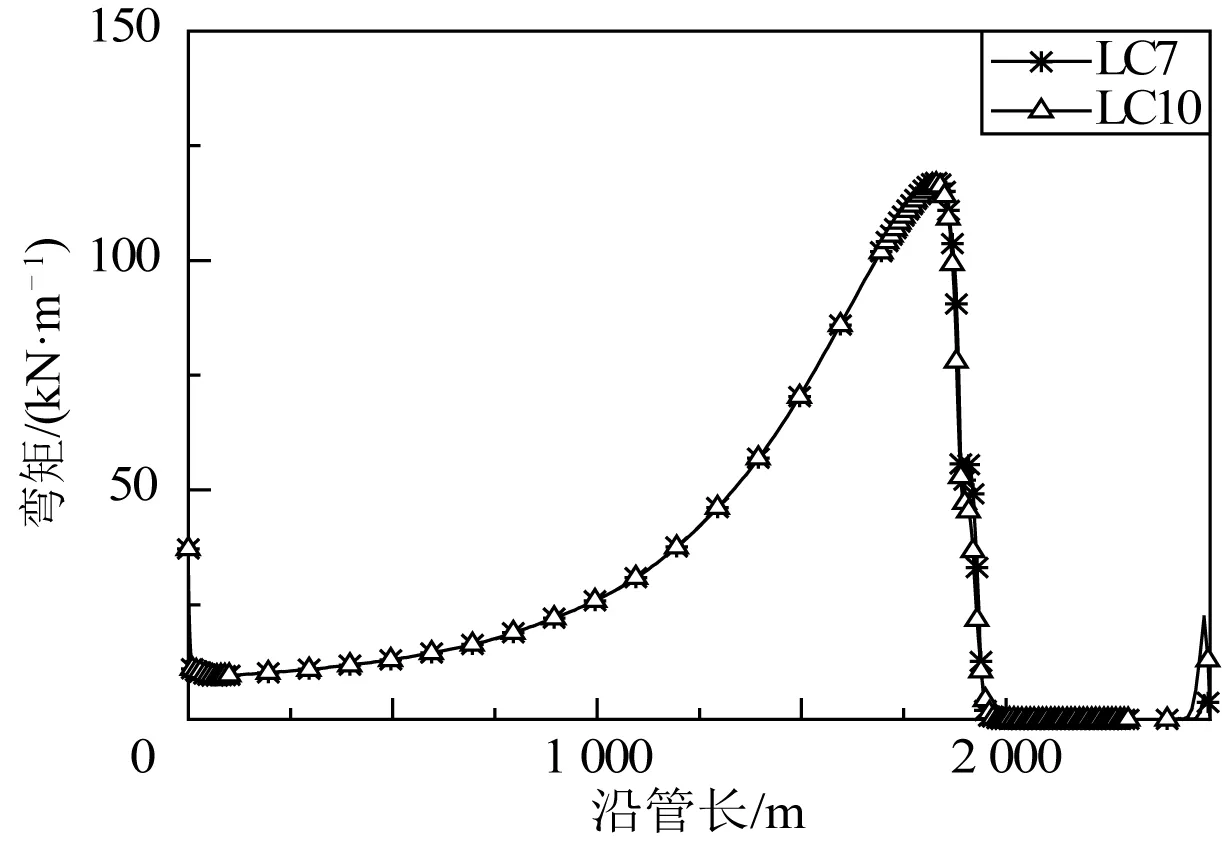
图11 立管弯矩分布Fig. 11 Bending moment distribution of SCR

如图12所示，LC7、LC8和LC9工况下立管触地点侧向位移，随着海床强度的增加，幅值逐渐减小，变化趋势相似；图13为立管触地点竖向位移的时程曲线，随海床强度的增加，位移幅值降低，贯入深度变浅，在接近海床表面时，竖向位移曲线变得比较平坦。

图12 立管触地点侧向位移Fig. 12 Lateral displacement of TDP

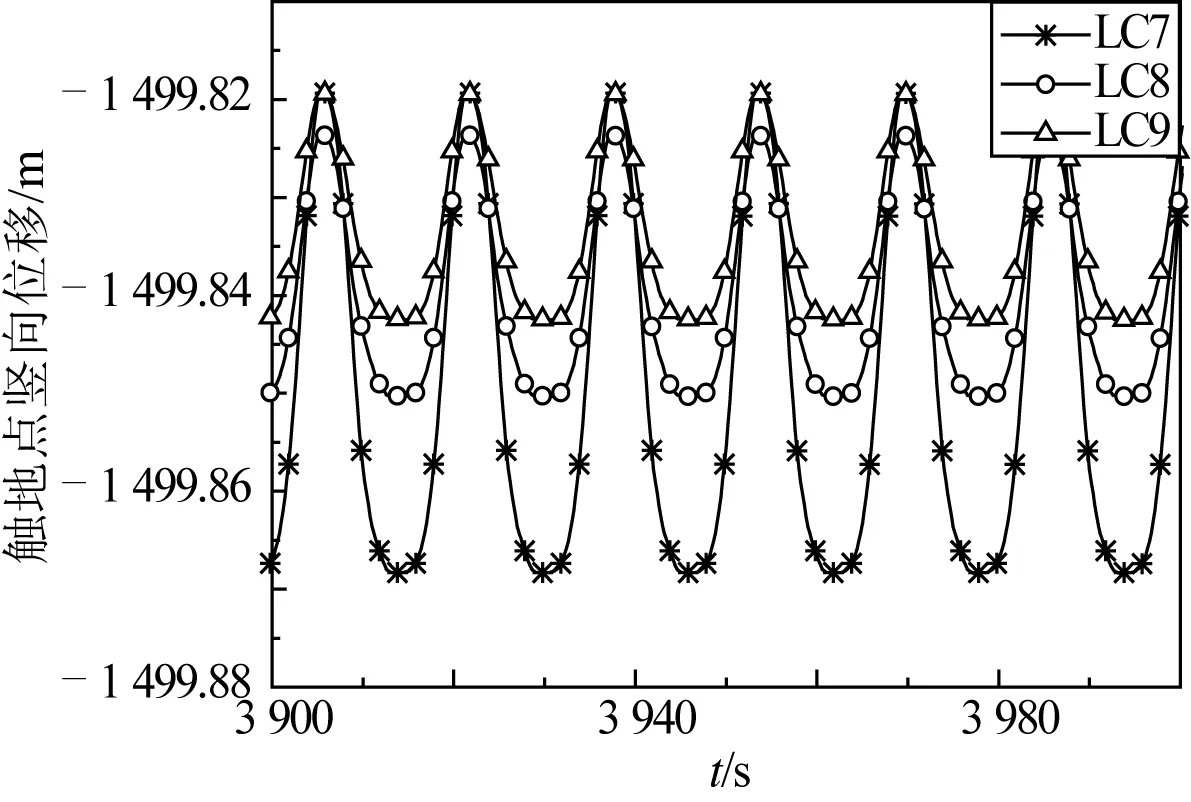
图13 立管触地点竖向位移Fig. 13 Vertical displacement of TDP

3.3 疲劳分析

根据立管的动力响应分析，运用S-N曲线对立管进行疲劳分析，分两种情况：1)研究不同运动形式对立管触地区疲劳寿命的影响，选择LC1和LC4～LC7工况，如图14所示，垂荡作用下立管疲劳寿命最低为76年，也说明垂荡运动是影响立管触地区疲劳寿命的关键因素，而三维运动作用下即LC7工况，立管疲劳寿命则提高至134年，纵荡与横荡运动的影响可忽略；2)研究不同海床模型对立管触地区疲劳寿命分布情况的影响，LC7～LC10工况，如图15所示，高强度非线性海床作用时，立管触地点的疲劳寿命最低为95年。线弹性海床作用下，立管触地区的疲劳寿命明显偏高，因此简化计算时，选用线弹性海床进行模拟管土作用是不安全的。由图示可知，SCR触地点处的疲劳寿命最小，并向两侧迅速增加，该区域控制着立管的使用寿命，应在设计和工程应用中予以加强，其中最小疲劳寿命对比结果见表5。

表5 触地区疲劳寿命对比 Fig. 5 Comparison of fatigue life at TDP of SCR

图14 不同平台运动激励下立管疲劳分布Fig. 14 Fatigue life in TDZ under different excitation motions

图15 不同海床强度下立管疲劳分布Fig. 15 Fatigue life in TDZ under different seabed strength

4 结 语

基于竖向非线性海床模型和侧向库伦摩擦模型，考虑海床土竖向刚度的退化，建立SCR与平台的三维分析模型，研究平台运动、海床刚度模型对SCR触地区动态行为、疲劳损伤的影响，得到如下结论：

1) 平台垂荡运动对立管触地区的应力幅值、贯入位移和疲劳损伤的影响最大，纵荡运动次之，而横荡运动受侧向海床土阻力作用，其影响最小，从最小疲劳寿命看，垂荡运动与纵荡-横荡耦合运动不在一个数量级；

2) 将平台运动耦合之后，在一定程度上使立管触地区的动态响应降低，因此仅考虑垂荡运动的情况偏于保守；

3) 在海床模型中考虑侧向阻力的影响，从计算结果可知，侧向阻力使得平台横荡运动对立管动力响应和疲劳寿命的影响降低，目前以管土竖向作用为主的研究结论同样偏于保守；

4) 海床刚度模型不同，对立管触地区动态响应的影响主要体现在：随海床强度和应力幅值的增加，贯入位移和疲劳寿命逐渐减小。特别是选择线弹性海床与实际差别较大，在贯入位移明显较大时，所得的动态响应较小，疲劳寿命较高，对实际工程不安全。

5) 在竖向非线性海床刚度模型中，考虑了土刚度退化现象，更符合海床软土的实际力学特性。