波浪荷载引起不同埋深管线周围海床响应和液化分析

张 琪， 周香莲， 叶冠林

(上海交通大学 海洋工程国家重点实验室； 土木工程系， 上海 200240)

海底管线是输送石油、天然气等海洋能源的重要结构.在海洋环境中，长期周期性循环的波浪荷载作用会引起管线周围海床内孔压的变化，产生液化现象[1].被液化的海床土会失去对管线的承载力，影响管线的安全稳定.波浪引起海床的液化问题与海床内孔压变化直接相关.近年来，国内外学者们在研究波浪引起海床的响应问题时，对海床做出了不同的假设并提出了单相体模型和刚性多孔介质模型以及Biot流固耦合模型.其中，单相体模型较为简单，不能反映土体的孔压和有效应力[2-3].刚性多孔介质模型可以考虑孔压变化，但是无法得到海床土的变形和应力结果[4].而Biot流固耦合模型可以全面地反映海床土体内部的土体颗粒与孔隙水之间的相互关系[5].Zienkiewicz等[6]提出了Biot流固耦合模型的3种简化理论模型，即准静态模型(QS模型)、部分动力模型(u-p模型)和全动力模型(u-w模型).Zen等[7]研究了一维和二维海床在波浪荷载作用下的孔压分布情况.Gatmiri[8]讨论了海床的各向同性和横观各向异性.Jeng等[9]研究了有限厚度海床在波浪荷载作用下的动力响应，并讨论了波浪的非线性影响.段伦良等[10]分析了各向异性海床波浪荷载作用下的瞬态液化问题.王国才等[11]研究了海床在不同水波和土体物理力学性质参数时的瞬时液化深度，提出了海床抗液化的工程措施.

上述研究仅考虑了自由海床在波浪荷载作用下的响应问题，但是没有考虑海底管线对海床土响应的影响.Jeng等[12]建立了一个二维有限元模型，研究波浪荷载作用下海床内管线周围孔压和土体应力的分布.Wang等[13]采用有限单元法研究了包含管沟的埋管海床在波浪荷载作用下的响应.文峰等[14]采用数值方法研究了埋管海床在波浪和海流共同作用下的响应问题.Zhou等[15]通过试验方法研究了海床内不埋管线和半埋管线情况下的海床土孔压响应.华莹等[16]建立了波浪-海床-管线有限元模型，并分析了随机波作用下多层砂质海床中管线周围土体孔压和有效应力的响应，探讨了海床的液化深度和范围.栾茂田等[17]基于Biot理论和弹性动力学分析了海床与管线之间的相互作用效应，以及海床与管线接触对管线周围海床在波浪荷载作用下响应的影响.邓海峰等[18]分析了随机波作用下海底管线与海床的相互作用问题，探讨了管线与海床土的接触和惯性效应影响.Zhou等[19-20]对波浪荷载作用下管线周围海床土体响应的问题进行数值分析，并分别讨论了椭圆余弦波以及多层海床土情况下的土体响应问题.

目前，由波浪引起的管线周围海床的响应问题以及不同管线埋深情况下海床孔压和有效应力变化规律仍不明确.对此，本文主要研究海底管线及其周围海床在波浪荷载作用下的动态响应和海床液化问题，重点探讨管线埋深对波浪荷载作用下管线周围海床土的孔压、竖向有效应力和液化范围的影响，并对波高、海床土渗透系数和饱和度进行参数分析，为工程设计和安全分析提供参考.

1 数值模型建立与验证

利用u-p模型计算波浪荷载作用下的海床动态响应，考虑土骨架的加速度效应，忽略孔隙水相对于土骨架的加速度.海床土为各向同性的弹性多孔介质，土体骨架的应力应变关系服从胡克定律，孔隙水为可压缩流体且服从达西定律.连续性方程和平衡方程如下：

(1)

(2)

(3)

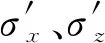
(4)

(5)

(6)

(7)

(8)

式中：Kw为孔隙水的体积模量，一般情况下，Kw=2 GPa；pw0为孔隙水的绝对压力；Sr为海床土的饱和度；Gs为海床土的切变模量；νs为海床土的泊松比.将式(6)～(8)代入式(2)和(3)中，得到由位移和孔压表示的控制方程

(9)

(10)

将u-p模型控制方程通过PDE接口写入COMSOL Multiphysics多场耦合数值软件中，通过有限单元法求解波浪荷载引起管线周围海床土的响应，考虑三维条件中管线的轴向约束作用和相比土体的较大刚度，研究中不考虑管线的受力和变形对土体的影响，因此设定管线为不透水固定边界.波浪引起的管线周围海床液化计算简图如图1所示.其中，D为管线直径，h为水深，d为海床土厚度，e为管线埋深，即管线底部到海床面的距离.边界条件设定如下.

(1) 海床表面(z=0)：将波浪荷载作为孔压边界条件施加于海床表面，即

p=pb=p0cos(kx-ωt)

(11)

式中：pb和p0分别为海床表面波压力和压力幅值；k为波数；ω为角频率.

(2) 海床底部边界(z=-d)：海床底部为不透水边界，且无水平、竖向位移，即

us=ws=∂p/∂z=0

(12)

(3) 海床两侧竖向边界：海床左右两侧的竖向边界为不透水边界，且约束水平位移，即

us=∂p/∂x=0

(13)

(4) 管线与海床接触面：管线与海床之间的接触面为不透水边界，即

∂p/∂n′=0

(14)

式中：n′为管线的径向.

图1 数值模型计算简图Fig.1 Sketch of numerical model

采用Hsu等[21]的波浪引起的自由海床响应解析解对数值模型进行验证.其中，波浪参数[21]为波高H=2 m，周期T=15 s，波长L=311.59 m，h=70 m；海床土参数[21]为弹性模量Es=37.3 MPa，d=25 m，ns=0.3，Sr=1，ρs=1 850 kg/m3，νs=0.333，kz=0.01 m/s.图2为在波浪荷载作用下，数值计算得到的海床土的孔压、竖向有效应力和水平有效应力结果与解析解之间的关系.由图可知，数值结果与理论结果吻合较好，证明了数值模型可以比较精确地研究波浪用下海床响应问题.

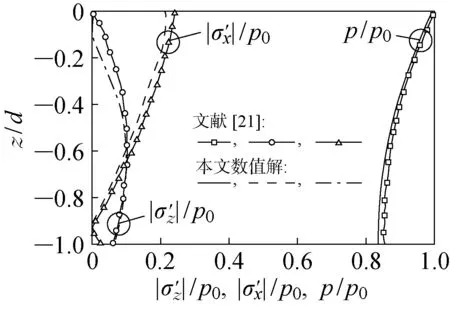
图2 解析解[21]与本文数值解对比Fig.2 Comparison of previous analytical solutions[21] and numerical results

2 管线周围海床土孔压响应和液化分析

在研究波浪荷载引起的埋管海床的响应问题时，需要将管线的三维问题简化为二维问题，这是由于管线周围的海床土在波浪荷载作用下沿管线轴向的响应基本相同.考虑e=D，1.5D，2D，3D，4D情况下波浪荷载引起的管线周围海床响应.以e=2D的模型为例计算模型的网格划分，如图3所示.在管线周围进行局部网格加密处理以保证计算结果的精确性.每个数值模型共进行2个波浪周期时长的计算，计算时间步长为0.01 s，每0.1 s保存一次计算结果.此外，对埋管海床和自由海床的响应进行对比，波浪参数为H=2 m，T=8 s，L=70.93 m，h=12 m；海床土参数为Es=14 MPa，d=25 m，ns=0.4，Sr=0.98，νs=0.3，ρs=2 650 kg/m3，kz=0.001 m/s；管线参数为D=2 m，管线密度ρp=2 700 kg/m3，泊松比νp=0.32，弹性模量Ep=68 GPa，管壁厚度dp=0.2 m.

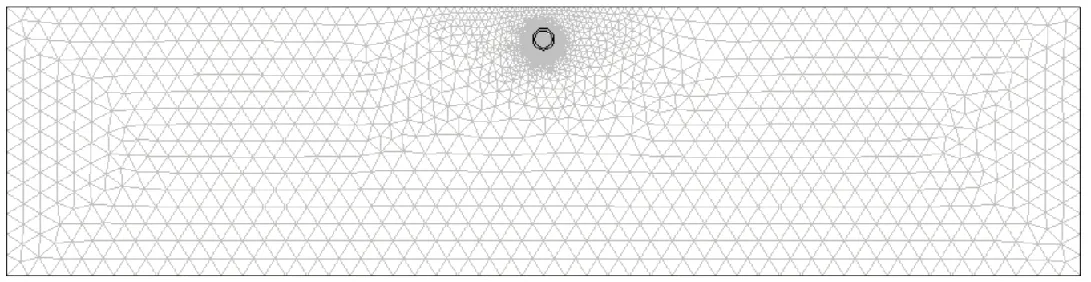
图3 数值模型网格划分Fig.3 Computational mesh of numerical model

2.1 埋管海床与自由海床响应对比

图4为在一个波浪周期内(t1=nT，t2=nT+T/4，t3=nT+T/2，t4=nT+3T/4)，埋管海床和自由海床的孔压和竖向有效应力沿海床土深度方向的变化趋势.其中，在t1时波峰到达管线上方.由图可知，管线对周围海床内孔压和竖向有效应力的分布影响十分明显，当波峰和波谷到达管线上方时，管线上方海床面分别达到最大正、负孔压，同时管线上、下侧分别达到最大正、负竖向有效应力；在t2和t4时，海床表面的孔压均为0，但是海床内部的孔压仍有残余.

图4 一个波浪周期内各海床土的孔压和竖向有效应力沿深度方向分布Fig.4 Distribution of pore pressure and vertical effective stress along seabed depth in one wave period

2.2 管线埋深对海床土响应的影响

图5为当波峰到达管线上方时，不同管线埋深情况下海床土的孔压和竖向有效应力沿海床土深度的变化.随着管线埋深的增加，其对管线上方海床土最大孔压的影响较小，但对管线下方海床土孔压的影响较大.相比于对孔压的影响，管线埋深变化对竖向有效应力的影响更明显.随着管线埋深的增加，管线上方海床土的竖向有效应力绝对值逐渐增加，而管线下方的竖向有效应力绝对值逐渐减小.

图6为一个波浪周期内，e=2D时管线周围的海床土的孔压和竖向有效应力分布.在一个波浪周期内，管线周围的最大正、负孔压均出现在管线角度θ=270° 附近，其中θ的定义如图7所示.此外，任一时刻的竖向有效应力在管线上、下方均呈反对称分布，最大竖向有效应力对称出现于管线上方θ=225°，315° 附近.

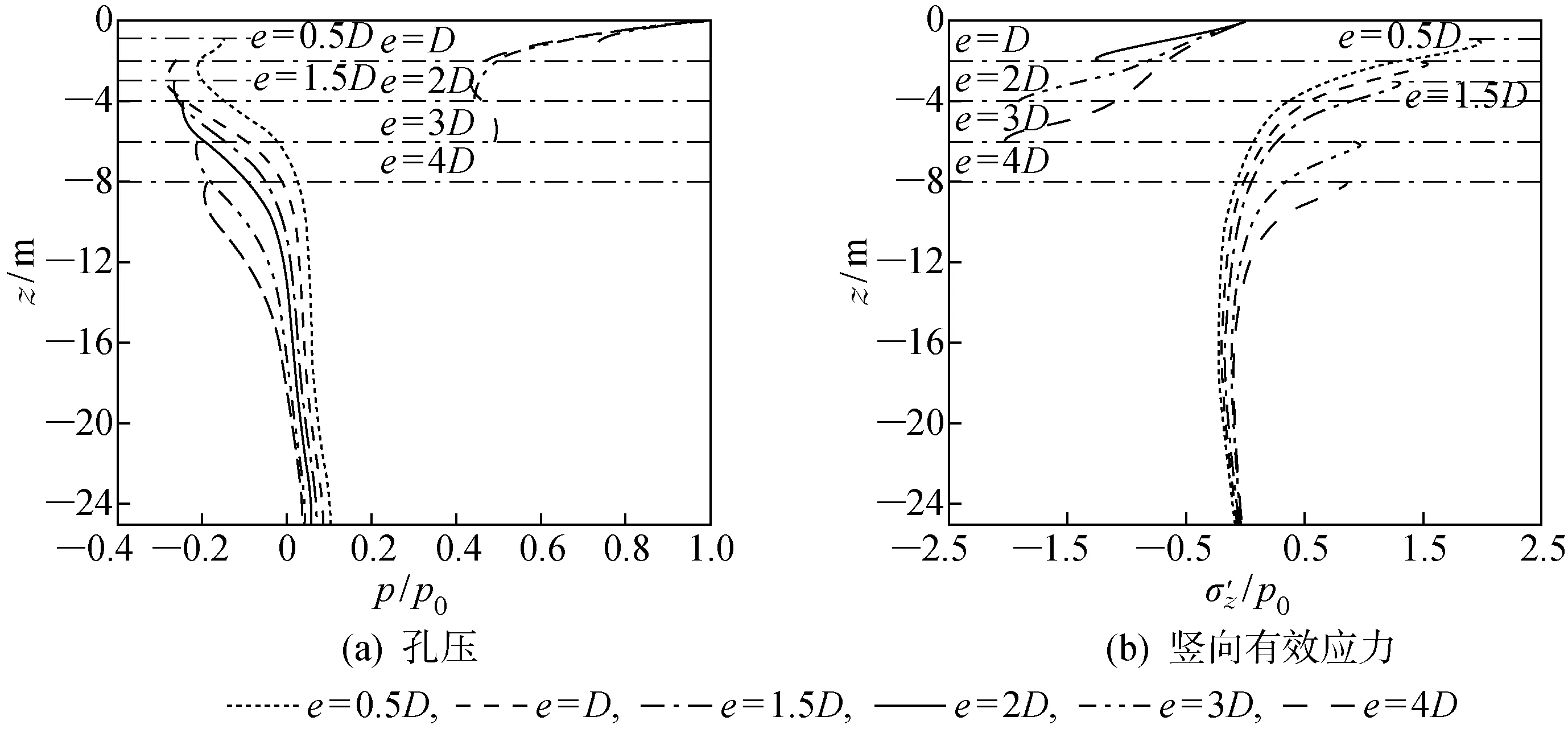
图5 不同管线埋深下的孔压和竖向有效应力沿深度方向分布Fig.5 Distribution of pore pressure and vertical effective stress along seabed depth at different pipeline buried depths

图6 一个波浪周期内的孔压和竖向有效应力分布Fig.6 Distribution of pore pressure and vertical effective stress in one wave period

图7 管线角度定义Fig.7 Definition of pipeline angle

图8为当波峰到达管线上方位置时，不同管线埋深的孔压和竖向有效应力分布.海床土的孔压随管线埋深的增加而逐渐减小，在e>2D时减小效果不明显.管线周围海床土的竖向有效正应力均出现在管线下方两侧，且竖向有效正应力随埋深的增加而减小.

图9为海床土的液化区域随管线埋深的变化情况.随着管线埋深从D增至2D，最大液化深度缓慢增加，但海床的液化区形状相似.当e=2D时，液化深度为6.42 m.当e=3D时，管线不处于液化区域，海床的液化区位于管线上方并形成凸起(见图9(b)).当e=4D时，管线上方未液化区的凸起变缓.因此，在当前波浪荷载和海床土条件下，当e>3D时，管线不再处于海床液化区范围内.

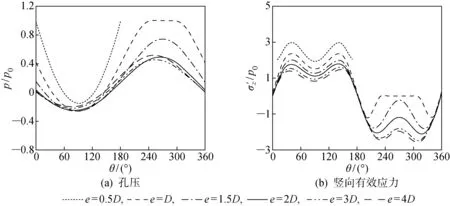
图8 不同管线埋深下管线周围的孔压和竖向有效应力分布Fig.8 Distribution of pore pressure and vertical effective stress aroud pipeline at different pipeline buried depths

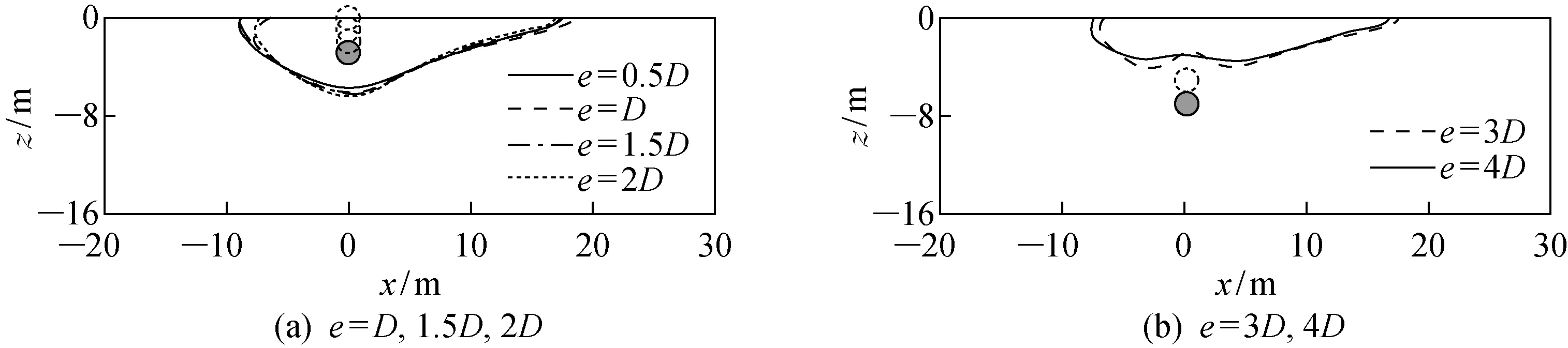
图9 不同管线埋深下海床土的液化区域Fig.9 Liquefaction depth of seabed at different pipeline buried depths

2.3 波浪与海床土参数分析

图10为在不同波高情况下，管线周围海床土孔压沿深度的变化.波高变化直接影响海床表面孔压的分布，因此海床表面最大孔压均随波高的增加而增大，而与管线埋深基本无关.不同管线埋深对管线上方海床土孔压的影响较小，而对管线下方海床土孔压的影响较大.

图11为在不同海床土渗透系数下，管线周围海床土孔压沿深度的变化.其中，kz=0.01，0.001，0.000 1 m/s分别对应粗砂、中砂和细沙海床的情况.随着管线埋深逐渐增加，渗透系数对管线下方孔压的影响略有减小，而对管线上方海床土孔压的影响逐渐增大.管线上方海床土孔压沿海床土深度方向减小的速率随渗透系数的减小而增大.但当kz=0.000 1 m/s时，在H=-1 m的位置出现了反弯点，孔压逐渐增大，这是由于管线的存在影响了孔压的分布，所以反弯点的位置随着管线埋深的增加而逐渐下移.

图10 不同波高下的孔压沿深度方向分布Fig.10 Distribution of pore pressure along seabed depth at different wave heights

图12为在不同海床土饱和度下，管线周围海床土孔压沿深度的变化， 考虑基本饱和和完全饱和砂质海床的差异.管线上方海床土孔压沿海床土深度方向的减小速率随饱和度的增加而减小，即饱和度越高海床土孔压的减小速率越小.同时，管线下方海床土孔压的绝对值随海床土饱和度的增加而增大.

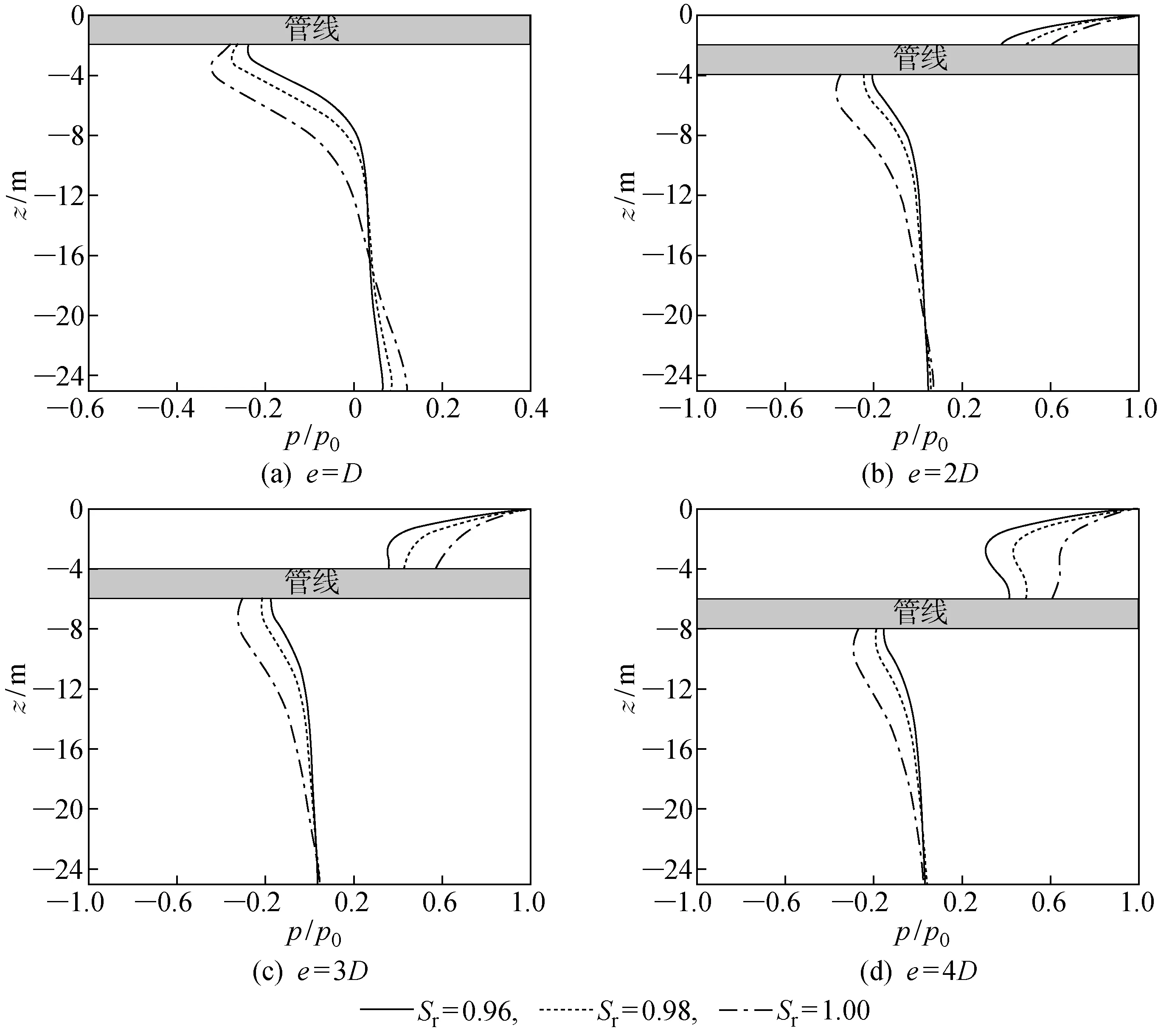
图12 不同海床土饱和度下的孔压沿深度方向分布Fig.12 Distribution of pore pressure along seabed depth at different seabed soil saturations

3 结论

(1) 管线的存在使得其周围海床土的竖向有效应力出现应力集中现象.在一个波浪周期内，管线周围的孔压和竖向有效应力发生周期性变化，管线周围的最大孔压出现在θ=270° 附近.

(2) 管线埋深对海床土的孔压和竖向有效应力影响明显.管线周围海床孔压随管线埋深的增加而逐渐减小，最大竖向有效正应力出现在管线下方两侧，且随着埋深的增加而逐渐减小.

(3) 随着管线埋深从0.5D增至2D，管线周围海床土液化区的形状相似，且最大液化深度缓慢增加.当e=3D,4D时，海床土的液化区发生明显变化，管线不再处于液化区域内.

(4) 在不同波高下，管线埋深对管线下方海床土的孔压影响更明显.随着管线埋深的增加，海床土渗透系数对管线下方孔压的影响略有减小，对管线上方孔压的影响逐渐增加.管线上方海床土孔压减小速率随饱和度的增加而减小，管线下方海床土孔压的绝对值随饱和度的增加而增大.