基于Newton法优化ARMA模型参数的船舶升沉运动预测研究

唐 刚，姚小强，胡 雄

(上海海事大学 物流工程学院，上海 201306)

船舶在海上作业时受到海浪的影响，会有明显的横摇、纵摇和升沉运动。目前，很多船舶己经具备动力定位系统，船舶的横摇、纵摇运动得到较好的控制，而升沉运动的补偿则需要通过波浪补偿装置来实现，但由于波浪补偿装置存在明显的时延问题，严重影响船舶运动的补偿精度和稳定性[1]。为了减小系统响应的时间滞后，通过对船舶的升沉运动进行预报，提前控制船舶的运动姿态，不仅能解决波浪补偿系统的时延问题还能提高船舶在海上作业的安全性及效率，在军事和民用领域具有重要价值。

船舶运动姿态预测方法主要分为频域方法和时域方法，频域方法主要有统计预报法和卷积法等[2-3]，但这些方法很难得到精确的响应核函数和波高测量函数，且运算速度较慢，因此频域方法在实际应用中逐渐消失。时域方法主要有艏前波法、卡尔曼滤波法和时间序列法等[4-7]，时域法通过船舶运动姿态的历史数据建模，预测未来较短时间内船舶的运动状态，预测精度较高且计算速度快，因此常用于工程实际中。

时间序列分析法对波浪补偿的时延具有较好的预测效果，且在线计算量小，实时性较好，同时对干扰和丢包等因素具有良好的鲁棒性。Peng等[8]使用自回归滑动平均(ARMA)模型对大型船舶姿态运动进行建模和预报，利用AIC准则确定ARMA模型的阶数，缩短了船舶运动预报的计算时间并解决了ARMA 模型阶数选择的在线估计问题。Wei等[9]基于ARMA模型预测舰载直升机平台的广义升沉运动(横摇、纵摇以及升沉方向的耦合运动)，使用阻尼递归最小二乘(DRLS)算法估计ARMA模型的参数，仿真结果表明ARMA模型可以较准确对舰载直升机平台的广义升沉位移进行多步预测。

当波浪补偿系统具有随机噪声时，ARMA模型的参数估计容易漂移并且不稳定。因此，引入Newton法[10]优化ARMA模型参数，将模型的残差平方和作为目标函数，通过反复迭代模型参数初值，使得模型的残差平方和为极小值，仿真结果表明使用Newton法优化ARMA模型参数可以提高船舶升沉运动的预测精度。

1 加速度信号的采集与处理

1.1 升沉运动加速度信号采集

船舶升沉运动加速度信号是基于惯性测量单元(IMU)采集所得，IMU由加速度传感器和陀螺仪组成，加速度传感器可以用于测量船舶横荡、纵荡以及升沉运动的加速度信号，陀螺仪可以用于测量船舶的横摇、纵摇以及艏摇的角速度信号。将其安装在船舶的船舶重心位置，设置采样频率为100 Hz，采集不同海况下船舶升沉运动的加速度信号。本文使用的仿真数据为船舶在二级海况、三级海况和四级海况[11]下航行的三组加速度信号{zt}，部分观测数据见表1。

表1 船舶运动姿态观测数据表(部分)Tab. 1 Ship motion attitude observation data table (partial)

1.2 卡尔曼滤波

采集信号时由于传感器自身和外界环境的影响，加速度信号中包含大量白噪声，因此需要设计滤波器对加速度信号进行降噪滤波处理。卡尔曼滤波器建模简单，数据解算速度快[12]，只需通过前一个估计值及观测数据估计当前的信号值，采用递推方式实时更新观测数据，就可以解算出新的卡尔曼滤波值，因此很适合用来处理船舶升沉运动加速度信号。

由于采集到的不同海况下升沉运动的加速度信号为离散信号，因此需要先建立离散卡尔曼滤波器[13-14]，其系统状态方程和测量方程如式(1)所示。

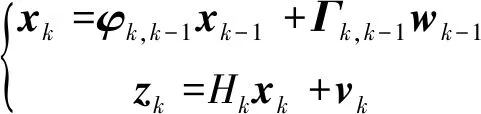
(1)

系统的最优预测误差协方差矩阵Pk,k-1和最优增益矩阵Kk计算如式(2)所示。

(2)

式中：φk,k-1为系统状态转移矩阵，xk-1为k-1时刻系统状态量；Γk,k-1为噪声系数矩阵，wk-1为系统噪声；zk为k时刻系统测量值，Hk为系统测量矩阵，vk为测量噪声；Qk-1,Rk分别为系统动态噪声wk-1和观测噪声vk的方差阵。

利用公式(1)和(2)可以计算出k时刻系统状态的最优滤波值，如式(3)所示。

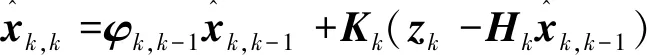
(3)

将二级海况、三级海况和四级海况下的三组升沉运动加速度信号输入到设计好的卡尔曼滤波器中，得到滤波后的加速度信号曲线，如图1、图2和图3所示。对比原始加速度信号和滤波后的加速度信号波形图可知，设计的卡尔曼滤波器能较好的去除白噪声，保留加速度信号的原有特征。

为了评估卡尔曼滤波器对升沉运动加速度信号的滤波效果，引入信噪比(SNR)以及相关系数(R)。其中，信噪比为信号中有效成分与噪声成分功率之比，是描述两种成分之间比例关系的参数；相关系数可以反映原始加速度信号和滤波后的加速度信号之间的相关程度，计算公式如下所示。

(4)

(5)

式中：xk为原始加速度信号，yk为滤波后的加速度信号。

表2 卡尔曼滤波器在不同海况下的SNR和R值Tab. 2 SNR and R values of Kalman filter under different sea states

图1 二级海况下加速度信号滤波前后对比Fig. 1 Comparison of the acceleration signal before and after filtering in the level-two sea state

图2 三级海况下加速度信号滤波前后对比Fig. 2 Comparison of the acceleration signal before and after filtering in the level-three sea state

图3 四级海况下加速度信号滤波前后对比Fig. 3 Comparison of the acceleration signal before and after filtering in the level-four sea state

表2总结了卡尔曼滤波器在不同海况下的信噪比SNR和相关系数R，可知三级海况下卡尔曼滤波器的信噪比最低，平均值为42.630 4，二级海况下最高，平均可达到66.990 8。此外，原始加速度信号和滤波后的加速度信号的相关系数均在0.9以上，说明加速度信号使用卡尔曼滤波器具有很好的滤波效果。

1.3 加速度二次积分

波浪补偿装置主要控制船舶升沉运动的位移信号，因此需要将加速度信号转换成位移信号。由于船舶升沉运动的加速度信号为低频信号，采用两次频域积分会导致低频信号误差较大，影响积分后的位移信号精度[15]，又因为加速度信号中包含一定的误差项，采用两次时域积分会产生较大的累积误差[16]。因此，使用时域-频域积分，既避免了时域积分中二次趋势项的产生，也降低了频域积分对低频信号精度造成的影响[17-18]。首先进行时域积分，离散加速度信号的时域积分方法主要有梯形积分和辛普森积分等，其中梯形公式由于计算简单、精度高而被广泛使用，其速度计算公式为

(6)

式中：v为积分后的速度值，a为加速度信号，fs为采样频率。

其次将得到的速度值v(i)进行傅里叶变换得到速度的频域值V(k)，然后在频域上积分，计算公式如式(7)、式(8)：

(7)

(8)

式中：S(r)为位移的频域值，Δf为频率分辨率。H(k)为频域值带通滤波器的带宽，如式(9)所示，fd为下限截止频率，fu为上限截止频率。

(9)

在频域积分中，上、下限截止频率会影响积分误差的大小, 其确定方法主要有两种：若加速度信号的频带已知，则将信号的频带上、下限频率作为频域积分的上限截止频率和下限截止频率；若加速度信号的频带未知，首先对加速度信号进行频谱分析，将功率谱密度曲线中显著低于其它频带的频率点作为频域积分的下限截止频率，显著高于其它频带的频率点作为频域积分的上限截止频率。

根据时域-频域积分法，在MATLAB软件中设计加速度二次积分模块，将滤波后的加速度信号积分为位移信号，图4、图5和图6分别为二级海况、三级海况和四级海况下船舶升沉运动加速度和位移波形图。由图可知，随着海况增大，升沉位移的幅值也越来越大，此外，低海况时船舶升沉位移曲线较平稳，高海况时变化较为剧烈。另外，采用频域积分将时域积分中产生的趋势项消除，使得积分后的位移曲线更加平滑。

图4 二级海况下加速度和位移波形Fig. 4 Acceleration and displacement wave forms in the level-two sea state

图5 三级海况下加速度和位移波形Fig. 5 Acceleration and displacement wave forms in the level-three sea state

图6 四级海况下加速度和位移波形Fig. 6 Acceleration and displacement wave forms in the level-four sea state

2 ARMA模型

ARMA模型的建立主要包括模型定阶、参数估计和参数优化等过程[19]。设{xt}(t=1, 2, ……,N)为加速度二次积分得到的船舶升沉运动位移数据，船舶运动姿态位移xt不仅与其前k步的位移xt-1,xt-2, ……,xt-k有关，而且还和前l步的各项位移扰动yt-1,yt-2, ……,yt-k有关(k,l=1, 2, ……)，ARMA模型的数学表达式如式(10)所示：

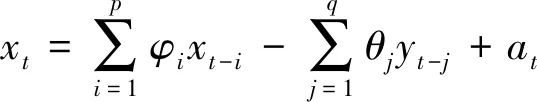
(10)

式中：p,q分别表示自回归部分和滑动平均部分的阶次；φi和θj分别为AR和MA部分的模型参数；at为测量误差，通常为白噪声序列。

2.1 ARMA模型定阶

模型定阶是为了寻找ARMA模型的最佳阶数，本文通过采用AIC准则和BIC准则共同定阶，以便在模型预测精度与模型计算复杂度之间寻找平衡。其中，AIC准则由日本学者Akaike H[20]于1974年首次提出，是一种衡量统计模型拟合优良性的标准。BIC准则由Schwarz[21]于1978年提出，通过加入模型复杂度惩罚因子来避免出现过拟合问题。

设{xt,t=1, 2, ……,N}为船舶升沉运动的位移数据，利用模型参数估计方法可以获得在不同阶数下的ARMA(p,q)模型，并计算出相应的AIC值和BIC值，如公式(11)所示：

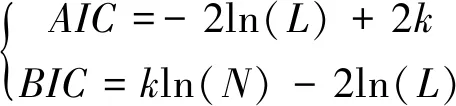
(11)

式中：k为模型参数个数，N为样本数量；L为似然函数，计算公式如式(12)所示。惩罚项k·lnN在维数过大且训练样本数据较少时，可以有效避免维度灾难问题。当AIC最小且BIC最小时，p和q为ARMA模型最佳的模型阶数。

(12)

2.2 ARMA模型参数估计

长自回归模型计算残差法可以将ARMA 模型参数的非线性估计问题转变为AR模型参数的线性估计问题，极大简化计算过程，提高ARMA模型的预测效率[22-23]。本文采用该方法估计ARMA模型中的参数φi和θj，其基本原理为：同一升沉运动位移时序数据{xt}拟合成的AR(n) 模型和ARMA(p，q) 模型可以看成等价系统，两种模型在同一时刻的残差值at应相等。因此，可以将位移时序{xt}拟合出的AR(n) 模型的残差at作为ARMA(p,q) 模型的at，再通过最小二乘法求解模型参数，其计算步骤如下所示。

首先将船舶升沉运动位移时序{xt}拟合出合适的AR(n)(n≥p+q)模型，得到模型参数φi(i=1, 2, ……,n)，然后计算残差序列at。

(13)

通过AR(n)模型可以得到从t=n+1至t=N的残差序列{at}，将{at}代入ARMA(p，q)模型中，如矩阵方程(14)所示。

Y=Xβ+A

(14)

式中：Y为船舶升沉位移预测值矩阵；X为升沉位移测量值矩阵；β为ARMA模型参数矩阵；A为白噪声序列；如公式(15)～(18)所示。

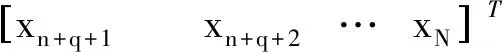
(15)

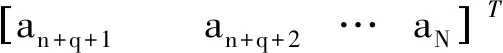
(16)

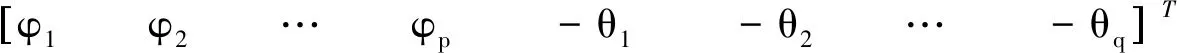
(17)

(18)

由于矩阵X中的参数均已知，可以使用最小二乘法估计模型参数β，见式(19)。

β=(XTX)-1XTY

(19)

长自回归模型计算残差法的参数估计流程如图7所示。

图7 长自回归模型计算残差法流程Fig. 7 Flow chart of long auto-regressive model calculation residual method

3 Newton-ARMA模型

3.1 ARMA模型参数优化目标函数

前述ARMA模型可以表示为公式(20)的形式：

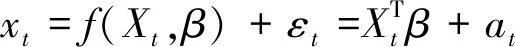
(20)

式中：Xt如公式(15)所示，由不同时刻船舶升沉运动加速度信号组成；β如公式(14)所示；at为模型的残差。

为了选择合适的模型参数β，通过建立目标函数S(β)，如公式(21)所示，将参数β的估计问题转化为对S(β)的寻优问题，即保证模型的残差平方和S(β)为极小，本文利用Newton法求解模型参数β。

(21)

3.2 Newton法的迭代原理

首先在β(0)处对ARMA模型中的f(Xt,β)进行Taylor展开，并去掉二阶以上的高阶项，然后进行一系列线性最小二乘估计，直到迭代收敛到指定的范围[10, 24]。将参数初值β(0)代入模型中得到残差值，如公式(22)所示。

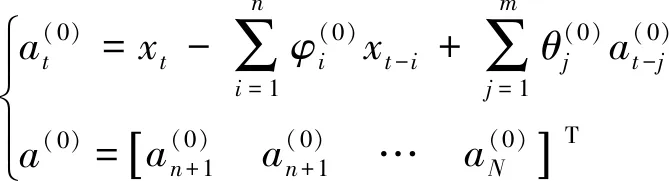
(22)

(23)

模型参数估计β与其初值β(0)之差可以通过公式(24)求得。

h(0)=[v(0)Tv(0)]-1v(0)Ta(0)

(24)

3.3 Newton法参数寻优过程

图8 Newton法参数寻优流程Fig. 8 Flow chart of parameter optimization by Newton method

步骤2：设l为迭代循环变量，第一次迭代前设置l=0；

步骤4：按照公式(24)估计出h(l)；

步骤5：判断h(l)是否小于预设的精度界限δ，即迭代结果是否收敛，如果h(l)<δ，则ARMA模型参数的估计值为β=β(l)+h(l)，如果h(l)≥δ，则进行下一步迭代运算；

步骤6：将β(l+1)=β(l)+h(l)作为下一次迭代计算的初值，令l=l+1转入步骤3中继续迭代，直到h(l)<δ迭代结束。Newton法参数寻优过程的流程如图8所示。

4 仿真结果分析

仿真数据为加速度二次积分模块得到的船舶升沉运动位移数据，建立Newton-ARMA模型首先进行模型定阶，根据上述步骤1，令ARMA模型中自回归部分的阶数p从1到10，滑动平均部分的阶数q从1到10，分别求出各阶数的AIC和BIC值，找出不同阶数下AIC和BIC的最小值，即为模型的最佳阶数，如表3所示。

表3 不同阶数下的AIC和BIC值Tab. 3 AIC and BIC values at different orders

由表3可知，二级海况下Newton-ARMA模型的最佳阶数为p=8，q=3，三级海况下Newton-ARMA模型的最佳阶数为p=7，q=3，四级海况下Newton-ARMA模型的最佳阶数为p=6，q=3。根据最佳阶数建立ARMA模型，利用长自回归模型计算残差法得到模型参数初值β(0)，并利用Newton法对β(0)进行迭代寻优，设置精度界限δ=10-5，运算完成后得到不同海况下升沉运动1、升沉运动2和升沉运动3的Newton-ARMA模型参数估计值β，如表4所示。

表4 不同海况下升沉运动的Newton-ARMA模型参数Tab. 4 Newton-ARMA model parameters for heave motion in different sea states

基于得到的三种海况下船舶升沉运动的Newton-ARMA模型，分别进行1 s到10 s的预测，预测结果如图9、图10和图11所示。图中实线(每段100 s，共9段)表示测量的船舶升沉运动位移信号曲线；实线(每段90 s，共9段)表示使用Newton-ARMA模型拟合出的船舶升沉运动位移曲线；虚线(每段10 s，共9段)表示使用Newton-ARMA模型预测10 s内船舶升沉运动位移曲线；点画线(每段90 s，共9段)表示只使用ARMA模型拟合出的船舶升沉运动位移曲线；点线(每段10 s，共9段)表示只使用ARMA模型预测10 s内船舶升沉运动位移曲线。由图可知，Newton-ARMA模型拟合出的船舶升沉运动位移曲线更贴近于测量数据的升沉位移曲线，说明使用Newton法优化ARMA模型参数使得预测模型可以更加真实地反映船舶实际的升沉运动状态，通过对比Newton-ARMA模型和ARMA模型预测10 s内船舶升沉运动位移的曲线，能够很好地证明该结论。

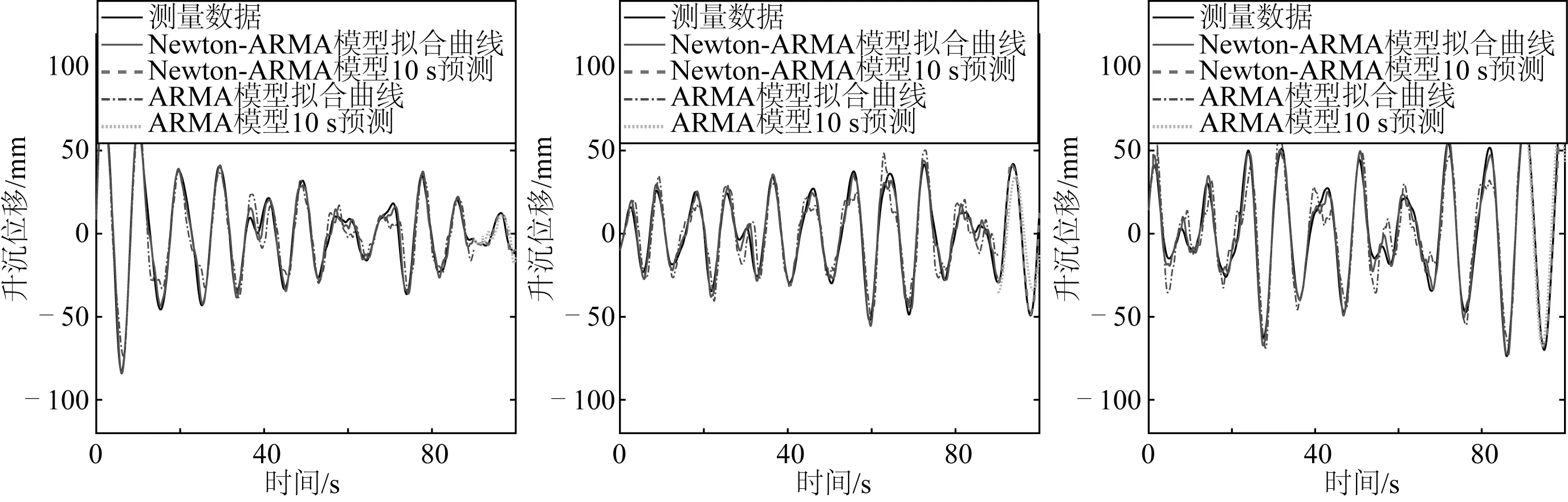
图9 二级海况下船舶升沉运动预报曲线Fig. 9 Ship heave motion prediction curve in level-two sea state

图10 三级海况下船舶升沉运动预报曲线Fig. 10 Ship heave motion prediction curve in level-three sea state

图11 四级海况下船舶升沉运动预报曲线Fig. 11 Ship heave motion prediction curve in level-four sea state

根据建立的不同预测模型，可以分别求解出不同时长时预测值与测量值的均方根误差RMSE，如图12所示。由图可知，随着预测时间的增大均方误差不断增大，预测精度逐渐减小。以Newton-ARMA模型为例，在预测二级海况的升沉运动1中，当预测时间从1 s增加到10 s时，均方误差值从0.004 3 m增加到0.032 8 m。此外，使用ARMA模型对二级海况、三级海况和四级海况升沉运动的平均预测精度分别为85.31%、82.46%以及80.21%，而使用Newton-ARMA模型的平均预测精度分别可达89.43%、88.53%以及87.78%，由此可知采用Newton法优化ARMA模型参数可以显著提高船舶升沉运动的预测精度。

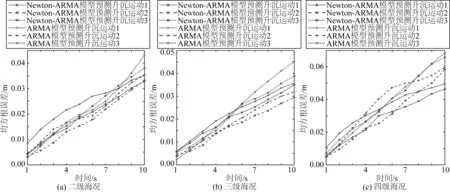
图12 船舶运动预报均方根误差Fig. 12 Ship motion prediction root mean square error

5 结 语

使用Newton法对ARMA模型参数进行优化，得到不同海况下船舶升沉运动的Newton-ARMA预测模型，仿真结果表明，Newton-ARMA模型对船舶升沉运动的预测时间可达10 s以上，有效地减小了波浪补偿装置控制系统的时延，且预测精度得到显著提升，最高可达89.43%，由此表明Newton-ARMA模型对船舶升沉运动具有较好的预测效果。此外，建立Newton-ARMA模型首先采用AIC准则和BIC准则共同确定模型的阶数，可以避免出现过拟合现象导致模型复杂的问题；利用长自回归模型计算残差法计算模型参数初值，可以将非线性估计问题转化为线性估计问题，简化了计算过程，使得寻优迭代速度更快。