黏性土底床中桩基底部吸力试验研究

于 徽，王闻恺

(交通运输部水运科学研究院，北京 100088)

随着海洋开发事业的日益发展，海洋工程结构物的应用也逐渐增多，这些海工设施的锚定需要利用不同种类的海底锚固装置，如锚、桩等[1-2]。如海洋平台、海上风机、海洋养殖网箱等均需要利用海洋工程锚(板锚、吸力锚等)或桩基基础来使其位置保持固定[3-5]。当海底结构物受海上风、流影响发生上拔动作时，锚固设施的底面与土体之间产生一定程度的吸力。吸力是由锚固设施形状、底床土体性质和土中孔隙水三者之间复杂的相互作用形成，表现为一种类似“真空吸力”的拉力[6]。由此可见，锚固设施底部吸力对上拔过程产生了阻碍作用，增加了锚固设施的抗拔力。因此，开展有关锚固设施底面吸力的研究具有重要的现实意义。

目前，国内外学者对海底设施底面吸力开展了研究，并取得了一定成果。20世纪60年代，美国海军土木工程实验室[7]在加州港测定了最大浮重度为90 kN，底面形状不同的海底结构物的吸力。研究发现，吸力是海底泥沙与水之间复杂相互作用所产生的结果。冯国栋等[8]就海泥对海洋工程结构物底面的吸力进行了试验观测，发现该吸力并不是简单地反映工程材料与泥土间的黏着力，而主要是底面下存在的真空吸力，涉及泥沙的流变、固结和触变性质。Das等[9]也测定了软黏土与硬黏土中不同底面形状的板锚在不同荷载条件下的底面吸力，但他们的分析并未考虑拉拔速度、埋置深度等对吸力的影响。Datta和Kumar[10]在不排水条件下测量了圆柱形锚在不同埋深条件下的吸力，发现吸力随着埋深的增大而增大，直到埋深与直径的比值为8时达到极限；但他们的拔锚速度很慢，且未能提出可靠的吸力计算公式。Kassim和Niroumand[11]通过试验提出了计算卧式平板锚吸力的公式，但该公式的计算精度一般。王子宾[6]探讨了桩靴上拔时底部吸力的成因和作用方式，但并未总结出实质性的结论。综上所述，对锚固设施底部吸力的变化特性仍需要进一步深入研究。

为研究锚固设施底部吸力特性，设计了光滑闭口短桩在黏性土底床上拔试验方案，利用孔隙水压力传感器、超声波多普勒流速仪(UDV)、拉力传感器以及步进电机等试验设备测量桩基模型在垂向上拔过程中底部吸力、腔体深度和拉拔力的变化并分析其成因，还分析了桩体上拔过程中吸力的变化过程及桩体的埋置深度和上拔速度对吸力大小的影响，最后通过对试验数据的回归分析，得到了计算黏性土底床中桩基/基础在上拔过程中所受最大吸力的经验公式。试验过程及结论可为其它锚固设施的抗拔力研究起到借鉴作用。

1 理论分析

如图1所示，以圆柱形桩为例，桩基在黏性底床垂直上拔过程中，所受到的力主要有土体对桩基侧面提供的侧摩阻力、桩基浮重力和桩基底部所受的吸力，可以表示为：

FPU=Wa+FAD+FSU

(1)

式中：FPU为拉拔力，Wa为桩基浮重力，FAD为侧摩阻力，FSU为吸力。

根据Terzaghi和Peck[12]的常规土力学公式，侧摩阻力可以表示为：

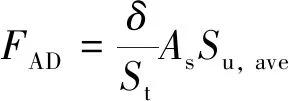
(2)

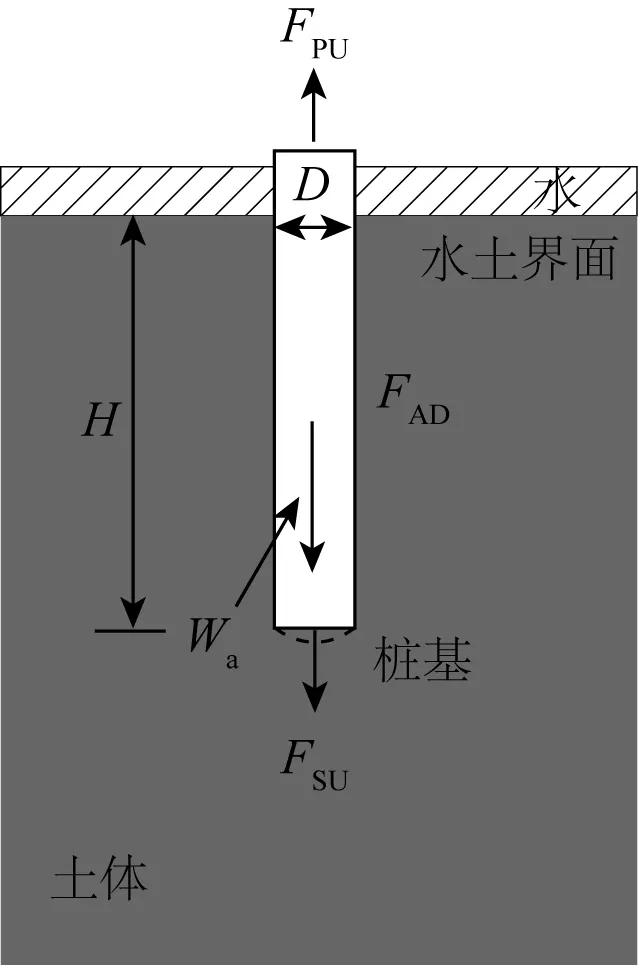
图1 桩基在垂直拔出时受力情况Fig. 1 Forces on pile foundation during pullout

式中：δ为黏附力系数，St为土体的灵敏度，As为桩基没入土体的侧面积，Su,ave为土体平均不排水抗剪强度。非光滑物体在黏性土中以较低速度运动时的黏附力系数(δ)可以近似为1[13-14]。该理论公式已被其他学者广泛使用，如Raie等[15]，O’Loughlin等[16]。Blake和O’Loughlin[13]利用该理论公式研究物体在黏性土底床中拔出时的受力问题，充分证明了该理论公式的科学性与合理性[17]。

Das[9]等通过试验，提出了计算板锚下方吸力的经验公式：

(3)

式中：AF为锚底面积，Su为土体不排水抗剪强度，H为埋深，D为桩基底面直径。

从公式(3)可以看出，板锚底部吸力与锚体底部面积AF、土体不排水抗剪强度Su及埋深比(锚体埋置深度与锚直径的比值)H/D有关。另外，相同土体中锚体以不同速度拔出时底部吸力会因土体变形速率或孔隙水的流动速度不同而产生较大差别，而土体变形速率和孔隙水流动速率与锚体上拔速度相关[10]，因此，锚体(或桩基)下方吸力可以用更加概括的函数形式表达：

(4)

通过式(1)、(2)、(4)可以得到桩基的最大垂向抗拔力计算表达式：

(5)

2 试验研究

2.1 试验用土

试验用土样取自上海金山港。试验前将土样过滤，筛除内部杂质，进行充分搅拌，对土体的含水率ω、中值粒径d50、不排水抗剪强度Su、灵敏度St、密度ρ、渗透系数k、液限ωL和塑限ωP等参数进行测量记录。测量所得土体具体参数如表1所示。

表1 试验用土相关土力学参数Tab. 1 Parameters of testing soil

表2 十字板剪切仪测量数据Tab. 2 Measurement data of vane shear tester

图2 利用SZB-1.0型十字板剪切仪测量所得不排水抗剪强度剖面Fig. 2 Undrained shear strength profile measured by SZB-1.0

2.2 试验布置

试验选用一个内径35 cm、高60 cm的圆柱形不锈钢桶，桶内盛有55 cm深的试验用土。桩基模型长度L为26 cm，直径D为6 cm，质量m为1.26 kg。桩基模型底面设计3个孔，分别安装超声波多普勒流速仪(UDV)探头，孔隙水压力传感器和通气孔(桩基模型及底部布置情况如图3所示)。其中，超声波多普勒流速仪用于测量上拔过程中桩基底部腔体水深；孔隙水压力传感器用于测量腔体内压力值，进而计算吸力；通气孔安装可拆卸式密封螺栓，用来进行对比试验。传感器通过信号线与电脑连接，采集频率4 Hz。

如图4所示，在通气孔封闭(安装密封螺栓)的情况下，桩基模型在土中上拔时底部将产生吸力；通气孔打开时(拆除密封螺栓)，桩基模型底部将与外界大气连通，下方不产生吸力。通过对比试验，可获得桩基底部吸力值。

试验具体布置如图5所示，使用直径1.2 mm的钢丝线连接桩基模型，并通过定滑轮连接到拉力传感器，最后连接至步进电机；为方便试验操作，拉力传感器与电脑相连，拉力采集软件以4 Hz的频率采集拉力，并绘制拉力曲线图。步进电机转速通过调速器调节，控制上拔速度。

图3 桩基模型Fig. 3 Photos of the model pile foundation

图4 桩基模型密封与通气时底部受力Fig. 4 Forces on model pile foundation when bottom sealed and vented

图5 试验布置示意Fig. 5 Schematic of the experiment setup

2.3 试验步骤

试验主要操作步骤如下：

1)将事先制备完成的试验用土置于不锈钢桶中(土体上方水厚度约1 cm)，用搅拌器将土体搅拌均匀。

2)将桩基模型垂直缓慢匀速地插入土体中至指定深度(插入速度1 cm/s)，插入过程中控制好速度和方向，尽量避免对周围土体产生扰动，随后将土体静置10 min。

3)测量试验桶中土体的不排水抗剪强度Su和灵敏度St。

4)打开电脑，开启步进电机和调速器电源，调整好步进电机速度，开始拉拔桩基；同时开启UDV、孔隙水压力传感器、拉力传感器的采集软件，记录数据，直到桩基完全拉出土体。在桩基拔出过程中，UDV和孔隙水压力传感器分别记录了桩底部腔体水深及压力变化，拉力传感器记录拉拔过程中拉力的变化。

5)通过步骤1)的方法搅拌土体，使试验用土恢复，重复上述试验。

本研究共进行了30次拉拔试验。其中，对于同一埋深和相同土体性质条件下进行了底部密封和通气两种试验。拉拔速度分别为1、3、5、7和9 mm/s，圆柱桩埋置深度(H)分别为12、18和24 cm。表3列出了试验变量。图6为桩体埋设及拔出的两个不同状态。

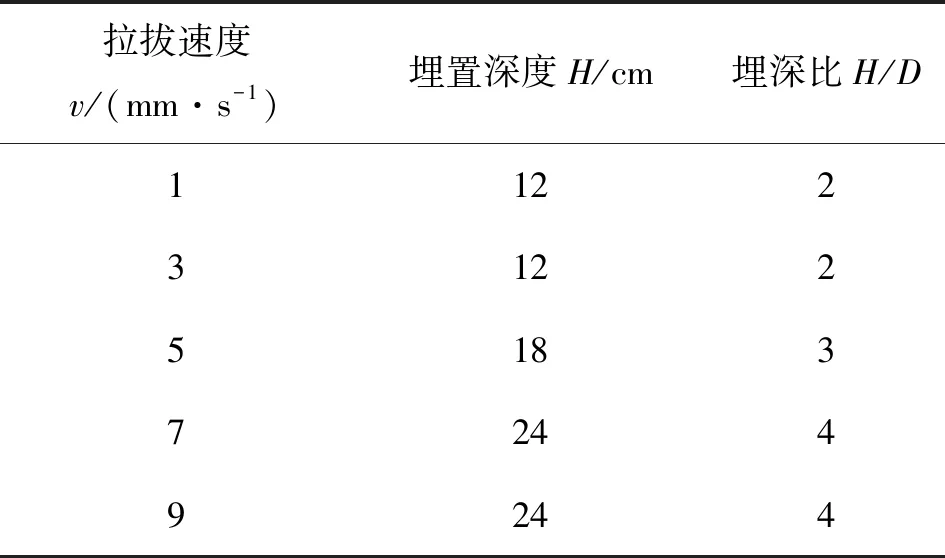
表3 试验变量Tab. 3 Test variables

图6 桩基模型埋设及拔出状态Fig. 6 The embedment and pullout states of model pile foundation

3 结果与分析

3.1 拉拔过程中桩基底部腔体变化特性

桩基在黏性土底床中上拔时，其下方土体由于具有一定结构强度(黏性及抗剪强度决定)，无法立即回填满由桩体上拔所腾出的空间，因此，其底部会产生一个含孔隙水的腔体。为观察这个腔体的形态变化，试验利用UDV探头来探测桩基下方腔体水深。图7为桩基在埋深24 cm和上拔速度1 mm/s情况下UDV探头采集的声波曲线。UDV探头在介质中发射超声波，当超声波遇水会继续传播，遇到障碍物后会发生反射，因此，该曲线的第一个波峰即为UDV探头下方腔体内水深。从图中可以看出，在15、16、17和18 s四个时刻探头下水的深度分别为1.956、2.046、2.218和2.406 mm。

根据试验数据，桩基下方水深的变化始终小于桩体的上拔速度(1 mm/s)，这说明桩基下方土体随着桩基上移发生了坍塌变形，不断回填桩基下方空间，使腔体大小保持相对稳定。

图7 桩基在24 cm埋深UDV声波曲线Fig. 7 Echo curve of UDV sound wave at embedment depth 24 cm

3.2 桩底部密封和通气条件下的压力特征

为了确定桩基底部吸力值的大小，分别进行了底部密封(底部腔体不与大气连通)与通气(底部腔体与大气连通)两种条件下的上拔试验。桩基埋入土体以后底部会受一定的静水压力，即孔隙水压强，其大小与埋置深度成正比。在埋深12 cm和上拔速度9 mm/s工况下，底部密封和通气两种不同条件下底部压力随拉拔时间的变化曲线如图8所示，桩体底部密封时，其下方压力值从3.644 kPa持续快速下降到-6.572 kPa，然后继续波动式缓慢下降，直到最小值-7.608 kPa；在桩体底部与土体分离瞬间，压力值立刻回升为标准大气压(以0为标准大气压)。在桩体下端与土体分离的时刻，会听见“砰”的进气声。而当底部开孔通气情况下，桩体下方压力值从1.612 kPa逐渐降低到标准大气压值，未出现小于标准大气压的情况。对于其它拉拔试验，底部压力变化均具有类似的特征。另外，在桩体插入过程中，孔隙水压力传感器数值逐渐增大，直至安装停止。通过桩体埋置深度计算该深度下的孔隙水压力(P=ρgh=1.2 kPa<3.6 kPa)可知，上拔初始时刻孔隙水压力大于该深度下的静水压力，说明在桩基插入试验的不排水土体过程中，对土体发生挤压扰动，产生了超静孔隙水压力。

利用以上试验可以得到桩体底部密封和通气条件下的最大拉力值，二者相减可以得出桩体底部最大吸力值为16.78 N (埋深12 cm和上拔速度9 mm/s工况)，而通过该工况下桩底最大负压计算得出的吸力值为21.5 N (FSU=P×πr2=7 608×3.14×0.032=21.5 N)，大于通过拉力值计算所得到的吸力值(其它试验工况该规律相同)，这是由于上拔过程中桩体受侧摩阻力等的影响，底部负压所产生的吸力最大值与拉力最大值不在同一时间点。

通过图9可以更加直观地发现，在底部密封条件下，由于负压所产生的吸力作用，桩基坑已经完全被土体回填满，且部分表层土发生隆起；在底部通气条件下，坑的轮廓基本保持桩基形状，只有较少侧壁摩擦和坍塌破坏。

图8 密封和通气条件下圆柱桩底部压力随拉拔时间变化Fig. 8 Pressure beneath the cylindrical pile against the pullout time in sealed and vented cases

图9 密封底和通气底条件下桩基坑变形情况Fig. 9 Deformation of pile foundation cavity under sealed and vented bottom conditions

3.3 拉拔过程中桩基底部压力的特性与影响因素

3.3.1 垂直拉拔过程中桩基受力变化特征

图10 桩底压力、拉拔力、腔体深度与时间关系Fig. 10 Bottom pressure, pullout force and cavity depth variations against pullout time

拉拔过程中桩基下方腔体深度、压力、拉拔力及吸力与拉拔力比值等参数随拉拔时间的变化如图10所示(桩体埋深12 cm，上拔速度5 mm/s工况)。在拉拔力FPU由零逐渐上升至最大值这段时间内(1～9 s期间)，压力由原来的正值减小变为负值，但并没有达到最大负压值(13 s时刻)，在拉拔力FPU达到最大值时桩体底部已经产生负压，且此时负压所产生的吸力占拉拔力约45%。在这段时间内，拉拔力主要由桩体底部所受压力P、桩体浮重力Wa和桩体侧摩阻力FAD组成。随后(第9～13 s间)，桩体底部负压绝对值继续上升至最大值，占总拉拔力的65%，而拉拔力则稳定在一定范围内(约3.6 kg)。随着桩体的继续拔出，侧摩阻力继续减小，可以推断，拉拔力主要由底部负压吸力和浮重力Wa组成。另外，由图10也可以看出，桩体底部负压出现的两次谷值(第13 s和第24 s)与腔体深度的两个峰值出现的时刻较为一致，这说明桩体底部的负压大小与腔体的水深大小成正相关。在桩体底部与土体分离的时刻，拉拔力FPU降为桩体自重，下方的腔体内负压消失，压力值恢复为标准大气压。

3.3.2 拉拔速度对压力的影响

试验中，分别采用1、3、5、7和9 mm/s五种不同拉拔速度对相同埋深及土质条件下的桩进行了匀速拔出试验。图11反映桩体在埋深12 cm时的五种不同上拔速度条件下桩体底部压力随时间的变化情况。通过分析可知，在相同埋深条件下，桩体底部压力绝对值的最大值随上拔速度增大而增大。即上拔速度越快，负压越大。随着上拔速度的增大，压力绝对值的增加值逐渐减小，说明上拔速度增大到一定值以后，对底部压力的影响不再明显。

此外，从图11中压力的变化趋势可以发现，桩体下方压力随着桩体上拔从初始的正压力值迅速降低到一个负压极值，随后波动变化并保持在一个相对稳定的负压范围；当桩体将要拔出底床时，压力突然升高至标准大气压。结合UDV传感器测量结果和图11不同拉拔速度的负压曲线的变化趋势特征分析可知：在开始上拔后，桩体底部形成了一个孔隙水腔体，腔体内压力值快速降低并达到最大负压值，此时腔体达到临界状态，即腔体边壁土体所受的负压所产生的吸力达到其屈服应力。此时，腔体边壁土体会发生破坏变形、垮塌，填充腔体，表现为负压值出现了一定程度的减小。随后，土体随桩基上拔不断回填，腔体负压值、形状与土体回填速度保持动态平衡。当桩基将要出土时，由于部分表层土被带起(图9所示)，形成“密封圈”，因此负压值再次增大到第二次极值，随后桩体与土体彻底脱离，压力瞬间恢复至大气压。

3.3.3 埋深比对压力的影响

图12反映了桩体在埋深比为2、3、4和拔出速度1 mm/s条件下底部压力随时间的变化情况，图中三条直线为桩体底部压力曲线对应同一时刻桩体在土体中的底部所受静水压力，由于是均匀土体，所以其静压力随深度成正比关系。桩体底部所受静水压力与该时刻底部压力的差值，即为该时刻桩体所受压力的大小。通过数据分析可得，桩体在上述埋深情况下的最大负压值分别为6.15、8.29和8.57 kPa。由此可知，桩体所受负压随桩体埋置深度的增加而增大。研究中其它试验结果也符合这一趋势。

试验用土在制备及搅拌恢复过程中上方始终保持一定厚度的水，可减少空气大量进入试验用土，避免形成孤立气泡，造成压力测量结果出现较大误差。非饱和土的土力学特性相对于饱和土要更为复杂，土体饱和度对桩体下方吸力影响将在后续试验中开展进一步研究。

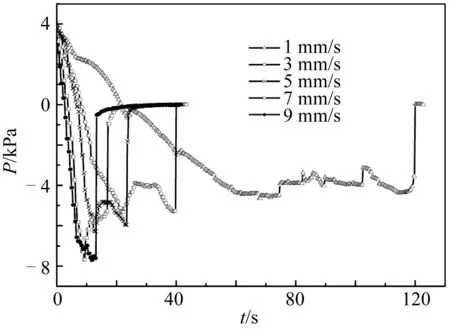
图11 不同上拔速度时桩体底部压力随拉拔时间变化Fig. 11 Suction force variations against pullout time at different pullout speeds

图12 不同埋深比情况下桩体底部压力随拉拔时间变化Fig. 12 Pressure variations beneath the cylindrical pile against pullout time at different embedment ratios

3.4 桩基底部最大吸力的经验公式

利用Das[9]的公式(3)对本次试验情况进行计算，将吸力计算值列于表4，发现其计算值与实测值差别较大。通过观察Datta和Kumar[10]对圆柱形锚的吸力与埋深比关系(见图13)，并对本次试验数据进行拟合分析，发现吸力与埋深比呈现指数关系。通过因次分析可得，桩基底部吸力可以表达为：

利用表4的实测数据进行多元回归分析可以得到

(6)

式中：回归结果的方差R2=0.94，说明公式(5)具有良好的回归精度。

通过式(1)、(2)、(6)可进一步得到桩基最大垂向抗拔力计算表达式

(7)

利用式(6)计算本次试验结果，得到吸力计算值与试验值的关系如图14所示，计算值基本在±20%的误差范围内，符合性较好。同时，利用式(6)验证Datta和Kumar[10]的试验结果(见表5)，可以发现约78%的计算值与试验值误差在±20%范围内，进一步验证了公式(6)用于计算桩体底部吸力的准确性。

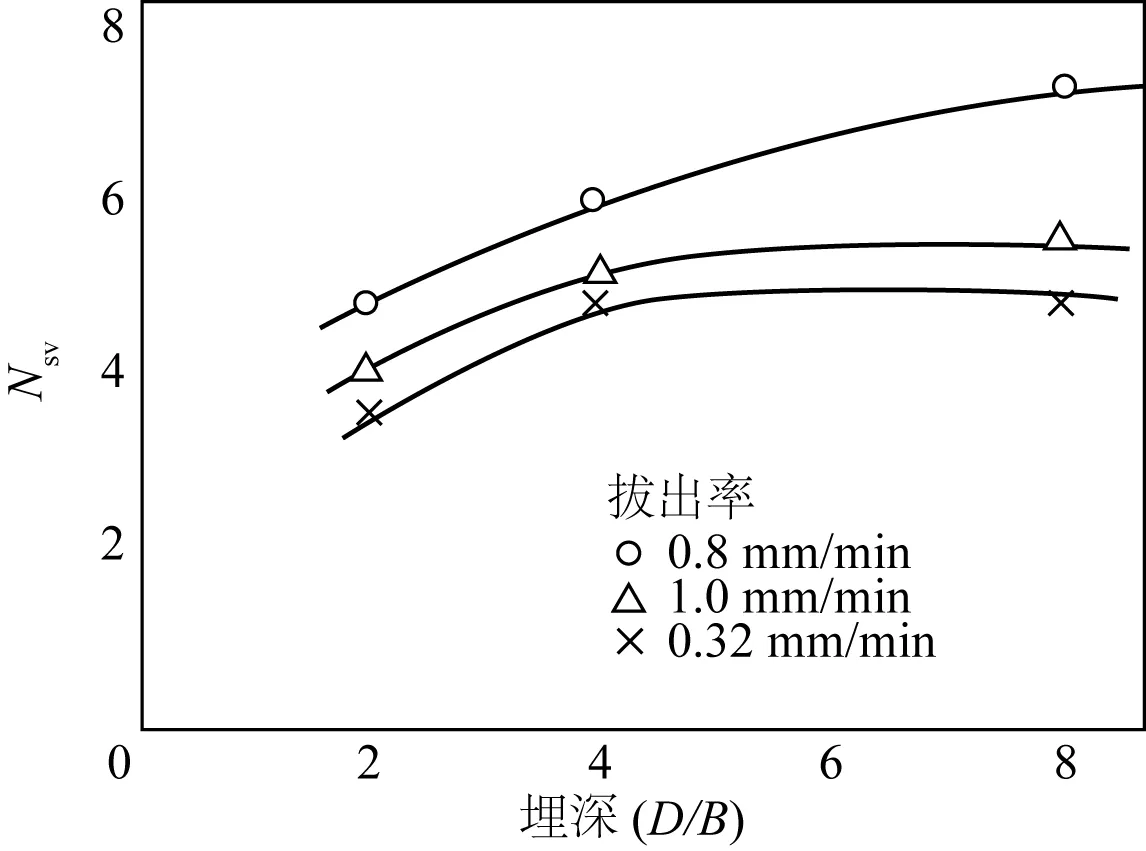
图13 Datta and Kumar吸力系数与埋深比关系[10]Fig. 13 Datta and Kumar variation of suction breakout factor with embedment depth[10]

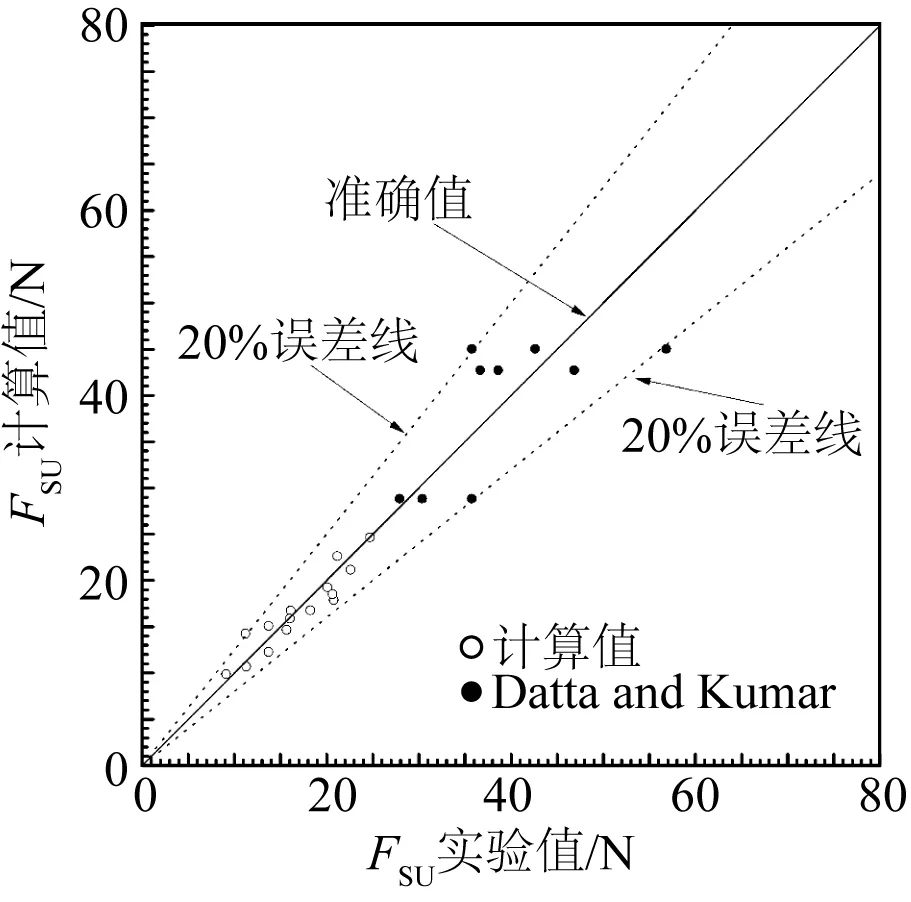
图14 垂向拉拔吸力计算值与理论值比较Fig. 14 Comparison between the experimental and calculated suction forces during vertical pullout

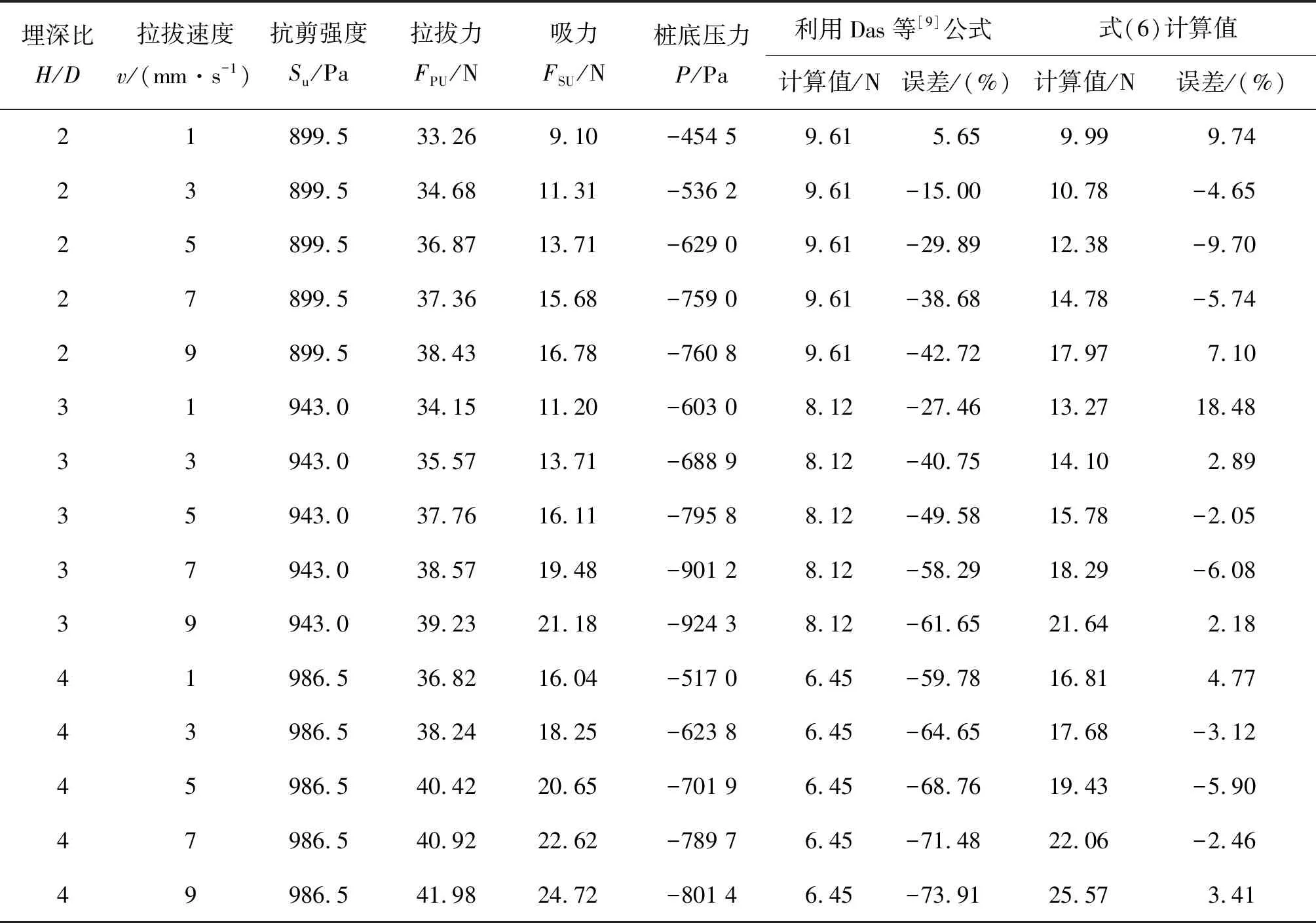
表4 试验结果分析Tab. 4 Analysis of the experimental results

注：拉拔力数据为桩底密封的最大拉力值；吸力为桩底密封和通气所测量的最大拉力值之差。

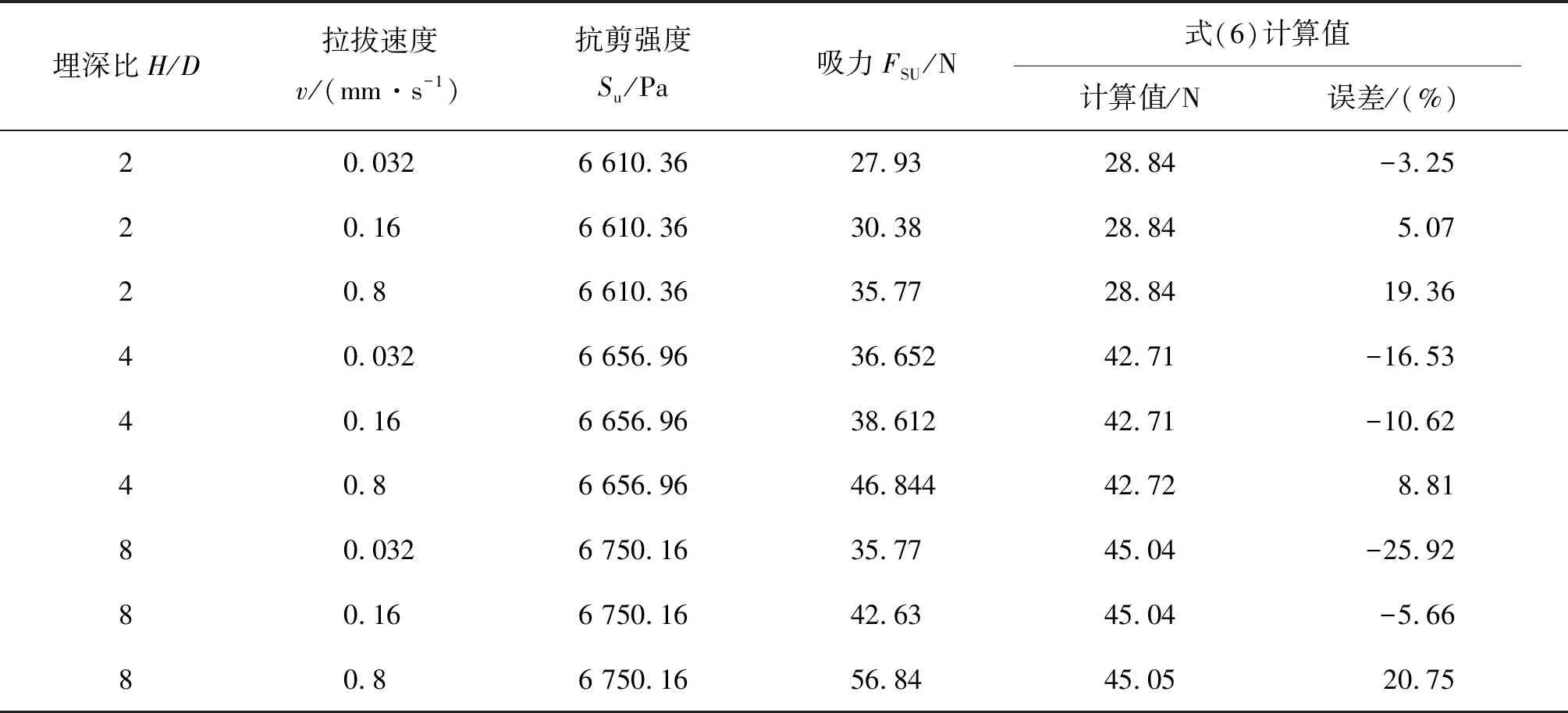
表5 Datta和Kumar[10]试验数据Tab. 5 Experimental data of Datta and Kumar

4 结 语

本次研究进行了光滑闭口短桩在水下黏性土中的垂向拔出试验，测量其底部腔体形态、压力以及拉拔力的变化情况，分析了上拔速度和埋深比对桩体底部压力的影响，可以得到以下结论：

1) 桩基在黏性土底床中上拔时，底部将产生负压吸力，该力可一定程度地增加桩基抗拔力；

2) 桩基在黏性土底床中上拔时，底部会产生孔隙水腔体，腔体在桩基上拔过程中由于负压的作用，不断被周围土体回填，使腔体大小保持相对稳定；

3) 在相同埋深比的条件下，桩基所受负压随上拔速度增大而增大，但上拔速度增大到一定值以后，其影响不再明显；相同上拔速度情况下，桩基受负压随埋深的增加而增大。

4) 提出了计算桩基在黏性土底床中垂直上拔时底部最大吸力的经验计算公式，并验证了该公式的准确性。