基于拓扑优化与多目标优化的集装箱相似畸变模型设计
刘佳琦,蔡忠华,王德禹
(1. 上海交通大学 海洋工程国家重点实验室,上海 200240; 2. 高新船舶与深海开发装备协同创新中心,上海 200240)
集装箱运输因其装卸货物效率高、运输时间短和成本低等优点,在航运市场得到广泛应用。目前,大约90%的非散装货物海运都是利用集装箱来完成运输[1]。随着集装箱的广泛使用,集装箱坠海事故发生率随之升高。据估计,每年海上运输过程中约有10 000个集装箱丢失[2],这对航运业造成了巨大的经济损失。Aguiar[1]等认为对集装箱堆垛进行动力学响应研究是探究集装箱丢失机理的方法之一。而目前,该项研究大部分是建立在有限元软件数值计算的基础上,这不能完全反映堆栈系统的真实特性。而在海运过程中,因受到模型体积大,试验难度大和成本高等多方面因素的限制[3],难以对高达几十米的集装箱堆垛进行试验测量。因此,在实验室条件下,利用相似模型来模拟集装箱,进而构建集装箱堆垛系统,并对其进行试验研究是可行的方法,不仅可以验证有限元数值模拟的准确性,还能得到堆垛系统最真实的力学行为。
模型试验研究方法是建立与原型相似的模型进行试验研究,从而揭示原型本质和规律的方法[4],其理论基础是相似定理。在设计集装箱相似模型时,由于集装箱具有薄壁构件(厚度与结构件最小平面跨度之比在1/80和1/5之间的构件[5]),若采用完全几何相似的缩尺模型进行试验,会出现相似模型的厚度太小而无法加工的情况,并且在加工焊接时极易产生初始应力和初始变形,这些初始缺陷可能会成为影响其结构力学行为的一个重要因素。初始缺陷影响系数的不一致代表了初始条件的不一致,这一点与相似第三定理相违背[6]。同时,集装箱原模型框架结构不是标准的型材制作,形状并不规则。除了框架结构,其它部分主要是采用蒙皮式波纹板结构,这种结构在实验室条件下很难制作。
鉴于集装箱结构的特殊性,本文提出了一种快速构建集装箱相似畸变模型的方法。首先,建立20英尺ISO货运集装箱有限元模型,基于有限元方法提取其静力学和动力学特征参数;其次,基于Froude缩尺定理确定缩尺集装箱特征参数目标值;然后,构建相似集装箱的结构模型,利用拓扑优化对缩尺集装箱墙壁结构的材料分布进行优化;最终,基于多目标优化算法对缩尺有限元模型的设计参数进行寻优直至寻优目标真值收敛至目标值,优化确定的缩尺有限元模型即为集装箱相似模型。最后采用有限元分析验证了该畸变相似模型的合理性。研究结果表明:本文的模型优化设计方法合理有效,设计的模型不仅满足模型的加工工艺要求,还能预测集装箱的力学行为。
1 20英尺ISO货运集装箱模型
标准20英尺ISO货运集装箱三维模型如图1所示,它的主要尺寸和材料参数信息[7]如表1所示。采用Patran有限元软件构建集装箱的有限元模型,模型的单元尺寸、形状和类型等详细信息见表2。缩尺模型与全尺寸模型在所有相似参数上完全相似是很难实现的。选择重要参数而忽略次要参数,虽然会导致畸变模型和原型之间产生误差[8],但误差的大小取决于选择参数对模型的影响程度。因此,选择对集装箱的机械性能影响较大的参数,包括:模型质量,惯性矩,结构刚度,第一阶模态频率,第一阶模态振型等作为重要参数。为了便于货物装卸,20英尺ISO货运集装箱采用了一端封闭,另一端双开门的结构形式,如图2所示。这导致开口端(开门端)和闭口端(封闭端)的横向刚度存在较大差异,需要分别考虑。
利用有限元分析获得20英尺ISO货运集装箱的主要特征参数,计算结果与Aguiar[1]等人保持一致,如表3所示。其中,集装箱的试验方法和要求如表4所示。

图1 20英尺集装箱结构示意Fig. 1 20-ft container structure diagram

图2 20英尺ISO货运集装箱Fig. 2 20-ft ISO freight container

表1 20英尺集装箱的主要尺寸和材料参数Tab. 1 Main size and material parameters of 20-ft container model

表2 20英尺集装箱有限元模型构造细节Tab. 2 Construction details of 20-ft container finite element model

表4 集装箱试验方法与要求[9-10] Tab. 4 Methods and requirements of container test[9-10]
2 20英尺ISO货运集装箱缩尺模型设计
2.1 相似设计准则
几何相似是指两个系统中相对应的几何要素的比值是一个常数。运动相似是指两个系统中对应的运动参数在时间上的相似性,比如速度、加速度等。几何相似和运动相似可以通过Froude缩尺准则来实现。动力学相似指作用于系统的力之间的比率是固定值。依据重力与惯性力之比,弹性力与惯性力之比两个无量纲数,来确定缩尺模型的物理(尺寸、质量)和结构(纵向、横向刚度)信息,使得缩尺集装箱与全尺寸集装箱在几何、运动、动力学方面的对应相似。其中,Froude 缩尺准则[11]信息如表5所示,其中,λ为缩尺比。

表5 Froude缩尺准则Tab. 5 Froude scaling law
2.2 缩尺模型的构造
大比尺模型虽然可以与实际的结构形式上更为相似,但是制作的成本更高,对试验环境的要求也越高,模型的装卸、测试都会有一定的困难。小比尺相似模型则因尺寸过小,不利于加工制造,且尺寸越小,因焊接产生的残余应力与初始变形对试验结果的影响会越大,导致试验结果的不准确。因此模型设计一方面应尽量做到与实际结构在各方面保持相似,另一方面还需要考虑模型制作的便利性和实验平台的限制等。本文为节约模型制作成本,降低对试验环境要求,取模型的缩小比例为1∶10,即λ=10。
相似模型的设计思路如图3所示。首先,基于有限元方法,建立20英尺标准海运干货集装箱结构1∶1的有限元模型,并提取其静力学和动力学特征参数目标值;然后,基于Froude定理确定缩尺集装箱静力学和动力学特征参数目标值;其次,在考虑加工制造限制的前提下,选定缩尺集装箱各结构构件的截面形式与尺寸,构建缩尺集装箱结构模型,利用拓扑优化对缩尺集装箱墙壁结构的材料分布进行优化,确定缩尺集装箱的墙壁结构形状。基于拓扑优化得到的集装箱结构形式,利用多目标优化算法对缩尺有限元模型的设计参数进行寻优,若目标真值无法收敛,则更改集装箱的各结构构件的截面形式或尺寸,重新进行拓扑优化与多目标优化,直至寻优目标真值收敛至目标值,优化确定的缩尺有限元模型即为集装箱相似模型。

图3 相似模型设计思路Fig. 3 Design way of similarity model
2.2.1 拓扑优化
为解决实验室条件下无法加工蒙皮波纹板结构的问题,利用平板进行替代。因加工水平的限制,在平板选择最小厚度,模型质量仍远远超过目标值。因此,需要利用拓扑优化对缩尺集装箱的墙壁结构的材料分布进行优化,在保证结构的特征性能前提下,最大程度地减轻模型的重量。载荷条件与约束条件对拓扑优化结果十分重要,因此,需要考虑在实际情况下集装箱的受力情况。

图4 载荷与约束条件Fig. 4 Load and constraints condition
20英尺ISO货运集装箱在实际使用期间,集装箱底部的4个角铸件通过扭锁固定在舱盖板或者下层的集装箱顶部,集装箱顶部的4个角承受着上层集装箱的重量和相邻的集装箱堆垛在集装箱长边方向和短边方向力的作用。因此约束条件为底部箱角完全固定,载荷条件为顶部的4个角分别受到沿集装箱长边、短边的集中力和垂直方向的压力作用,每个角在X,Y,Z三个方向上的力分别为75、1 077和150 N[9],具体的设置方式见图4。虽然在规范中,不同方向刚度试验底角件的固定方式存在差异,并非均为完全固定,但两者计算结果差异很小,在工程上可以忽略。
基于ABAQUS的SIMP拓扑优化方法,建立了以墙壁结构单元密度为设计变量,畸变能密度最小(刚度最大化)为目标函数,优化前后体积分数百分比和位移约束为约束函数的拓扑优化数学模型,对墙壁结构的材料分布进行优化。其中,对集装箱顶端箱角的四个点进行位移约束,以保证集装箱的箱角不会产生大变形。拓扑优化的数学模型为:
式中:F(ηi)表示结构的畸变能密度,ηi表示第i个单元的伪密度,α表示体积减小的百分比,V0表示为墙壁结构初始体积,D0表示节点的许用位移偏移值。
本文利用ABAQUS软件中变密度法对不同体积减小百分比和节点许用位移进行计算,随着体积减小分数与许用位移的不断减小,优化获得的墙壁结构趋于稳定(一致)。当选择α=5%,D0=0.02时,优化后的结构形式如图5所示。考虑到现实中加工制造的条件,对拓扑优化的结果进行修正,如图6所示。对修正后的集装箱模型进行静力学分析,得到结果与原始模型进行对比,见表6。

表6 模型优化结果对比Tab. 6 Comparison of model results

图5 拓扑优化结果Fig. 5 Results of topology optimization
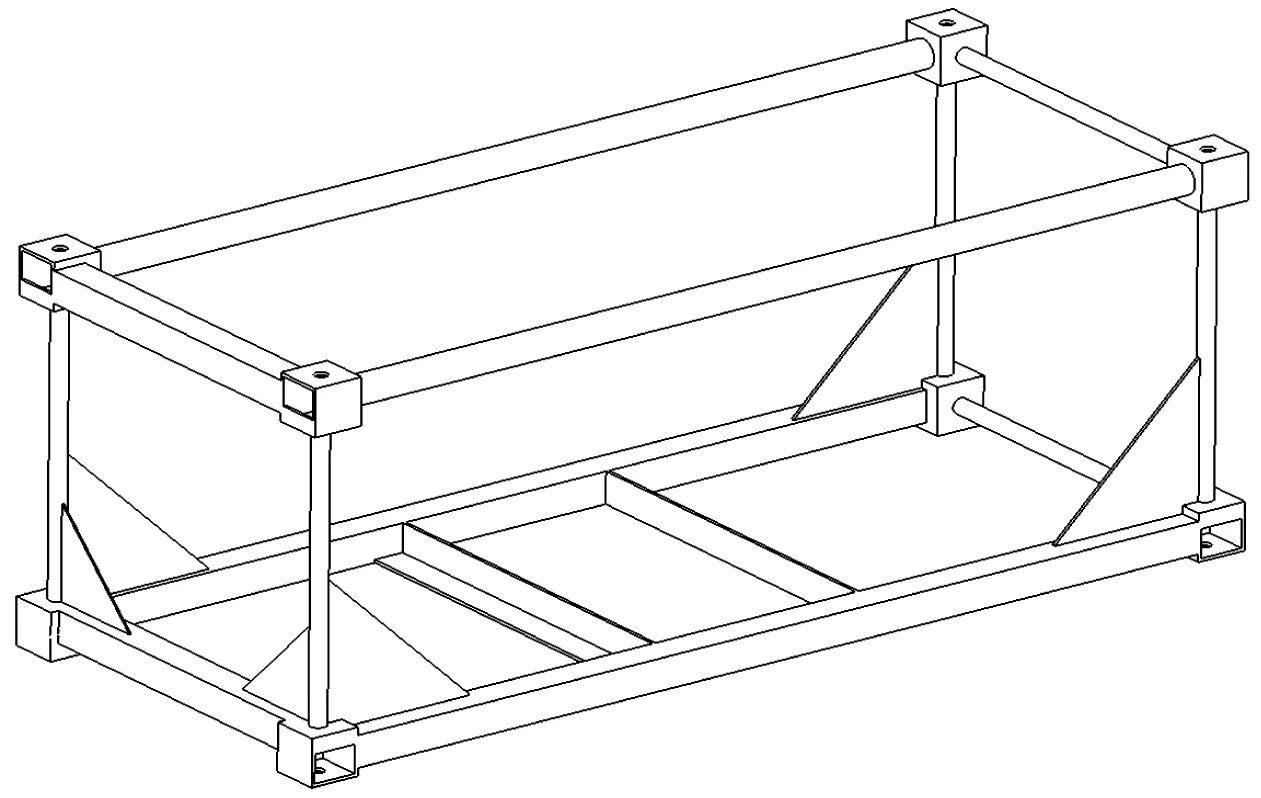
图6 20英尺缩尺集装箱几何图Fig. 6 Geometry diagram of 20-ft container
由分析结果可知,横向刚度(开口端)和纵向刚度均增加,横向刚度(闭口端)有所减小,优化区域的墙壁重量减小幅度达到91.6%。这表明,在集装箱底端加上小肘板可以很好地给予结构支撑。基于由拓扑优化确定的集装箱结构形式,进行多目标优化,以确定各个结构构件的厚度。
2.2.2 多目标优化
集装箱畸变相似模型的构建是一个多学科、多目标和多约束的优化问题。优化目标包括结构质量、集装箱的横向刚度(开口端和闭口端)、纵向刚度、抗侧刚度(开口端和闭口端)、一阶模态频率及振型。其中,采用静力学分析计算结构刚度,加载方式与边界条件信息详见表4。利用模态分析计算模态频率,并通过输出一些典型点(集装箱的8个箱角顶点)的位移来描绘振型,通过比较位移数值大小,初步判断缩尺模型与原尺寸模型在振型是否一致。最终,对缩尺模型进行模态分析,验证全尺寸模型与缩尺模型振型是否保持一致,以确保结果正确。约束条件包括结构强度和结构的可制造性等。结构强度的加载方式见表4。制造可行性表明该多目标分析的设计参数为离散型。本文采用逆向思维的设计方法,通过调整集装箱模型各结构构件的特征参数来满足设计目标。
运用多目标优化方法中的平方加权法将多目标优化问题转化为单目标优化问题,通过调节权重因子,来解决各目标之间的量纲不一致性问题。每个目标的权重因子为该目标值的倒数。采用多岛遗传算法对目标函数寻优求解。作为在传统遗传算法基础上建立的一种基于群体分组的并行性遗传算法[12], 算法将每个进化种群划分为若干个子种群,这些子种群被称为“岛屿”。在每个岛屿上对子种群独立地进行传统遗传算法操作,如选择、交叉、变异等,每个岛选定的个体定期转移到另一岛上,然后继续进行传统遗传算法操作,从而有效地抑制早熟现象,有利于找到全局最优解[13]。多岛遗传算法的优化模型流程见图7。

图7 多岛遗传算法流程Fig. 7 Flow diagram of multi-island GA algorithm
对集装箱缩尺模型进行模型修正。优化后的各个结构尺寸信息见表7。优化过程中变量变化曲线如图8和图9所示。

图8 优化过程中结构横向刚度曲线Fig. 8 Transverse stiffness curve in the optimization process

图9 优化过程中纵向刚度曲线Fig. 9 Longitudinal stiffness curve in the optimization process
应用Froude缩尺准则来获得缩尺模型的目标特征参数,选择的设计变量及名称见表7。通过建立数学模型来实现模型优化设计。可由下面的数学关系表示:


表7 缩尺模型几何信息特征Tab. 7 Scale model geometric information feature
3 20英尺ISO货运集装箱缩尺模型验证
缩尺集装箱模型材料采用普通碳素钢,其杨氏模量E=210 GPa,泊松比υ=0.3,密度为7 850 kg/m3。为了确定本文设计的缩尺集装箱模型的可靠性,采用有限元方法来对其进行验证。首先,对结构进行静力学强度分析,来提取模型的结构刚度。然后,对结构进行模态分析来确定模型的频率和模态特征。
3.1 静力学强度分析
对缩尺集装箱模型进行静力学强度分析的加载方式与边界条件,是参考CCS的《集装箱检验规范》[9]的内容设置的,详细信息见表4,利用有限元分析获得的刚度计算结果如图10所示。
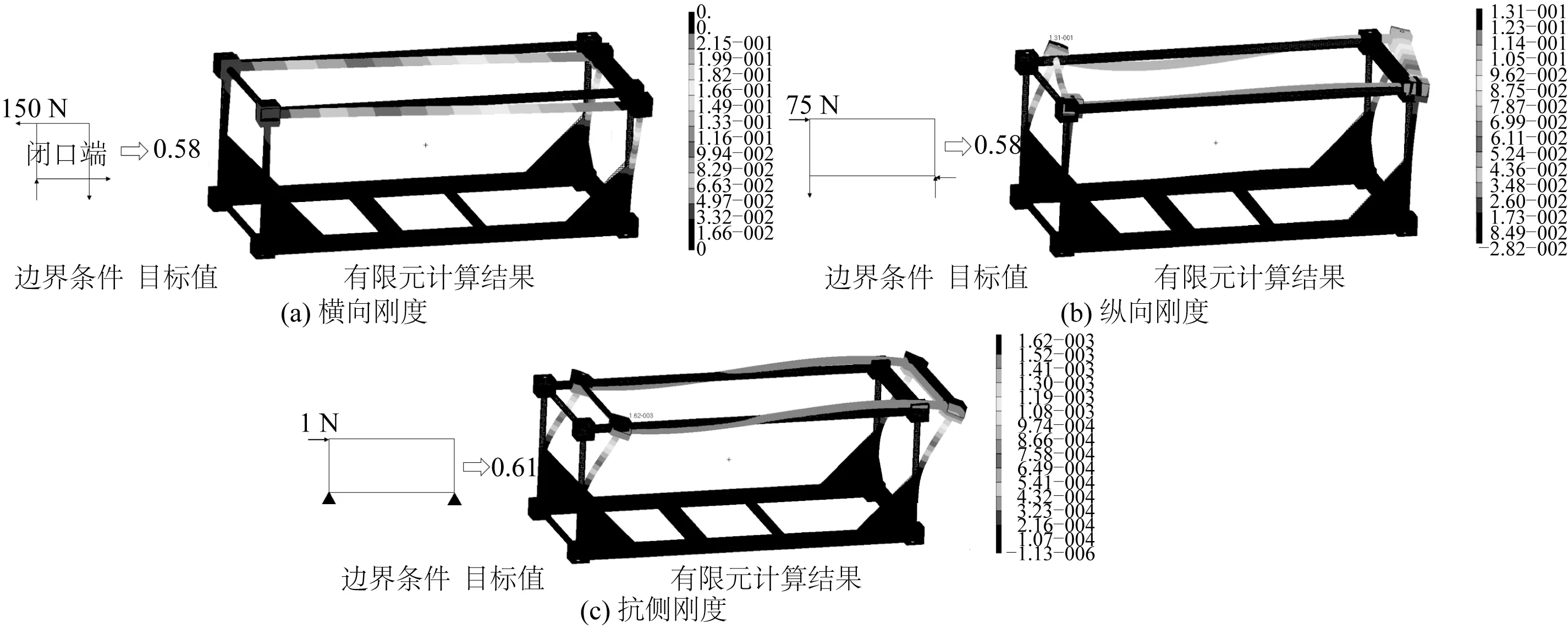
图10 缩尺集装箱刚度有限元计算结果Fig. 10 Finite element analysis results of stiffness of the scaled model
3.2 模态分析
对缩尺集装箱模型进行模态分析获得的结果如表8所示,一阶模态振型见图11。通过与原尺寸集装箱的一阶模态振型图对比,两者一阶模态振型一致,如图12所示。因此,缩尺集装箱的特征特性与由Froude缩尺准则获得的目标值保持一致,验证了经过多目标优化得到的集装箱缩尺模型的准确性与有效性。缩尺集装箱模型的详细参数信息见表9。

表8 前3阶集装箱模型模态频率 Hz Tab. 8 Former 3-order eigen frequencies of container model Hz

图12 全尺寸集装箱一阶模态Fig. 12 1st-order natural frequency
由表8可知,最终构建的相似模型与原型结构的之间的静力学行为差距较小,即本文所提出的方法可以有效减小原型结构和相似试验模型之间的差值,使计算结果满足预设目标的要求;从模态分析结果中可以看出,该集装箱相似模型与目标结果差距较小,满足目标要求,也验证了所提方法的可行性和实用性。

表9 缩尺集装箱模型参数信息表Tab. 9 Feature parameters of scaled model (λ=10)
4 结 语
基于Froude缩尺定理,结合拓扑优化与多目标优化,提出了一种构建相似畸变模型的方法。利用拓扑优化对缩尺集装箱墙壁结构的材料分布进行优化,利用多目标优化来寻求满足静力学目标、动力学目标和结构的物理特性时各个结构的设计参数值。并对具有薄壁结构的ISO海运集装箱进行相似畸变模型的构建。最终利用有限元分析验证了该相似畸变模型的合理性。结果表明:设计的模型不仅满足模型的加工工艺要求,还具有预测集装箱力学行为的能力。该设计方法也具有一定的通用性,能为其它类型结构相似模型的构建提供新的思路。

