电液式可变气门系统回油阶段瞬时压力的分析

吴学舜, 张洪川, 杜德峰, 韩志强, 赵家辉

(1. 西华大学 流体及动力机械教育部重点实验室, 四川 成都 610039; 2. 中国船舶重工集团有限公司第七一一研究所, 上海 201108)

柴油发动机可变气门技术可以根据发动机实际转速、工况及负荷的需要合理调节气门的启闭时刻和升程,与EGR、涡轮增压和高压喷射等新技术配合使用有助于HCCI,RCCI等新型燃烧模式的实施[1],同时能够合理组织缸内燃烧状态参数,以降低碳烟和NOx的排放[2].

由于电液式可变气门机构具有易于控制、响应灵活等优点而被广泛应用.但是由于电液式可变气门机构中存在液压系统,液压系统工作时会产生液体压力波动[3-4].压力波动会使液压系统产生震荡、噪声、液压元件的疲劳失效及空穴现象等,过早出现机械故障,缩短工件的使用寿命.同时,在电液式可变气门系统中,液压系统的压力波动还会导致液压腔的液压低于供油压力,使气门的运动规律出现暂时“失控”,从而影响配气机构的正常运行,使柴油发动机的燃烧和排放性能恶化,降低柴油发动机的整体工作性能[5].

针对电液可变气门系统实际工作过程中存在的液力延迟、机构响应等工作特性,众多学者展开了系列深入研究.M.POURNAZERI等[6]开发了一套滑阀式液压可变气门系统,根据试验数据建立了关键参数的数学模型,并根据该模型对液压可变气门系统的控制性、重复性等进行评估,结果表明滑阀式液压可变气门系统控制简单,且不受发动机转速的影响.XIE H.等[7]开发了一套汽油发动机电液可变气门系统,并基于自抗干扰控制概念,开发了混合扰动抑制控制策略,结果表明该策略能使可变气门系统较好地适应发动机转速和供油压力的变化.韩伟强等[8]划分了电液可变气门系统的工作周期,并对周期的特征时间及占比进行了研究,研究表明不同特征时间对控制参数的敏感性不同,通过优化系统的控制参数、合理选择气门附加升程有助于缩短系统的工作周期.许回江[9]研究了电液可变气门系统的气门升程特性,研究表明系统的结构设计对气门的开启、关闭速度起着决定性的作用.刘发发等[10]研究了电液可变气门系统的气门速度、加速度和气门升程波动等特性,研究表明合理控制液压油的供油压力与温度有助于改善系统的响应.韩志强等[11]划分了电液可变气门系统液压活塞腔内瞬时压力的波动周期,并研究了供油压力对周期特征参数的影响,研究表明供油压力对液压腔内瞬时压力的峰值、相位及持续时间的影响较大.杨忠炯等[12]研究了液压胶管出口压力波动特性,研究发现液压管长度对出口压力波动的影响大于液压管直径,随着流速增加,管径出口压力波动幅值逐渐减小,流体黏度对压力波动影响较小.孟育博等[13]研究发现使用滤波器可以有效降低压力波动的幅度.

综上所述,关键参数对船用柴油发动机电液可变气门系统液压油路瞬时压力的影响研究尚处于起步阶段,且少有文献探讨参数之间的相互作用对压力波动的影响.鉴于此,笔者结合自主设计研发的船用柴油发动机电液可变气门系统液压油路回油阶段的瞬时压力试验数据和仿真数据,研究回油电磁阀的开启斜率、最大开度、开启相位和供油压力等参数对电液可变气门系统液压油路回油阶段瞬时压力特征时间的影响,为合理控制液压系统压力波动提供理论支持.

1 电液式可变气门系统的建模与试验

1.1 仿真模型

图1为电液式可变气门系统油路模型示意图.为了减小液压油路瞬时压力波动带来的负面影响,进一步分析了电液可变气门系统电磁阀的开启斜率和供油压力对进回油电磁阀的阀后液压油路瞬时压力变化量的影响,笔者利用GT-SUITE软件建立了仿真模型,并对相关参数进行了仿真计算.仿真模型的系统动力学方程和流体力学方程遵循质量守恒原理、动量守恒原理和能量守恒原理,具体方程参考文献[14].

电液可变气门系统进油和回油的油路瞬时压力波动模型包括凸轮、挺柱、进油油路、回油油路和液压活塞腔等部分,模型中使用小孔模型代替电磁阀,通过对小孔孔径、启闭角度的设计来模拟电磁阀的工作;搭建蓄能器模型中的阻尼模块、蓄能器的质量模块和蓄能器组件中的弹簧模块模型来模拟平台中囊式蓄能器的工作;利用环形泄漏模型对活塞与活塞套之间液压油的泄漏量进行计算.由于配气机构的摇臂比为1.5,即气门附加升程是液压活塞升程的1.5倍,因此模型中略去摇臂及气门组件,通过液压活塞的升程乘以摇臂比便得到相应的气门附加升程.

图1 电液可变气门系统油路模型

1.2 可变气门系统平台试验验证

为了验证电液式可变气门系统油路模型的准确性，在课题组自主设计研发的船用柴油发动机电液式可变气门系统试验平台上进行瞬时压力测试.船用柴油发动机电液式可变气门系统的试验平台如图2所示.

图2 电液可变气门系统试验平台

试验平台主要由控制系统、供油系统、数据采集系统和驱动系统4部分组成.平台详细的工作原理和控制逻辑详见文献[14].

1.3 测试传感器及设备的规格和精度

为了保证试验数据的精度和可靠性,需要对测量设备的规格和主要参数进行考察,结果见表1.

表1 主要测试传感器及设备信息和主要参数

1.4 电液可变气门系统工作时序

电液可变气门系统工作时序见图3,以光电编码器发出的同步信号为基准,确定电磁阀的控制时序.当电磁阀收到ECU发出的电磁阀开启信号,进油阀芯开启,液压油经电磁阀进入可变气门机构液压腔,并推动液压活塞开启气门附加升程;液压油的进油持续期(即电磁阀的进油脉宽)决定了进入液压腔内的液压油量.电磁阀进油脉宽结束时进油阀芯关闭,此时液压腔与电磁阀间的液压油路封闭.

图3 电液可变气门系统工作时序

该过程中电磁阀的保持过程持续时间即为保持脉宽.该过程中气门的附加升程几乎保持不变.保持脉宽结束后电磁阀回油阀芯开启,电磁阀回油阀芯从开启到关闭的持续时间为回油脉宽,可变气门液压腔里的液压油经电磁阀流回液压油箱.为使液压腔内的液压油完全泄出,电磁阀的回油脉宽应不小于进油脉宽.

1.5 电液可变气门系统试验的验证

液压油路瞬时压力试验值与仿真值的对比结果如图4所示.

图4 液压油路瞬时压力仿真值与试验值对比

图4显示瞬时压力试验值与仿真值具有良好的一致性,说明所建模型能够用于分析关键参数对系统液压油路回油阶段的瞬时压力变化特征时间的影响.仿真模型主要参数及其设置数值如表2所示.

表2 仿真模型主要参数及设置数值

1.6 回油阶段瞬时压力特征时间的定义

电液可变气门系统中电磁阀阀后液压油路瞬时压力、最大开度和附加升程随时间变化曲线如图5所示.以回油电磁阀开启始点(a点)作为回油阶段瞬时压力的始点,以瞬时压力消失点(d点)作为回油阶段瞬时压力的末点.将回油阶段瞬时压力分为压力急降区(ab)、压力稳定区(bc)和压力自由下降区(cd).

图5 瞬时压力、最大开度和附加升程随时间变化曲线

电磁阀阀后液压油路回油阶段瞬时压力的特征时间定义如下: ①tab为瞬时压力急降区的时间,电磁阀开启始点至瞬时压力平衡始点,液压油在气门弹簧力作用下流回液压油箱,管内瞬时压力急剧下降; ②tbc为瞬时压力稳定区的时间,电磁阀保持最大开度,液压油依然在气门弹簧力作用下流回液压油箱,管内瞬时压力保持稳定; ③tcd为瞬时压力自由下降区的时间,电磁阀保持最大开度,此时气门附加升程完全消失,液压油在惯性作用下流回液压油箱,管内瞬时压力下降至0.

2 结果分析

基于进油电磁阀各参数数值不变,通过改变回油电磁阀的开启斜率k、最大开度d0、开启相位β和液压油的供油压力来研究关键参数对回油阶段瞬时压力特征时间的影响.电磁阀结构参数之间的关系公式为

d0=kβ+b，

(1)

式中:b为系数.

2.1 开启斜率与供油压力对瞬时压力的影响

根据式(1),保持回油电磁阀的最大开度为4 mm、开启相位为435°和开启斜率为0.3不变,不同供油压力p′下,液压油路瞬时压力的变化曲线如图6所示.保持最大开度为4 mm、开启相位为435°和供油压力为12 MPa不变,不同开启斜率k下,电磁阀阀后瞬时压力的变化曲线如图7所示.

不同开启斜率下,特征时间tab随供油压力变化曲线如图8所示.由图8可知:开启斜率不变,液压油供油压力对tab的影响可以忽略;供油压力不变,tab随开启斜率的增加而减小.

由图6可知:不同供油压力下,液压管内急降区ab的瞬时压力几乎一致;由p=FS(其中p为压力,F为作用力,S为面积)可知:由于液压系统中液压油的压力与单位面积所受的作用力和流通面积有关,所以当电磁阀的开启斜率、最大开度和开启相位固定不变后,管内液压油流动过程中获得的动能一致,即液压油的流动状态也已经确定,液压油的流速不变,所以tab几乎不受供油压力的影响.

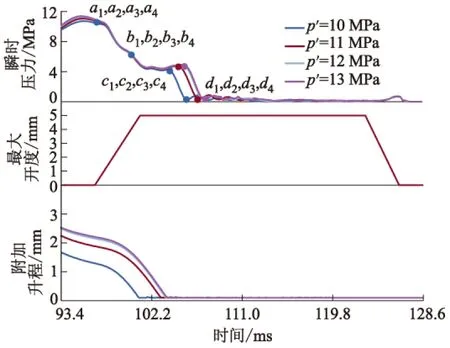
图6 供油压力对瞬时压力的影响

图7 开启斜率对瞬时压力的影响

由图7可知:液压管内急降区ab同一时刻的瞬时压力均随开启斜率的增加而减小,且管内瞬时压力在任意时刻均有Fmax/Fmin<1.68;在电磁阀完全开启之前,阀口处的流通面积均有Smax/Smin>1.76;结合管内的瞬时压力和电磁阀流通面积,由p=FS可知,开启斜率越大,液压油流动过程中获得的动能越大,液体流速越快,所以tab随开启斜率的增加而减小.

不同开启斜率下,特征时间tbc随供油压力变化曲线如图9所示.由图9可知:开启斜率不变,tbc随供油压力的增加而增加;供油压力不变,tbc随开启斜率的增加而增加,开启斜率k≥0.20时,k对tbc的影响较小.

图8 不同开启斜率下,tab随供油压力变化曲线

图9 不同开启斜率下,tbc随供油压力变化曲线

由图6可知:不同供油压力下虽然稳定区bc的瞬时压力几乎一致,但同一时刻的气门附加升程随供油压力的增加而增加,由于课题组开发的可变气门机构采用液压活塞式,气门附加升程越大,液压活塞腔内储存的液压油越多,所需泄油时间越长,所以tbc随供油压力的增加而增加.由图7可知:电磁阀在稳定区bc处于全开状态,液压管内稳定区的瞬时压力几乎相等,所以由p=FS可知:k≥0.20时,k对tbc的影响较小;k=0.15时急降区ab流出的液压油较多,对应稳定区的液压油较少,所需时间较短.

不同开启斜率下,特征时间tcd随供油压力变化曲线如图10所示.由图10可知:特征时间tcd均约为2 ms,几乎不受供油压力和开启斜率的影响.由图6,7可知:自由下降区cd的附加升程已完全消失,管内残余液压油在惯性作用下流出,不同供油压力或开启斜率下,管内瞬时压力初始值几乎相等,由p=FS可知,tcd不受开启斜率和供油压力的影响.

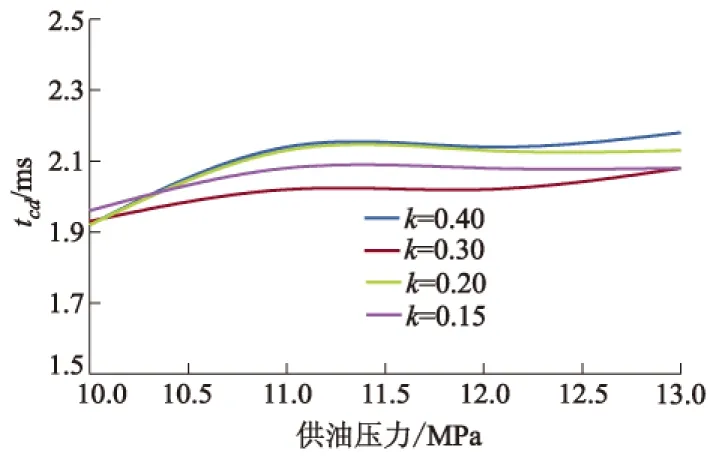
图10 不同开启斜率下,tcd随供油压力变化曲线

2.2 最大开度和供油压力对瞬时压力的影响

根据公式(1),保持回油电磁阀的开启斜率为0.3、开启相位为435°和供油压力为12 MPa不变,不同最大开度d0下液压油路的瞬时压力随时间变化曲线如图11所示.

图11 最大开度对瞬时压力的影响

回油电磁阀不同最大开度下,供油压力对特征时间tab,tbc和tcd的影响如图12-14所示,具体的讨论分析与2.1小节中供油压力对特征时间的影响类似,不再阐述.

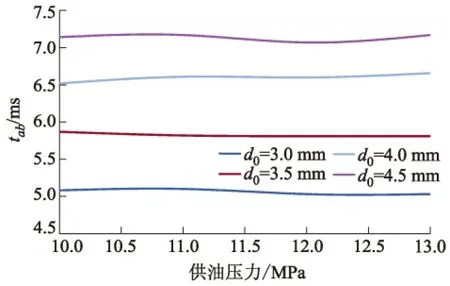
图12 不同最大开度下，tab随供油压力变化曲线

由图12可知,供油压力不变,tab随最大开度d1的增加而增加.由图11可知:d0≤3.0 mm时,急降区ab的瞬时压力变化曲线一致;d0>3.0 mm时,d0越大,其额定流量越大,所需液压油的量越多,充油时间越长,瞬时压力达到稳定阶段所需的时间越长,所以tab随d0的增加而增加.

图13 不同最大开度下，tbc随供油压力变化曲线

由图13可知,供油压力不变,tbc随最大开度d0的增加而减小.由图11可知:此时电磁阀全开,虽然稳定区bc的供油压力均随d0的增加而减小,但d0的变化对液压油瞬时流量的影响大于管内供油压力变化对液压油瞬时流量的影响,所以tbc随d0的增加而减小.

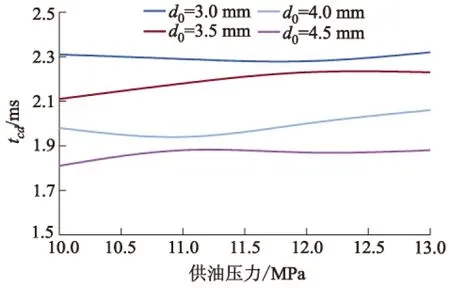
图14 不同最大开度下，tcd随供油压力变化曲线

由图14可知,供油压力不变,tcd随最大开度d0的增加而减小.由图11可知:此时气门附加升程消失;液压油在惯性作用下流回油箱,回油电磁阀在不同d0下,瞬时压力初始值均有Fmax/Fmin<1.16、电磁阀流通面积均有Smax/Smin>1.27;由p=FS可知:当电磁阀的开度越大时,电磁阀的流通截面越大,此时的液压油流速越快,故液压油获取的动能越大,tcd随d0的增加而减小.

2.3 开启相位和供油压力对瞬时压力的影响

根据式(1),保持回油电磁阀的最大开度为4 mm、开启斜率为0.15和供油压力为12 MPa不变,不同开启相位β下,液压油路的瞬时压力随时间变化曲线如图15所示.

图15 开启相位对瞬时压力的影响

回油电磁阀不同开启相位下,供油压力对特征时间tab,tbc和tcd的影响如图16-18所示,具体的讨论分析与2.1小节中供油压力对特征时间的影响类似,不再阐述.

图16 不同开启相位下,tab随供油压力变化曲线

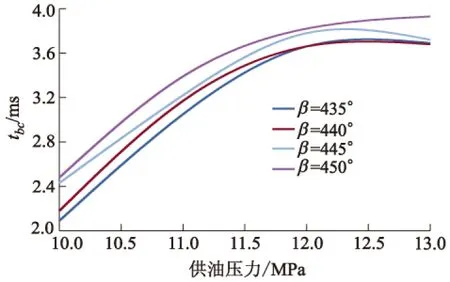
图17 不同开启相位下,tbc随供油压力变化曲线

图18 不同开启相位下,tcd随供油压力变化曲线

由图16,18可知,供油压力不变,不同开启相位下,tab均在5.1 ms附近,tcd值均在2.0 ms附近,且tab和tcd的波动幅度均小于0.2 ms.由图15可知,开启相位只是改变了管内液压油的泄油时刻,而对电磁阀自身的结构参数没有任何改变,所以电磁阀开启相位对tab和tcd的影响可以忽略.

由图17可知,供油压力不变,tbc随开启相位的滞后略有增加,但不同开启相位下tbc之间的差值均小于0.3 ms.由图15可知:稳定区间bc的供油压力随开启相位的滞后略有减小;由此p=FS可知,开启相位越滞后,液压油获取的动能越小,流动过程所需时间越长,所以tbc随开启相位的滞后而略有增加.

3 结 论

1) 特征时间tab随回油电磁阀开启斜率的增加而减小,随最大开度的增加而增加;特征时间tbc随回油电磁阀开启斜率的增加而增加,随最大开度的增加而减小;回油电磁阀开启斜率和最大开度对特征时间tab和tbc的影响大于开启相位和供油压力;特征时间tcd几乎不受回油电磁阀开启斜率、最大开度、开启相位和供油压力的影响.

2) 开启斜率和最大开度对回油系统的影响大于开启相位和供油压力,因此在有效调控压力波动时,可优先调整电磁阀的开启斜率和最大开度,达到系统最有利的工作状态.