基于激光雷达数据的仓储物流AGV障碍物识别方法

吴 飞, 黄 威

(武汉理工大学 机电工程学院, 湖北 武汉 430070)

随着电子商务、物流、计算机等行业近年来的迅猛发展,消费升级下的市场压力变大,传统的仓储运行模式已难以满足海量库存管理、提高运行效率及降低人力成本等需求.自亚马逊将Kiva机器人运用到仓储物流中以来,针对智能仓储的运行模式、任务调度、AGV定位和多AGV路径规划等理论方法在一定程度上使得智能仓储系统更加可靠、更有效率[1].

研究人员在路径规划与避碰方面提出了许多解决方案.例如,对货架和任务选取设定规则来减少拥堵[2];引入线性时序逻辑理论,来优化任务分配和路径[3];使用带时间窗的多AGV路径规划算法,减少多台AGV发生碰撞的可能性等[4-5].

然而在实际运行的过程中,不可避免地会出现外界干扰和运行产生定位误差等情况,这些情况导致的误差会随时间不断累积,使得原本完美的多AGV多路径规划出现偏差直至失效.另外,AGV运行也可能会产生一些故障而无法移动,导致整个系统无法按照原本的规划运行.

通过分析智能仓储的运行环境,仓储物流AGV可能出现的冲突以及前方障碍物类别可归纳为以下几种情况: ① 两个AGV由于累积误差可能在交叉路口出现争夺路口通行优先权的情况,导致两个AGV互相成为对方的障碍物; ② 某个AGV由于故障在通行道的某处停止运行,导致AGV占用通道而成为障碍物; ③ 货架被错误地放置在了通道上而成为障碍物; ④ 原本货架上的货箱掉落在通道上而成为障碍物; ⑤ 智能仓储维护人员作业时占用通道而成为障碍物.

通过上述的几种情况,可以看出不同的障碍物对正常运行的AGV影响不同.占用通道的货箱和货架为永久障碍物,需AGV重新规划路径,需人为干预将障碍物清除;人和AGV则可能为临时障碍物,只需等待一小段时间即可继续通行,不必重新规划路径,也不必申请人为干预来清除.

鉴于此,在智能仓储环境中,研究使用2D激光雷达数据识别AGV前方障碍物的方法,为AGV后续的精准决策提供基础.

文中以激光雷达数据为基础,提出了改进DBSCAN算法以及障碍物轮廓特征提取方法,使用粒子群优化参数后的SVM算法对障碍物进行识别.

1 数据预处理

由于通过激光雷达感知来避碰的范围仅限数秒后可能的碰撞,因此AGV感知障碍物的警戒区设定为1 200 mm的范围内.根据所用的RPLIDAR A2型号激光雷达测量范围以及划分的警戒区域范围,激光雷达数据在距离上的分布如表1所示.

表1 距离分布表

为滤除激光雷达数据中的噪声数据,需要用到聚类的算法将目标障碍物分离出来.由于不需要预先指定数据中的目标数,在障碍物数目不确定的智能仓储环境下,基于密度的DBSCAN算法相较于其他聚类算法鲁棒性较高.然而,激光雷达的数据密度并不均匀,靠近激光雷达的数据较密集,而远离激光雷达的数据较稀疏[6].因此,提出了一种自适应邻域半径的DBSCAN算法来解决此问题.

经典的DBSCAN算法[7]通过一组邻域参数(ε,MinPts)来描述样本分布的紧密程度.在算法流程中先根据事先指定的一组邻域参数(ε,MinPts)来遍历样本集以找到所有的核心对象,再随机地选取一个核心对象找到其密度可达的所有样本点,这些密度可达的样本点为一个聚类簇,直至所有核心对象均被访问过为止.其中核心对象是其邻域ε内至少包含MinPts个样本点的样本点.

在改进的DBSCAN算法中,设定的邻域半径ε是激光雷达最小测量距离dmin处所对应的邻域半径值,样本点xj处的极径为ρj,则其自适应邻域半径为

(1)

在经典DBSCAN聚类算法流程中用εj代替ε作为邻域半径来判断样本点是否为核心对象,即核心对象是其邻域εj内至少包含MinPts个样本点的样本点.

2 障碍物特征参数提取

为了对聚类后的聚类簇进行识别分类,将激光雷达数据特征设计为以下的特征参数: ① 聚类簇ci中包含的点集个数ki; ② 聚类簇ci中各点距离值的平均值：

(2)

③ 聚类簇ci中第1个点和最后一个点的连线所在的直线为li,ci中第j个点为点Pij,其中j∈{1,2,…,ki},点Pij中距离直线li距离最大的点为点Pim,其中m为该点的聚类簇ci中的序号且m∈{2,3,…,ki-1},点Pim与点Pi1连线所在的直线为li1m,点Pim与点Piki连线所在的直线为likm,如图1所示.

图1 特征提取方法示意图

聚类簇ci中第1到m个点中,偏离直线li1m的距离值的标准差为

(3)

聚类簇ci中第m+1到ki个点中,偏离直线lmk的距离值的标准差为

(4)

总标准差为

(5)

④点Pi1与点Piki及点Pim这3个点的外接圆圆心为点Oi,外接圆半径为ri,如图1所示.聚类簇ci中各点偏离上述外接圆圆弧的距离标准差为

(6)

因此,聚类簇ci的特征向量:

(7)

一帧激光雷达数据可由特征向量C表示,C=[C1,C2,…,Cn],其中n为激光雷达数据完成聚类后的簇数.

3 基于粒子群算法的支持向量机

3.1 支持向量机原理

支持向量机(support vector machine, SVM)是一种定义在特征空间上间隔最大的二分类模型[8-10].

假设特征空间上的训练数据集为

T={(x1,y1),(x2,y2),…,(xN,yN)},
xi∈Rn,yi∈{+1,-1},i=1,2,…,N.

(8)

SVM算法是在特征空间中找到一个能将实例分成不同类的分离超平面.当数据为线性可分时,SVM的目标是求出几何间隔最大的分离超平面;当数据线性不可分时,在优化问题中引入松弛变量ξi≥0,SVM的目标变为最优化引入松弛变量后的目标函数;当数据是非线性时,引入核函数将数据映射到高维空间,SVM的目标变为寻找高维空间中的分离超平面.假设核函数为K(xi·xj)=φ(xi)·φ(xj),非线性SVM的最终优化的目标函数为

0≤αi≤C,i=1,2,…,N.

(9)

分类决策函数为

(10)

最常用且适用范围最广的核函数为径向基核函数,其核函数如下：

K(x,z)=exp(-γ‖x-z‖2).

(11)

使用径向基核函数时,需提前确定惩罚参数C和核参数γ的值,文中使用粒子群优化算法来确定.

3.2 粒子群算法原理

粒子群优化算法[11-12]是根据鸟类觅食行为提出的全局最优化算法，其流程如图2所示.

图2 粒子群算法流程图

在优化过程中,每个粒子都会根据当前适应度最高的粒子来更新自己的速度和位置.具体方程如下:

vij(t+1)=ωvij(t+1)+c1r1(t)(pij(t)-

xij(t))+c2r2(t)(pgj(t)-xij(t)),

(12)

xij(t+1)=xij(t)+vij(t+1),

(13)

式中:vij表示粒子的速度;ω是惯性权重;xij是当前粒子的位置;pij表示第i粒子找到的最优解;pgj表示当前的全局最优解;r1与r2表示区间(0,1)内的均匀随机数;c1与c2是学习因子.

4 试验分析

4.1 数据采集

根据智能仓储环境下障碍物种类分析结果,智能仓储中AGV前方障碍物主要分为人、货箱、货架和执行其他任务的AGV共4种.为采集障碍物相应的激光点集数据,搭建了智能仓储模拟环境.模拟环境中,“障碍物”人与真实环境一致;纸箱模拟真实环境中的货箱;由于激光雷达采集的数据为障碍物距离地平面一定距离的平面轮廓特征,货架则由具有相似底部支撑结构的椅子模拟;仓储物流AGV和采集数据的AGV则是由bobac机器人模拟;激光雷达为RPLIDAR A2型号激光雷达.搭建的智能仓储的模拟环境如图所示3,在模拟环境中采集并去除运动畸变后的激光雷达数据如图4所示,为显示方便,这里只显示了距离在1 200 mm以内的数据.

图4中,60°至135°范围内为人(腿)对应的激光雷达数据;0°至60°范围内为货箱(纸箱)对应的激光雷达数据;300°至360°范围内为货架(椅子)对应的激光雷达数据;225°至300°范围内为AGV对应的激光雷达数据.

采集数据的AGV在如图3所示的智能仓储模拟环境中,采集得到800帧去除运动畸变后的障碍物试验数据,每一帧数据包含一种典型障碍物.其中人(腿)、货箱(纸箱)、货架(椅子)和AGV这4种典型障碍物的样本数量分别为200.在试验中,4种典型障碍物随机选出30%的数据,即60组,一共240组数据作为测试样本,其余的70%,即560组数据为训练样本.

图3 智能仓储模拟环境图

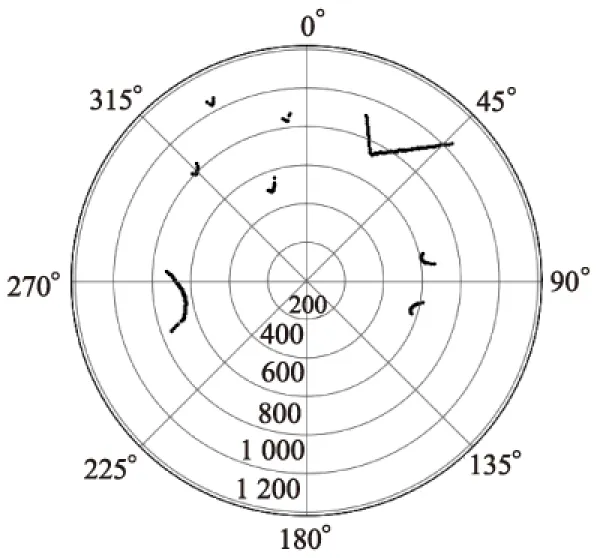
图4 激光雷达采集数据图

4.2 特征参数提取

根据文中提出的数据预处理方式和改进后的DBSCAN算法，对激光雷达数据进行滤波与聚类，最终得到的聚类簇作为训练与测试用的数据样本.使用文中提出的障碍物特征参数提取方法，计算出每一个聚类簇数据样本的特征向量，部分结果如表2所示.由于特征参数k为数据样本所包含点的个数，表中用整数表示，特征参数则保留小数点后4位有效数字.

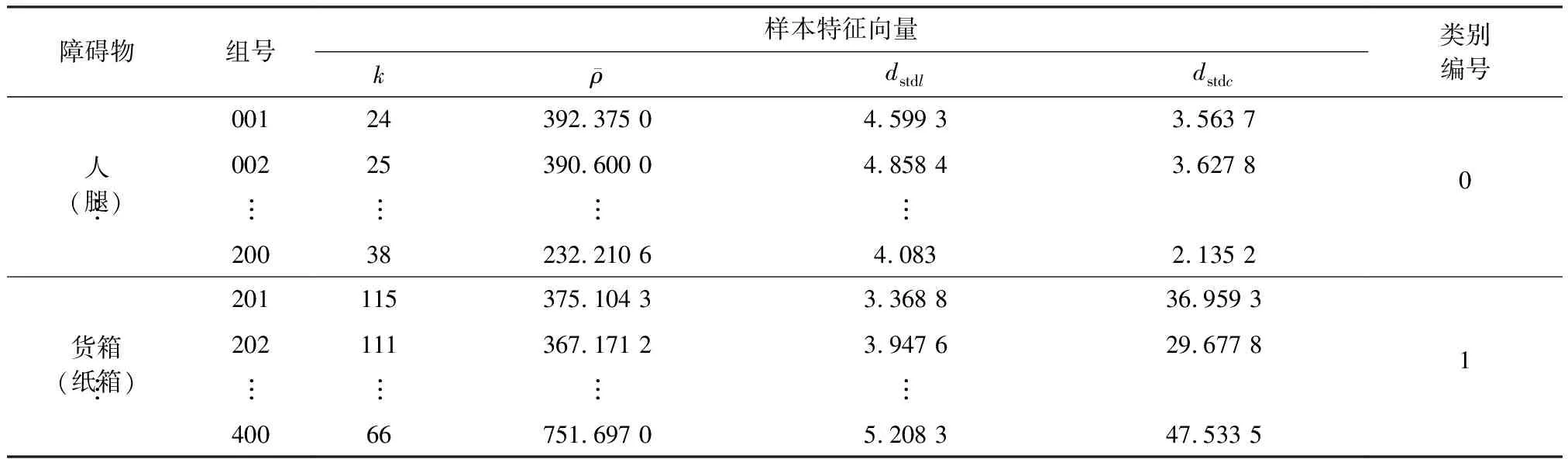
表2 训练样本特征向量表

(续表2)

4.3 粒子群算法寻找最优参数

径向基核SVM算法的参数包括惩罚参数C和核参数γ.其适应度定义为训练集上使用5折交叉验证的准确率.使用粒子群算法寻找最优参数时,粒子种群规模选为100,迭代次数为50,学习因子c1=c2=2.粒子群优化径向基核SVM参数所得到的最优适应度曲线如图5所示.

图5 粒子群最优适应度曲线

迭代次数完成后,最优适应度结果为0.978 57,参数C=4.617 00,γ=0.012 87.

4.4 结果分析

在训练集上寻找到了最优的参数并训练好模型后,还需在测试集上对预测分类的效果进行测试.径向基核SVM算法默认参数(C=1.0,γ=0.25)和PSO优化后参数在测试集上的混淆矩阵如图6和图7所示.

由图6和7中的混淆矩阵可以得到识别正确率如表3所示.

图6 默认参数分类混淆矩阵

图7 粒子群优化参数分类混淆矩阵

表3 正确率对比表

由表3可知,在对4种典型障碍物进行识别分类时,默认参数下的径向基核SVM算法识别正确率为66.25%,经过PSO优化参数后的径向基核SVM算法识别正确率达到了94.58%.证明了使用提出的特征提取方法以及粒子群优化的径向基核SVM对智能仓储中典型障碍物识别有良好的效果.

5 结 论

1) 提出了一种针对激光雷达数据的DBSCAN算法的改进方式,并成功将其运用在激光雷达数据的预处理中.

2) 提出使用粒子群优化算法寻找径向基核函数SVM的参数,在测试集上的结果表明,使用粒子群优化算法优化参数后的径向基核函数的识别效果远好于优化之前的效果.其结果证明了提出的特征提取方法以及粒子群优化的径向基核SVM算法适用于基于激光雷达数据的智能仓储典型障碍物识别.