基于侧倾角预测的坡地作业机具悬挂自适应控制

陈 晨, 夏长高, 韩江义, 杨宏图

(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)

普通的机具悬挂系统在侧向坡度特征明显的山地条件下耕作时无法完成调整机具悬挂姿态角的功能,易产生左右耕作深度不均匀的问题,大大影响了山地地形的耕作质量,因此研究具有坡地适应性的机具悬挂系统就显得尤为重要.目前,相关专家学者已经对坡地自适应悬挂系统进行了一些卓有成效的研究.K. HIRASAWA等[1]通过试验和模型预测的比较,推断出土粒的高度和土壤堆积的形状,并以此为基础对拖拉机悬挂系统的作业工况进行了研究.周浩等[2]提出了以地表平整度和耕深作为电控液压悬挂耕作性能的评价指标,并以此评价了旋耕机的旋耕效果.这些研究为电控液压悬挂仿真建模以及耕作效果评价提供了借鉴.郝希阳等[3]设计了一种新型拖拉机电控液压悬挂系统,提高了实际耕深的控制精度.徐煌[4]改进了传统的电控液压悬挂系统,并在此基础上优化了液压管路.这些研究对液压系统结构进行了优化,进一步提高了电控液压悬挂耕深的控制精度.胡炼等[5]建立了液压缸活塞伸缩长度与农机具相对拖拉机倾斜角度的转换函数关系,利用调平油缸活塞的行程信号估计悬挂机具的实际侧倾角,为电控液压悬挂的实际侧倾角估计提供了一种方案.

目前,许多学者已经对拖拉机电控液压悬挂的耕深控制进行了较为深入的研究[5-6],但是针对电控液压悬挂侧倾角控制的研究还相对较少.因此,文中在现有电控液压悬挂反馈控制系统的基础上提出了根据拖拉机车身姿态实时预测悬挂机具侧倾角的方法.基于拖拉机机身姿态角与机具悬挂侧倾角间的空间状态方程,设计机具悬挂姿态角的状态估计器,预测机具侧倾角.文中设计了模糊控制器对侧倾角进行跟踪,最终实现对电控液压悬挂机构侧倾角的控制.

1 机具侧倾角估计预测方法

在实际耕作条件下,拖拉机拖动后部挂接于电控液压悬挂的农具进行耕作,当拖拉机机身经过具有某侧向坡度的路面后,耕作农具此后也将经过该路面.因此,拖拉机车身与拖拉机机具悬挂在耕作路径上的地形具有相似性,机具悬挂侧倾角与拖拉机机身侧倾角间存在纯滞后关系,可以通过测量拖拉机姿态角预测悬挂机具侧倾角.

在测量拖拉机姿态角时,文中采用了由磁强计与加速度计融合的传感器方案,该方案将磁强计与加速度计融合模块安装于拖拉机车身质心位置,通过磁强计与加速度计2种信号的融合,实时获取拖拉机车身的侧倾角.

图1为拖拉机姿态角测量方案示意图.图1中建立了2个坐标系.导航坐标系n为OENV右手坐标系,其原点在拖拉机质心处,E轴指向地球东,N轴指向地球北,V轴与E轴、N轴相互垂直.拖拉机坐标系b原点始终与导航坐标系n原点重合,Y轴指向拖拉机前端,X轴在水平面内指向右端,Z轴与X轴、Y轴相互垂直.

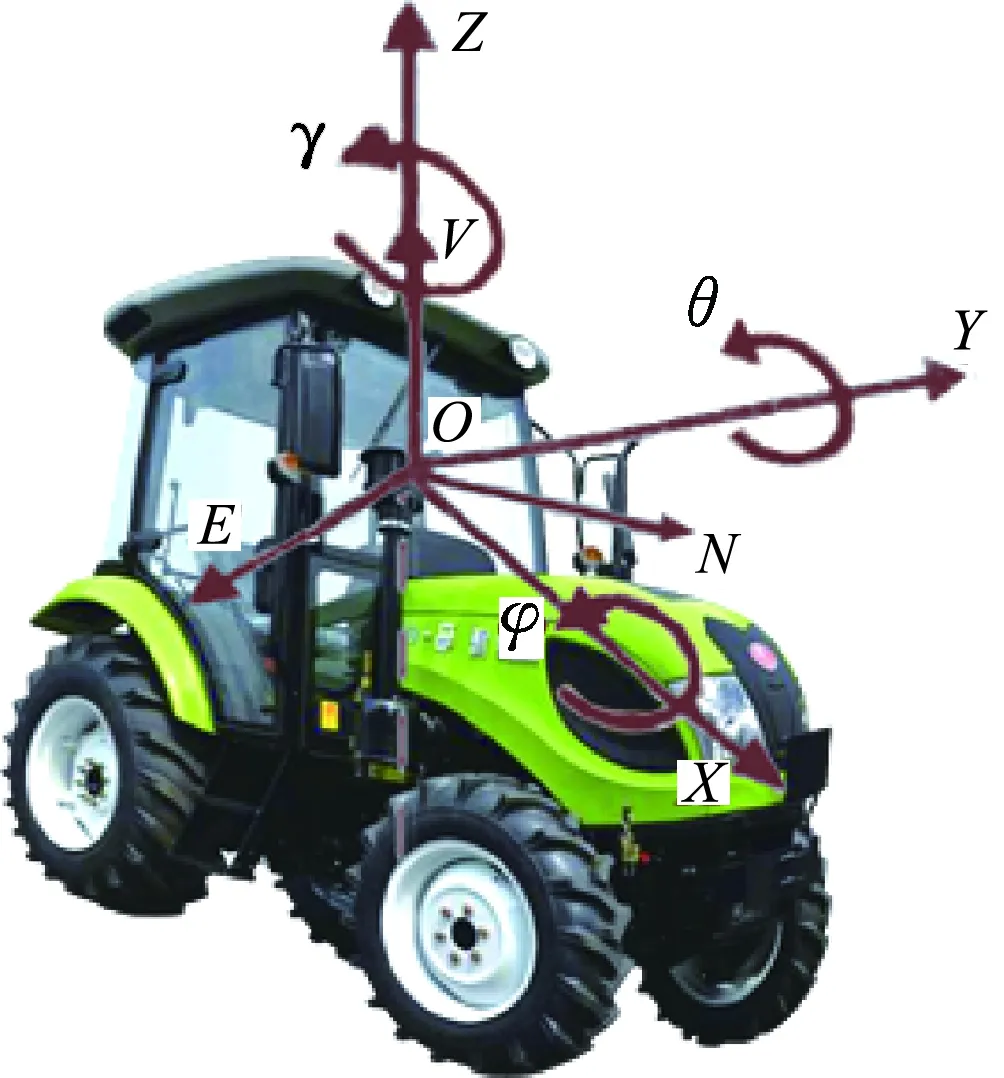
图1 拖拉机姿态角测量方案示意图

根据磁强计与加速度计获得的传感器测量信号文中采用下列方法对传感器信号进行融合.

假设当拖拉机在导航坐标系中处于静止状态、且拖拉机坐标系b与导航坐标系n相重叠时,车载加速度计与磁强计的输出在导航坐标系n下为An和Mn,即

(1)

式中:g为重力加速度;mnN和mnV分别为地磁场在导航坐标系的北向分量和垂向分量.

当拖拉机处于某种姿态时,拖拉机坐标系b中,车载加速度计与磁强计的输出为Ab和Mb可表示为

(2)

根据拖拉机加速度计和磁强计在拖拉机坐标系b与导航坐标系n之间的转换关系,可得

(3)

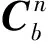
(4)

同时由导航坐标系n与拖拉机坐标系b的定义,可得到两坐标间的坐标转移矩阵T为

(5)

(6)

式中:φ为拖拉机航向角;θ为拖拉机俯仰角;γ为拖拉机侧倾角.

(7)

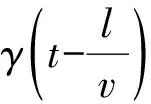
由于式(7)为非线性方程,在研究上很不方便.考虑到传感器与拖拉机农具间的距离很短,属于小延迟环节,因此将该方程近似为一阶惯性环节,其对应的状态空间方程式为

(8)

根据该空间状态方程,设计了拖拉机悬挂侧倾角的卡尔曼状态估计器.为了实际计算方便,对式(7)进行了离散化处理.经离散化后,状态估计器模型的状态方程和测量方程可描述如下:状态方程为

(9)

观测方程为

(10)

状态估计器在结构上分为时间更新和观测更新两部分.具体观测器设计步骤如下:时间更新部分为

(11)

(12)

式中:Pk,k为k时刻的误差协方差;Kk为卡尔曼滤波增益;Rk为离散化的观测噪声.

2 电控液压悬挂机构动力学模型

为了设计基于机具侧倾角预测的电控液压悬挂控制器,建立了某典型的具有侧倾自由度的电控液压悬挂系统动力学模型[7-9],如图2所示.

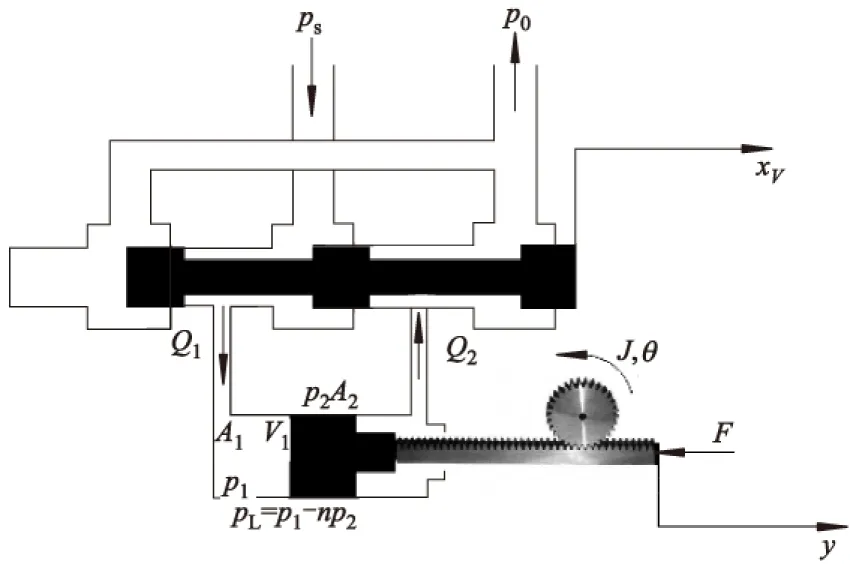
图2 液压系统动力学模型示意图

由于三位四通电磁阀左位与右位的液压系统动力学方程具有对称性,可仅考虑其右位流通的情况.

假设供油压力恒定,且回油缸压力为0 Pa,并且在实际耕作过程中阀芯位移较小,则阀的线性化流量方程可表示为

ΔqL=KqΔxv-KcΔPL,

(13)

式中:qL为负载流量,m3·s-1;Kq,Kc为电磁阀工作点的线性化系数;xv为液压阀移动位移,m;PL为负载压力,Pa.

由液压动力元件的流量连续性可得

(14)

式中:Ap为液压缸有效面积,m2;Vt为总压缩容积,m3;Ctp为液压缸总泄漏系数;βe为与液压回路特性有关的常数;dxp为齿条的位移变化量.

由于液压缸活塞杆用于驱动齿条,可得液压缸输出力与负载力的平衡方程为

(15)

式中:J为机具悬挂绕拖拉机坐标系x轴的转动惯量,kg·m2;r为驱动齿轮半径,m;xp为齿条的位移,m;F为作用在活塞上的外负载力,N.考虑到液压系统在耕作过程中的负载波动较小,文中假设负载F为一定值.

电控液压悬挂机构通过齿轮齿条实现直线运动与旋转运动间的转换关系,在实际耕作中,机具挂接装置与齿轮同轴安装,因此机具悬挂的旋转角度即为齿轮的旋转角度,由齿轮的运动学关系可得

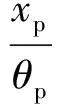
(16)

式中:θp为电控液压悬挂的实际侧倾角,rad.

通过联立式(13)-(16),经过Laplace变换后,可获得该典型电控液压悬挂的侧倾角与三位四通电磁阀阀体位移的传递函数为

(17)

式中：Kce为总流量-压力系数,且有Kce=Kc+Ctp.

3 模糊控制器设计

为了能够适应丘陵山地的复杂耕作环境,在保证横向耕作效果的同时降低控制器对于模型精确性的要求,文中根据上述建立的机具悬挂动力学模型设计了模糊控制器[10-11],并利用其对电控液压悬挂的侧倾角进行控制.

文中设计的模糊控制器包括2个输入与1个输出,为了方便模糊控制器进行控制,将输入与输出变量的值设定在区间[0,1],其输入变量分别为耕作坡地侧倾角预测信号与该坡地耕作侧倾角最大值的比值e以及耕作横向耕深波动与该处坡地侧倾角信号的比值ec.坡地侧倾角预测信号用于表征当前耕作坡地的实际坡度情况,横向耕深波动用于表征在某处坡地的实际耕作效果.输出变量为液压阀阀体实际位移与液压阀阀体最大位移的比值y,该变量用于实际控制液压阀的相关动作.

选定e的论域为[0,1],对应模糊集合为{S,M,B}，S,M,B分别表示小，中，大;ec的论域为[0,1],对应模糊集合为{SS,S,M,B,BB}，SS，S，M，B，BB分别表示较小,小,中,大,很大.y的论域为[0,1],对应模糊集合为{S,SM,BM,B}，S，SM，BM，B分别表示较小,中小,中大,大.上述变量的隶属度函数图线如图3-5所示.

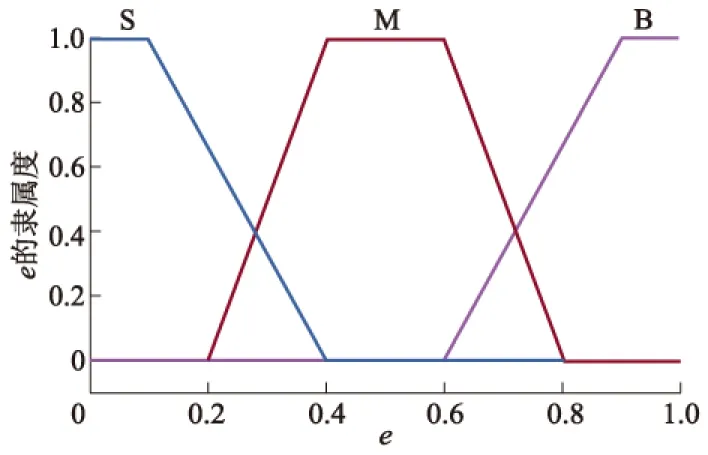
图3 e的隶属度函数图线

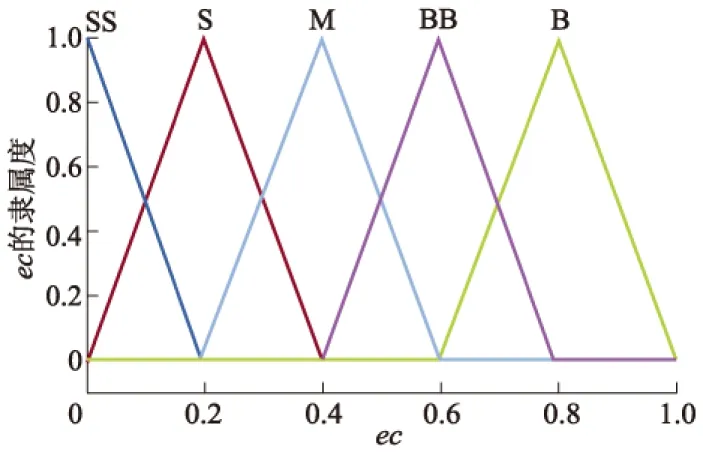
图4 ec的隶属度函数图线

图5 y的隶属度函数图线

为了能够获得较为优良的机具侧倾角控制效果,设计合理的模糊控制规则至关重要.当侧倾角预测信号较前值有较大变化或者具有较大横向耕作误差时,应当对电控液压悬挂实际侧倾角进行较大的调整.文中根据所建立的电控液压悬挂动力学模型设计了如表1所示的模糊控制规则,该控制规则所对应的模糊变量输入输出关系见图6.

表1 模糊控制规则表

图6 e，ec与y的关系

4 电液悬挂模型仿真及结果分析

为了验证该电控液压悬挂控制系统的有效性,在Matlab/Simulink中搭建了电控液压悬挂控制系统仿真模型,系统模型流程图如图7所示.

图7 电控液压悬挂控制系统模型流程图

文中的仿真工况为拖拉机以10 km·h-1匀速耕作,并在0 s时输入坡度为10°阶跃信号.耕作机具有效横向耕作宽度为1.2 m.电控液压悬挂进行仿真的主要参数如下:Ap=550 cm2,J=20 kg·m2,r=100 mm,βe=700 MPa,Ctp=0.2,Vt=220 cm2.

通过文中的传感器融合算法求解以及状态估计器估计，获得了电控液压悬挂侧倾角预测值、经过模糊控制器控制后的机具悬挂侧倾角实际值、使用与未使用电控液压悬挂控制系统的拖拉机横向耕深波动图线，如图8所示.

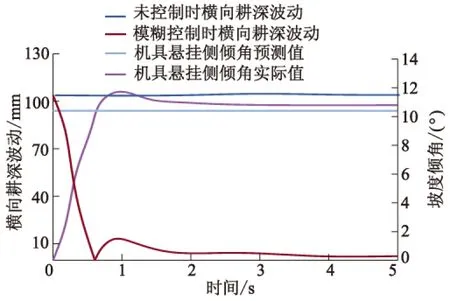
图8 阶跃坡度输入下机具仿真结果

从图8可见,采用传感器融合算法并结合机具悬挂状态估计器获得的机具悬挂侧倾角预测值从0 s发生阶跃.通过对比阶跃坡度输入下机具悬挂预测值与实际值的仿真图线可知,电控液压悬挂系统经过模糊控制器控制后,在1 s时信号发生超调后,其侧倾角很快收敛于预测值.

由图8中图线对比可见,在未有反馈控制的情况下,液压悬挂系统的横向耕深波动维持在10 mm,由于其横向耕深波动过大,对耕作质量影响较大.而利用模糊控制器控制的系统在经过0.5 s调整时间后,其横向耕深波动被控制在10 mm,最终电控液压悬挂的横向耕深波动的稳态误差趋于0 mm.据此可以看出,该控制系统能够有效保证横向耕作均匀性.

为了进一步说明该系统在实际耕作条件下对于横向耕深波动的控制效果,文中采集了实际耕作路面坡度信号,并将其作为模型输入信号进行系统仿真.实际采集的坡度信号波形如图9所示,仿真获得的横向耕深波动结果如图10所示.

图9 实际采集的坡度信号波形

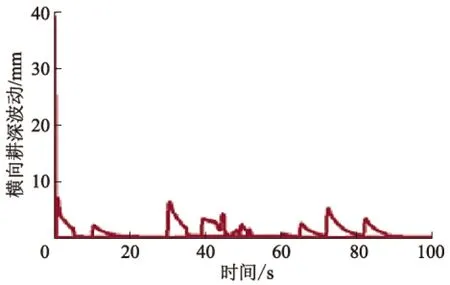
图10 试验数据信号输入下机具悬挂横向耕深波动图线

由图10可见,在实际信号输入条件下,该电控液压悬挂控制系统能够将机具悬挂横向耕深波动控制在10 mm以内,对于实际坡地耕作而言,该结果较为满意.

5 结 论

1) 文中利用在Matlab/Simulink中搭建的机具悬挂动力学控制模型进行了仿真,仿真结果表明,该反馈控制方案在10°坡度阶跃信号输入下,经过0.5 s即可将横向耕深波动控制在15 mm以内.在实际采集的路面谱信号输入下,该控制系统能够将横向耕深波动控制在10 mm以内,完全能够满足实际横向耕作均匀性要求.

2) 文中所提出的电控液压悬挂方案、电控液压悬挂动力学模型以及机具悬挂理想侧倾角状态估计模型完善了拖拉机机具悬挂横向倾角控制模型,为进一步改良自适应悬挂控制系统提供了有效保障.