有砟轨道结构刚度变化对既有线的影响研究
鹿 瑶
(重庆城市职业学院,重庆 402160)
0 引言
铁路作为最方便的出行方式之一,在交通领域拥有较高的地位,在国家的大力发展和支持下,我国铁路的发展位居世界前列,火车时速也在不断提高,旅客使用铁路安全、便捷、舒适、经济的出行要求也成了现在需要研究的目标。轨道是由多个构件复合形成的复杂结构,每部分的刚度都会影响整体结构的刚度。刚度作为一个重要参数不仅影响火车时速提升,还在轨道振动、变形以及安全、顺畅运行中起着关键作用。有砟轨道结构是我国快速铁路和普速铁路经常使用的结构形式,除此以外,还有福州至厦门、合肥至武汉、合肥至南京、宁波至温州、温州至福州、石家庄至太原等线路的高速铁路也应用了同样的结构[1]。在有砟轨道中,钢轨的种类决定了其弯曲刚度的数值;扣板、弹条以及钩头等零件的类型影响了每根钢轨紧固扣压件的刚度;有砟轨道与无砟轨道不同,其道床通常采用碎石等散粒体堆叠而成,碎石的种类、粒径大小以及堆叠厚度直接影响了铁路纵向的刚度值;路基作为铁路系统重要的支撑结构,其刚度因填料类型和密实度的改变,也会影响铁路纵向的刚度值。文章为了探究不同部分刚度的作用效果,拟从轨道动力学优化的角度,采用ANSYS Workbench建立仿真模型,通过控制不同部分的刚度变量,从静态响应和动态输出响应两方面研究其改变对既有线响应的影响规律。
1 分析方法
1.1 基本思路
用有限元方法作为主要手段,考虑轨道各部分应力以及每个部位在轨道中承担的作用,从有砟轨道结构的实际形式出发,使用分析软件ANSYS Workbench,构建将钢轨视为连续弹性离散点支承上的有限长梁的3层弹性点支承梁模型仿真模拟铁路结构[2],如图1所示。因为需要研究轨道刚度对响应的影响,故忽略弹性元件的阻尼。

图1 模型简化示意
1.2 整体轨道模型
为了充分考虑模拟的实际意义,模型使用目前国际上常用的数据。钢轨部分采用轨长25.0 m,轨矩1 435.0 mm的双轨仿真模拟。轨枕模型选取现阶段常用的Ⅲ型轨枕,轨枕的方向垂直于钢轨正线,相邻轨枕之间相距0.6 m。通过弹性元件模拟紧固扣压件将钢轨与轨枕联结起来。相邻道床之间相距0.6 m,与轨枕对照布置,通过弹性元件模拟道床弹性部分将轨枕与道床质量块元件连接起来。通过弹性元件模拟路基弹性部分将道床质量元件连接到基础上。
2 分析过程
2.1 静力学方面
我国电力机车车辆的设计轴重为25 t,在每个车辆的一个转向架上,两对相互平行的轮对能产生4个两两平行、间距为2 500 mm、大小为125 kN的竖向静荷载。
仿真14种不同情况,每种情况都采用不同的钢轨抗弯刚度以及扣件、道床和路基刚度,模拟既有线中刚度的改变。由于每种情况中各部分刚度不同,会使轨道结构在静力荷载作用下产生的应力以及沿Z方向产生的纵向位移发生不同的变化,因此,有必要利用折线图汇总轨道结构整体、单轨、轨枕、道床静态响应的变化情况,以分析其变化规律[3]。轨道系统控制变量如表1所示。未列出的钢轨抗弯刚度利用60 kg/m和75 kg/m钢轨不同的断面尺寸进行改变。

表1 轨道系统控制变量
2.2 动力学方面
在火车运行过程中,同一段轨道不断受到轮对的作用,所以模型在对动力学方面进行分析时,需要利用周期性荷载模拟轨道受到的动力荷载,其大小以及间距都应与静力荷载相同。有砟轨道常用的道砟和路基是散粒体堆叠形成的,这些颗粒之间接触的频繁程度主要由轨道所受荷载的频率所决定。首先,要保证加荷频率不能过小,否则支撑在道砟之上的道床随着加荷频率变大,产生的最大接触力也会变大。其次,需要设定加荷频率的上限值,否则当加荷频率不断趋近至超过轮轨系统的同相共振频率时,很大概率会激化整个轨道的高频振动,还会在轨枕上引发反相振动。在模型上施加正弦稳幅荷载,其频率为10 Hz,幅值为125 kN。除了加载频率外,加载周期也是需要考虑的影响因素,通过多次仿真对比后发现,加载1.5个周期后动态响应变化产生了稳定的规律,因此,加载周期选择1.5个。需要注意的是,分析过程中需要约束模型的X,Y方向。
动力学方面分析方法与静力学类似,利用折线图汇总轨道结构整体、单轨、轨枕、道床在周期性荷载作用下产生响应的变化情况,以便分析其变化规律。与静力学分析时不同的是,周期荷载作用下每段钢轨不同时刻的应力和位移都不同,因此,有必要选择在静载下单轨、轨枕和道床上产生最大应力及最大位移的危险点作为分析钢轨、轨枕和道床变化规律的点。同理,在周期性载荷的作用下,轨道结构产生的最大等效应力和最大纵向位移也将显示周期性变化,因此,将最大等效应力和最大纵向位移的周期性变化进行比较更加符合实际。相对的,轨道结构的加速度并不会产生周期性的变化,因此,在分析加速度的变化趋势时选取某一时刻最大值的变化进行比较更有意义。
3 轨道刚度对既有线响应的影响
通过仿真轨道刚度对既有线响应的影响刚度对既有线响应的影响可以得出以下结论:
(1)钢轨抗弯刚度对有砟轨道结构静力响应影响较小,但对其动力响应有显著影响。在钢轨抗弯刚度变大的同时,其动力响应,如最大等效应力、最大动位移都会变小。与此相反的是结构整体、钢轨危险点、轨枕和道床加速度的最大值会变大。
(2)扣件刚度对有砟轨道结构静力响应有一定影响,在其刚度变大时,轨枕、道床的最大应力和最大位移都会变大。轨枕和道床的动力响应也会产生相同的变化,其最大等效应力、最大动位移以及加速度的最大值都随扣件刚度的变大而增大。
(3)道床刚度变大时,有砟轨道轨枕和道床的静力响应都会变大。轨枕和道床在周期性动荷载作用下产生的最大应力都随着道床刚度的变大而增大,轨枕和道床加速度的最大值随着道床刚度的变大而减小。轨枕在周期性动荷载作用下产生的最大动位移随着道床刚度的变大而减小,道床的最大动位移则增大。
(4)路基刚度变大时,轨枕以及道床的最大应力会变大,结构整体、钢轨、轨枕和道床的最大位移会变小。结构整体、钢轨、轨枕和道床的动力响应也会受到路基刚度的影响。路基刚度变大的同时,轨枕和道床产生的最大等效应力都变大,结构整体、钢轨危险点、轨枕和道床的最大动位移有变小的趋势,与此相反的是钢轨危险点、轨枕和道床加速度的最大值变大。
4 轨道刚度匹配
通过仿真模拟的结果可以发现,钢轨抗弯刚度以及扣件、道床、路基刚度都会对有砟轨道结构的响应产生影响,其中后3项对轨道各部分的动力响应影响较大。对于既有线路而言,路基刚度改变起来比较困难,所以可以通过改变扣件、道床刚度,来控制轨道的响应。使两者的比例在0.250 0和1.333 3之间不断改变,绘制静态最大应力和动态最大应力的变化曲线,获得最优刚度比。
从图2的曲线可以发现,两者比例变化对整体和单轨静态的最大应力几乎没有作用。轨枕和道床的最大应力变化曲线出现谷值,所以选择其对应的横坐标0.5作为最优刚度比。从图3的曲线可以发现,单枕和道床的动应力变化曲线谷值对应的横坐标也是0.5,所以0.5作为最优刚度比也满足了动力响应的要求。

图2 静态最大应力变化曲线
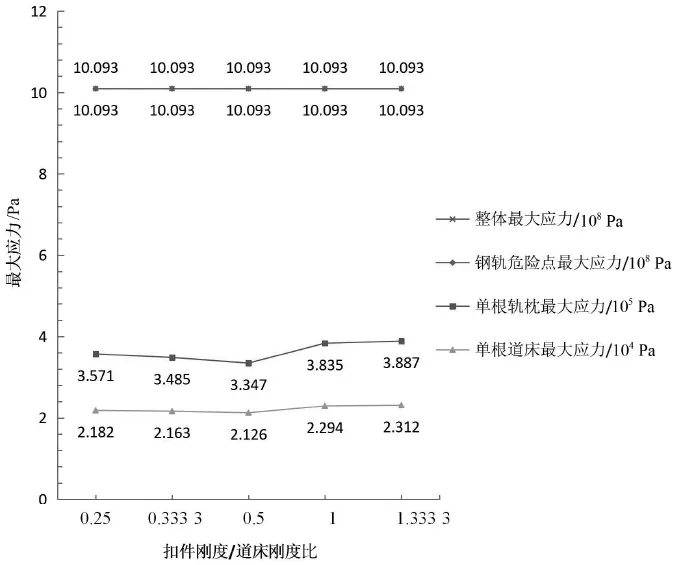
图3 动态最大应力变化曲线
5 轨道总刚度动力学优化
通过仿真数据可以得出结论,轨道总刚度和动力响应成正比例变化。确定扣件及道床刚度最优的比例后,可以通过将轨道总刚度控制在一定的范围内变化,保证铁路结构的动力响应更小,实现对轨道总刚度的动力优化。因此,对轨道总刚度的动力学优化可以转换为求解在一定范围内轨道总刚度的最小值。为了求解这个有效的变化范围,需要通过限定和约束铁路结构整体应力和应变的大小来计算轨道总刚度的最大值和最小值。
5.1 轨道总刚度的最小值
轨道总刚度的最小值是在确定扣件及道床刚度最优的比例后,利用等效钢度的公式进行计算。在求解过程中,先选取能够保证最优刚度比时,轨道结构中紧固扣压件、道床和路基的刚度值代入下式,求得轨下基础半枕支承的整体刚度:

式中,kz——半枕支承的整体刚度;
kr——扣件的刚度;
ks——轨下半枕道床支承刚度;
kb——轨下半枕路基支承刚度。
将枕间距离a代入,可以求得单轨的连续支承刚度为:

利用连续弹性支承轨道静力计算公式,可以计算出轨道等效钢度,即轨道总刚度的最小值为:

式中,E——钢轨弹性模量;J——钢轨截面惯性矩。
当有砟轨道结构采用扣件及道床刚度最优的比例0.5时,匹配的道床、路基和扣件的刚度分别为80 kN/mm、80 kN/mm和40 kN/mm。经过上述求解过程,得出所求范围的最小值为62.943 kN/mm。
5.2 轨道总刚度的最大值
在计算轨道总刚度的最大值时,如果把刚度整体简化为一个弹性结构,那么利用加载在轨道结构整体上的荷载除以整体最大的动位移,得到的就是轨道总刚度的最大值。
在仿真模拟过程中,加载在轨道结构上的荷载大小为125 kN,选取轨道结构紧固扣压件及道床刚度最优的比例0.5时,结构整体动位移的最大值为1.162 1 mm。经过上述求解过程,得出所求范围的最大值为107.56 kN/mm。
6 结语
(1)有砟轨道结构在静态荷载和周期性动力荷载作用下,轨道各部分刚度改变对既有线路的影响具有一定的规律性,可以通过增加轨道结构各部分刚度,减小有砟轨道结构整体的响应。但要注意其变化对钢轨、轨枕以及道床响应的影响,应考虑轨道总刚度的变化界限。
(2)通过改变扣件、道床刚度,可以控制轨道的响应。两者的比列为0.5时,轨枕和道床的最大静应力和动应力的曲线均出现谷值,所以选择0.5作为有砟轨道结构的最优刚度比。经过动力学优化后得到有砟轨道结构总刚度合理选取范围为62.943~107.56 kN/mm。

