针轮输出摆线钢球传动减速器的设计与研究
鲍君华,阮 超,何卫东
(大连交通大学机械工程学院,辽宁 大连 116028)
0 引言
摆线针轮行星传动具有一系列重要优点,包括多齿啮合和齿面硬化、体积小、重量轻、传动比范围广、传动平稳、效率高、噪音低等,因此它得到广泛的应用并且占据了大部分的减速机产品市场。利用包括多齿啮合和硬化齿面的优点,摆线轮的承载能力很强,但在传统驱动中没有得到充分应用,因此,减速器的承载能力有限。作为输出轴,输出机构通常采用的结构方式为悬臂梁式,不仅降低了输出轴的刚度,而且无法精确保证所要求的回转精度。通过改进设计和结构优化形成的针轮输出摆线钢球传动减速器在一定程度上克服了以上缺点[1],针轮输出摆线钢球传动是一种特殊形式的行星齿轮传动,其利用钢球作为中间构件,在摆线轮和针齿壳构成的滚道内作啮合运动[2]。具有如下优点:
(1)针轮输出摆线钢球传动减速器与传统摆线针轮减速器相比,在体积和重量不翻倍的情况下,输出转矩和功率可以翻倍。因此,每单位质量的功率将增加并且产品的成本降低。输出轴结构由原先的悬臂梁改进为简支梁结构,提高了受力条件及输出轴的刚度和回转精度,同时,整机的结构更加简单、拆装方便、制造简便。
(2)采用曲面摆线齿型可以降低摆线轮和钢球在接触面上接触应力的大小,进一步利用多齿内啮合的针摆行星传动的优点,提高整机的承载能力或在承载能力不变的前提下减小结构尺寸。
(3)现有的摆线轮与针齿之间接触方式为直线接触,存在齿向偏载的现象,限制其承载能力,因此,将针齿改进为钢球,同时,为了实现摆线轮与钢球的最佳曲线接触关系,将摆线轮设计为一种内凹的球面包络曲面摆线齿形,实现了摆线轮与针齿之间的曲线接触,提高了承载能力。与传统结构点接触相比较,本结构则具有更好的传动受力效果和更高的传动效率。
1 针轮输出减速器工作原理及结构
针轮输出摆线钢球传动减速器的工作原理如图1所示。4片结构和尺寸均相同的摆线轮7作为行星运动的行星轮装入到输入轴端的输入轴3上,数量为8的柱销8既穿过4片摆线轮上的柱销孔又固定连于减速箱体上。当摆线轮受输入轴驱动转动时,摆线轮中心不仅会围绕针齿壳中心进行公转,而且在与钢球啮合作用下会进行自转。但由于受到柱销的约束限制了摆线轮自身的角速度,从而得到摆线轮的自转转速为0,因此,实际上摆线轮只能在垂直于柱销所在的平面做平面平动。在作平面平动过程中,摆线轮与钢球啮合传动完成针摆行星传动,再通过钢球与针齿壳啮合运动将动力输出到输出轴。
根据行星齿轮系传动设计的计算方法[3],可得到数。为了安装适应4个摆线齿轮的结构,提高输出轴和柱销的刚度和强度,考虑到结构的改进和优化,设计减速器的具体结构如图1所示。减速器的主要特点就是输入轴通过图1中部件4的中心孔插入减速器的内部,并支撑在一对转臂轴承上。两个偏心套筒组装在输入轴上,转臂轴承组装在偏心套筒上,4片摆线轮安装在两个错位180°的转臂轴承上。考虑到摆线轮和偏心套筒间的摩擦,则将滚动轴承装于它们之间,同时考虑到径向安装空间,滚动轴承往往都不带外圈,而直接以摆线轮的中心孔表面直接作为滚道。由于在工作时转臂轴承所受到的力往往很大,而且转速较高,故为保证转臂轴承的使用寿命,文章采用整体偏心转臂轴承。摆线轮齿通过输入轴驱动行星运动,同时,齿轮上的输出轴端箱盖与箱盖固定,并固定在地面上,然后摆线轮与柱销啮合并且与针齿壳上的钢球啮合,因此,钢球可以旋转并输出运动和扭矩。输入轴、输出轴和柱销可以简单理解为简支梁结构,提高了减速器的刚性和承载能力。

图1 针轮输出摆线钢球传动减速器结构
2 参数设计
根据经典的摆线行星44传动的参数设计和计算方法,再结合视觉基础(Visual Basic,VB)软件编制出参数化系统。通过分析计算使用该软件将新型驱动原型的参数列于表1中。根据减速器传动比的选择原则,选择一齿差作为摆线轮的结构,因此,钢球的个数等于传动比。
根据表1中列出的基本参数,可以得出摆线齿轮的结构基本参数,为减速器的强度校核和计算提供依据。根据减速器工作时柱销的变形及柱销与齿轮间的原始间隙的关系,通过分析变形的相容性的条件,可以计算出工作齿数及其接触力。根据力矩平衡条件将公式整理如下:

式中:Li是每个摆线轮齿啮合力力臂;m,n是轮齿受力的起始编号和终止编号;δi是每个轮齿的弹性
理论上,针摆行星传动的接触齿数是摆线轮齿数的一半。齿轮接触的齿数越多,工作状况越不好,摆线齿轮应采用改进后的齿形,接触齿数少于齿轮齿数的一半,以达到理想的啮合工作状态和高传动效率为目的选择接触齿数。应用表1中列出的原始计算数据进行强度校核,文章中的计算方法与传统计算方法存在差异,采用分层计算求和的计算方法。图2为力分析的界面和各齿的受力情况及摆线轮的接触应力计算值。由结果可知,初始间隙和变形量两栏采用上述方法可得出多组分层数据,可归纳为摆线轮有12个齿接触受力,最大受力齿出现在齿数9处,力约为22.14 N。齿轮作用于齿轮节点的等效径向力约为11.27 N,切向力约为202.07 N,啮合合力约为202.38 N,与合力方向角为3.19°,从图中还可以得出摆线轮的计算应力值为1 082.26 MPa,小于材料许用接触应力值,计算结果反映了良好的受力状态。

表1 针轮输出摆线钢球传动减速器的基本参数
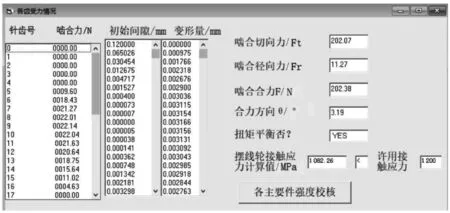
图2 摆线齿轮的受力分析结果
3 摆线轮参数化建模
摆线轮是减速器上一个非常重要的零部件,摆线轮模型建立的准确性对接触应力分析的准确性十分关键。根据摆线齿廓曲线的形成原理,建立通用的摆线轮齿形方程式,在创立方程式的过程中,以摆线轮几何中心oc作为坐标系原点,通过oc且与摆线轮齿槽对称轴重合的轴线作为xc轴,则可建立通用的摆线轮齿形方程式。
在Creo软件中,利用“基准→曲线→来自方程的曲线”的指令建立摆线轮齿廓在笛卡尔坐标系下的方程式。而在本文中创建的齿廓方程式采用的是切割分层的思想,该思想中的切割分层的半径是一系列垂直于摆线轮轴线并与钢球球体相割后获得的相交圆的半径值,本文中取 z1=0,z1=±1,z1=±1.5,z1=±2,z1=±2.9共9个数值(单位为mm),进行切割分层,由表1可知,钢球半径rrp0=4 mm,可根据勾股定理将切割分值,同理每次切割分层所求的rrp值共9组再代入到通用的摆线轮齿形方程中即可生摆线齿廓曲线,具体的摆线轮齿廓曲线方程如图3所示,图3只单列出z1=0的一种情况,其他8种情况参考图3一一建立列出。
摆线轮齿廓曲线创建完成后,通过混合命令中的选取截面指令从前往后逐一选取曲线即可生成摆线轮齿槽啮合摆线轮模型,再选1取图4中z=(±2.9)mm所在曲线方程投影拉伸1.5 mm即可生成摆线轮齿坯模型,然后根据朱孝录[4]设计的手册可计算出柱销孔的数量和摆线轮上柱销孔圆的直径以及中心孔圆的直径,通过拉伸切除命令可得到对应的中心孔圆及柱销孔圆。拉伸切除命令创建完成后即得到摆线轮实体模型,如图4所示。

图3 摆线轮齿廓曲线方程

图4 摆线轮三维实体模型
摆线轮实体模型创建完成后,为了能对现有虚拟样机进行改进,在Creo中建立了一种新的减速器模型结构,同时对零件进行了干涉检查,无干涉现象。
4 有限元接触分析
4.1 网格的划分
在上节建立好的三维模型的基础上利用ANSYS Workbench与Creo中的接口将三维模型导入Workbench中,将上述建立好的模型保存成stp格式,然后导入到Workbench中进行有限元分析[5-8]。为保证分析计算准确,需要对模型进行整体的网格划分,为了能够得到更加平滑的网格质量,需选择transition指令框中slow选项,网格划分后如图5所示。

图5 摆线针轮啮合有限元模型
4.2 接触对和材料属性
在导入配合好的三维模型后,ANSYS Workbench会自动识别接触。如果凸的表面和平面或凹面接触,应该选取平面或凹面为目标面,则摆线轮为目标面,钢球为接触面[8]。本次分析中的摆线轮、钢球、针齿壳和柱销均采用GCr15,在进行分析之前,需要设置摆线轮本身的一些属性,如:弹性模量取2.1×1011Pa,泊松比取0.3,密度取7900kg/m3等。
4.3 边界条件的施加与载荷
4.3.1 定义边界条件
在本次的分析中,模型中摆线轮与钢球的啮合传动及摆线轮与柱销的啮合传动的接触类型为摩擦接触,设定摩擦系数为0.1,采用的算法为增广拉格朗日算法,对柱销两端施加固定约束,在针齿壳的外表面施加圆柱约束,限制轴向、径向的自由度,只保留其绕中心轴转动的自由度。
4.3.2 定义载荷
(1)计算减速器的总输出转矩:

=56 584 N·mm
(2)计算单片摆线轮传递转矩:
文章中减速器共有4片摆线轮,考虑到制造及安装的误差,4片摆线轮传递的转矩并不是相等的,即单片摆线轮上所传递的转矩值Tc应略大于1 4T,所以在进行力分析与强度计算时,建议Tc可取0.275 T。
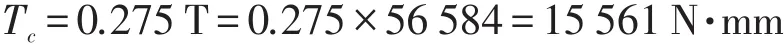
在文章中载荷需加在针齿壳的外表面处,大小为Tc与针齿壳的外表面以及表面半径的比值。
4.4 有限元分析结果
图6求解结果为摆线轮的等效应力的分析结果,最大等效应力为970.88 MPa。可以看出摆线轮在啮合力的作用下的受力变形,摆线轮辐发生了较大的弹性变形,图7为在该处啮合时摆线轮齿的啮合接触斑,最大接触应力为1 015.6 MPa,且等效应力集中在钢球与摆线轮相互啮合的接触位置,应力分布形状接近于椭圆,应力值以最大应力值为中心逐渐向四周降低,没有出现应力集中的现象。通过分析比较摆线轮及钢球受力均满足要求,并具有较大的承载能力余量,摆线轮齿与钢球的接触斑主要位于摆线轮轮齿及钢球的接触位置,接触良好[8]。
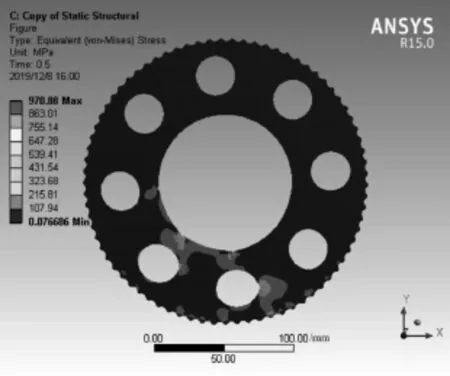
图6 摆线轮等效应力

图7 摆线轮齿面接触斑
5 结语
(1)文章分析了新型摆线针轮传动的工作原理,并结合VB软件编制出参数化系统,对这种传动在合理的范围内进行参数的设计计算和具体结构尺寸的确定,通过Creo三维建模软件建立了整机的三维实体模型,获得了较完整的设计计算理论和参数化建模方法,为实物样机的制造提供了理论基础。
(2)结合三维建模、有限元接触分析计算方法,通过计算机分析计算,对摆线轮传动有限元装配模型施加边界条件,并进行静力学分析的求解,通过分析求得摆线轮及钢球啮合的应力接触斑分布情况及摆线轮的等效应力值。由计算机分析软件分析得出,摆线轮的计算应力值为1 082.26 MPa,有限元仿真所得到的最大接触应力值为1 015.60 MPa,误差仅为6%,满足精度要求。

